ОДНООСНЫЕ — это… Что такое ОДНООСНЫЕ?
ОДНООСНЫЕ КРИСТАЛЛЫ — кристаллы, для которых характерно двойное лучепреломление света при всех направлениях падающего луча, кроме одного направления, называемого оптической осью кристалла … Большой Энциклопедический словарь
ОДНООСНЫЕ КРИСТАЛЛЫ — кристаллы, в к рых происходит двойное лучепреломление при всех направлениях падающего на них луча света, кроме одного, наз. оптической осью кристалла. (см. КРИСТАЛЛООПТИКА). Физический энциклопедический словарь. М.: Советская энциклопедия.… … Физическая энциклопедия
одноосные кристаллы — кристаллы, для которых характерно двойное лучепреломление света при всех направлениях падающего луча, кроме одного направления, называемого оптической осью кристалла. * * * ОДНООСНЫЕ КРИСТАЛЛЫ ОДНООСНЫЕ КРИСТАЛЛЫ, кристаллы, для которых… … Энциклопедический словарь
Одноосные кристаллы — кристаллы, для которых характерно Двойное лучепреломление при всех направлениях падающего на них света, кроме одного (это направление называется оптической осью кристалла).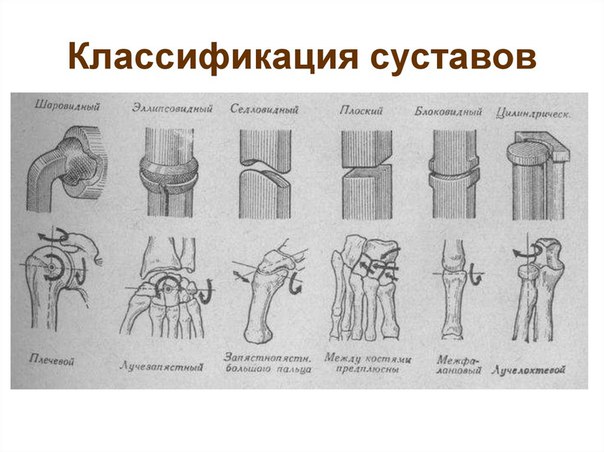
ОДНООСНЫЕ КРИСТАЛЛЫ — кристаллы, для к рых характерно двойное лучепреломление света при всех направлениях падающего луча, кроме одного направления, называемого оптич. осью кристалла … Естествознание. Энциклопедический словарь
ОДНООСНЫЕ РАСТЕНИЯ — растения, у которых главная ось органов возобновления завершается формированием терминального цветка … Словарь ботанических терминов
ТЕЛЕЖКИ ЛОКОМОТИВНЫЕ ОДНООСНЫЕ — выполняются обычно в форме тележки Бисселя с точкой поворота, расположенной за осью. Рама тележки снабжается водил ом 2, либо являющимся ее продолжением в виде треугольника, либо выполняемым в форме стальных полос, образующих треугольник и… … Технический железнодорожный словарь
Геосетка — Геосетка плоский полимерный рулонный материал с сетчатой структурой, образованный эластичными ребрами из высокопрочных пучков нитей, скрепленными в узлах прошивочной нитью, переплетением, склеиванием, сплавлением или иным способом, с… … Википедия
Закладка — Закладка, закладной элемент вид альпинистского снаряжения, предназначенный для организации страховки на скалах. Условно закладки можно разделить на два класса: закладки с неизменяемой геометрией; закладки с изменяемой геометрией. Работа… … Энциклопедия туриста
Условно закладки можно разделить на два класса: закладки с неизменяемой геометрией; закладки с изменяемой геометрией. Работа… … Энциклопедия туриста
Кремнероговые губки — (Cornacuspongida) самый большой отряд губок. Скелет состоит из одноосных кремнёвых игл (рис.) и органического вещества спонгина, или только из спонгиновых волокон. Канальная система лейконоидного типа. К. г. большей частью образуют… … Большая советская энциклопедия
одноосный — это… Что такое одноосный?
одноосный — одноосный … Орфографический словарь-справочник
одноосный — прил., кол во синонимов: 1 • одноостный (2) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
одноосный — одноосный, одноосная, одноосное, одноосные, одноосного, одноосной, одноосного, одноосных, одноосному, одноосной, одноосному, одноосным, одноосный, одноосную, одноосное, одноосные, одноосного, одноосную, одноосное, одноосных, одноосным, одноосной … Формы слов
одноосный — одно осный … Русский орфографический словарь
одноосный — одноо/сный … Слитно.
одноосный — ая, ое. С одной осью. О. автомобиль, автоприцеп … Энциклопедический словарь
одноосный — ая, ое. С одной осью. Одноо/сный автомобиль, автоприцеп … Словарь многих выражений
одноосный — одн/о/ос/н/ый … Морфемно-орфографический словарь
одноосный (оптическая ось) кристалл — — [Англо русский геммологический словарь. Красноярск, КрасБерри. 2007.] Тематики геммология и ювелирное производство EN uniaxial … Справочник технического переводчика
одноосный дорожный каток — Примечание. В соответствии с числом осей дорожному катку присваивается наименование двухосный, трехосный дорожный каток [ГОСТ 21994 82] Тематики строит. машины, оборуд., инструмент прочие … Справочник технического переводчика
одноосный кристалл — Кристалл, имеющий только одну оптическую ось.
Прицепы и полуприцепы для автомобилей и тракторов | ||
Прицепы к легковым автомобилям и автобусам | ||
Прицепы к легковым автомобилям всех видов | ||
Прицепы к автобусам | ||
Прицепы служебные | ||
Прицепы для перевозки людей | ||
Прицепы одноосные к грузовым автомобилям и шасси | ||
Прицепы одноосные с бортовой платформой | ||
Прицепы одноосные роспуски | ||
Прицепы одноосные самосвальные | ||
Прицепы одноосные фургоны | ||
Прицепы одноосные специальные | ||
Прицепы одноосные шасси | ||
Прицепы одноосные прочие | ||
Прицепы двухосные к грузовым автомобилям | ||
Прицепы двухосные с бортовой платформой | ||
Прицепы двухосные роспуски | ||
Прицепы двухосные самосвальные | ||
Прицепы двухосные шасси | ||
Прицепы двухосные прочие | ||
Прицепы тракторные | ||
Прицепы тракторные одноосные | ||
Прицепы тракторные двухосные | ||
Прицепы тракторные бортовые | ||
Прицепы тракторные шасси | ||
Прицепы тракторные прочие | ||
Прицепы со специализированными кузовами, трейлеры | ||
Прицепы со специализированными кузовами | ||
Прицепы для ветеринарной службы | ||
Трейлеры и специальные тяжеловозные прицепы и полуприцепы | ||
Опоровозы на полуприцепах | ||
Прицепы — цистерны для перевозки нефтепродуктов и воды (цистерны для нефтепродуктов, воды и сжиженных газов на прицепах и полуприцепах) | ||
Прицепы — цистерны для нефтепродуктов | ||
Полуприцепы — цистерны для нефтепродуктов | ||
Топливозаправщики, маслозаправщики и водозаправщики на прицепах и полуприцепах | ||
Цистерны для сжиженных газов на прицепах и полуприцепах | ||
Цистерны для воды на прицепах | ||
Цистерны для воды на полуприцепах | ||
Прицепы — цистерны прочие | ||
Полуприцепы автомобильные общего назначения | ||
Полуприцепы автомобильные общего назначения с бортовой платформой | ||
Полуприцепы автомобильные общего назначения самосвальные | ||
Полуприцепы автомобильные общего назначения со специализированными кузовами | ||
Полуприцепы автомобильные общего назначения. | ||
Полуприцепы автомобильные общего назначения прочие | ||
Полуприцепы автомобильные для строительных конструкций | ||
Настиловозы, фермовозы, балковозы, плитовозы и металловозы | ||
Полуприцепы для перевозки строительных конструкций прочих |
67315-17: СОА Стенды одноосные автоматизированные
Назначение
Стенды одноосные автоматизированные СОА (далее по тексту — стенды) предназначены для воспроизведений и измерений угловой скорости и углового перемещения.
Описание
Принцип действия стенда основан на преобразовании вращения вала двигателя в прецизионное угловое перемещение поворотной платформы стенда с заданной скоростью.
Стенд представляет собой оптико-механический аппаратно-программный комплекс и состоит из электромеханической системы и блока электроники.
Электромеханическая система представляет собой поворотную платформу, на оси вращения которой расположены датчик угла и серводвигатель.
Блок электроники включает в себя систему управления двигателями, блок питания и компьютер.
Стенды СОА выпускаются в двух модификациях: СОА-15 и СОА-2, которые отличаются грузоподъёмностью, диапазоном и погрешностью измерений угловой скорости и углового перемещения.
Общий вид стенда, схема пломбировки от несанкционированного доступа и место нанесения знака поверки представлены на рисунке 1.
Программное обеспечение
Программное обеспечение (ПО) является встроенным и функционирует на компьютере под управлением операционной системы Microsoft Windows XP/Vista/7.
Программное обеспечение реализует функциональность стенда и обеспечивает выполнение следующих функций:
— воспроизведение и отображение значений угловой скорости;
— измерение и отображение результатов измерений углового положения.
ПО устанавливается на предприятии-изготовителе и недоступно для изменений вне заводских условий без использования специального оборудования производителя.
Влияние программного обеспечения на метрологические характеристики учтено при нормировании метрологических характеристик.
Уровень защиты ПО от непреднамеренных и преднамеренных изменений соответствует уровню «Средний» по Р 50.2.077-2014.
Идентификационные данные программного обеспечения приведены в таблице 1.
Таблица 1 — Идентификационные данные программного обеспечения стенда
|
Идентификационные данные (признаки) |
Значения |
|
Идентификационное наименование ПО |
StendControl |
|
Номер версии (идентификационный номер) ПО |
2.0 и выше |
|
Цифровой идентификатор (контрольной суммы исполняемого кода) ПО |
35B2C1, CRC32 |
|
Примечание: значение контрольной суммы приведено для версии 2. | |
Технические характеристики
Таблица 2 — Метрологический характеристики
|
Наименование характеристики |
Значение | |
|
СОА-2 |
СОА-15 | |
|
Диапазон воспроизведений угловой скорости, °/с |
±720 |
±1500 |
|
Диапазон измерений углового перемещения, градус |
±360 | |
|
Пределы допускаемой относительной погрешности воспроизведений угловой скорости при измерении на угле 360°, % — для угловой скорости от 0,01 до 0,1 включ. °/с — для угловой скорости св. 0,1 °/с |
±0,05 ±0,02 |
±0,1 ±0,05 |
|
Пределы допускаемой абсолютной погрешности измерений углового перемещения, секунда |
±2,5 |
±15 |
|
Наименование характеристики |
Значение | |
|
СОА-2 |
СОА-15 | |
|
Параметры электропитания: | ||
|
— напряжение переменного тока, В |
230±23 | |
|
— частота переменного тока, Гц |
50±1 | |
| Потребляемая мощность, кВ А, не более |
5 |
1,5 |
|
Условия эксплуатации: | ||
|
— температура окружающей среды, °С |
от +10 до +35 | |
|
— относительная влажность воздуха, %, не более |
85 | |
|
Масса, кг, не более | ||
|
— электромеханическая система |
100 |
50 |
|
— блок электроники |
20 |
10 |
|
Г абаритные размеры, мм, не более | ||
|
— электромеханическая система | ||
|
— диаметр |
500 |
500 |
|
— высота |
500 |
400 |
|
— блок электроники | ||
|
— длина |
500 |
500 |
|
— ширина |
500 |
500 |
|
— высота |
700 |
700 |
|
Г рузоподъёмность стенда, кг, не более |
50 |
30 |
|
Средний срок службы, лет |
10 | |
|
Средняя наработка до отказа, ч |
10000 | |
Знак утверждения типа
наносится на информационную табличку электромеханической системы фотохимическим методом и на титульные листы паспорта и руководства по эксплуатации типографским способом.
Комплектность
Таблица 4 — Комплектность средства измерений
|
Наименование |
Обозначение |
Количество |
|
Электромеханическая система |
1 шт. | |
|
Блок электроники |
1 шт. | |
|
Комплект соединительных кабелей |
1 шт. | |
|
Руководство по эксплуатации |
СОА.001.РЭ |
1 экз. |
|
Паспорт |
СОА.001.ПС |
1 экз. |
|
Методика поверки |
МП 253-009-2017 |
1 экз. |
Поверка
осуществляется по документу МП 253-009-2017 «Стенды одноосные автоматизированные СОА. Методика поверки», утверждённому ФГУП «ВНИИМ им. Д. И. Менделеева» 25. 01.2017 г. Основные средства поверки:
01.2017 г. Основные средства поверки:
— призмы правильные многогранные ППМ, рег. № 62371-15;
— частотомер электронно-счётный Ч3-85/3, рег. № 32359-06;
— автоколлиматоры цифровые TriAngle TA и TriAngle TA HS, рег. № 47437-11. Допускается применение аналогичных средств поверки, обеспечивающих определение
метрологических характеристик поверяемых СИ с требуемой точностью.
Знак поверки наносится на информационную табличку блока электроники.
Сведения о методах измерений
приведены в эксплуатационном документе.
Нормативные документы
СОА.001.ТУ Стенды одноосные автоматизированные СОА. Технические условия
Код ТН ВЭД 8701100000. Тракторы одноосные. Товарная номенклатура внешнеэкономической деятельности ЕАЭС
Позиция ТН ВЭД
|
Позиция ОКПД 2
Таможенные сборы — ИМПОРТ
| Базовая ставка таможенной пошлины | 10% реш.  54 54 |
| Акциз | Не облагается |
| НДС | 20% |
Рассчитать контракт
Одноосные и двуосные кристаллы — Энциклопедия по машиностроению XXL
Напоминаем, что мы описываем явления, происходящие в кристалле исландского шпата. Они типичны для большой группы кристаллов, обладающих одной оптической осью и носящих название одноосных. Сложнее обстоит дело в так называемых двуосных кристаллах, где ни один из лучей нельзя назвать обыкновенным. Во многих одноосных и двуосных кристаллах поглощение обеих распространяющихся в кристалле световых волн различно. Типичным представителем такого кристалла является турмалин, в котором обыкновенный луч практически полностью поглощается уже при толщине около 1 мм (см. 108).
[c.383]
Они типичны для большой группы кристаллов, обладающих одной оптической осью и носящих название одноосных. Сложнее обстоит дело в так называемых двуосных кристаллах, где ни один из лучей нельзя назвать обыкновенным. Во многих одноосных и двуосных кристаллах поглощение обеих распространяющихся в кристалле световых волн различно. Типичным представителем такого кристалла является турмалин, в котором обыкновенный луч практически полностью поглощается уже при толщине около 1 мм (см. 108).
[c.383]
Одноосные и двуосные кристаллы [c.506]
По правилу Френеля сечение эллипсоида, перпендикулярное оптической оси кристалла, должно характеризоваться равенством полуосей, т. е. это сечение должно иметь форму круга, а оптическая ось кристалла является его осью симметрии. Это правило объясняет, что в природе встречаются только одноосные и двуосные кристаллы, так как эллипсоид не может иметь более двух круговых сечений, расположенных симметрично относительно его главных осей. Если оба круговых сечения сливаются, то кристалл оказывается одноосным и 81 — 8о = 8. Этот случай
[c.196]
Если оба круговых сечения сливаются, то кристалл оказывается одноосным и 81 — 8о = 8. Этот случай
[c.196]
Различие между одноосными и двуосными кристаллами становится особенно очевидным, если рассмотреть поверхность волновых векторов к (т. е. геометрическое место точек концов к-вектора как функцию направления). Поскольку любой анизотропный кристалл имеет два показателя преломления для двух взаимно перпендикулярных направлений поляризации, волновые векторы всегда образуют две поверхности. В случае одноосного кристалла одна из поверхностей, соответствующая обыкновенной волне, является сферой. Другая поверхность есть эллипсоид вращения. Пересечение этой поверхности с плоскостью рассматривалось в разд. 1.5. Заметим еще раз, что эта поверхность не является оптической индикатрисой. Например, для положительного одноосного кристалла ось z оптической индикатрисы является большей осью, в то время как для поверхности волнового вектора ось z является меньшей осью.
[c. 35]
35]
Наряду с одноосными кристаллами в этой главе кратко рассмотрены и двуосные кристаллы — согласование фазовых скоростей обладает в них рядом существенных особенностей. [c.11]
Поскольку существенных отличий в физическом механизме процессов в одно- и двуосных кристаллах нет, а математическая сложность уравнений для вторых весьма возрастает, ограничимся одноосными кристаллами (теорию для двуосных и магнитных кристаллов см. в [015] и работах [38, 39, 41]). [c.64]
Следует отметить, что описываемые явления типичны для большой группы кристаллов, обладающих одной оптической осью и называемых одноосными. Сложнее дело обстоит в двуосных кристаллах, где ни один из лучей не может быть отнесен к обыкновенному. Кроме того, существуют и такие кристаллы, в которых один из лучей поглощается сильнее другого. Это явление носит название дихроизма. [c.
 32]
32]В общем случае кристалл является двуосным, т. е. в нем имеются два направления, представляющие собой две оптические оси, ориентированные относительно главных осей кристалла под определенным для данного вещества углом а (см. рис. 17.18). Если угол а=0, то обе оптические оси совпадают и кристалл становится одноосным. Поляризационные явления в двуосных кристаллах значительно сложнее, чем в одноосных. Мы ограничимся лишь рассмотрением оптических свойств одноосных кристаллов. [c.46]
Если же два когерентных луча линейно поляризовать во взаимно перпендикулярных плоскостях, то они при встрече не создадут интерференционной картины. Именно этот случай наблюдается при двойном лучепреломлении в кристаллах. Лучи, образованные расщеплением падающего луча в кристаллах, являются, конечно, когерентными, однако эти лучи как в одноосных, так и в двуосных кристаллах поляризованы во взаимно перпендикулярных плоскостях. Это не единственный способ получения когерентных и взаимно перпендикулярно поляризованных колебаний. Достаточно поставить
[c.49]
Достаточно поставить
[c.49]
Более того, можно доказать, что под действием давления, приложенного в одном направлении, вещества, подобные каменной соли и плавиковому шпату, превратились бы в двуосный, кристалл (а не одноосный, как это имело бы место, например, в случае стекла). [c.251]
При одностороннем сжатии (растяжении) направление сжатия (растяжения) является выделенным и играет роль оптической оси возникающая при этом анизотропия соответствует одноосному кристаллу. При более сложных деформациях, например, двустороннем растяжении, образец становится как бы двуосным кристаллом. [c.313]
Помещая в оптическую систему установки (см. рис. 29.1) клин, вырезанный из кристалла так, чтобы его оптическая ось была бы парал-можно по расстоянию между максимумами найти угол клина. В случае, если наблюдение ведется в белом свете, то угол клина можно рассчитать по характеру окраски. Для определения других характеристик кристаллов измерения проводят при наблюдении интерференционных картин поляризованных лучей в сходящихся пучках. Остановимся на конкретных приемах, позволяющих исследовать некоторые оптические характеристики кристалла, используя оптическую схему, изображенную на рис. 29.9. Наблюдение коноскопических фигур дает возможность оценить характер кристалла (одноосный или двуосный), провести технологический контроль обработки кристалла, определить знак кристалла (положительный или отрицательный) и знак вращения плоскости поляризации (если кристалл оптически активен).
[c.248]
Остановимся на конкретных приемах, позволяющих исследовать некоторые оптические характеристики кристалла, используя оптическую схему, изображенную на рис. 29.9. Наблюдение коноскопических фигур дает возможность оценить характер кристалла (одноосный или двуосный), провести технологический контроль обработки кристалла, определить знак кристалла (положительный или отрицательный) и знак вращения плоскости поляризации (если кристалл оптически активен).
[c.248]
Если падающий свет естественный или поляризован по кругу, то при вращении николя интенсивность проходящего света меняться не будет. Для отличия одного случая от другого применяется пластинка в четверть волны (короче, /4) или компенсатор. Пластинка в четверть волны есть кристаллическая пластинка, которая вносит дополнительную разность фаз в я/2 между проходящими через нее лучами, поляризованными во взаимно перпендикулярных плоскостях. Эти плоскости определяют в плоскости пластинки два направления, называемые главными направлениями пластинки. Обычно пластинка Я,/4 вырезается из одноосного кристалла (например,-кварца) параллельно его оптической оси. Тогда дополнительная разность фаз в я/2 вносится между обыкновенным и необыкновенным лучами. Но пластинку Я,/4 можно изготовить и из двуосного кристалла, например слюды. В дальнейшем для определенности предполагается, что пластинка /4 вырезана из одноосного кристалла. В свете, поляризованном по кругу, разность фаз между любыми двумя взаимно перпендикулярными колебаниями равна н=я/2. Если на пути такого света поставить пластинку Я./4, то она внесет дополнительную разность фаз =Ья/2. Результирующая разность фаз получится О или я, и свет станет поляризованным линейно. Его можно полностью погасить поворотом николя. Если же падающий свет естественный, то он останется таковым и после прохождения через пластинку Я,/4. В этом случае гашения не будет.
[c.472]
Обычно пластинка Я,/4 вырезается из одноосного кристалла (например,-кварца) параллельно его оптической оси. Тогда дополнительная разность фаз в я/2 вносится между обыкновенным и необыкновенным лучами. Но пластинку Я,/4 можно изготовить и из двуосного кристалла, например слюды. В дальнейшем для определенности предполагается, что пластинка /4 вырезана из одноосного кристалла. В свете, поляризованном по кругу, разность фаз между любыми двумя взаимно перпендикулярными колебаниями равна н=я/2. Если на пути такого света поставить пластинку Я./4, то она внесет дополнительную разность фаз =Ья/2. Результирующая разность фаз получится О или я, и свет станет поляризованным линейно. Его можно полностью погасить поворотом николя. Если же падающий свет естественный, то он останется таковым и после прохождения через пластинку Я,/4. В этом случае гашения не будет.
[c.472]
По числу оптических осей первого рода кристаллы разделяются ра 1) двуосные, 2) одноосные и 3) оптически изотропные.
 Эта классификация совпадает с классификацией, основанной на числе оптических осей второго рода.
[c.507]
Эта классификация совпадает с классификацией, основанной на числе оптических осей второго рода.
[c.507]Является ли кристалл изотропным или анизотропным и, в последнем случае, одноосным или двуосным, определяется симметрией кристалла. Так, например, кристаллы с кубической [c.29]
До сих пор мы ограничивались рассмотрением одноосных кристаллов, у которых эллипсоид показателя преломления является эллипсоидом вращения. Рассмотрим теперь двуосные кристаллы, эллипсоид показателя преломления которых имеет три неравные оси. У таких кристаллов существуют три главных значения показателя преломления , Пу и Мы будем полагать, как обычно, tiz> Пу Пх. [c.35]
Одноосные и двуосные кристаллы. Проведенные опыты показывают, что в кристалле исландского шпата имеется одно-единстЕенное направление, вдоль к0Т0р010 двойного лучепреломления не происходит. Такие кристаллы называются одио-осными, а направление, вдоль кото[)ого не происходит двойного лучеиреломле-
[c. 226]
226]
С помощью лучевого эллипсоида анализируется ход лучей в анизотропной среде и дaet я определение одноосных и двуосных кристаллов. [c.267]
О Что такое оптическая ось Сколько оптических осей но-жет существовать в кристалле Что такое одноосные и двуосные кристаллы Опишите метод анализа распространения лучей в анизотропной среде с помощыо лучевого эллипсоида. [c.271]
Определение знака кристалла. Наблюдение в сходящемся пучке позволяет определить знак как одноосного так и двуосного кристалла, т. е. выяснить, является он положительным или отрицательным. Опишем сначала метод для случая одноосного кристалла. Образец представляет собой пластинку, вырезанную перпендикулярно оптической оси. При помещении пластинки в линейный полярископ наблюдаемая коноскопическая карти- [c.304]
Плоскость, содержащая падающий луч и оптическую ось одноосного кристалла, называется главнтлм сечением или главной пло-скостьк ) кристалла. В двуосных кристаллах иод главным сечением понимается плоскость, проходящая через обе оптические оси. Мами не будет рассматриваться вопрос двулучепреломления в двуосных кристаллах. Желающие ознакомиться с двулучепреломлением в двуосных кристаллах могут обратиться к специальной литературе.
[c.226]
В двуосных кристаллах иод главным сечением понимается плоскость, проходящая через обе оптические оси. Мами не будет рассматриваться вопрос двулучепреломления в двуосных кристаллах. Желающие ознакомиться с двулучепреломлением в двуосных кристаллах могут обратиться к специальной литературе.
[c.226]
КРИСТАЛЛЫ валентные (атомные) содержат в узлах кристаллической решетки нейтральные атомы (С, Ge, Те и др.), между которыми осуществляется гомеополярная связь, обусловленная квантово-механическим взаимодействием глобулярные представляют собой частный случай молекулярных кристаллов и имеют вид клубка полимеров жидкие обладают свойствами как жидкости (текучестью), так и твердого кристалла (анизотропией свойств) внутри малых объемов идеальные не имеют дефектов структуры иопные обладают гетерополярной связью между правильно чередующимися в узлах кристаллической решетки положительными и отрицательными ионами квантовые характеризуются большой амплитудой нулевых колебаний атомов, сравнимой с межатомным расстоянием металлические образуются благодаря специфической химической связи, возникающей между ионами кристаллической решетки и электронным газом (Си, А1 и др. ) молекулярные (Лг, СН , парафин и др.) формируются силами Ван-дер-Вальса, главным образом дисперсионными нитевидные вытянуты в одном направлении во много раз больше, чем в остальных оптические [активные поворачивают плоскость поляризации света вокруг падающего линейно поляризованного луча анизотропные обладают двойным лучепреломлением, состоящим в том, что луч света, падающий на поверхность кристалла, раздваивается в нем на два преломленных луча двуосные имеют две оптические оси, вдоль которых свет не испытывает двойного лучепреломления одноосные (имеющие одну оптическую ось отрицательные, в которых скорость обыкновенного светового луча меньше, чем скорость распространения необыкновенного луча положительные, в которых скорость распространения обьпсновенного светового луча больше, чем скорость распространения необыкновенного луча))] КРИСТАЛЛИЗАЦИЯ— образование кристаллов из паров, растворов, расплавов веществ, находящихся в твердом состоянии в процессе электролиза и при химических реакциях
[c.
) молекулярные (Лг, СН , парафин и др.) формируются силами Ван-дер-Вальса, главным образом дисперсионными нитевидные вытянуты в одном направлении во много раз больше, чем в остальных оптические [активные поворачивают плоскость поляризации света вокруг падающего линейно поляризованного луча анизотропные обладают двойным лучепреломлением, состоящим в том, что луч света, падающий на поверхность кристалла, раздваивается в нем на два преломленных луча двуосные имеют две оптические оси, вдоль которых свет не испытывает двойного лучепреломления одноосные (имеющие одну оптическую ось отрицательные, в которых скорость обыкновенного светового луча меньше, чем скорость распространения необыкновенного луча положительные, в которых скорость распространения обьпсновенного светового луча больше, чем скорость распространения необыкновенного луча))] КРИСТАЛЛИЗАЦИЯ— образование кристаллов из паров, растворов, расплавов веществ, находящихся в твердом состоянии в процессе электролиза и при химических реакциях
[c. 244]
244]
В одноосных кристаллах линейно поляризованный луч, идущий вдоль оптич. оси, испытывает вращение нлоскостн поляризации вследствие разницы скоростей волн с npaBoii и левой поляризации. В др. направлениях имеет место эллиптич. двупреломление, как и в двуосных кристаллах. При распространении линейно поляризованной волны в оптически изотропной гиро-тронной среде в любом направлении в ней распространяются две волны с круговой поляризацией — правой н лево11, имеющие различные скорости п соответственно различные показатели преломления. Поэтому плоскость поляризации линейно поляризованной волны но мере распространения в этой среде будет поворачиваться. [c.490]
В предыдущей главе было показано, что свет, распространяющийся в двулучепреломляющих кристаллах, представляет собой линейную суперпозицию двух независимых волн. Эти независимые волны характеризуются вполне определенными фазовыми скоростями и состояниями поляризации. Двулучепреломляющие кристаллы могут быть как одноосными, так и двуосными. Однако большинство широко используемых кристаллов, например, таких, как кальцит и кварц, являются одноосными. В одноосных кристаллах независи мые волны представляют собой обыкновенную и необыкновенную
[c.132]
Однако большинство широко используемых кристаллов, например, таких, как кальцит и кварц, являются одноосными. В одноосных кристаллах независи мые волны представляют собой обыкновенную и необыкновенную
[c.132]
Иногда встречаются кртсталлы, в которых равны два главных показателя преломления, т.е. i, j = х, у или z. В таких кртсталлах может наблюдаться некритический к угловым расстройкам, или 90-гралус-ный, синхронизм. В случае одноосного кристалла равенство двух главных показателей преломления означает, что соответствующие поверхности индексов для со и 2 со касаются друг друга. В результате синхронизм некритичен к любым угловым расстройкам вследствие близости фазовых скоростей волн разных частот вблизи точки касания. Поверхности индексов двуосных кристаллов имеют более сложную форму. При выполнении указанных выше условий синхронизм оказывается нечувствительным к изменению направления распространения света в одаой плоскости и чувствительным в другой.
 [c.155]
[c.155]Кристаллы соединения ВаО 4Б2О3 оптически отрицательные, одноосные или двуосные с малой величиной 2F и показателями светопреломления 1.594 и 7Vj5=1.559. [c.144]
Кристаллы соединения Ва0-4В20з оптически отрицательные, одноосные или двуосные с малой величиной 27° и показателями светопреломления Ж =1.594 и 7У р=1.559. [c.179]
Теперь легко понять происхождение двойного лучепреломления. Допустим, что плоская волна падает на плоскопараллельную пластинку из одноосного кристалла. При преломлении на первой поверхности пластинки волна внутри кристалла разделится на обыкновенную и необыкновенную. Эти волны поляризованы во взаимно перпендикулярных плоскостях и распространяются внутри пластинки в разных направлениях и с разными скоростями. Волновые нормали обеих волн лежат в плоскости падения. Обыкновенный луч, поскольку его направление совпадает с направлением- волновой нормали, также лежит в плоскости падения. Но необыкновенный луч, вообще говоря, выходит из этой плоскости. (В случае двуосных кристаллов деление на обыкновенную и необыкновенную волны теряет смысл — внутри кристал та обе войны необыкновенные . При преломлении волновые ьормали обеих волн, конечно, остаются в плоскости падения, однакооба луча, вообш,е говоря, выходят из нее.)
[c.460]
(В случае двуосных кристаллов деление на обыкновенную и необыкновенную волны теряет смысл — внутри кристал та обе войны необыкновенные . При преломлении волновые ьормали обеих волн, конечно, остаются в плоскости падения, однакооба луча, вообш,е говоря, выходят из нее.)
[c.460]
Для одноосного кристалла изохроматическая поверхность есть поверхность вращения вокруг оптической оси (рис. 281). В направлении оптической оси она уходит в бесконечность, так как для этого направления оба показателя преломления п и Па совпадают. В двуосных кристаллах таких направлений два (рис. 282). Это есть оптические оси, точнее — оси нормалей (см. 80). Мы не будем зани-ь аться выводом уравнения изохроматической поверхности, а ограничимся качественными соображениями. [c.487]
Фиг. 2.1. Форма матрицы кристаллографических классов. а—двуосные кристаллы 6—одноосные кристаллы в — изотропные кристаллы. Обозначения маленькая точка—коэффициент равен иулю квадрат—коэффициент равен нулю, если справедливо условие Клейнмана соединенные точки —коэффициенты чи сленно равны, ио для точек обозначенных светлыми и темными кружками, коэффициенты имеют противоположные знаки. Пунктирные соединения справедливы лишь при выполнении условия Клейнмана. В двуосных кристаллах коэффициенты не зависимы, если условие Клейнмана не выполняется. Пунктирные линии в классе 1 показывают влияние условия Клейнмана на эти 18 коэффнциентов, Пунктирные соединения справедливы лишь при выполнении условия Клейнмана. В двуосных кристаллах коэффициенты не зависимы, если условие Клейнмана не выполняется. Пунктирные линии в классе 1 показывают влияние условия Клейнмана на эти 18 коэффнциентов,
|
| Когда мы делаем растяжение
тест мы удлиняем образец при определенной скорость деформации путем приложения правого напряжения через петлю обратной связи. Теперь нам нужно несколько определений:
|
| |||||||||||||||||||
Для испытаний на растяжение вам понадобится
стандартизованный образец (см. рисунок справа; все стрелки указывают
четко определенные размеры) с размером, подходящим для вашей машины.Поскольку максимум
нагрузка на машину ограничена, образец не должен быть слишком большим —
тогда машина не может его сломать. рисунок справа; все стрелки указывают
четко определенные размеры) с размером, подходящим для вашей машины.Поскольку максимум
нагрузка на машину ограничена, образец не должен быть слишком большим —
тогда машина не может его сломать. Вам также необходимо измерить деформацию и напряжение с некоторой точностью. Есть много способов сделать это, но я не буду вдаваться в подробности. Конечно, ограничены и настройки скорости деформации. Для очень низких скорости деформации вам придется очень долго ждать, пока ваш образец, наконец, переломы; их также трудно измерить.Для очень больших скоростей деформации вы может потребоваться больший стресс, чем может выдержать машина. Конечно, нужно постоянно измерять деформацию и подавать результаты. в некоторую электронную петлю обратной связи, которая контролирует напряжение до величины необходимо для получения желаемой скорости деформации. | ||||||||||||||||||||
Контроль температуры тоже не из легких.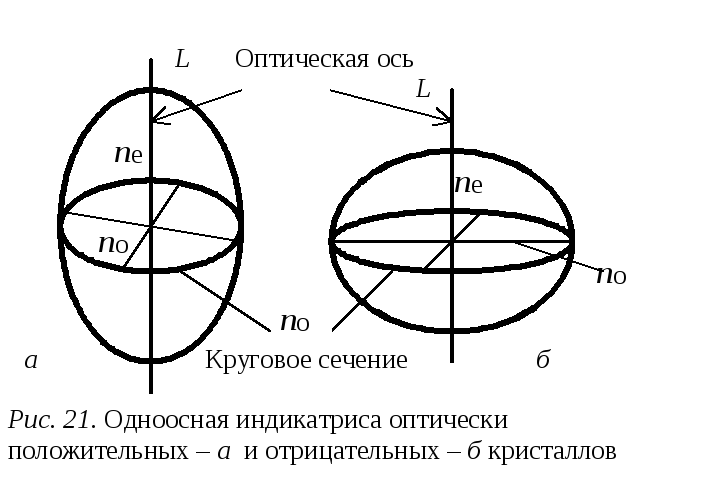 Вы можете поместить всю машину в комнату с определенной температурой, но это не так.
не слишком практично, если вы слишком сильно отклоняетесь от комнатной температуры.Это оставляет
только для создания «температурной камеры» вокруг образца, а не
простая задача, но выполнимая. Вы можете поместить всю машину в комнату с определенной температурой, но это не так.
не слишком практично, если вы слишком сильно отклоняетесь от комнатной температуры.Это оставляет
только для создания «температурной камеры» вокруг образца, а не
простая задача, но выполнимая. Хорошо — после того, как вы придумали несколько 100 000 долларов на покупку машины, нашли подходящее помещение и механический цех, который может придать образцу форму, вы можете Теперь приступим к одноосным испытаниям материалов. | ||||||||||||||||||||
Испытание на растяжение — Определения | ||||||||||||||||||||
Когда мы проведем испытание на растяжение, мы получим
диаграмму напряжения-деформации в результате.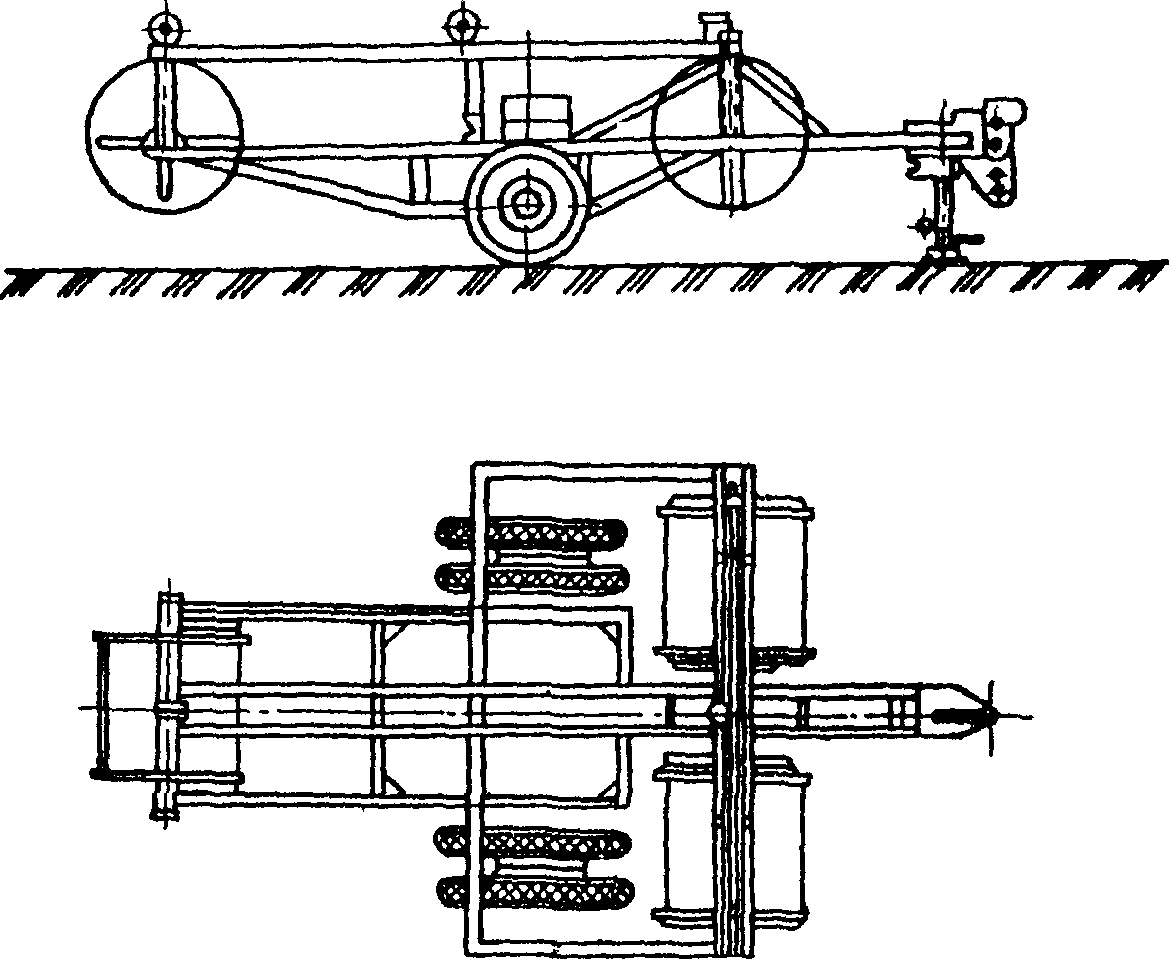 Ниже один (из какой-то стали), как он есть
из машины. Моя машина говорит по-немецки, поэтому я добавил переводы на
красный. Ниже один (из какой-то стали), как он есть
из машины. Моя машина говорит по-немецки, поэтому я добавил переводы на
красный. | ||||||||||||||||||||
| ||||||||||||||||||||
Машина показывает напряжение и
значения деформации для (конечной) прочности на разрыв и разрушения на
синие линии.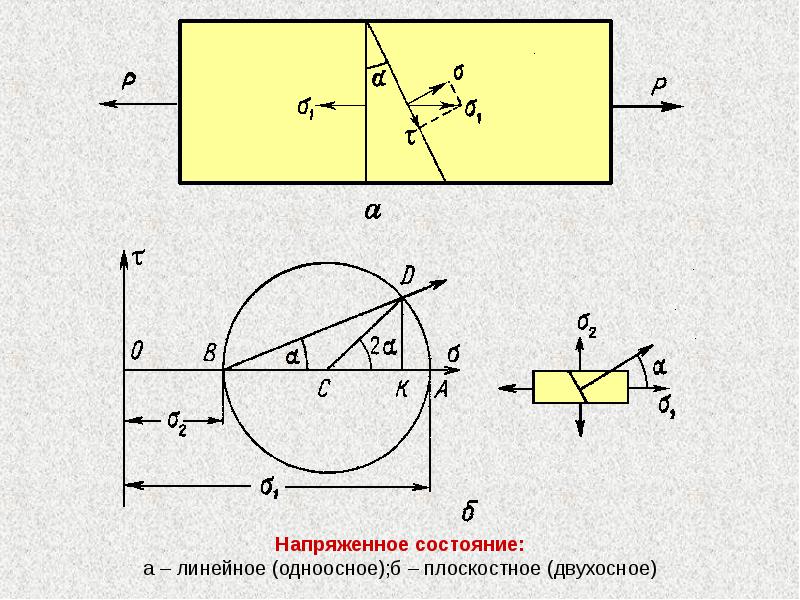 Он может это сделать, потому что достаточно умен, чтобы найти максимум
кривая и конец одного. Он может это сделать, потому что достаточно умен, чтобы найти максимум
кривая и конец одного. Это не указывает на критическую доходность прочность R P , потому что он недостаточно умен, чтобы обнаружить это. На самом деле, есть специальные определения и рецепты, чтобы прийти к номер для R P , но я не буду вдаваться в подробности. На показанной кривой видно расположение R P . но это не всегда так.Мы также видим, что некоторые странные вещи происходят в течение некоторого в то время как после R P было достигнуто. Кривая приобретает вид шаткий, и многое из этого сделано при реальных испытаниях. Нет ничего необычного в том, что кривая напряжение-деформация немного изгибается или проходит через небольшой пик, как только начинается пластическая деформация при R P . Это просто означает, что до пластика деформация может происходить в основном из-за вывих движения, вывихи должны быть сначала сформированы, либо оторваны от препятствий, сковывающих их, или и того, и другого.  Это происходит в некоторой степени
различные напряжения в разных частях образца, поэтому кривая
может стать «шумным». Это важное явление и неприятность.
Поскольку на данный момент мы еще не знаем, что такое дислокации, я вернусь
к этому моменту много
потом. Это происходит в некоторой степени
различные напряжения в разных частях образца, поэтому кривая
может стать «шумным». Это важное явление и неприятность.
Поскольку на данный момент мы еще не знаем, что такое дислокации, я вернусь
к этому моменту много
потом. | ||||||||||||||||||||
| Конечно, наклон напряжения s — штамм e кривая в упругой области дает Юнга
модуль прямо как s / e или лучше, так как мы
нет идеальной прямой линии, так как уклон Y = ds / de | ||||||||||||||||||||
| Максимум на любой кривой — полезный
вещь, потому что это легко обнаруживается и интерпретируется.В кривой напряжения-деформации
он обозначает предел прочности на разрыв R M , потому что,
как следует из этого слова, напряжение выше R M неизменно
произвести перелом. | ||||||||||||||||||||
| К сожалению, в science материалов, R M довольно неважно.Это означает стресс, которого на самом деле не существует в
материал. Легко понять почему. Машина для испытания на растяжение рассчитывает напряжение путем деления прилагаемой силы. на начальную площадь поперечного сечения образец. Это нормально для начала эксперимента, когда фактическая площадь поперечного сечения образца близка к исходному. Однако, поскольку образец растягивается намного выше предела текучести Дело в том, что он должен становиться тоньше, потому что его объем не может сильно измениться.В поперечное сечение, таким образом, уменьшается, и истинное значение Напряжение будет: приложенная сила, деленная на фактическую и меньшую площадь поперечного сечения.  | ||||||||||||||||||||
| Конечно, вычислить истинное напряжение s * (так мы это называем). Это всегда больше номинального напряжения s , которое используется машиной. Перебирая числа (при условии отсутствия изменения объема) получаем | ||||||||||||||||||||
Увы! Если мы перестроим кривую напряжения-деформации сейчас
для истинного напряжения полезный максимум составляет
ушел! Это одна из причин, почему мы обычно этого не делаем. Другая причина в том, что
в любом приложении напряжение истины равно
не имеющий отношения. Вы хотите знать, когда происходит сбой, относительно размеров
материал, который вы использовали, а не предполагаемые размеры. Другая причина в том, что
в любом приложении напряжение истины равно
не имеющий отношения. Вы хотите знать, когда происходит сбой, относительно размеров
материал, который вы использовали, а не предполагаемые размеры. | ||||||||||||||||||||
| Ситуация ухудшается. Из научного с точки зрения номинальной деформации мы использовали тоже не настоящая вещь. Нам нужен правда штамм . | ||||||||||||||||||||
| Почему это так? Представьте, что вы напрягаете свой образец
всего на 1%.Затем вы снова процедите его на 1%, и снова, и снова. После тебя
сделал это 10 раз, насколько велико общее количество напряжение? Если вы выберете 10 × 1% = 10%, вы, вероятно, небогатый человек. если ты получите 10% процентов на свой капитал в размере 100 $, сколько накопленных процентов делают у вас через 5 лет? 5 × 10% = 50%? Нет! По истечении первого года вы получаете 10 долларов процентов, а ваш капитал теперь составляет 110 долларов.  После второго года вы получите проценты в размере 11 долларов США.Ваш общий капитал после
5 лет — это (100 + 10 + 11 + 12 + 13 + 14) = 160 долларов, а ваш накопленный
проценты 60 $, а не 50 $. После второго года вы получите проценты в размере 11 долларов США.Ваш общий капитал после
5 лет — это (100 + 10 + 11 + 12 + 13 + 14) = 160 долларов, а ваш накопленный
проценты 60 $, а не 50 $. Это называется расчет сложных процентов и если вы когда-нибудь узнали об этом в школе, вы это ненавидели. | ||||||||||||||||||||
| Нам нужно сделать то же самое для напряжения, если мы хочу рассматривать истинную деформацию е * как конечную деформацию после деформации долота по битам.Конечно, снова (почти) легко вычислить, вот результат. | ||||||||||||||||||||
Извините. Страшные логарифмы поднимают свои уродливые
головы! Даже логарифм натуральный равен по основанию е! Страшные логарифмы поднимают свои уродливые
головы! Даже логарифм натуральный равен по основанию е! Вы либо знаете, что это значит, либо нет.Консультации этот модуль может освежит вашу память, но не заменит все (все же скорее элементарная) математика, которую вы могли быть лишены. | ||||||||||||||||||||
| Хотя мы обычно не строим Диаграммы деформирования с истинной деформацией либо он нам понадобится, как только мы рассчитаем свойства из напряженно-деформированного состояния. кривая как энергия разрушения . Или как только мы начнем сравнивать испытания на растяжение и сжатие, см. ниже. | ||||||||||||||||||||
| Есть еще одна вещь, которую мы можем Изучите форму одноосного тестирования: выше я сказал что образец становится тоньше, потому что его объем не может сильно измениться. То есть Конечно, правда, но вопрос, который мы задаем сейчас, — «насколько тонкий?» | ||||||||||||||||||||
| ||||||||||||||||||||
| Ну, мы не знаем, поэтому мы должны это измерить. Мы
иметь некоторую деформацию e 2 перпендикулярно
в направлении вытягивания и, следовательно, изменение длины на 1 + e 2 в геометрии, показанной выше. Поскольку
образец становится длиннее, но тоньше, e 2 должно быть отрицательным. У нас есть так называемое «боковое сужение , ». Измерение e 1 и e 2 позволяет определить новый материал параметр, называемый Пуассона передаточное отношение n | ||||||||||||||||||||
Теперь у вас должен быть вопрос:
«почему бы нам просто не вычислить n один раз и
для всех, при условии, что объем остается постоянным ». Ответ в том, что мы
сделай это, конечно. Результат: Ответ в том, что мы
сделай это, конечно. Результат: n (постоянный объем) = 0,5 . Отлично. Теперь посмотрим на измерил значений коэффициента Пуассона: | ||||||||||||||||||||
| ||||||||||||||||||||
Объем образца при испытании на растяжение,
очевидно, что , а не , остается постоянным. Не большой
иметь дело. Зачем это нужно? В конце концов, расстояние между атомами становится
значительно больше, когда вы их тянете. Не большой
иметь дело. Зачем это нужно? В конце концов, расстояние между атомами становится
значительно больше, когда вы их тянете. У нас нет выбора, кроме как жить с измеренными числами для коэффициента Пуассона. Да, он никогда не бывает далеко от 0,5 и, следовательно, не так важен, как модуль Юнга. это тем не менее необходимо для любых расчетов, которые пытаются сделать лучше, чем просто дать порядки величины. | ||||||||||||||||||||
Компрессионный Тестирование | ||||||||||||||||||||
При испытании на сжатие что-то новое может произойти , с которым мы должны иметь дело
во-первых: весь образец изгибается наружу на , находясь в
упругая область . Его длина в изогнутом состоянии примерно равна
он был без напряжения, но поскольку он изогнут, расстояние между двумя концами
меньше. Его длина в изогнутом состоянии примерно равна
он был без напряжения, но поскольку он изогнут, расстояние между двумя концами
меньше. Мы больше не проводим одноосные испытания! Это схематично показано на рисунок ниже. | ||||||||||||||||||||
| ||||||||||||||||||||
Вы, конечно, это знаете.Это может
случается, когда вы пытаетесь ударить что-то своим мечом. Понятно без
делать вычисления, что изгиб происходит легче для тонких образцов, чем
для приземистых. Расчеты, которые сделать не очень сложно, дают четкие
критерии изгиба при сжатии. Понятно без
делать вычисления, что изгиб происходит легче для тонких образцов, чем
для приземистых. Расчеты, которые сделать не очень сложно, дают четкие
критерии изгиба при сжатии. | ||||||||||||||||||||
| Для одноосных испытаний , однако, изгиб при сжатии не имеет значения, потому что, если это произойдет, у вас больше не будет одноосного тестирования. Ваш образец теперь испытывает сложные напряжения.На выпуклой стороне находится под растяжением напряжения, на вогнутой стороне он находится под напряжением сжатия, а в середине нет вообще никакого стресса. Нам это понадобится позже, так что это Хорошая идея сейчас посмотреть на следующую цифру и задуматься над ее значением: | ||||||||||||||||||||
| ||||||||||||||||||||
Если наш образец изгибается, как на рисунке выше,
внешняя (правая) часть будет испытывать растягивающее напряжение, так как она длиннее, чем
исходная длина. Точно так же внутренняя часть будет испытывать сжимающее напряжение; сейчас короче. Отсюда следует, что должна быть нейтральная деталь где-нибудь в интерьере без напряжения или деформации, так как ее длина не изменилось. В приведенном выше примере мы можем ожидать, что нейтральная часть верна. в центре. | ||||||||||||||||||||
| Такой лук не может быть под испытание на растяжение, и это одна из причин, почему мы предпочитаем испытание на растяжение.Если нам нужно провести испытание на сжатие, нам нужно сделать наш образец коротким и толстый, чтобы избежать «лука». Если мы сделаем это и теперь перейдем к обоим режимам, т.е. толкайте и вытягивайте, мы получаем кривые напряжения-деформации, как показано ниже. | ||||||||||||||||||||
| ||||||||||||||||||||
Переход от номинальных напряжений и деформаций к истинным напряжений и деформаций просто означает, что вы принимаете
учитывать, что площади поперечного сечения изменяются на во время деформации. Если вы удлините
образец становится тоньше, а если сжать, то толще. Стресс — это сила
разделены по площади, и мы должны это учитывать, чтобы быть точными.
Тогда все в порядке, за исключением того, что расчет истинного напряжения и деформации
на удивление сложно сделать! Таким образом, люди склонны придерживаться номинального значения стресса и напряжения , зная, что они могут
при необходимости всегда конвертируйте его. Если вы удлините
образец становится тоньше, а если сжать, то толще. Стресс — это сила
разделены по площади, и мы должны это учитывать, чтобы быть точными.
Тогда все в порядке, за исключением того, что расчет истинного напряжения и деформации
на удивление сложно сделать! Таким образом, люди склонны придерживаться номинального значения стресса и напряжения , зная, что они могут
при необходимости всегда конвертируйте его. | ||||||||||||||||||||
| Значит, я не обманул тебя, когда Я утверждал, что » кривая напряжения-деформации для не слишком больших напряжений ( дюйм испытание на сжатие ) выглядит так же, только в перевернутом виде, как при растяжении тестирование.Что ж, да — но только если вы избегаете поклона и немного постараетесь приспособиться для измененной геометрии. | ||||||||||||||||||||
| Регулировка геометрии — это то, что мы делаем, когда
перешла к истинному стрессу и напряжению. | ||||||||||||||||||||
| Одноосные испытания — это еще не все. затем бросается в глаза. Да, но не обманывайте себя.Я только поцарапал поверхность здесь. В этом простом эксперименте есть гораздо больше, чем я мог бы рассказать в этом коротком «научном» модуле. | ||||||||||||||||||||
Влияние приложенного одноосного напряжения на скорость и механические эффекты сшивки в тканевых биоматериалах
Конформационные изменения в коллагеновых фибриллах и, действительно, в тройной спирали могут быть вызваны приложением механического напряжения или деформации.Мы продемонстрировали, что скорость поперечного сшивания в гомобифункциональных реагентах на основе глутаральдегида и эпоксида может регулироваться одноосным напряжением (деформацией). Использовали два эпоксида поли (глицидилового эфира): Denacol EX-810 (небольшой бифункциональный реагент) и Denacol EX-512 (большой полифункциональный реагент). Чтобы предотвратить маскировку любого возможного эффекта за счет насыщения сайтов перекрестного сшивания, перикард крупного рогатого скота был перекрестно сшит до такой степени, что повышение температуры денатурации коллагена, Td, составляло половину максимального повышения, достигаемого с каждым реагентом.Во время сшивания было приложено одноосное растягивающее напряжение 0, 15, 124 или 233 кПа. Скорость поперечного сшивания (наблюдаемая по увеличению Td) увеличивалась с увеличением стресса до максимума при 124 кПа в глутаральдегиде при pH 7, но снижалась в EX-810 при pH 7. В каждом случае эффект был небольшим, но статистически значимым. Никакого эффекта не наблюдалось с большим EX-512. Сшивка при увеличении напряжения также показала систематическое влияние на механические свойства: уменьшение растяжимости и пластической деформации при одновременном увеличении прочности на разрыв.
Использовали два эпоксида поли (глицидилового эфира): Denacol EX-810 (небольшой бифункциональный реагент) и Denacol EX-512 (большой полифункциональный реагент). Чтобы предотвратить маскировку любого возможного эффекта за счет насыщения сайтов перекрестного сшивания, перикард крупного рогатого скота был перекрестно сшит до такой степени, что повышение температуры денатурации коллагена, Td, составляло половину максимального повышения, достигаемого с каждым реагентом.Во время сшивания было приложено одноосное растягивающее напряжение 0, 15, 124 или 233 кПа. Скорость поперечного сшивания (наблюдаемая по увеличению Td) увеличивалась с увеличением стресса до максимума при 124 кПа в глутаральдегиде при pH 7, но снижалась в EX-810 при pH 7. В каждом случае эффект был небольшим, но статистически значимым. Никакого эффекта не наблюдалось с большим EX-512. Сшивка при увеличении напряжения также показала систематическое влияние на механические свойства: уменьшение растяжимости и пластической деформации при одновременном увеличении прочности на разрыв. В каждом случае эффекты эпоксидов немного отличались от эффектов глутаральдегида. При подготовке к вышеуказанным экспериментам были проведены исследования влияния pH, температуры и времени выдержки для каждого эпоксида и (в меньшей степени) для глутарового альдегида. Опять же, систематические изменения механических свойств наблюдались с увеличением Td. Конформационные изменения коллагена, вызванные механическим напряжением (деформацией), модулируют скорость поперечного сшивания и результирующие механические свойства; однако эффекты чувствительны к используемому реагенту.
В каждом случае эффекты эпоксидов немного отличались от эффектов глутаральдегида. При подготовке к вышеуказанным экспериментам были проведены исследования влияния pH, температуры и времени выдержки для каждого эпоксида и (в меньшей степени) для глутарового альдегида. Опять же, систематические изменения механических свойств наблюдались с увеличением Td. Конформационные изменения коллагена, вызванные механическим напряжением (деформацией), модулируют скорость поперечного сшивания и результирующие механические свойства; однако эффекты чувствительны к используемому реагенту.
Одноосное испытание — обзор
3.1.3 Экспериментальное уплотнение карбонатной породы
При малых напряжениях экспериментальная механическая деформация карбонатной породы обычно характеризуется нелинейной зависимостью напряжения от деформации, которая интерпретируется как связанная с закрытием трещин , поры и другие дефекты (Vajdova, Baud, & Wong, 2004). Эта ранняя фаза может быть связана с in situ напряжениями, которым была подвергнута порода (Couvreur, Vervoort, King, Lousberg, & Thimus, 2001).![]() Расчеты скорости и добротности ультразвуковых продольных и поперечных волн, то есть оценка степени диссипации материала, позволяют отслеживать конец фазы закрытия трещины (Couvreur et al., 2001). Для пористости, заполненной рассолом, электропроводность снижается в начале испытания, что может быть связано с закрытием пор и субгоризонтальных трещин (Jouniaux, Zamora, & Reuschle, 2006). Используя модель Уолша (Walsh & Brace, 1966), нелинейная зависимость напряжения от деформации может быть связана с количеством трещин и различными типами пор (Baud, Schubnel, & Wong, 2000).После этой ранней фазы деформация характеризуется линейной упругой зависимостью напряжения от деформации. Эта линейно-упругая фаза может возникать на разных стадиях напряжения в зависимости от начальной пористости породы, степени цементирования и геометрии порового пространства.
Расчеты скорости и добротности ультразвуковых продольных и поперечных волн, то есть оценка степени диссипации материала, позволяют отслеживать конец фазы закрытия трещины (Couvreur et al., 2001). Для пористости, заполненной рассолом, электропроводность снижается в начале испытания, что может быть связано с закрытием пор и субгоризонтальных трещин (Jouniaux, Zamora, & Reuschle, 2006). Используя модель Уолша (Walsh & Brace, 1966), нелинейная зависимость напряжения от деформации может быть связана с количеством трещин и различными типами пор (Baud, Schubnel, & Wong, 2000).После этой ранней фазы деформация характеризуется линейной упругой зависимостью напряжения от деформации. Эта линейно-упругая фаза может возникать на разных стадиях напряжения в зависимости от начальной пористости породы, степени цементирования и геометрии порового пространства.
Вайдова и др. (2004) провели гидростатические трехосные испытания на трех различных известняках, основным структурным различием между которыми является их начальная пористость. Известняк Solnhofen имеет пористость 3%, пористость известняка Tavel — 10.4%, значения пористости известняков Индианы составляют 16%, 18% или 20%. Сжимаемость этих известняков увеличивается с увеличением пористости. Известняк Solnhofen имеет сжимаемость 0,016 ГПа -1 (Baud et al., 2000; Vajdova et al., 2004), известняк Tavel имеет сжимаемость 0,033 GPa -1 , а известняк Индианы имеет сжимаемость 0,075 GPa −1 (Вайдова и др., 2004). Для платформенных известняков со средней начальной пористостью 20% одноосные испытания показывают, что сжимаемость находится в диапазоне 0.01–0,2 ГПа –1 (Croizé, Ehrenberg, Bjørlykke, Renard, & Jahren, 2010b), и этот ранний диагенез был ответственен за чрезмерное уплотнение породы и хорошее сохранение пористости.
Известняк Solnhofen имеет пористость 3%, пористость известняка Tavel — 10.4%, значения пористости известняков Индианы составляют 16%, 18% или 20%. Сжимаемость этих известняков увеличивается с увеличением пористости. Известняк Solnhofen имеет сжимаемость 0,016 ГПа -1 (Baud et al., 2000; Vajdova et al., 2004), известняк Tavel имеет сжимаемость 0,033 GPa -1 , а известняк Индианы имеет сжимаемость 0,075 GPa −1 (Вайдова и др., 2004). Для платформенных известняков со средней начальной пористостью 20% одноосные испытания показывают, что сжимаемость находится в диапазоне 0.01–0,2 ГПа –1 (Croizé, Ehrenberg, Bjørlykke, Renard, & Jahren, 2010b), и этот ранний диагенез был ответственен за чрезмерное уплотнение породы и хорошее сохранение пористости.
Основным направлением экспериментальных исследований уплотнения карбонатных пород является начало возникновения разрушения и вид режима разрушения (рис. 3.5b). Распространение трещин в горных породах — важный механизм, который может вызвать уплотнение, но он также важен для потока жидкости.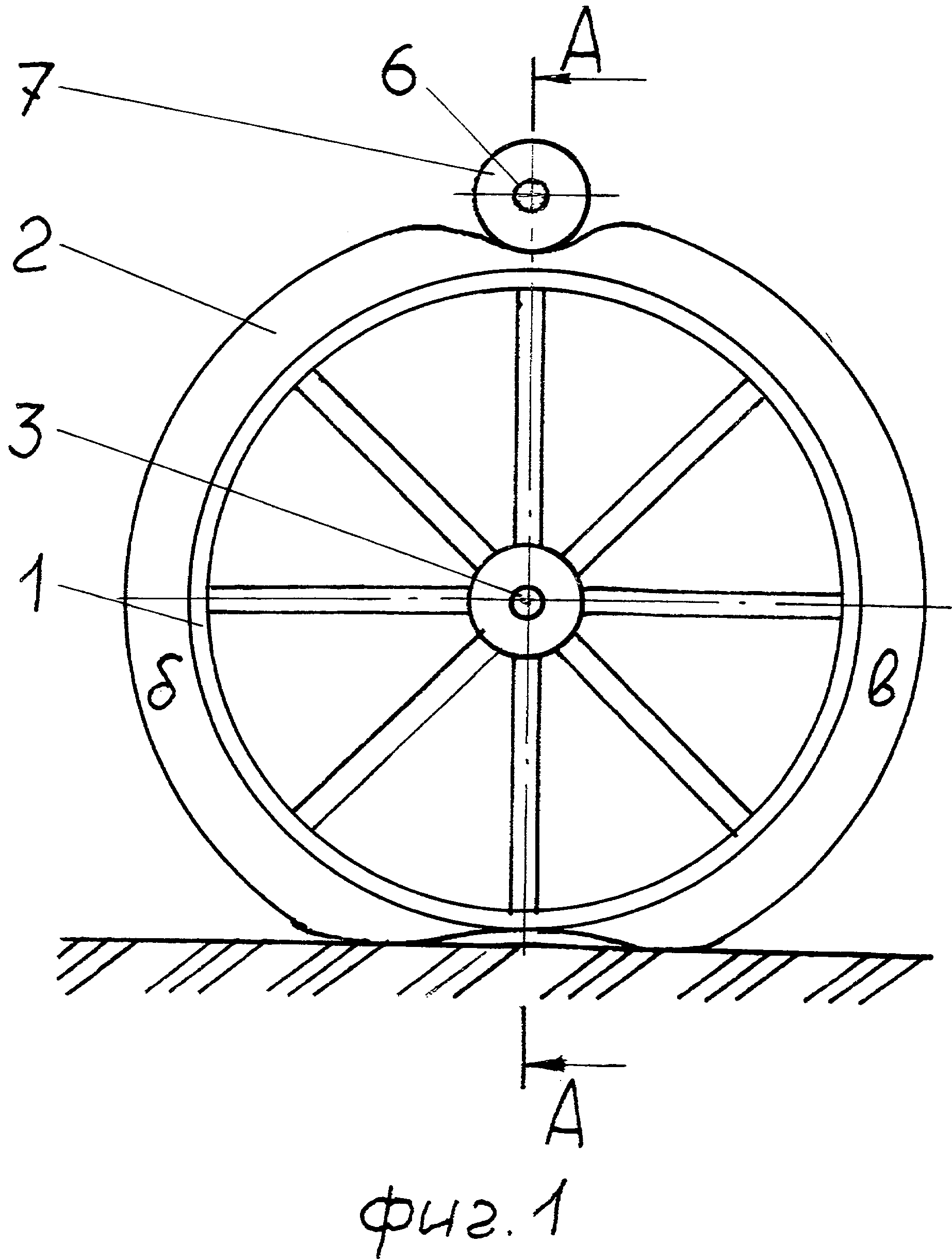 Плоскость разрушения создает путь для растворения и переноса вещества или может быть местом усиленной цементации и стать барьером для потока жидкости. Это приводит к последовательному поведению проницаемости во времени, от путей потока с высокой к низкой проницаемости.
Плоскость разрушения создает путь для растворения и переноса вещества или может быть местом усиленной цементации и стать барьером для потока жидкости. Это приводит к последовательному поведению проницаемости во времени, от путей потока с высокой к низкой проницаемости.
Нарушение контроля различных механических параметров в карбонатах. Эти пороупругие параметры обычно выводятся из механических трехосных испытаний (Baud et al., 2000; Palchik & Hatzor, 2002; Renner & Rummel, 1996; Vajdova et al., 2004), измерений распространения волн сжатия и сдвига (Couvreur et al. ., 2001; Эберли, Бэкле, Ансельметти и Инкзе, 2003 г .; Vanorio, Scotellaro, & Mavko, 2008), или измерения электропроводности в образцах, насыщенных флюидом (Jouniaux et al., 2006). Эти различные методы позволяют лучше ограничить механизмы, ответственные за механическое уплотнение карбонатов. Гидростатические трехосные испытания (Baud et al., 2000; Couvreur et al., 2001; Vajdova et al., 2004), испытания на одноосное сжатие (Croizé et al. , 2010b; Jouniaux et al., 2006; Palchik & Hatzor, 2002) , а также испытания на трехосное сжатие с различным ограничивающим давлением (Couvreur et al., 2001; Renner & Rummel, 1996) были выполнены на известняках и доломитах, некоторые экспериментальные данные показаны на рис. 3.5b – d. Испытанные карбонаты имели размер зерен от 5 до 400 мкм, различный химический состав, то есть кальцит, арагонит, доломит, и различное расположение порового пространства. Из-за различий в экспериментальных процедурах и микроструктурных свойствах тестируемых образцов разные тесты трудно сравнивать (Renner & Rummel, 1996). Критическое напряжение (то есть пиковое напряжение), при котором наблюдается постоянная деформация, варьируется от 5 до более 500 МПа в этих различных исследованиях.Пористость, по-видимому, является основным фактором, влияющим на начало разрушения, даже несмотря на то, что разброс критического напряжения в зависимости от пористости довольно велик (рис. 3.6). Одной из причин такого разброса может быть сложность системы пор в карбонатах (Lucia, 1995).
, 2010b; Jouniaux et al., 2006; Palchik & Hatzor, 2002) , а также испытания на трехосное сжатие с различным ограничивающим давлением (Couvreur et al., 2001; Renner & Rummel, 1996) были выполнены на известняках и доломитах, некоторые экспериментальные данные показаны на рис. 3.5b – d. Испытанные карбонаты имели размер зерен от 5 до 400 мкм, различный химический состав, то есть кальцит, арагонит, доломит, и различное расположение порового пространства. Из-за различий в экспериментальных процедурах и микроструктурных свойствах тестируемых образцов разные тесты трудно сравнивать (Renner & Rummel, 1996). Критическое напряжение (то есть пиковое напряжение), при котором наблюдается постоянная деформация, варьируется от 5 до более 500 МПа в этих различных исследованиях.Пористость, по-видимому, является основным фактором, влияющим на начало разрушения, даже несмотря на то, что разброс критического напряжения в зависимости от пористости довольно велик (рис. 3.6). Одной из причин такого разброса может быть сложность системы пор в карбонатах (Lucia, 1995). В известняках Tavel, Indiana, Majella, Solnhofen изучалось влияние типа пористости на развитие механического разрушения. Было обнаружено, что коллапс пор начинается в более крупных порах (Zhu et al., 2010). Для пород, содержащих как макро-, так и микропористость, макропоры определяют локализацию трещин (Вайдова и др., 2010). Эти исследования указывают на важность описания типа пористости при изучении механического уплотнения карбонатов. Когда образцы насыщены, вода выдавливается в трещины и способствует образованию субвертикальных трещин (Jouniaux et al., 2006). Следовательно, критическое напряжение ниже в водонасыщенных образцах (рис. 3.6).
В известняках Tavel, Indiana, Majella, Solnhofen изучалось влияние типа пористости на развитие механического разрушения. Было обнаружено, что коллапс пор начинается в более крупных порах (Zhu et al., 2010). Для пород, содержащих как макро-, так и микропористость, макропоры определяют локализацию трещин (Вайдова и др., 2010). Эти исследования указывают на важность описания типа пористости при изучении механического уплотнения карбонатов. Когда образцы насыщены, вода выдавливается в трещины и способствует образованию субвертикальных трещин (Jouniaux et al., 2006). Следовательно, критическое напряжение ниже в водонасыщенных образцах (рис. 3.6).
Рисунок 3.6. Критическое осевое напряжение в различных карбонатах в зависимости от пористости. График справа представляет собой увеличенное изображение нижней части графика напряжения левой стороны графика (все испытания проводились в сухих условиях, за исключением данных Jouniaux et al.(2006)).
Были определены различные виды отказов в зависимости от ограничивающего давления (Baud et al. , 2000; Renner & Rummel, 1996). При ограничивающем давлении ниже 50 МПа, т.е. эквивалентном глубине захоронения менее 3–4 км, дилатансия начиналась и действовала как предвестник хрупкого разлома. Для промежуточного удерживающего давления можно было измерить начальную стадию деформационного упрочнения. А при ограничении давлений выше 350 МПа образцы разрушались из-за катакластического течения, связанного с усиленным сдвигом уплотнением и деформационным упрочнением (Baud et al., 2000). Компактный катакластический поток обычно наблюдался как временное явление, которое развивалось с увеличением напряжения до дилатантного катакластического потока и, в конечном итоге, локализации сдвига (Baud et al., 2000). В очень пористых известняках наблюдалось критическое давление, при превышении которого поведение напряжения-деформации становится нелинейным, что соответствует схлопыванию пор и дроблению зерен (Vajdova et al., 2004).
, 2000; Renner & Rummel, 1996). При ограничивающем давлении ниже 50 МПа, т.е. эквивалентном глубине захоронения менее 3–4 км, дилатансия начиналась и действовала как предвестник хрупкого разлома. Для промежуточного удерживающего давления можно было измерить начальную стадию деформационного упрочнения. А при ограничении давлений выше 350 МПа образцы разрушались из-за катакластического течения, связанного с усиленным сдвигом уплотнением и деформационным упрочнением (Baud et al., 2000). Компактный катакластический поток обычно наблюдался как временное явление, которое развивалось с увеличением напряжения до дилатантного катакластического потока и, в конечном итоге, локализации сдвига (Baud et al., 2000). В очень пористых известняках наблюдалось критическое давление, при превышении которого поведение напряжения-деформации становится нелинейным, что соответствует схлопыванию пор и дроблению зерен (Vajdova et al., 2004).
Упругие, неупругие и разрушающие свойства карбонатных пород могут быть связаны с их пористостью, а сжимаемость карбонатов увеличивается с увеличением пористости. Критические напряжения для начала схлопывания пор при гидростатической и негидростатической нагрузке уменьшаются с увеличением пористости (Вайдова и др., 2004). В наиболее пористом известняке преобладает механическое двойникование, а в наиболее плотном известняке активируется дислокационное скольжение (Вайдова и др., 2004). Упругая жесткость и пористость являются основными параметрами, влияющими на начало расширения (Palchik & Hatzor, 2002).
Критические напряжения для начала схлопывания пор при гидростатической и негидростатической нагрузке уменьшаются с увеличением пористости (Вайдова и др., 2004). В наиболее пористом известняке преобладает механическое двойникование, а в наиболее плотном известняке активируется дислокационное скольжение (Вайдова и др., 2004). Упругая жесткость и пористость являются основными параметрами, влияющими на начало расширения (Palchik & Hatzor, 2002).
Помехи. фигурки из одноосных кристаллов
Интерфер. фигуры из одноосных кристалловПомехи.фигурки из одноосных кристаллов
В одноосных кристаллах интерференционная фигура образуется изогирой, состоящей из двух черных полос, пересекающихся под прямым углом, образующий крест, и различные изохроматические кривые, представленные концентрическими круги с интерференционными цветами, которые становятся все более яркими по мере того, как они добраться до периферии поля.
Чтобы узнать, есть ли в определенной точке на рисунке
принадлежит изогире (положение угасания) или изохроматической кривой
(общее положение) вам нужно только присоединить рассматриваемую точку к центру
креста; необычный компонент (эпсилон) будет вибрировать в
радиальное направление и обычный компонент (омега) будет вибрировать перпендикулярно
(по касательной к окружности). Если они совпадают с направлениями NS и EW,
это означает, что они принадлежат изогире, так как совпадают с направлениями
вибрации поляризатора и анализатора. Если они не совпадают, они
должен принадлежать изохроматической кривой.
Если они совпадают с направлениями NS и EW,
это означает, что они принадлежат изогире, так как совпадают с направлениями
вибрации поляризатора и анализатора. Если они не совпадают, они
должен принадлежать изохроматической кривой.
Интерференционные характеристики одноосных кристаллов меняются в зависимости от
к срезу минеральной плиты.
Основные направления реза минеральных плит
a = разрез перпендикулярно к оптической оси
b = разрез наклонен к оптике ось
c = вырез очень наклонен к оптике ось
d = разрез параллельно плоскости оптической оси
а.Вырезать перпендикулярно оптическая ось
Интерференционная фигура образована изогирой, составленной
двумя черными полосами, которые пересекаются под прямым углом, образуя крест, и
различными изохроматическими кривыми, представленными концентрическими окружностями с интерференцией
цвета, которые становятся все выше по мере приближения к периферии
поля.
Центр изогиры креста совпадает с центром поля микроскопа.
При повороте никаких изменений не происходит (не движется и не меняется). форма).
Этот показатель интерференции указывает на то, что это одноосный минерал.
б. Срез наклонный к оптике ось
Интерференционная фигура образована изогирой, составленной двумя черными полосами, которые пересекаются под прямым углом, образуя крест, и различными изохроматическими кривыми, представленными концентрическими окружностями с интерференцией цвета, которые становятся все выше по мере приближения к периферии поля.
Центр изогиры креста смещен от центра поля.
Чем больше наклон угол, тем дальше центр крест изогиры движется к периферии поля (участок «i» на рисунке).
Этот показатель интерференции указывает на то, что это одноосный минерал.
г.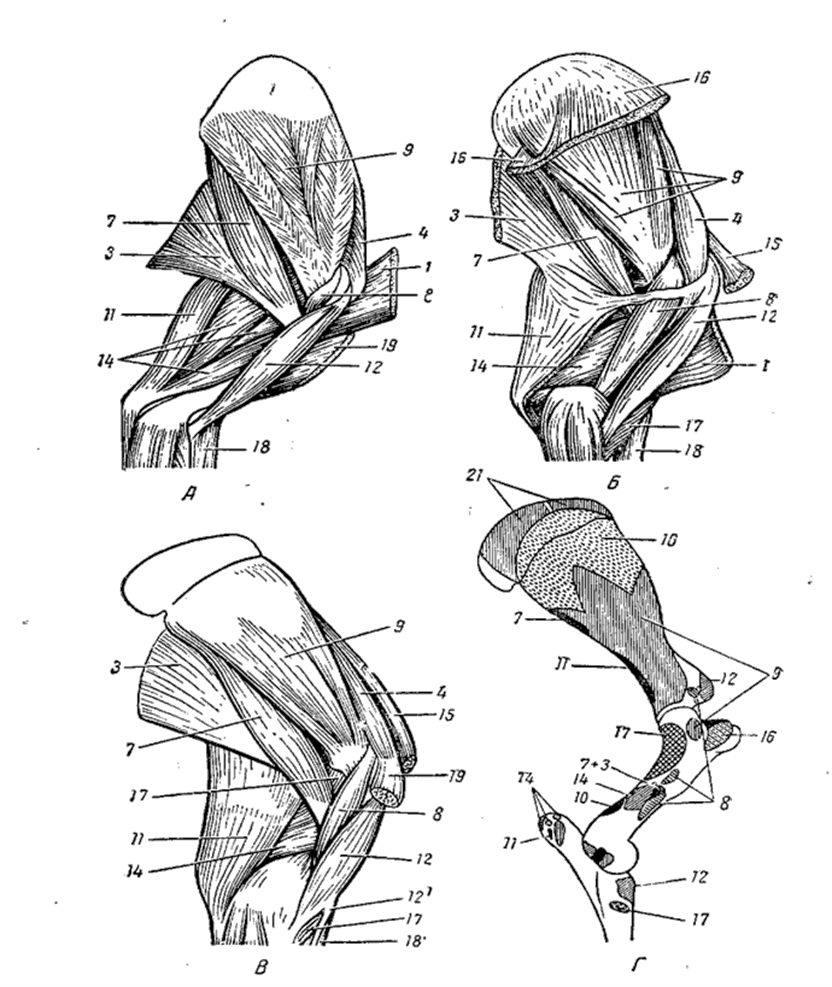 Крой очень склонен к
оптическая ось
Крой очень склонен к
оптическая ось
Интерференционная фигура образована изогирным крестом, центр находится вне поля зрения. Как оказалось, фигура видно по частям.
Видна единственная изогирная полоса, движущаяся по полю. зрения, пока он не исчезнет совсем. Иногда это вертикальная полоса изогирного креста, выходящего на поле, а иногда и горизонтального так делают.
Теоретически кристалл всегда можно идентифицировать как одноосный когда полосы остаются прямыми и не сгибаются при выходе с поля. Однако на практике может возникнуть некоторая путаница, и желательно искать другие зерна минерала с другой огранкой.
г. Вырезать параллельно плоскости оптической оси
Когда разрез параллелен оптической оси (оптические оси лежат в плоскости сечения) образуется фигура-вспышка, которая характеризуется крестообразной изогирой, состоящей из необычайно широких полос которые занимают почти все поле зрения. Однако когда микроскоп ступень даже немного перевернута (<5 °), полностью исчезает.
На рисунке не различаются одноосные и двухосные минералы.
Индекс | Введение | PPL | Ортопеды XPL | XPL conos | Предыдущий | Далее | верхний
Реакция на одноосное и двухосное растяжение-растяжение человеческой linea alba
https://doi.org/10.1016/j.jmbbm.2016.06.015Получить права и содержание выполнено на человеческой линии альба.Сравнивали механику тканей linea alba человека и свиньи.
Данные linea alba человека и свиньи существенно не различались для одноосных экспериментов.
В двухосных испытаниях на растяжение и напряжение наблюдалась определенная значимость.
Впервые здесь представлены испытания на растяжение белой линии человека на равноправное осевое растяжение.
Abstract
Существует мало исследований, посвященных поведению растяжения-стресса человеческой белой линии, однако понимание механики этой ткани важно для разработки более эффективных методов закрытия брюшной раны.Опубликованные данные касаются в основном белой линии свиней, а для тканей человека имеются противоречивые результаты и отсутствуют биаксиальные данные. Эта вариабельность, вероятно, связана с проблемами, связанными с физическими размерами ткани и различиями в экспериментальной методологии. В этом исследовании основное внимание уделялось механической характеристике растяжения белой линии живота человека с использованием одноосных и двухосных испытаний с равной нагрузкой, выполняемых с использованием методов измерения деформации на основе изображений. Были получены тринадцать свежезамороженных брюшных стенок человеческих трупов, которые использовали для подготовки 7 образцов как в поперечном, так и в продольном направлениях для одноосного тестирования и 13 квадратных образцов для двухосного тестирования.
Результаты показали значительную анизотропию, и для двухосных испытаний с равной нагрузкой деформация была сильно смещена в продольном направлении. По сравнению с аналогичными тестами на ткани свиньи из предыдущего исследования было обнаружено, что реакция белой линии свиней на одноосную нагрузку аналогична реакции белой линии свиней человека, без каких-либо статистически значимых различий. При двухосной нагрузке линии человека и свиньи не показали статистической значимости разницы между их средними значениями в поперечном направлении.Однако значительная разница наблюдалась в продольном направлении, и необходимо дальнейшее изучение соответствующих тканевых структур, чтобы лучше понять этот результат. Эти результаты предоставляют первые данные о свойствах биаксиального растяжения человеческой белой линии и могут помочь в улучшенной оценке механики закрытия ран.
Графический аннотация
Ключевые слова
Human linea alba
Одноосное натяжение
Двуосное натяжение
Человек против свиньи
Закрытие брюшной раны
Рекомендуемые статьи Цитирующие статьи (0)
ElseВсе права защищены.Рекомендуемые статьи
Ссылки на статьи
Как рассчитать цвет по спектру одноосных драгоценных камней
Рис. 1. Корунд является примером одноосного отрицательного минерала. Этот кристалл рубина в матрице из Могока, Мьянма, имеет длину примерно 6,15 см. Ограненный драгоценный камень представляет собой ненагретый рубин весом 3,22 карата, также произведенный в Могоке. Ограненный камень любезно предоставлен Джеффри Бергманом, Primagem. Фото Роберта Велдона / GIA.РЕФЕРАТ
Цвет — важнейшее качество цветных камней, которое широко обсуждается и изучается геммологами.Понимание цветовых характеристик драгоценного камня может дать научную основу для определения правильности его огранки. В этом исследовании используется видимая спектроскопия для определения неполяризованных спектров одноосного материала по поляризованным спектрам (о-лучи и е-лучи), чтобы предсказать цвет одноосного драгоценного материала при просмотре в любом направлении. На первый взгляд интуитивно понятный способ сделать это, добавив взвешенные количества спектров поглощения o-лучей и e-лучей, на самом деле не работает для оценки неполяризованных спектров.Математически и физически правильный способ восстановить эти неполяризованные спектры — это сложить взвешенные поляризованные спектры пропускания, а затем, при желании, преобразовать их обратно в поглощение. Этот метод позволяет точно предсказать цвет материала при просмотре в любом направлении, если известны поляризованные спектры и угол обзора относительно оси c. Этот метод был проверен путем сравнения с синтетическим сапфиром с V-образным подшипником и синтетическим хромсодержащим сапфиром, разрезанным на пластины (не ограненные драгоценные камни) под разными углами относительно оптической оси.
ВВЕДЕНИЕ
Большинство драгоценных камней представляют собой минералы с кристаллической структурой, демонстрирующей дальний порядок, такие как алмазы, рубины и сапфиры. Чтобы полностью понять их цветовое поведение, необходимо рассмотреть эти драгоценные материалы с точки зрения их кристаллографических характеристик. Все кристаллы можно разделить на три категории: изометрические, одноосные (см. Рисунок 1) и двухосные.
Поляризованный свет. Свет — это форма электромагнитного излучения, которую можно рассматривать как волны, движущиеся в одном направлении со скоростью света, при этом компоненты электрического и магнитного поля колеблются перпендикулярно направлению движения.Колориметрические свойства света, попадающего в наши глаза, определяются спектром длин волн, присутствующим в световом луче. В общем, белый свет, производимый солнцем или лампой накаливания, неполяризован, то есть компонент электрического поля не имеет предпочтительной ориентации, и каждое направление колебаний представлено одинаково. Когда неполяризованный свет проходит через одноосный или двухосный материал в направлении, не параллельном оптической оси, он разделяется на два разных луча, у которых направления колебаний электрического поля перпендикулярны друг другу (Tilley, 2020).Это можно увидеть, наблюдая одноосные или двухосные кристаллы с проходящим поляризованным светом, где в большинстве случаев мы будем наблюдать разные цвета с разной ориентацией (см. Рисунок 2). Это, в свою очередь, связано с тем, что большинство цветных одноосных или двухосных минералов будут по-разному поглощать свет при изменении ориентации поляризации электрического поля света.
Рис. 2. Изображения полированной пластины из синтетического розового сапфира, сфотографированные при различных условиях поляризованного освещения.Слева: составляющая электрического поля, перпендикулярная оптической оси (E⊥c или o-ray). Справа: составляющая электрического поля, параллельная оптической оси (E || c или e-ray).
Цвет из спектра. Восприятие цвета людьми-наблюдателями определяется тремя основными факторами: условиями освещения, зрительной системой человека и самим объектом. Колориметрия — это область исследования, которая занимается количественным описанием восприятия цвета. Цветовые стимулы прозрачных материалов (например,g., драгоценные камни) будет зависеть от того, какие длины волн света проходят через материал в видимом диапазоне (приблизительно 380–780 нм). На рисунке 3 показан спектр поглощения синтетического розового сапфира, который показывает, какие длины волн неполяризованного света избирательно поглощаются материалом (высокие значения поглощения), а какие длины волн поглощаются меньше (низкое поглощение). Термин плеохроизм используется для описания явления, при котором свет с разными направлениями поляризации дает разные цвета из-за различий в способе поглощения поляризованного света одноосными или двухосными минералами (Hughes, 2014).Для одноосного минерала существует два уникальных направления колебаний электрического поля: либо перпендикулярно оптической оси 1 (o-луч), либо параллельно оптической оси (e-луч). (Обратите внимание, что в этой рукописи мы используем терминологию o-ray и e-ray, которая эквивалентна терминологии E⊥c и E || c, более часто используемой в минералогической литературе.) Для одноосных материалов, таких как На рубине спектр поглощения изменяется с направлением поляризации от о-лучей к е-лучам (рис. 4).
Рис. 3. Для неполяризованного спектра видимого света образца синтетического розового сапфира (вверху справа), снятого под определенным углом падения, рассчитанный цвет показан под образцом. Расчет основан на функции согласования цветов CIE 1931 года (CIE, 1932) и освещении D65.Цвет воспроизводится на основе цветового пространства sRGB. Рубиновая пластина имеет толщину 2,754 мм и концентрацию хрома 111 ppma.
Рис. 4. Поляризованные спектры оптически ориентированной пластины из синтетического рубина (такие же, как на рисунках 2 и 3) с поляризованными направлениями o-лучей (синяя линия) и e-ray (оранжевая линия), а также неполяризованного света (зеленая линия ).
Воспринимаемый цвет света после прохождения через полированную пластину из любого одноосного материала может быть рассчитан с использованием спектров пропускания (как поляризованных, так и неполяризованных) и угла падающего света относительно оси c в сочетании со спектральным распределением мощности исходных условий освещения. (например, освещение D65, эквивалентное дневному свету, или освещение лампами накаливания), а также функции чувствительности человеческого зрения, которые описывают, как комбинация длин волн, достигающих глаза, преобразуется в цвет.
Как правило, большинство источников света неполяризованы. Поэтому при определении воспринимаемого цвета наиболее целесообразно рассматривать любой материал в неполяризованном свете. Для одноосных минералов, когда неполяризованный свет проходит параллельно оптической оси, все лучи являются эквивалентными o-лучами, с направлением колебаний электрического поля, перпендикулярным оптической оси. Однако, когда неполяризованный свет проходит через материал перпендикулярно оптической оси, он разделяется на два разных луча: o-луч и e-луч, колеблющиеся перпендикулярно и параллельно оптической оси соответственно.Когда неполяризованный свет проходит через одноосный материал в любом случайном направлении, он также разделяется на два луча, при этом один луч вынужден колебаться вдоль o-луча, а другой — перпендикулярно как направлению колебаний o-луча, так и траектории движения лучей. луч света. Однако, основываясь на знаниях авторов, точные способы определения неполяризованного спектра поглощения одноосного минерала в любом общем направлении до сих пор четко не выяснены. Как будет продемонстрировано в последующих разделах, интуитивно понятные средства смешивания спектров поглощения o-лучей и e-лучей , взвешенные в соответствии с геометрией любого общего направления, неверны и не могут воспроизводить экспериментально измеренные спектры.В этой статье мы демонстрируем, что необходимо использовать взвешенные комбинации спектров пропускания o-лучей и e-лучей, чтобы определить спектр поглощения и, следовательно, цвет одноосного минерала для заданного угла входного луча освещения и обзора. угол.
МАТЕРИАЛЫ И МЕТОДЫ
Образцы. Образцы синтетического рубина и сапфира были предоставлены исследовательской лабораторией GIA в Карловых Варах. Все образцы были изготовлены в виде пластин с покрытием оптического качества.Ориентация кристаллов хорошо контролировалась устройством для ориентации двухосных кристаллов, описанным Thomas et al. (2014).
UV-Vis-NIR Спектроскопия. Поляризованные УФ-видимые спектры были получены с помощью специально модифицированного спектрофотометра Hitachi U-2910. Спектры регистрировали в диапазоне 190–1100 нм со спектральным разрешением 1 нм при скорости сканирования 400 нм / мин. Неполяризованные спектры были получены с помощью спектрофотометра PerkinElmer Lambda 950 UV-Vis (PE 950) в диапазоне 200–1000 нм, также со спектральным разрешением 1 нм.Мы также проверили степень поляризации неполяризованного света, генерируемого PE 950. Результаты показали, что PE 950 может производить идеальный неполяризованный свет (см. Рамку A), что означает, что неполяризованные спектры подходят для спектрального анализа. Как поляризованные, так и неполяризованные спектры были получены в лаборатории GIA в Карловых Варах.
Вставка A: Введение в соотношения стабильных изотопов кислорода и водорода |
Степень поляризации (DOP) — это в основном величина, используемая для описания части поляризованного луча света.DOP определяется следующим уравнением: , где I min и I max — минимальная и максимальная интенсивности света во всем диапазоне направлений поляризации соответственно. Идеально поляризованный луч света имеет DOP 100%, в то время как DOP 0% представляет собой совершенно неполяризованный свет. В этом исследовании для сбора неполяризованных спектров использовался спектрофотометр PerkinElmer Lambda 950 UV-Vis. В этом приборе есть съемный поляризатор, и мы снимали неполяризованные спектры без него.Однако в наиболее часто используемых спектрофотометрах отражение луча от решетки и другой оптики делает свет частично поляризованным. По этой причине спектрофотометр, использованный в данном исследовании, включал деполяризатор после решетки. Тем не менее, любой потенциально слегка неполяризованный свет может повлиять на результаты измерений. Для тестирования нашего спектрофотометра PerkinElmer Lambda 950 мы выбрали срез синтетического рубина в качестве пластины, ориентированной на 60 ° от оптической оси, и собрали неполяризованные спектры с тремя различными углами поворота относительно поверхности среза пластины (0 °, 45 ° и 90 °). .Любые значительные различия между этими спектрами предполагают, что «неполяризованный» свет на самом деле частично поляризован. Если между спектрами нет разницы, это будет означать, что в спектрофотометре отсутствует собственная поляризация света. На рисунке A-1 показаны неполяризованные спектры трех различных углов вращения, и этот эксперимент подтвердил, что свет в этом спектрофотометре полностью неполяризован. Следовательно, мы можем использовать измеренные неполяризованные спектры для расчета цвета. Рисунок A-1. Неполяризованные спектры оптически ориентированной пластины синтетического рубина (60 ° от оптической оси) с углами поворота 0 ° (синяя линия), 45 ° (оранжевая линия) и 90 ° (зеленая линия). |
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Это исследование началось со случайного открытия.В 2018 году ведущий автор (CS) работал стажером-исследователем в карловарской лаборатории GIA, изучая хромофоры в корунде. Сначала все спектры UV-Vis для корунда были собраны с использованием спектрофотометра Hitachi U-2910, который установлен в GIA только для сбора поляризованных спектров. Однако автор также хотел одновременно собрать некоторые неполяризованные спектры с целью вычисления цвета, наблюдаемого в неполяризованном свете. Чтобы сэкономить время, мы выдвинули гипотезу, что можно воссоздать неполяризованные спектры поглощения корундовой пластины в общей ориентации с взвешенными версиями спектров поглощения o-лучей и e-лучей.Например, свет, движущийся перпендикулярно оптической оси, будет разделен на два ортогональных луча, и прогнозировалось, что неполяризованный спектр будет равен сумме половины спектра поглощения o-лучей и половины спектра поглощения e-лучей (см. Уравнение 1):
A неполяризованный = 0,5 × A o-ray + 0,5 × A e-ray (1)Для проверки этой гипотезы был использован спектрофотометр PerkinElmer Lambda 950 UV-Vis. сбор неполяризованных спектров ванадийсодержащего сапфира с неполяризованным светом, движущимся перпендикулярно оптической оси.Сапфир, содержащий ванадий, обладал сильным плеохроизмом, что означало большие различия между спектрами o-лучей и e-лучей. Следовательно, если предсказанные и измеренные спектры хорошо согласуются, мы могли бы сделать вывод, что гипотеза верна. Измеренные и прогнозируемые спектры (с использованием взвешенных спектров поглощения, как в уравнении 1) показаны на рисунке 5. Из-за значительной разницы между расчетным и измеренным спектрами мы определили, что эта гипотеза неверна и неполяризованный спектр поглощения не может быть восстановлен соответствующим образом. взвешенные версии спектров поглощения о-лучей и е-лучей.
Рис. 5. Измеренные (синяя линия) и оцененные (красная пунктирная линия) спектры поглощения. Расчетный метод был основан на взвешенных комбинациях спектров поглощения o-лучей и e-лучей (что было признано недействительным методом).
На этом этапе мы поняли, что прогнозирование неполяризованных спектров поглощения сложнее, чем мы первоначально думали.В этом исследовании мы объясняем, почему мы не можем использовать взвешенные комбинации спектров поглощения o-лучей и e-лучей для определения спектра неполяризованного поглощения. Кроме того, мы также предлагаем разумный метод для предсказания спектров поглощения в любой общей ориентации. Ключ к этому методу состоит в том, что все расчеты должны основываться на спектрах пропускания, а не на спектрах поглощения. К этому решению можно прийти интуитивно, поскольку сложение двух разных спектров поглощения математически требует, чтобы весь свет одновременно поглощался обоими спектрами поглощения.Например, если мы сложим вместе спектр поглощения Cr и V, чтобы представить материал, содержащий Cr и V, полный свет одновременно поглощается Cr и V. Однако, учитывая расщепление света на два поляризованных луча в одноосном материала, два луча света независимы, и каждый луч не видит другого. Чтобы математически смоделировать это, необходимо преобразовать поглощение в пропускание, чтобы эффективно разделить эти два луча света. См. Обсуждение ниже.
Неполяризованный свет, идущий параллельно оптической оси .В случае кубических кристаллов показатели преломления падающего света в любом направлении поляризации идентичны (Tilley, 2020). Однако, когда мы имеем дело с одноосными кристаллами, показатели преломления о-лучей и е-лучей не равны. Луч света, проходящий через одноосный кристалл, разделяется на два ортогональных луча, каждый со своим показателем преломления. Когда свет движется параллельно оптической оси, он будет колебаться во всех направлениях, перпендикулярных пути светового луча. Рисунок 6 демонстрирует это с одноосным материалом, представленным эллипсоидом, определяемым показателями преломления света o-лучей и e-лучей.Оптическая ось на этой диаграмме вертикальна, а поперечное сечение, перпендикулярное оптической оси, представляет собой круг с радиусом, равным показателю преломления o-луча (n o ). Следовательно, когда свет проходит через одноосный материал вдоль оптической оси, он колеблется перпендикулярно оптической оси.
Рисунок 6.Луч света, падающий на одноосную отрицательную индикатрису (n o > n e ) с направлением движения, параллельным оптической оси (зеленая пунктирная линия).
Неполяризованный свет, движущийся перпендикулярно оптической оси. Когда свет движется перпендикулярно оптической оси, он разделяется на два луча с ортогональными направлениями электрического поля. В этом случае для одноосного кристалла поперечное сечение индикатрисы представляет собой эллипс, а не круг (рисунок 7).Один из разделенных лучей будет иметь направление колебаний электрического поля, параллельное оптической оси (e-луч), в то время как другой луч будет колебаться перпендикулярно оптической оси (o-луч). Свет, идущий в этом направлении, будет в равной степени разделен на о-лучи и е-лучи.
Рисунок 7.Луч света, падающий на одноосную отрицательную индикатрису (n o > n e ) с направлением движения, перпендикулярным оптической оси.
Лучше всего об этом подумать, рассматривая интенсивность или лучистый поток падающего света, разделяемого пополам между о-лучом и электронным лучом. Связь между коэффициентом пропускания и лучистым потоком может быть выражена уравнением 2:
где
- T — коэффициент пропускания
- Φ t — передаваемый лучистый поток через материал
- Φ i — начальный лучистый поток, получаемый материалом
Поскольку o-лучи и e-лучи получают по половине лучистого потока, падающего на материал, уравнение 2 можно переписать как:
где
- Φ t o-ray — переданный лучистый поток, связанный с o-лучом
- Φ t e-ray — это переданный лучистый поток, связанный с e-ray
Уравнение 3 математически показывает, почему простое сложение спектров поглощения, как в уравнении 1, неверно, поскольку существует логарифмическое соотношение между пропусканием и поглощением: A = –log (T) .Чтобы проверить нашу формулу, неполяризованный свет был использован для измерения ванадийсодержащей сапфировой пластины с гранями, вырезанными и отполированными параллельно оптической оси. Затем мы сравнили измеренный спектр с рассчитанным на основе уравнения 3, используя измеренные спектры поглощения o-лучей и e-лучей, преобразованные в коэффициент пропускания. Результаты показаны на рисунке 8. Из рисунка 8 видно, что оцененный спектр хорошо согласуется с измеренным спектром. Мы также можем вычислить цвет из оцененного спектра и измеренного спектра, а также из спектра, оцененного методом использования взвешенных спектров поглощения (уравнение 1).Эти три цвета воспроизведены на рисунке 9. Значение цветовой разницы ∆E 00 (Luo et al., 2001) между правильно оцененным и измеренным спектрами составляет 0,80, в то время как ∆E 00 между неправильно оцененным и измеренный спектр равен 1,79, что демонстрирует точность использования спектров пропускания для предсказания цвета.
Рисунок 8.Спектры пропускания оптически ориентированной пластины (ось c параллельно полированным граням) сапфира, содержащего ванадий. Предполагаемый неполяризованный спектр (красная пунктирная линия) рассчитывается на основе уравнения 3.
Рис. 9. Сгенерированный цвет, где нижняя треть рассчитывается на основе измеренного спектра, левая треть — на основе правильно оцененного спектра, а правая треть — на основе неправильно оцененного спектра.
Падение неполяризованного света в случайном направлении. При рассмотрении луча света, проходящего через одноосный материал в любом общем направлении относительно оси c, ситуация немного сложнее. Тем не менее, мы все еще можем использовать каркас, разработанный в предыдущих разделах, для покрытия образцов, измеренных с полированной поверхностью, параллельной и перпендикулярной оптической оси, с использованием неполяризованного света. Из оптической индикатрисы, показанной на рисунке 10, очевидно, что когда свет, проходящий через одноосный материал в общем направлении, разделяется на два луча, один из них может быть описан как o-луч, а другой луч (k) — смесь o-ray и e-ray.Основываясь на законе Малуса (Collett, 2005), составляющая разделенного света (k) вдоль направлений поляризации o-лучей и e-лучей может быть вычислена в соответствии с уравнением 4:
I k = sin 2 θ × I o + cos 2 θ × I e (4)где
- I представляет интенсивность света вдоль указанной поляризации
- θ — угол между поперечным сечением (см. Также рисунок 10) и оптической осью
Поскольку коэффициент пропускания пропорционален интенсивности света 2 , уравнение 4 может быть переписано как уравнение 5, а окончательное уравнение для расчета неполяризованного спектра в любом общем направлении может быть выражено как уравнение 6:
T неполяризованный (k) = sin 2 θ × T o-ray (k ) + cos 2 θ × T e-ray (k ) ( 5)T неполяризованный = 0.5 × T o-ray +0,5 × (sin 2 θ × T o-ray + cos 2 θ × T e-ray ) (6)
Когда свет распространяется параллельно оптической оси, θ = 90 °, sin 2 θ = 1, cos 2 θ = 0, и уравнение 6 равно T o-ray . Когда свет движется перпендикулярно оптической оси, θ = 0 °, sin 2 θ = 0, cos 2 θ = 1, и уравнение 6 равно уравнению 3.
Чтобы проверить точность уравнения 6, авторы выбрали высококачественный однородный синтетический рубин и разрезали его на четыре двусторонние полированные пластины.Эти четыре пластины были точно ориентированы с помощью устройства для ориентации двухосных кристаллов, описанного Thomas et al. (2014). Углы между полированными поверхностями четырех пластин и оптической осью составляют 0 °, 30 °, 45 ° и 60 ° соответственно. Для этих четырех образцов были измерены неполяризованные спектры, а также поляризованные спектры (о-лучи и е-лучи) от образца 0 °. Измеренные спектры и оценочные спектры (основанные на уравнении 6) показаны на рисунке 11, показывая, что оцененные спектры хорошо согласуются с измеренными спектрами.Следовательно, уравнение 6 можно использовать для восстановления неполяризованного спектра образца одноосного материала под любым известным углом относительно оси c из спектров о-лучей и е-лучей. Кроме того, колориметрические данные, а также значения ∆E 00 показаны в таблице 1. Очень маленькие значения ∆E 00 для всех четырех проверенных углов демонстрируют высокую точность оцененных спектров и по величине аналогичны ожидаемая неопределенность между двумя измерительными приборами. Чтобы получить представление о величине значений ∆E 00 , повторяемость прибора для однородных образцов без замены на одном приборе составляет порядка 0.05–0.10, воспроизводимость измерений в разное время или на разных инструментах составляет порядка 0,5–1,0, а пороги восприимчивости для цветовых различий составляют порядка 1,0–2,0. Точные величины зависят от однородности образцов, конкретного инструмента, геометрии измерения и условий просмотра, таких как фон, цвет освещения и уровень освещенности (Berns, 2019).
Рисунок 10.Луч света, падающий на одноосную отрицательную индикатрису (n o > n e ) в любом общем направлении, где I представляет интенсивность света, а θ — угол между поперечным сечением (оранжевый эллипс) и оптическая ось. Интенсивность луча света, колеблющегося перпендикулярно o-лучу (k-луч на рисунке), может быть выражена как квадрат функций косинуса и синуса θ.
Рисунок 11.Измеренные спектры (красная линия) и оценочные спектры (черная пунктирная линия) для образца при углах 0 °, 30 °, 45 ° и 60 ° между полированными гранями и оптической осью.
Рис. 12. Спектры неполяризованного пропускания (зеленая линия) сапфира, содержащего ванадий, и вклад каждого поляризованного луча (o-луч = синяя линия, e-ray = оранжевая линия) под разными одинаковыми углами (0.0, 22,5 °, 45,0 °, 67,5 °, 90,0 °) относительно оптической оси.
Поскольку взаимосвязь между разными углами и неполяризованными спектрами измерялась напрямую, трехмерный график, на котором угол падения (θ) нанесен на спектры пропускания (o-лучи, e-лучи и неполяризованные), чтобы продемонстрировать изменение вклада каждого поляризованный луч (не полный коэффициент пропускания) под разными углами представлен на рисунке 12.
ВЫВОДЫ
Неполяризованные спектры одноосных материалов в любом направлении могут быть восстановлены из квадрата функций косинуса и синуса o-лучей и e-лучей, при условии, что угол падающего света θ относительно оси c (оптической оси) известен.Эта расчетная функция, выраженная в уравнении 6, была получена теоретически и проверена экспериментально. Распространение этой теоретической основы с полированных пластин на ограненные драгоценные камни представляет собой серьезную проблему и станет предметом будущих исследований.
Об авторахМистер.Шен — аспирант лаборатории науки о цвете Манселла в Рочестерском технологическом институте (RIT) по специальности «наука о цвете». Доктор Палке — старший менеджер по исследованию цветных камней, а г-н Сан — научный сотрудник GIA в Карлсбаде, Калифорния. Доктор Фэйрчайлд — профессор и глава-основатель Интегрированной академии наук в Научном колледже RIT, а также директор Программы науки о цвете и Лаборатории науки о цвете Манселла. Он является членом Общества науки и технологий в области визуализации (IS&T) и Оптического общества Америки (OSA).
БлагодарностиАвторы хотели бы поблагодарить трех анонимных рецензентов, а также Натана Ренфро из GIA и Троя Ардона, которые предоставили много полезных комментариев и предложений.Этот исследовательский проект спонсируется программой исследовательской стажировки GIA.
использованная литератураБернс Р.С. (2019) Принципы цветовой технологии Биллмейера и Зальцмана . John Wiley & Sons, Хобокен, Нью-Джерси.
CIE (1932) Международная комиссия по освещению в порядке преемственности на заседании Международной фотометрической комиссии, 1931 год. Издательство Кембриджского университета, Кембридж, Великобритания.
Collett E. (2005) Полевое руководство по поляризации . SPIE, Беллингем, Вашингтон.
Хехт Э. (2001) Оптика . Аддисон-Уэсли, Ливан, Индиана.
Hughes R.W. (2014) Плеохроизм в ограненных камнях: Введение. G&G , Vol. 50, No. 3, pp. 216–226, http://dx.doi.org/10.5741/GEMS.50.3.216
Луо М.Р., Цуй Г., Ригг Б. (2001) Разработка CIE 2000 Формула цветоразличия: CIEDE2000. Исследование и применение цвета , Vol. 26, No. 5, pp. 340–350, http://dx.doi.org/10.1002/col.1049
Thomas T., Rossman GR, Sandstrom M. (2014) Устройство и метод оптического ориентирования двухосных кристаллов. для пробоподготовки. Обзор научных инструментов , Vol. 85, № 9, с. 093105, http://dx.doi.org/10.1063/1.4894555
Тилли Р.Дж. (2020) Цвет и оптические свойства материалов . John Wiley & Sons, Ltd., Хобокен, Нью-Джерси.
Испытание на одноосное растяжение — ASM International
Испытание на растяжение является одним из наиболее часто используемых тестов для оценки материалов.В простейшей форме испытание на растяжение выполняется путем захвата противоположных концов испытательного образца (образца) внутри силовой рамы испытательной машины. Машина прикладывает растягивающее усилие, что приводит к постепенному удлинению и, в конечном итоге, к разрушению испытательного образца. Во время процесса обычно отслеживаются и записываются данные о силе растяжения — количественная мера того, как образец для испытаний деформируется под действием приложенной силы растяжения. При правильном проведении испытание на растяжение обеспечивает данные о силе растяжения, которые могут количественно определить несколько важных механических свойств материала.Эти механические свойства, определенные в результате испытаний на растяжение, включают, помимо прочего, следующее: свойства упругой деформации, такие как модуль упругости (модуль Юнга) и коэффициент Пуассона; Предел текучести и предел прочности при растяжении; Свойства пластичности, такие как удлинение и уменьшение площади; Характеристики деформационного упрочнения
- Источник: Испытания на растяжение, второе издание (ASM International)
- Опубликовано: 1 декабря 2004 г.
- Страницы: 31
- Тип обзора: экспертная оценка
Документ Скачать Доступ
Для доступа к электронный (PDF) документ, который был приобретен, документ появится в MyASM My Content.(Вы должны войти на сайт, чтобы получить доступ к приобретенному вами контенту).
Вы также можете получить доступ к приобретенному документу, выполнив поиск и нажав кнопку «Загрузить» на странице сведений о продукте документа.
Примечание : После загрузки вами цифрового контента ASM и оплаты любых применимых сборов ASM International предоставляет вам неисключительное право просматривать, использовать и отображать такой Контент неограниченное количество раз исключительно на вашем персональном компьютере или персональном устройстве. и исключительно для вашего личного некоммерческого использования.Цифровой контент ASM предоставляется вам по лицензии, а не продается. Вы не можете продавать, сдавать в аренду, сдавать в аренду, распространять, транслировать, сублицензировать или иным образом передавать какие-либо права на Контент или любую его часть какой-либо третьей стороне, а также вы не можете удалять или изменять какие-либо уведомления о правах собственности или ярлыки на Контенте.



 Шасси
Шасси 0.
0. Средства наземного транспорта, летательные аппараты, плавучие средства и относящиеся к транспорту устройства и оборудование (Группы 86-89)
Средства наземного транспорта, летательные аппараты, плавучие средства и относящиеся к транспорту устройства и оборудование (Группы 86-89)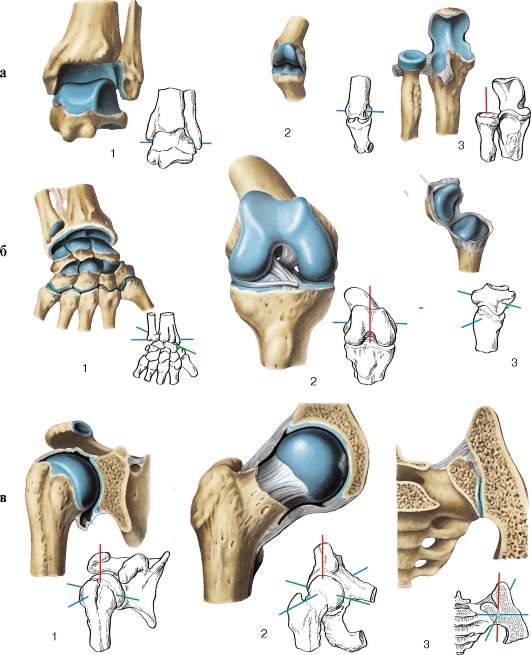 ..
.. l (s) — длина образца при нанесении
напряжение с; л 0 начальная
длина или л 0 = л (с
= 0) . Штамм — это сущность без единицы!
l (s) — длина образца при нанесении
напряжение с; л 0 начальная
длина или л 0 = л (с
= 0) . Штамм — это сущность без единицы! 