Эллипс. Полуоси эллипса. Фокус эллипса.
- Альфашкола
- Статьи
- Эллипс
Эллипс- замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. На рисунке ниже показано несколько примеров.
Круг-это частный случай эллипса, который получается, когда сечение через конус или цилиндр ортогонально оси конуса или цилиндра.
Эллипс-это фигура, в результате сечения конуса и прямого кругового цилиндра
Эллипс симметричен относительно горизонтальной и вертикальной осей, как показано на рисунке выше. Максимальное расстояние между двумя точками происходит вдоль горизонтальной оси (называемой главной осью или поперечным диаметром), а минимальное расстояние между двумя точками-вдоль вертикальной оси (называемой малой осью или сопряженным диаметром).
Полуось — это та часть оси, которая лежит между центром \(C\) и периметром эллипса — называется полуосью. Полуоси, принадлежащие к главной оси — большая полуось, а полуось, принадлежащих к малой оси — малая полуось. На приведенной выше рисунке мы обозначили каждую из двух полуосей \(a\) и каждую из двух полуосей \(b\). Точки, показанные красным цветом по периметру эллипса, являются точками, где большая и малая оси пересекают периметр эллипса. Это вершины эллипса. Вершины — это точки, в которых кривизна эллипса максимальна (т. е. где главная ось пересекает периметр эллипса).
Есть две специальные точки, которые лежат на главной оси эллипса, равноудаленной от его центра C, каждая из которых является фокусом эллипса. Эти две точки (совместно называемые фокусами эллипса) обычно обозначаются как \(F1\) и \(F2\). Расположение фокусов таково, что для любой точки \(p\) по периметру эллипса сумма расстояний от \(F1\) до \(P\) и от \(F2\) до \(P\) остается постоянной и будет равна длине главной оси. Фактически, принимая любую произвольную пару точек в качестве фокусов и любое значение длины главной оси, которое больше расстояния между этими двумя точками, соответствующий эллипс определяется как набор точек, для которых сумма расстояний между точкой и каждым из фокусов равна длине главной оси.
Эти две точки (совместно называемые фокусами эллипса) обычно обозначаются как \(F1\) и \(F2\). Расположение фокусов таково, что для любой точки \(p\) по периметру эллипса сумма расстояний от \(F1\) до \(P\) и от \(F2\) до \(P\) остается постоянной и будет равна длине главной оси. Фактически, принимая любую произвольную пару точек в качестве фокусов и любое значение длины главной оси, которое больше расстояния между этими двумя точками, соответствующий эллипс определяется как набор точек, для которых сумма расстояний между точкой и каждым из фокусов равна длине главной оси.
Сумма расстояний от фокусов до любой точки эллипса есть постоянная
Расстояние между любым из фокусов и центром эллипса называется фокусным расстоянием и будет зависеть от длины главной и малой осей. Мы обозначили отрезки линии, соединяющие каждый фокус с центром эллипса \(C\). Длину\( c\) (т. е. Фокусное расстояние) можно найти по следующей формуле:
\(с= \sqrt{a^2-b^2} \)
где \(a\) и \(b\)-длины главной и малой осей соответственно.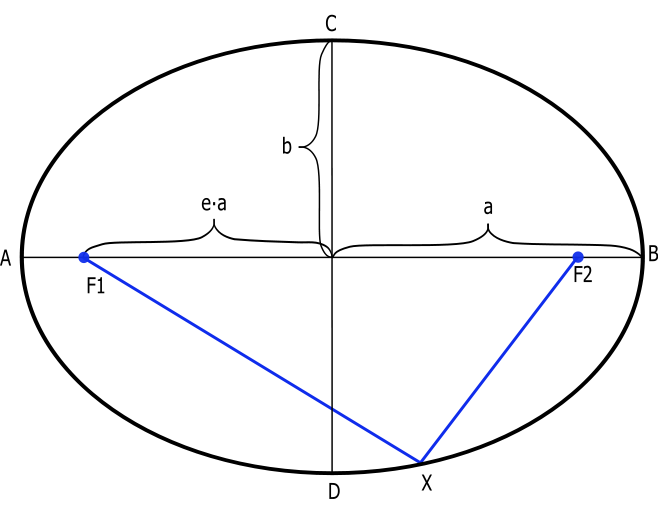 Обратите внимание, что чем дальше фокусы от центра эллипса, тем меньше сходство между эллипсом и окружностью. Кривизна в вершинах эллипса будет увеличиваться, в то время как кривизна в \(cо\)-вершинах будет уменьшаться. Другими словами, эллипс станет более плоским по мере увеличения значения \(c\).
Обратите внимание, что чем дальше фокусы от центра эллипса, тем меньше сходство между эллипсом и окружностью. Кривизна в вершинах эллипса будет увеличиваться, в то время как кривизна в \(cо\)-вершинах будет уменьшаться. Другими словами, эллипс станет более плоским по мере увеличения значения \(c\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Алексей Сергеевич Макейчик
Репетитор по математике
Стаж (лет)
Образование:
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Виктор Дмитриевич Ильин
Репетитор по математике
Стаж (лет)
Образование:
ГОУ ВО Луганский государственный университет имени Владимира Даля, Кафедра теории и практики перевода германских и романских языков факультета филологии и массовых коммуникаций
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Валерия Сергеевна Архипова
Репетитор по математике
Стаж (лет)
Образование:
МГУ им. А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор по химии для подготовки к ОГЭ
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор по английскому языку для подготовки к ОГЭ
- Английский язык для начинающих
- Репетитор по английскому для взрослых
- Репетитор для подготовки к ВПР по русскому языку
- Репетитор по биологии для подготовки к ОГЭ
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ЕГЭ
Похожие статьи
- Умножение и деление дробей
- Формулы окружности
- Математические факты о Парфеноне в Греции
- Типы четырехугольников
- Как перевести квадратные сантиметры в квадратные метры
- Задачи на координатной решетке.
 2}$, точки $(c,0), \, (-c,0)$ называют фокусами эллипса. Величину $\varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 \leq \varepsilon \leq 1$.
2}$, точки $(c,0), \, (-c,0)$ называют фокусами эллипса. Величину $\varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 \leq \varepsilon \leq 1$.  
Рис 5: Эллипс и его директрисы.
 
Опишем сначала элементарные свойства эллипса, следующие непосредственно из канонического уравнения (19).
1. Из этого уравнения следует, что если точка $(x,y)$ принадлежит эллипсу, то выполняются неравенства $|x| \leq a $, $|y| \leq b$. Таким образом, все точки эллипса лежат в этом прямоугольнике (конечном!).
2. Так как переменные $x,y$ входят в уравнение эллипса только в квадратах, то из того, что $(x,y)$ лежат на эллипсе следует, что точки $(\pm x, \, \pm y)$ также лежат на эллипсе при любом выборе знаков. Это означает, что эллипс симметричен при отражении относительной осей координат и имеет центр симметрии, точку $O$.
 2}{4}=1. \] Через точку $(1,1)$ провести хорду, делящуюся в этой точке пополам.
2}{4}=1. \] Через точку $(1,1)$ провести хорду, делящуюся в этой точке пополам. 
3.4 Прямая на плоскости 3.6 Гипербола
 
Большая полуось — Academic Kids
From Academic Kids
В геометрии большая полуось (также большая полуось ) a применяется к эллипсам и гиперболам.
Содержимое 1 Эллипс
2 Гипербола
3 Астрономия
3.1 Период обращения
3.2 Среднее расстояние
3.3 Энергия; расчет большой полуоси по векторам состояния4 Пример
5 Каталожные номера
Эллипс
Большая полуось эллипса — это половина большой оси, проходящей от центра через фокус к краю эллипса. Большая ось — это самая длинная линия, проходящая через центр и оба фокуса эллипса, причем ее концы находятся в самых широких точках формы.

Он связан с малой полуосью
- среднее по времени r -1 a -1
Энергия; расчет большой полуоси по векторам состояния
В астродинамике большая полуось
и
где:
-
v\, — орбитальная скорость от вектора скорости орбитального объекта, -
\mathbf{r }\, -
G \, — гравитационная постоянная, -
M \, масса центрального тела. 
Обратите внимание, что для данного центрального тела и полной удельной энергии большая полуось всегда одна и та же, независимо от эксцентриситета. Наоборот, для данного центрального тела и большой полуоси полная удельная энергия всегда одинакова.
Пример
Период обращения Международной космической станции составляет 91,74 минуты, следовательно, большая полуось составляет 6738 км [1] ( http://www.google.com/search?num=100&hl=en&lr=&newwindow=1&safe=off&q=%28%2891.74*60%2F2%2Fpi%29%5E2*398600%29%5E%281%2F3% 29 ). Каждая дополнительная минута соответствует ок. Еще 50 км: дополнительные 300 км длины орбиты занимают 40 секунд, на меньшую скорость приходится еще 20 секунд.
Ссылки
- Джереми Б. Татум, Небесная механика, Глава 9. Задача двух тел в двух измерениях (2004) ( http://orca.phys.uvic.ca/~tatum/celmechs/celm9.pdf )
- Даррен М. Уильямс, Среднее расстояние между звездой и планетой на эксцентрической орбите , Американский журнал физики, ноябрь 2003 г.
 , том 71, выпуск 11, стр. 1198–1200 ( http://scitation.aip. org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000071000011001198000001&idtype=cvips&gifs=yes )bg:Голяма полуос
, том 71, выпуск 11, стр. 1198–1200 ( http://scitation.aip. org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000071000011001198000001&idtype=cvips&gifs=yes )bg:Голяма полуос
pl:płoś wielka fr: Полувеликий топор это: Semiasse maggiore тр: Ана Эксен
Большая полуось | Космическая Вики
в: Конические сечения, Астродинамика, Небесная механика
Посмотреть источник File:Semimajoraxis.pngБольшая полуось эллипса
В геометрии термин большая полуось (также большая полуось ) используется для описания размеров эллипсов и гипербол.
Содержимое
- 1 Эллипс
- 2 Гипербола
- 3 Астрономия
- 3.1 Период обращения
- 3.2 Среднее расстояние
- 3.3 Энергетика; расчет большой полуоси по векторам состояния
- 4 Пример
- 5 Каталожные номера
Эллипс
Большая ось эллипса — это его самый длинный диаметр, линия, проходящая через центр и оба фокуса, причем ее концы находятся в самых широких точках формы. Большая полуось составляет половину большой оси и, таким образом, проходит от центра, через фокус и к краю эллипса.
9{2}\,\!}.
Большая полуось составляет половину большой оси и, таким образом, проходит от центра, через фокус и к краю эллипса.
9{2}\,\!}.
Парабола может быть получена как предел последовательности эллипсов, в которой один фокус остается фиксированным, а другой может перемещаться произвольно далеко в одном направлении, сохраняя фиксированным ℓ{\ displaystyle \ ell \, \!}. Таким образом, a{\displaystyle a\,\!} и b{\displaystyle b\,\!} стремятся к бесконечности, a{\displaystyle a\,\!} быстрее, чем b{\displaystyle b\,\!}.
Большая полуось представляет собой среднее значение наименьшего и наибольшего расстояний от одного фокуса до точек эллипса. Теперь рассмотрим уравнение в полярных координатах, с одним фокусом в начале координат, а другим в положительном 9{3}/\mu }}}
, где:
- a{\displaystyle a\,} — длина большой полуоси орбиты
- μ{\ displaystyle \ mu} — стандартный гравитационный параметр.
Обратите внимание, что для всех эллипсов с заданной большой полуосью период обращения одинаков, независимо от эксцентриситета.
В астрономии большая полуось является одним из наиболее важных элементов орбиты, наряду с ее периодом обращения. Для объектов Солнечной системы большая полуось связана с периодом орбиты третьим законом Кеплера (первоначально полученным эмпирическим путем), 9{3}\,}
, где G — гравитационная постоянная, M — масса центрального тела, а m — масса вращающегося тела. Как правило, масса центрального тела настолько больше массы вращающегося тела, что m можно не учитывать. Делая это предположение и используя типичные астрономические единицы, мы получаем более простую форму, открытую Кеплером.
Примечательно, что траектория тела на орбите вокруг барицентра и его траектория относительно основной массы являются эллипсами. большая полуось , используемая в астрономии, всегда представляет собой расстояние от первичной до вторичной; таким образом, параметры орбит планет даны в гелиоцентрических терминах. Разницу между первоцентрической и «абсолютной» орбитами лучше всего можно проиллюстрировать, взглянув на систему Земля-Луна. Отношение масс в этом случае равно 81,30059. Характерное расстояние Земля-Луна, большая полуось геоцентрической лунной орбиты , составляет 384 400 км. С другой стороны, барицентрическая лунная орбита имеет большую полуось 379°.,700 км, контрорбита Земли занимает разницу, 4700 км. Средняя барицентрическая орбитальная скорость Луны составляет 1,010 км/с, а у Земли — 0,012 км/с. Сумма этих скоростей дает геоцентрическую среднюю орбитальную скорость Луны 1,022 км/с; такое же значение можно получить, рассматривая только значение геоцентрической большой полуоси.
Отношение масс в этом случае равно 81,30059. Характерное расстояние Земля-Луна, большая полуось геоцентрической лунной орбиты , составляет 384 400 км. С другой стороны, барицентрическая лунная орбита имеет большую полуось 379°.,700 км, контрорбита Земли занимает разницу, 4700 км. Средняя барицентрическая орбитальная скорость Луны составляет 1,010 км/с, а у Земли — 0,012 км/с. Сумма этих скоростей дает геоцентрическую среднюю орбитальную скорость Луны 1,022 км/с; такое же значение можно получить, рассматривая только значение геоцентрической большой полуоси.
Среднее расстояние
Часто говорят, что большая полуось — это «среднее» расстояние между главной (фокусом эллипса) и вращающимся телом. Это не совсем точно, так как зависит от среднего значения. 9{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (удельная орбитальная энергия)
и
μ = GM {\ displaystyle \ mu = GM \,} (стандартный гравитационный параметр),
где:
- v {\ displaystyle v \,} — орбитальная скорость от вектора скорости орбитального объекта,
- р {\ displaystyle \ mathbf {r} \,} — декартов вектор положения находящегося на орбите объекта в координатах системы отсчета, относительно которой должны быть рассчитаны элементы орбиты (например, геоцентрический экваториальный для орбиты вокруг Земли, или гелиоцентрическая эклиптика для орбиты вокруг Солнца),
- G{\displaystyle G\,} — гравитационная постоянная,
- M{\displaystyle M\,} масса центрального тела.



 2}$, точки $(c,0), \, (-c,0)$ называют фокусами эллипса. Величину $\varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 \leq \varepsilon \leq 1$.
2}$, точки $(c,0), \, (-c,0)$ называют фокусами эллипса. Величину $\varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 \leq \varepsilon \leq 1$. 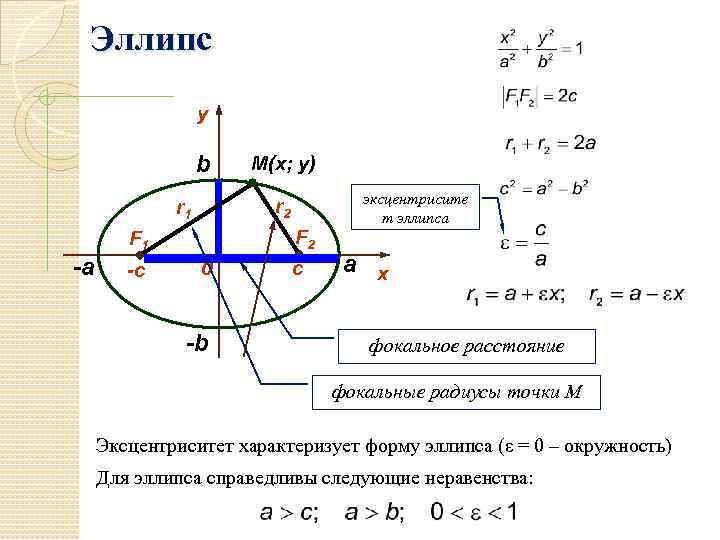


 , том 71, выпуск 11, стр. 1198–1200 ( http://scitation.aip. org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000071000011001198000001&idtype=cvips&gifs=yes )bg:Голяма полуос
, том 71, выпуск 11, стр. 1198–1200 ( http://scitation.aip. org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000071000011001198000001&idtype=cvips&gifs=yes )bg:Голяма полуос