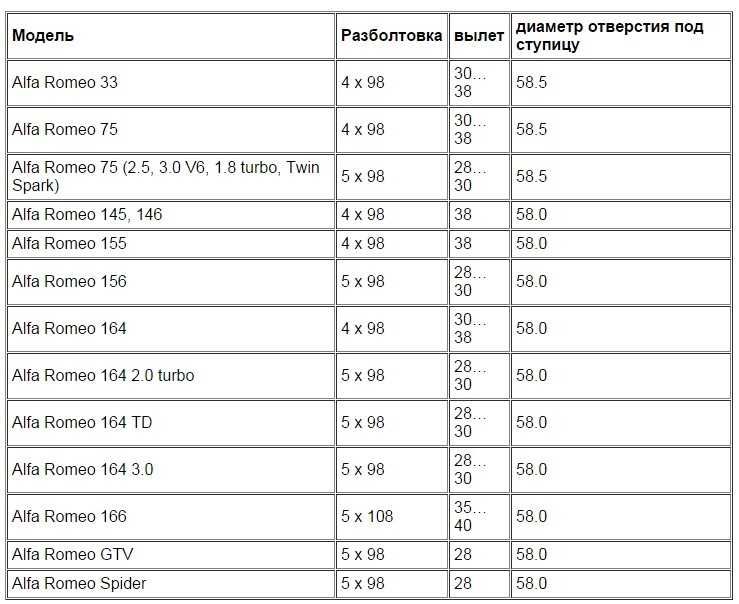
что это и для чего проводится?
Каждый водитель желает придать индивидуальность своему автомобилю. Наиболее эффективный способ – заменить стандартные скучные колесные диски на новые, различных именных брендов с выраженным рисунком и большим размером, которые существенно влияют на общий вид автомобиля. Но при подборе данной запчасти нужно учитывать технические характеристики конкретного транспортного средства, а также ряд других важных параметров, например, разболтовку. От разболтовки напрямую зависит правильность и безопасность установки автомобильного диска, поэтому следует рассмотреть параметр более детально.
Виды колесных дисков
Крепежные элементы разделяются на несколько видов в зависимости от разновидности колесного диска. Н современном рынке есть три основных вида колесных дисков: штампованные (стальные), литые (легко сплавные), кованые. Каждый тип обладает уникальными качествами и особенностями, поэтому следует ознакомиться с ними более детально:
- Штампованные диски более распространены, так как в основном являются базовой комплектующей частью автомобиля.
 У них доступная стоимость и высокая надежность. Штамповка легко поддается ремонту в результате механического повреждения, например, после удара об бордюр, попадания в глубокую яму или износа крепежных отверстий. Возможность рихтовать, сваривать и прокатывать привлекает практичных людей. К штампованным изделиям применимы все виды разболтовок.
У них доступная стоимость и высокая надежность. Штамповка легко поддается ремонту в результате механического повреждения, например, после удара об бордюр, попадания в глубокую яму или износа крепежных отверстий. Возможность рихтовать, сваривать и прокатывать привлекает практичных людей. К штампованным изделиям применимы все виды разболтовок. - Литые диски обладают меньшим весом и оригинальным внешним видом, нежели их штампованные аналоги. Такие диски очень тяжело восстановить, а зачастую даже невозможно, в связи с тем, что они подвержены растрескиванию при попадании в яму либо появлению осевого биения при боковых ударах. Потому что требуются дорогостоящие сварочные аргонно-дуговые и токарные работы. «Литье» имеет свои нормативы и таблицу с перечнем существующих разболтовок изделий, с которыми необходимо свериться при подборе колес для своей машины.
- Кованые диски обладают большим модельным рядом и разнообразным дизайном, а полюбились автомобилистами за их высокую надежность.
 Они имеют хорошую жесткость, достаточную прочность и коррозионную стойкость. Чтобы оставить вмятину на этом изделии нужно сильно «потрудиться», но все же ее можно устранить путем проката. Единственный минус данного изделия – цена. Производятся зачастую под заказ, поэтому возможно изготовление с любой разболтовкой.
Они имеют хорошую жесткость, достаточную прочность и коррозионную стойкость. Чтобы оставить вмятину на этом изделии нужно сильно «потрудиться», но все же ее можно устранить путем проката. Единственный минус данного изделия – цена. Производятся зачастую под заказ, поэтому возможно изготовление с любой разболтовкой.
Из-за конструктивных особенностей литых и кованых дисков при замене стандартных штампованных необходимо докупить крепежные болты, имеющие чуть большую длину, нежели стандартные. Для этого, в первую очередь, нужно понять, что такое разболтовка и как она выполняется.
Что же такое разболтовка колесных дисков?
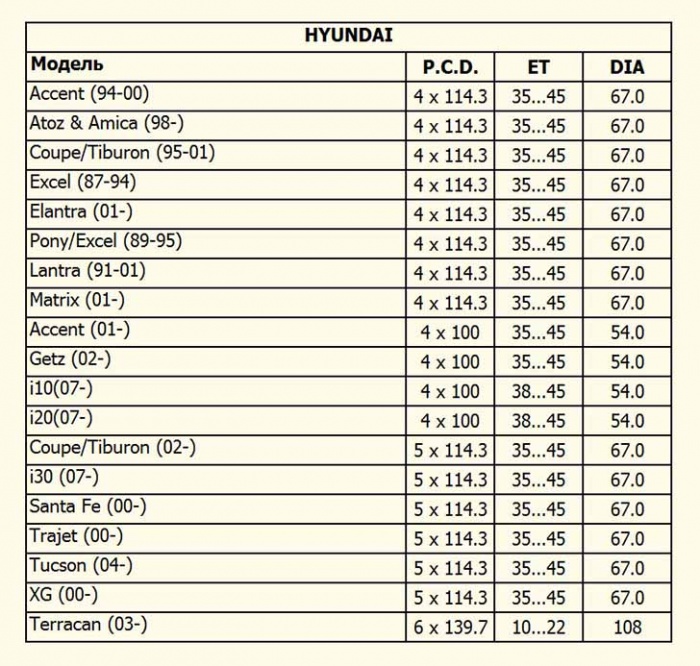
Разболтовка колесных дисков – основной параметр, на который нужно обратить внимание, он имеет обозначение PCD. Данное обозначение нанесено на сам диск и несет в себе информацию о количестве крепежных болтов на колесе и диаметр, по которому разнесены отверстия под крепление (сверловка). Неправильный подбор не даст установить колесо или может являться причиной среза крепежных болтов, а также потери колеса при движении транспортного средства.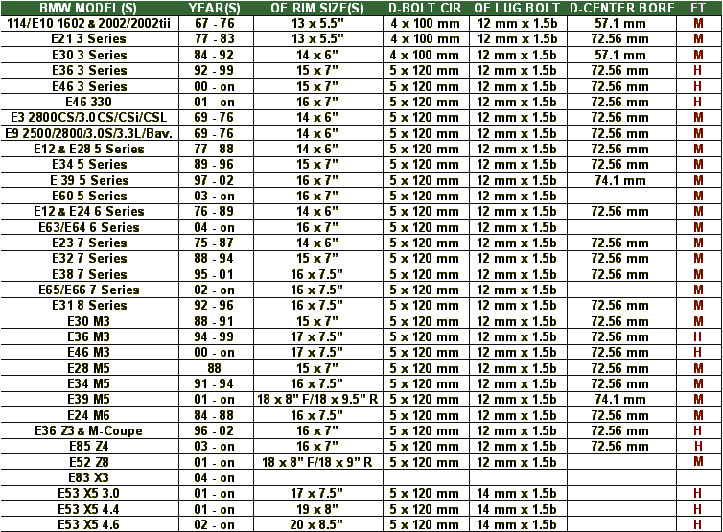
Сверловка зависит от марки, модели автомобиля, года изготовления и мощности двигателя. Имея все параметры, значение PCD выбирается по специальной таблице по международному стандарту или замеряется самостоятельно. Главное значение, которое нас интересует это количество крепежных болтов и сверловка. Рассмотрим несколько примеров таких значений: 4х98, 5х98, 4х108, 5х112, 5х115 и т.д.
Число в начале обозначает количество отверстий под крепление колеса, следующее обозначение является диаметром сверловки, то есть это окружность, которая проходит через центр отверстий, в них вставляются крепежные болты или шпильки. Если маркировка затерта на диске, то количество отверстий можно просто посчитать, а разболтовку промерить линейкой между центрами крепежных отверстий по диагонали. Данные параметры указаны в миллиметрах.
Далее измеряем центральное отверстие (DIA) штангенциркулем, а еще его можно узнать из технического руководства к конкретному транспортному средству. Служит оно для отцентровки колеса относительно ступицы автомобиля и предотвращает радиальное смещение относительно оси.
Немаловажный параметр – это вылет колеса (ЕТ), значение в миллиметрах. Существенное несоответствие с техническими требованиями к автомобилю приведет к затиранию колеса, как о кузов при повороте, так и об элементы подвески. Ширина диска (J), обозначается в дюймах и всего на 20-30% меньше ширины покрышки, делается это для того, чтобы защитить диск от повреждений из-за случайного касания колеса с боковым препятствием (например, бордюром). Сразу после данного параметра через значок «х» обозначен радиус обода колеса, на него монтируется покрышка, значение так же указано в дюймах.
Размеры и параметры дисков – это основной приоритет, который стоит учитывать при покупке и игнорировать его не стоит, а уже дизайн, модель и цвет несут второстепенное значение. Правильно подобранные диски напрямую влияют на безопасность эксплуатацию транспортного средства. При выполнении разболтовки нужно выполнить ряд подготовительных мероприятий, а еще лучше проконсультироваться со специалистом.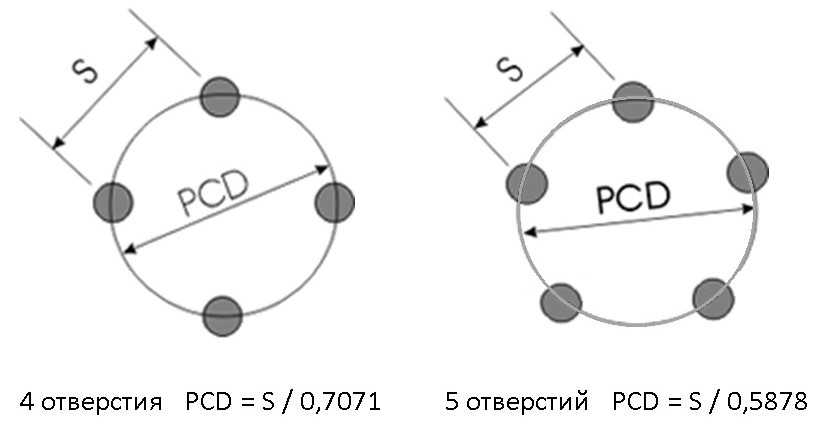
Разболтовка колесных дисков — обзорная статья
Планируете установить литье или просто осуществить сезонную смену колес на своем автомобиле? – Обязательно принимайте во внимание разболтовку! А почему это так важно, что включает в себя данный параметр и, вообще, что такое разболтовка колесных дисков, узнаете ниже.
Разболтовка дисков – это диаметр отверстий, предназначенных для болтов крепления колеса, а также количество этих самых отверстий. Диаметр в маркировке обозначают аббревиатурой PCD, а количество имеющихся на нем отверстий – LZ.
Всем тем, кто далек от знаний о строении и особенностях работы автомобилей, может казаться, что этот параметр носит информационный характер и заменить одно колесо на другое (например, штатное на более красивое широкопрофильное) – простая задача, лишь бы болты помещались в имеющиеся «дырки». Однако на деле это далеко не так: отступление от требований производителя в вопросах разболтовки чревато разбитой подвеской и разрушенным рулевым механизмом, и это в лучшем случае, в худшем – из-за некачественной протяжки колесо может просто открутиться в процессе движения, подвергнув жизнь водителя и его пассажиров большой опасности.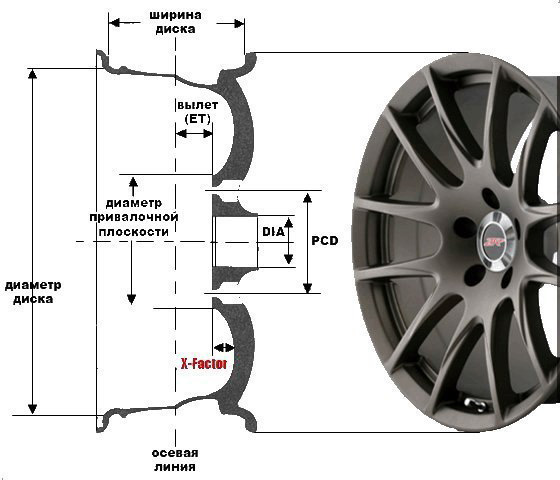 Поэтому рассмотрим не просто обозначение разболтовки, а место ее расположения в маркировке диска, используемые для этого символы, их значение, а также прочую информацию, которая не менее важна и может вам пригодиться.
Поэтому рассмотрим не просто обозначение разболтовки, а место ее расположения в маркировке диска, используемые для этого символы, их значение, а также прочую информацию, которая не менее важна и может вам пригодиться.
Итак, предположим, у вас есть диск, на который нанесена следующая информация: 7.5 Jx16 Н2 5/112 ET 35 d 58.5. Назовем каждое из имеющихся буквенно-цифровых обозначений. На изображении немного другой пример, однако смысл один и тот же.
Первая тройка, 7.5 Jx16, информирует, что ширина обода (W) данного диска составляет 7,5 дюймов (обратите внимание, именно в дюймах приводятся практически все параметры дисков, для справки: 1 дюйм = 2,54 см), диаметр (D) – 16 дюймов, а также, что представленный диск является неразъемным/не штампованным («х» – значок кованных и литых дисков).
Буква J в данном наборе присутствует также не просто так. Она указывает на предназначенность краев обода для моноприводных автомобилей, поэтому если, например, ваш автомобиль полноприводный – рассматриваемые диски ему не подходят, нужно поискать идентичные, но с немного другой маркировкой – JJ.
Обозначение Н2 несет информацию больше для специалистов и говорит о том, что на ободе присутствуют 2 кольцевых выступа (хампа), необходимые для удерживания бескамерной резины от соскальзывания. Естественно, если такой выступ будет только 1, на маркировке это обязательно будет отмечено, как Н1. Не исключено также полное отсутствие данных выступов или присутствие их, но в особой конструкции, тогда символы будут немного другие (АН, СН, FH). Так или иначе, рядовому автомобилисту этому параметру можно уделять наименьшее внимание, что нельзя сказать про следующие числа.
5/112 (на картинке 5/100) – и есть та самая разболтовка, которую мы рассматриваем в данной статье. 5 – число посадочных болтов и, соответственно, отверстий под них, 112 – диаметр окружности, на которой данные отверстия находятся, причем измеряется он уже не в дюймах, а в привычных для русского человека миллиметрах. Узнать разболтовку нужных вам дисков можно 3 способами, но об этом чуть позже, пока разберемся с оставшимися параметрами.
ET 35 – это вылет диска. В данном примере он равен 35 мм, вообще же вылет является расстоянием между плоскостью приложения диска к ступице и осью симметрии изделия. Если плоскость прижимания находится наравне с центром диска вылет называют нулевым, если выступает за его пределы – отрицательным, а если, наоборот, центр диска находится к ступице ближе плоскости приложения диска, как в примере, то про вылет говорят, что он положительный.
d 58.5 – диаметр центрального отверстия. Если он не совпадает с размером посадочного цилиндра на ступице машины, искать новые диски совсем необязательно, можно просто дополнительно приобрести комплект проставочных колец и с их помощью осуществить подгонку названных элементов друг под друга.
Как узнать разболтовку колес?
Как уже отмечалось ранее, сделать это можно 3-мя способами.
Способ №1 – обратиться в автосалон дилера или официальную станцию технического обслуживания, там можно получить всю необходимую информацию.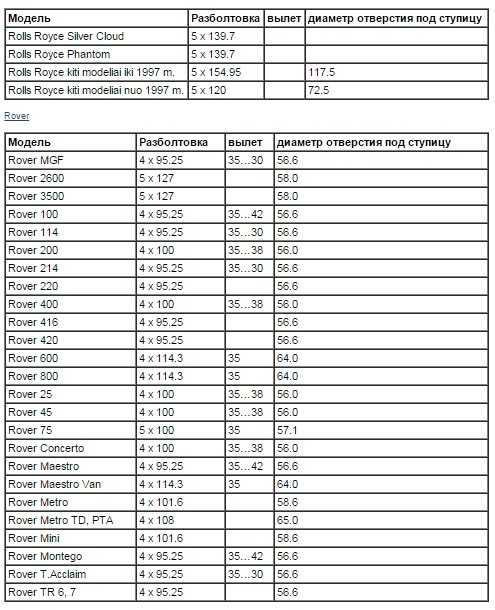
Способ №2 – рассчитать разболтовку самостоятельно.
Что для этого нужно сделать?
- Посчитать количество болтов.
- С помощью штангенциркуля измерьте расстояние между стенками соседних отверстий диска, прибавьте к нему их диаметр. В результате вы получите расстояние между центрами рядом расположенных отверстий, на рисунке оно обозначено «Х».
- Исходя из этого расстояния, определить PCD (разболтовку), для этого нужно умножить имеющийся у нас «Х» (на картинке N) на:
- 1,55, если LZ=3;
- 1,414, если LZ=4;
- 1,701, если LZ=5.
Если после всех произведенных вычислений вы получите дробное число, то округлять его следует в большую сторону. Но будьте внимательны, иногда производители не используют некоторые размеры разболтовок, например, Мерседес не допускает использование дисков с разболтовкой 111, поэтому если в ваших расчетах он получился именно таким, то выбирать следует маркировку 112.
Способ №3 – не тратить время зря, а сразу воспользоваться таблицей разболтовки колесных дисков.
Разболтовка колесных дисков: таблица совместимости.
Рекомендую прочитать:
Слово для защитного диска между винтом/болтом и материалом?
спросил
Изменено 5 лет, 1 месяц назад
Просмотрено 1к раз
Я пытаюсь заказать товар через Интернет, но ничего не могу найти. Так что у меня есть ощущение, что может быть слово, которое я пропускаю.
Я ищу название часто круглого диска, используемого для увеличения площади между винтом или болтом и материалом, в который он вставлен.
В частности, я ищу круглый металлический вариант диаметром 50 мм и толщиной 10 мм, если это имеет значение для названия.
В поисках металлических дисков, даже соответствующих размеров, я могу найти только шлифовальные и отрезные диски или другие виды инструментов.
- однословные запросы
0
Если вы говорите об одном из них, то я никогда не использовал ничего, кроме
1а. Перфорированный кольцевой диск или уплощенное кольцо из металла, кожи или другой материал, помещенный между двумя поверхностями, подверженными вращательному трение, чтобы уменьшить трение и предотвратить боковое движение и неустойчивость.
1346 Сч. Казначейство King’s Remembrancer 470/17 м. 2 Дэ..в Cheynes pro barr[a] continentibus L. Linches, v. paribus tenellarum, иж. Шайбы [и др.].
1544 на лат.
& Бумаги Генрих VIII XIX. я. 148 Запасные колеса для малый ordynaunce 12 пар, lynce~pynnes, шайбы, [и т. д.].
1611 Дж. Флорио Новый мир слов королевы Анны Cércio di ferro, железный обруч, называемый среди артиллеристов шайбой, который служит для удержания железный штифт на конце акселя от ношения науэ.
1682 в ранней записи. Город Провиденс (Род-Айленд) (1894 г.) VI. 93
Jn ye Parlor 3 Тележки, ящики для белья и стиральная машина 00–01–00.1704 Дикт. Rusticum at Cart The Washers, будучи кольцами на концы оси.
1705 т.р. G. Guillet de Saint-Georges Gentleman’s Dict. II. у ступицы
Аналогично в каждом конце отверстия, через которые конец ступицы Экслетри идет, железное кольцо, называемое желающим, спасает дыру нефа от ношения слишком большой.1795 Гершель в Филос. Транс. (Royal Soc.) 85 371 На ключе быстро на С; с соответствующими шайбами между соединениями, чтобы обеспечить очень плавное движение.
1805 R. W. Dickson Pract. Агр. I. Фото xii Винты для каждого зуба через двойную рамку, разделенную железными шайбами для большей устойчивость.
1847 Р. Брэндон и Дж. А. Брэндон Анал. Готический архит. I. 102 закрывающее кольцо или дверная защелка .. [состоит из] плоской пластины или шайбы, крепится к внешней поверхности двери; ручка или кольцо; и шпиндель.
1872 О. В. Холмс Поэт за завтраком i Стиральная машина… делает свободная винтовая посадка.
1876 R. D. Blackmore Cripps xxvi Огромное разнообразие колес, как а также их многочисленные капризы виляния, в зависимости от состояния их шайбы.
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Нелинейные динамические характеристики дисково-болтового ротора с погрешностью положения окружных отверстий под болты0005
Отверстия под болты в сборочных дисках предназначены для ограничения окружного смещения болтов дисково-болтового ротора. Погрешность положения окружных болтовых отверстий создается в трехмерной модели болто-дискового ротора. Распределение неравномерного напряжения и деформации получено в соответствии с подходом конечных элементов. Статические результаты показывают, что ошибка положения болтовых отверстий приводит к очевидным сопутствующим дисбалансам, включая эксцентриситет постоянной массы и изменяющийся по скорости изгиб под действием большой силы затяжки. Когда эти факторы дисбаланса принимаются во внимание, динамические характеристики, такие как области нестабильности и нелинейные движения, анализируются с помощью итеративного процесса Ньютона и метода расчета прогнозирования-коррекции. Динамические результаты показывают, что изгиб ротора позволяет снизить систематическую устойчивость, очевидно, из-за этой ошибки положения. Существует особое явление по сравнению с моноблочным ротором, заключающееся в том, что амплитуда вибрации продолжает расти, когда скорость вращения превышает критическую скорость. Более того, допустимая погрешность положения отверстий под болты, очевидно, меньше, чем у моноблочного ротора, а неравномерная затяжка является реальным способом уменьшения неблагоприятного воздействия на динамические свойства при появлении погрешности положения. В этой работе предлагается статодинамический подход к исследованию динамики неточного дисково-болтового ротора и устанавливается взаимосвязь между погрешностью обработки и динамическими характеристиками.
Динамические результаты показывают, что изгиб ротора позволяет снизить систематическую устойчивость, очевидно, из-за этой ошибки положения. Существует особое явление по сравнению с моноблочным ротором, заключающееся в том, что амплитуда вибрации продолжает расти, когда скорость вращения превышает критическую скорость. Более того, допустимая погрешность положения отверстий под болты, очевидно, меньше, чем у моноблочного ротора, а неравномерная затяжка является реальным способом уменьшения неблагоприятного воздействия на динамические свойства при появлении погрешности положения. В этой работе предлагается статодинамический подход к исследованию динамики неточного дисково-болтового ротора и устанавливается взаимосвязь между погрешностью обработки и динамическими характеристиками.
1. Введение
Диско-болтовой ротор представляет собой типичный комбинированный ротор, в котором множество отдельных частей, таких как диски, скреплены между собой одним центральным болтом или несколькими болтами, распределенными по окружности.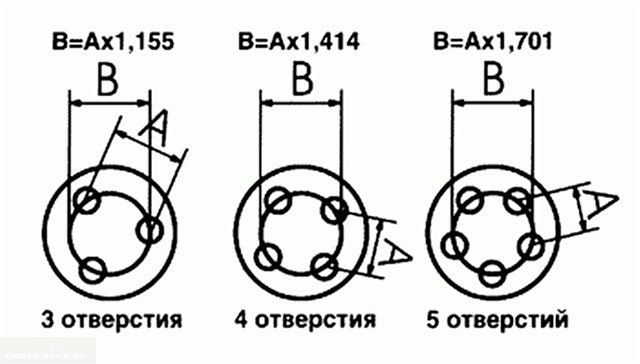 Такая конструкция ротора имеет широкое применение в газовых турбинах, авиационных двигателях и т.д. Отверстия под болты в сборочных дисках предназначены для ограничения смещения болтов по окружности. Чтобы удовлетворить высокие требования к сборке, отверстия под болты изготавливаются очень точно перед сборкой дисков. Например, погрешность положения отверстий под болты в 17 сборочных дисках ротора газовой турбины F-класса (рис. 1) поддерживается на уровне менее 50 µ м при распределенном диаметре болтов 980 мм. Почему точность положения болтовых отверстий в болто-дисковом роторе такая высокая? В этой статье эта основная проблема будет обсуждаться с точки зрения трехмерной нелинейной динамики ротора.
Такая конструкция ротора имеет широкое применение в газовых турбинах, авиационных двигателях и т.д. Отверстия под болты в сборочных дисках предназначены для ограничения смещения болтов по окружности. Чтобы удовлетворить высокие требования к сборке, отверстия под болты изготавливаются очень точно перед сборкой дисков. Например, погрешность положения отверстий под болты в 17 сборочных дисках ротора газовой турбины F-класса (рис. 1) поддерживается на уровне менее 50 µ м при распределенном диаметре болтов 980 мм. Почему точность положения болтовых отверстий в болто-дисковом роторе такая высокая? В этой статье эта основная проблема будет обсуждаться с точки зрения трехмерной нелинейной динамики ротора.
Для традиционных исследований роторной динамики модели ротора обычно рассматриваются как жесткий ротор, ротор Джеффкотта, одномерный ротор с конечными элементами (например, ротор с балкой Тимошенко) и т. д. [1–5]. Эти модели очень классические и полезны для анализа основных динамических свойств, но детализированные особенности (такие как отверстия и дефекты) в роторе не могут быть отражены полностью, потому что в этих базовых моделях ротора неизбежно присутствует упрощение конструкции. Чтобы описать фактическое влияние погрешностей обработки, модель болтового диска ротора должна быть создана в трехмерном виде, который может содержать все структурные особенности ошибки положения отверстий под болты. Для реальных нужд техники представлен одномерный болто-дисковый ротор [6], но трехмерные динамические эффекты болто-дискового ротора не могут быть учтены в комбинированной модели. Впоследствии для получения характеристик моноблочного ротора предлагается подход трехмерного нелинейного роторно-динамического анализа [7].
Чтобы описать фактическое влияние погрешностей обработки, модель болтового диска ротора должна быть создана в трехмерном виде, который может содержать все структурные особенности ошибки положения отверстий под болты. Для реальных нужд техники представлен одномерный болто-дисковый ротор [6], но трехмерные динамические эффекты болто-дискового ротора не могут быть учтены в комбинированной модели. Впоследствии для получения характеристик моноблочного ротора предлагается подход трехмерного нелинейного роторно-динамического анализа [7].
Однако ошибка положения болтовых отверстий вызывает смешанную статическую и динамическую проблему, поскольку равномерно распределенное усилие затяжки болтов может привести к заметной деформации. Существует отчет [8], в котором рассматривается только шероховатость интерфейсов по этой проблеме статико-динамического объединения, но этот метод не подходит для анализа ошибки позиционирования, поскольку она имеет больший масштаб формы и будет вызывать более очевидные эффекты, чем шероховатость поверхности.
В этой статье рассматривается ошибка фактического положения болтовых отверстий в трехмерной модели болтового диска ротора. Метод конечных элементов, включая контактный расчет [9, 10] принято для анализа статических воздействий. Последующие трехмерные динамические свойства ротора, такие как устойчивость и вибрация, получаются с помощью итеративного процесса Ньютона, метода прогнозирования-коррекции и теории Флоке [11–14]. Сравнение болтового диска и моноблочного ротора также широко обсуждается, чтобы сделать относительные выводы.
2. Статические характеристики неточного дисково-болтового ротора с ошибкой позиционирования отверстий под болты
2.1. Конструкция подшипниковой системы болт-диск ротора
Взяв за основу базовую конструкцию компрессора ротора газовой турбины класса F (рис. 1), аналогичный болт-дисковый ротор будет изучен на рис. 2. Этот комбинированный ротор имеет три отдельных диска («a», «b»). », и «с»), которые закреплены несколькими расположенными по окружности болтами, которые проходят через отверстия в дисках (зеленые линии на рисунке 2 и называются отверстиями для болтов). Каждый болт имеет одинаковый размер и удлинение, которое крепится для затягивания каждого вращающегося диска этого ротора.
Каждый болт имеет одинаковый размер и удлинение, которое крепится для затягивания каждого вращающегося диска этого ротора.
Во время сборки болт-диск ротора совмещают вертикально, чтобы избежать влияния силы тяжести. Интерфейсы осевой сборки (синие линии) между тремя дисками используются для обеспечения достаточной контактной жесткости. Концентричность между дисками гарантируется некоторыми соосно расположенными интерфейсами (красные линии). Поверхности болтов спроектированы таким образом, чтобы соответствовать боковым поверхностям соответствующих отверстий в дисках.
После описанного выше регламентированного процесса сборки дисково-болтовой ротор устанавливается горизонтально и поддерживается двумя цилиндрическими подшипниками скольжения («j» и «k»). Скорость вращения варьируется от 0 до 7500 об/мин (рабочая скорость). В таблице 1 показаны переменные болтового диска ротора и подшипника.
2.2. Погрешность положения болтовых отверстий
Погрешность положения кольцевых отверстий под болты в этом документе показана на рис. 3(а). Из-за этой позиционной ошибки центр распределенных по окружности болтовых отверстий на диске «b» смещается с O (идеальное положение) на O ’ (фактическое положение). Отклонение ч = | ОО ’| составляет 50 μ м по сравнению с ротором газовой турбины F-класса. Между тем, два других диска изготовлены идеально.
3(а). Из-за этой позиционной ошибки центр распределенных по окружности болтовых отверстий на диске «b» смещается с O (идеальное положение) на O ’ (фактическое положение). Отклонение ч = | ОО ’| составляет 50 μ м по сравнению с ротором газовой турбины F-класса. Между тем, два других диска изготовлены идеально.
Неточный диск 3D и соответствующий дисково-болтовой ротор дискретизированы на м узловых ( м = 8) элементов с применением метода конечных элементов, которые показаны на рисунке 3(b).
2.3. Статический анализ
Ключевым моментом статического анализа является расчет напряжения и состояния контактных поверхностей в болт-дисковом роторе, полученных итерацией [10]:где K R — матрица жесткости болто-дисковый ротор; u – вектор смещения; η — множитель Лагранжа; h — контактные ограничения; F — вектор силы; Λ – штрафной коэффициент; and K Λ = H T Λ H and F Λ = H T Λ h 0 in which H = ∂ ч /∂ и .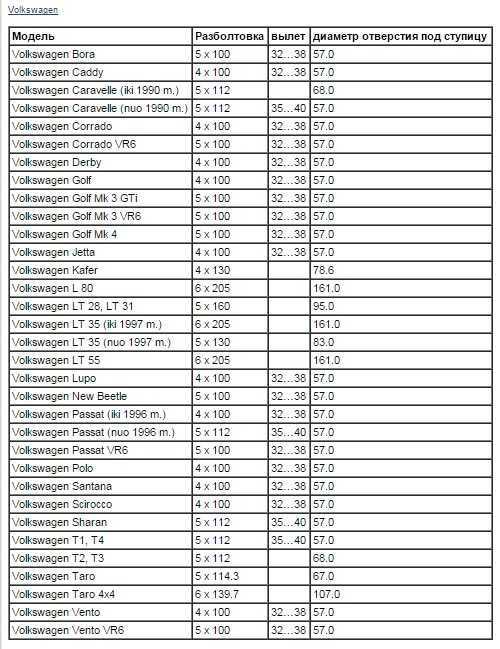
Поскольку условия ограничений постоянно меняются в зависимости от состояния контакта, для решения приведенных выше уравнений используется пошаговая итерация.
Для сравнения проводится статический анализ для изучения относительных характеристик идеального и неточного болтово-дискового ротора. На Рисунке 4 при постоянной скорости (7500 об/мин) результаты показывают, что напряжение болта (например, болта № 4) в идеальном болтово-дисковом роторе распределяется равномерно. Однако в неточном болтово-дисковом роторе на соответствующий болт возникает заведомо неравномерное напряжение.
Из-за ошибки положения отверстий под болты поверхности отверстий под болты диска «b» сжимают несколько болтов, когда диск смещается в поперечном направлении после сборки. В результате неоднородное напряжение и деформация изгиба вызваны усилием прессования.
Следовательно, ошибка положения болтовых отверстий приводит к эксцентриситету массы e ; неравномерное напряжение вызывает смещение центра оси с d . По сравнению с ротором для точной обработки ошибка положения на диске «b» вызывает постоянную величину e (равную 2,98 μ м) в течение всей процедуры и изменение скорости с d в рабочий процесс, который постепенно увеличивается до 6,28 μ м при рабочей скорости (7500 об/мин).
По сравнению с ротором для точной обработки ошибка положения на диске «b» вызывает постоянную величину e (равную 2,98 μ м) в течение всей процедуры и изменение скорости с d в рабочий процесс, который постепенно увеличивается до 6,28 μ м при рабочей скорости (7500 об/мин).
С другой стороны, s d и e точного диска чрезвычайно близки к нулю. Это доказывает, что точность расчета абсолютно достаточна для анализа статических влияний погрешности положения болтовых отверстий в роторе.
Затем смещение центра диска s d позволяет комбинированному ротору иметь полный изгиб r d , вектор которого определяется как r 0153 D = ( S 1 ,…, S D ,…, S K 4), в котором IS AS AS AS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS .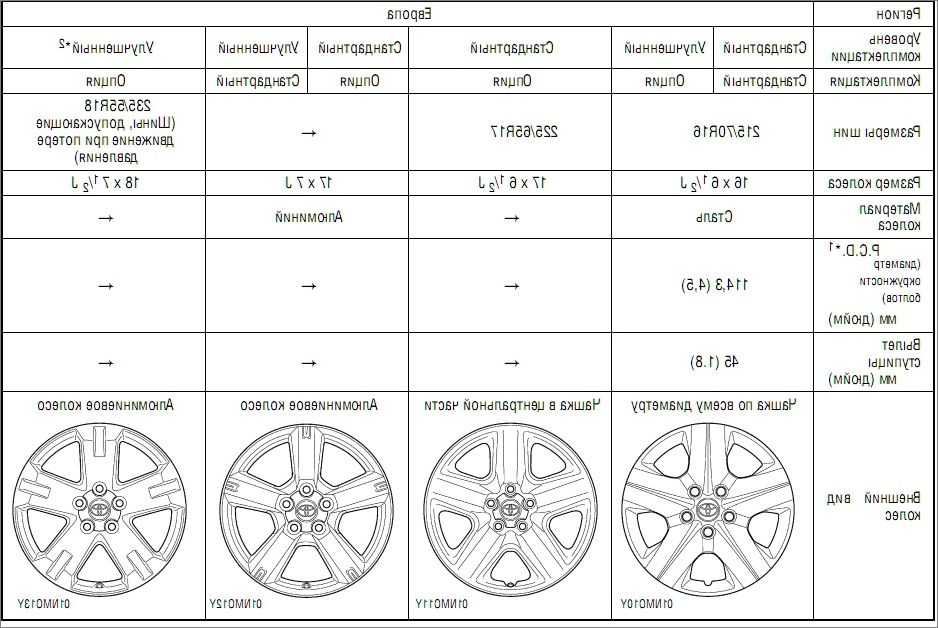 5). Способ получения s k аналогичен вычислению s d . Изгиб ротора происходит в процессе сборки, а в рабочем процессе он усиливается за счет центробежной тяги. Изменение изгиба абсолютно не существует в традиционном моноблочном роторе, который не имеет кольцевых болтов и усилия затяжки.
5). Способ получения s k аналогичен вычислению s d . Изгиб ротора происходит в процессе сборки, а в рабочем процессе он усиливается за счет центробежной тяги. Изменение изгиба абсолютно не существует в традиционном моноблочном роторе, который не имеет кольцевых болтов и усилия затяжки.
3. Динамические уравнения и нелинейный метод решения
3.1. Уравнения трехмерного неточного ротора и редукции системы
Когда диско-болтовой ротор имеет коэффициент дисбаланса, включающий эксцентриситет массы и изгиб ротора, динамическая модель неточной системы ротора с болтовым диском должна их учитывать.
Для трехмерной системы болт-диск ротора степени свободы делятся на нелинейные и линейные составляющие. Степени свободы относятся к узлам подшипников (используются для добавления сил подшипника), а узлы дисков (используются для добавления сил дисбаланса) определяются как нелинейные компоненты; все остальные степени свободы, принадлежащие другим узлам ротора, определяются как линейная составляющая.
Для нелинейной составляющей собственные моды могут отражать динамические характеристики линейной системы. В результате вычисляются собственные значения уравнений в линейной составляющей и резервируются первые несколько собственных мод.
Затем уравнения динамики делятся на линейные и нелинейные участки: где M R и G R – матрица масс и матрица гироскопа ротора; г — вектор силы тяжести; нижние индексы «a» и «i» обозначают нелинейную и линейную степени свободы соответственно; и f B – вектор опорных сил, который рассчитывается на основе метода конечных разностей [15]. Подушечка цилиндрического подшипника по геометрии дискретизирована на множество узлов. Полная опорная сила рассматривается как сумма гидродинамических давлений, которая решается уравнением Рейнольдса.
Кроме того, линейные степени свободы динамического уравнения (2) редуцированы матрицей преобразования T с применением метода синтеза компонентных мод [16]. В результате остаточные уравнения неточной роторной системы записываются как with.
В результате остаточные уравнения неточной роторной системы записываются как with.
Для уменьшенной системы болт-диск ротора, показанной на рис. 3(b), зарезервированные степени свободы равны 27, включая 3 дисковых узла (9 степеней свободы), 2 опорных узла (6 степеней свободы) и собственные формы первых 12 порядков (6 жестких собственных форм). и 6 упругих собственных мод).
3.2. Метод нелинейного решения
Чтобы получить перемещение и скорость, вводится параметр состояния Y : где и λ — переменная возбуждения, такая как ω , e и r д .
Поскольку e и r d удовлетворяют периодическому признаку при вращении ротора, решения уравнения (4) определяются выражением где T – период вращения.
При λ = λ 0 уравнение (4) можно преобразовать в решение целевых периодических решений Y ( t ) согласно нелинейному определению
Y ( т ).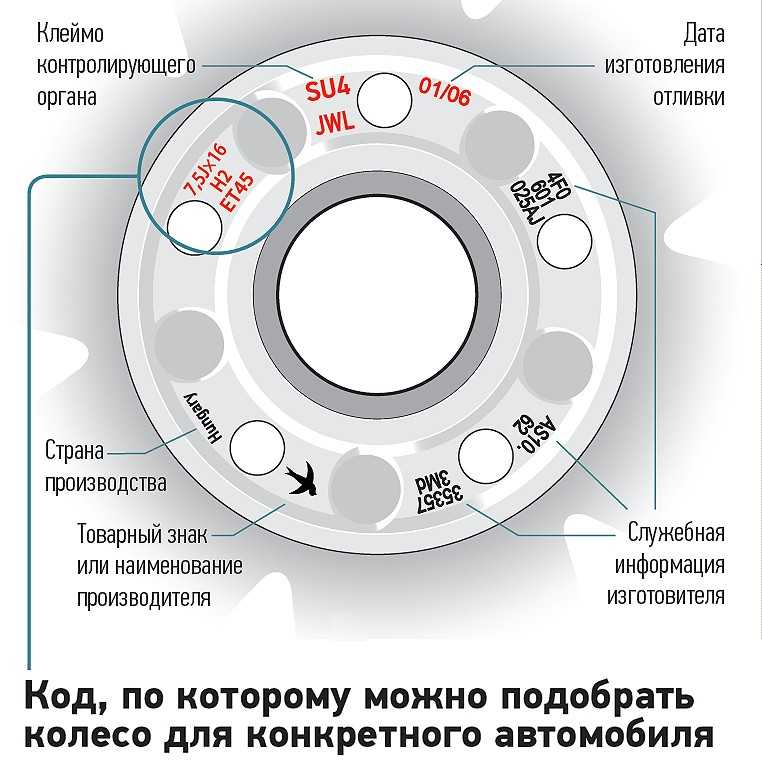 H ( λ 0 , Y ) определяется по начальному значению Y 0 и Jacobian Matrix ∂ H /∂ y ( /∂ y ( /∂ y . в (6), Y вычисляется в соответствии со следующей итерацией Ньютона:0095 λ меняется, уравнение (6) заменяется на H ( λ , Y ) = 0 . Если n раствор забега y N Решен, N +1 Supe начинается с Modewhere прогнозирования ∂ H ( λ , Y 8) ( λ , y 8) ( λ , y 8). интегрирование уравнения (11): с (∂ Y /∂ λ ) t 0 = 0 и (∂ Y /∂ λ ) ( t 0+ T ) = ∂ H ( λ , Y )/∂ 909095 .
H ( λ 0 , Y ) определяется по начальному значению Y 0 и Jacobian Matrix ∂ H /∂ y ( /∂ y ( /∂ y . в (6), Y вычисляется в соответствии со следующей итерацией Ньютона:0095 λ меняется, уравнение (6) заменяется на H ( λ , Y ) = 0 . Если n раствор забега y N Решен, N +1 Supe начинается с Modewhere прогнозирования ∂ H ( λ , Y 8) ( λ , y 8) ( λ , y 8). интегрирование уравнения (11): с (∂ Y /∂ λ ) t 0 = 0 и (∂ Y /∂ λ ) ( t 0+ T ) = ∂ H ( λ , Y )/∂ 909095 .
Он заканчивается следующей итерацией коррекции, основанной на уравнении (8) для решения Y n +1 :
Моноблочный ротор того же размера анализируется одновременно.
 Радиально расположенные болты моноблочного ротора не имеют удлинения, а все диски склеены между собой. Моноблочный ротор имеет такой же эксцентриситет массы, что и ротор с болтовым соединением, но не имеет деформации изгиба, поскольку для этого ротора не предусмотрена процедура сборки.
Радиально расположенные болты моноблочного ротора не имеют удлинения, а все диски склеены между собой. Моноблочный ротор имеет такой же эксцентриситет массы, что и ротор с болтовым соединением, но не имеет деформации изгиба, поскольку для этого ротора не предусмотрена процедура сборки.4.1. Устойчивость и бифуркация неточной системы болт-диск
Границы общей устойчивости и зоны неточной системы болт-диск и моноблочного ротора показаны на рис. 6.
Границы общей устойчивости определяются собственными значениями (множителями Флоке) Матрица Якоби ∂ H /∂ Y в уравнении (7) в работе [11–14]. Для устойчивого периодического решения все множители Флоке должны находиться в пределах единичного круга на комплексной плоскости. Наибольшая величина среди всех собственных значений матрицы называется старшим множителем Флоке. Как правило, обычная двойная периодичность возникает, когда реальный ведущий множитель Флоке пересекает единичный круг на отрицательной действительной оси. Кроме того, квазипериодическая бифуркация произойдет, когда пара комплексно-сопряженных старших множителей Флоке пересечет единичную окружность.
Кроме того, квазипериодическая бифуркация произойдет, когда пара комплексно-сопряженных старших множителей Флоке пересечет единичную окружность.
B 1 и B 2 обозначают границы квазипериодического (QP) и двойного периодического (DP) решения для неточной системы болт-диск ротора. B’ 1 и B’ 2 означают границы QP и DP для моноблочной роторной системы. P представляет область периодического решения, в которой роторная система имеет устойчивые периодические орбиты. Области глобальной устойчивости систем болтового диска и моноблочного ротора состоят из трех частей: области P, QP и DP.
Кривая ( e + r d ) and line ( e ) are extracted from the results of Figure 7. Curve ( e + r d ) and B 1 have a crossing точка ; линия ( e ) и B’ 1 имеют точку пересечения. Если ω < (), болто-дисковый (моноблочный) ротор будет совершать P движений; если ω > (), болто-дисковый (моноблочный) ротор совершает QP-движения.
Можно заметить, что площадь P дисково-болтового ротора явно меньше, чем у моноблочного ротора. Это означает, что изгиб ротора из-за ошибки положения болтовых отверстий имеет меньшую устойчивость системы.
4.2. Нелинейная вибрация
Вибрация на рис. 8(a) указывает на то, что обе роторные системы имеют почти одинаковую критическую скорость ( ω c ≈ 4800 об/мин), но ее амплитуда A c болта-диска 9015 ротор больше, чем у моноблочного ротора. Таким образом, изгиб ротора в зависимости от скорости практически не влияет на критическую скорость, но может вызвать большую вибрацию. Отличительной особенностью здесь является неточный болт-диск ротора. Перед балансом амплитуда снова возрастает, когда ω > ω с ; После баланса (скорость баланса равна ω C ), вибрация также увеличивается и становится больше критической амплитуды A C , когда ω > ω
Эти характеристики также проявляются в вибрационной реакции ротора газовой турбины (рис. 1), который также является типичным ротором с болтовым соединением. Данные на рис. 8(b) получены в процессе динамической балансировки, на который не влияют газ и тепло. Датчики смещения используются для измерения вибрации вала. На определенной скорости ротор останавливается на несколько минут, чтобы определить уровень вибрации. Точно так же, независимо от того, имеет ли ротор газовой турбины класса F динамическую уравновешенность (уравновешивающая скорость равна его второй критической скорости 2200 об / мин), вибрация снова возрастает через ω с .
Причина ясна при анализе вибрации неточного болтово-дискового ротора. Поскольку скорость баланса равна ω C , чтобы уменьшить его возбуждение F C , насколько это возможно, Balance Vector B C. Когда ротор имеет вектор баланса B c на критической скорости, амплитуда колебаний теоретически равна нулю, поскольку возбуждение полностью сбалансировано при ω = ω c .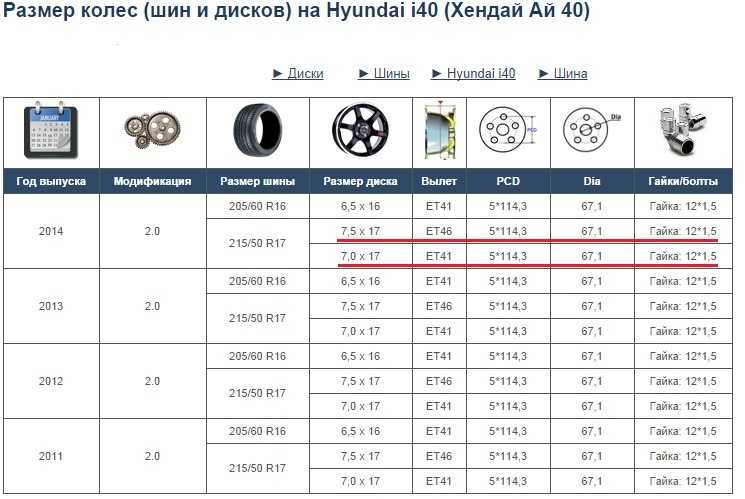 Однако для других скоростей ( ω ≠ ω C ) вектор возбуждения F переписывается как
Однако для других скоростей ( ω ≠ ω C ) вектор возбуждения F переписывается как
. . Кроме того, F становится больше по мере увеличения скорости, когда ω > ω c . Следовательно, амплитуда вибрации снова возрастает после критической скорости.
Это особое явление является причиной того, что погрешность положения болтовых отверстий в роторе очень востребована. Это также указывает на то, что эту ошибку обработки следует тщательно изучить при проектировании такого типа комбинированного ротора.
4.3. Нелинейные вибрационные характеристики неточных роторов
На рис. 6 показано, что неточные болт-дисковые и моноблочные подшипниковые системы теряют локальную устойчивость при 8170 об/мин и 7850 об/мин. На рисунках 9(а) и 9(б) показаны квазипериодические движения 13 узлов на оси ротора, а линия, соединяющая орбиты, представляет собой переходную моду колебаний деформированного ротора.
На рис. 10(a) сравниваются вихревые орбиты обоих неточных роторов в узле подшипника «k». Рисунок 10(b) показывает, что движения неточного ротора с болтовым диском и неточного моноблочного ротора обычно квазипериодичны, поскольку соответствующие точки Пуанкаре образуют замкнутую кривую.
Для получения частотных спектров неточных роторов выполняется быстрое преобразование Фурье (БПФ). На рисунке 11 показано, что обе системы имеют схожие частотные характеристики: частота гармоник, частота неустойчивости масляной пленки и высокие частоты.
Частота гармоник (136,1 Гц и 130,8 Гц) рассчитывается по скорости вращения; частота неустойчивости масляной пленки (74,87 Гц и 78,48 Гц) примерно равна половине частоты гармоники, которая возникает из периодического решения Хопфа уравновешенной роторной системы, и на ротор воздействует эффект колебаний масляной пленки; высокие частоты возникают из-за квазипериодического движения.
4.4. Допустимая ошибка положения
Неизменный эксцентриситет массы e и изгиб ротора с переменной скоростью r d в роторе с болтовым диском, когда между дисками существует ошибка положения отверстий под болты. Избыток e и r d отрицательно скажется на динамических характеристиках. Для эффективного контроля этих факторов необходимо обеспечить максимально допустимую погрешность.
Избыток e и r d отрицательно скажется на динамических характеристиках. Для эффективного контроля этих факторов необходимо обеспечить максимально допустимую погрешность.
Для диаграммы устойчивости (рисунок 12) неточного болтового диска и моноблочного ротора кривая ( E + R D ) и линия ( E ) постепенно приближается к их границам стабильности, когда E и R D 44. В этом диапазоне скоростей оба ротора должны все время работать в стабильной зоне (зона P). Таким образом, максимально допустимую ошибку позиционирования можно найти, когда кривая ( e + r d ) и линия ( e ) касаются границы B 2 и B’ 2 соответственно.
Результаты анализа показывают, что максимально допустимая погрешность положения болтовых отверстий для болтового диска и моноблочного ротора составляет 137 μ м и 417 μ м.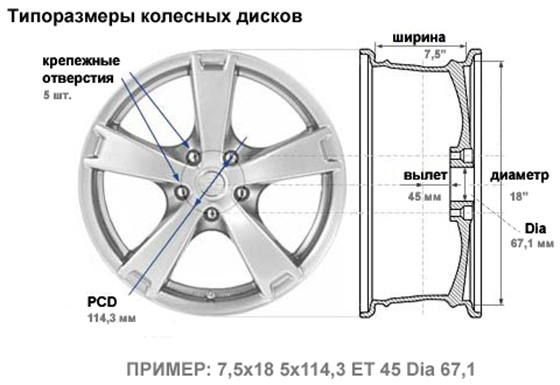 Этот допуск также указывает на точность положения болтов при проектировании этого комбинированного ротора.
Этот допуск также указывает на точность положения болтов при проектировании этого комбинированного ротора.
5. Выводы
В данной работе представлен статико-динамический объединенный анализ для изучения влияния погрешности положения болтовых отверстий в типичной системе болт-диск ротора. Выводы включают следующее: (1) Отклонение ошибки положения болтовых отверстий вызывает эксцентриситет массы и изгиб ротора из-за удлинения затяжки и рабочей скорости для неточного диска. (2) Составляющая дисбаланса, включая эксцентриситет массы и изгиб ротора, возникающие из-за ошибка положения отверстий под болты приводит к явному снижению устойчивости и увеличению вибрации. (3) Амплитуда вибрации неточного болт-дискового ротора снова возрастает при ω > ω c до (или после) динамического баланса. Это свойство также существует в роторе газовой турбины класса F и, очевидно, отличается от моноблочного ротора. (4) Допустимая погрешность положения отверстий под болты, очевидно, меньше, чем у моноблочного ротора. Это показывает, что эта точность сборки должна быть ограничена, чтобы максимально избежать ошибки позиционирования.
Это показывает, что эта точность сборки должна быть ограничена, чтобы максимально избежать ошибки позиционирования.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, включены в статью.
Конфликт интересов
Авторы заявляют, что у них нет конфликта интересов в отношении данной статьи.
Благодарности
Работа, описанная в этой статье, финансировалась за счет гранта Национального научного фонда Китая (№ 51705399) и Aeronautics Power Foundation (№ 6141B0).
Ссылки
К.-Б. Ли, Ю.-Б. Ким и К.-Ю. Чжон, «Идентификация параметра подшипника ротора с использованием данных об орбите»,
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Дж. Лу, Р. Дай, Д.
 Хей, Ю. Ф. Чжан, Х. Лю и Л. Ю, «Стабильность и бифуркация нелинейной динамической системы соединения подшипника и гибкого ротора», Труды Институт инженеров-механиков, часть C: Journal of Machine Engineering Science , vol. 223, нет. 4, стр. 835–849, 2009 г.
Хей, Ю. Ф. Чжан, Х. Лю и Л. Ю, «Стабильность и бифуркация нелинейной динамической системы соединения подшипника и гибкого ротора», Труды Институт инженеров-механиков, часть C: Journal of Machine Engineering Science , vol. 223, нет. 4, стр. 835–849, 2009 г.Посмотреть по адресу:
Сайт издателя | Академия Google
М. Ченг, Г. Мэн и Дж. П. Цзин, «Численное исследование системы ротор-подшипник-уплотнение», Труды Института инженеров-механиков, часть C: Журнал машиностроения
, том. 221, нет. 7, стр. 779–788, 2007.Посмотреть по адресу:
Сайт издателя | Google Scholar
J. Yi, H. Liu, F. T. Wang, M. Li, M. Jing, «Резонансный эффект, вызванный переменной податливой вибрацией для упругого ротора, поддерживаемого роликовыми подшипниками», Труды Института инженеров-механиков, часть C: J.
 Multi-Body Dynamics , vol. 228, нет. 4, стр. 779–788, 2014.
Multi-Body Dynamics , vol. 228, нет. 4, стр. 779–788, 2014.Посмотреть по адресу:
Сайт издателя | Google Scholar
Z. Wan, J.-P. Цзин, Г. Мэн, Ю. Ян и Х.-Ю. Бай, «Теоретическое и экспериментальное исследование динамической реакции многодисковой роторной системы с несоосностью гибкой муфты», Труды Института инженеров-механиков, часть C: Journal of Machine Engineering Science
Посмотреть по адресу:
Сайт издателя | Google Scholar
К. Юань, Дж. Гао и П. Ли, «Нелинейная динамика ротора Джеффкотта со стержневым креплением», ASME Journal of Applied Mechanics , vol. 136, с. 021011, 2014.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю.
 Лю, Х. Лю, Дж. И и М. К. Цзин, «Исследование устойчивости и бифуркации трехмерной системы ротор-подшипник», ASME Journal of Vibration and Acoustics , vol. 135, с. 031017, 2013.
Лю, Х. Лю, Дж. И и М. К. Цзин, «Исследование устойчивости и бифуркации трехмерной системы ротор-подшипник», ASME Journal of Vibration and Acoustics , vol. 135, с. 031017, 2013.Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Лю, Х. Лю, С. Ван и М. Цзин, «Нелинейные динамические характеристики трехмерной системы подшипника ротора с креплением стержня», Труды Института инженеров-механиков, часть C: Journal of Machine Engineering Science , vol. 229, нет. 5, стр. 882–894, 2015 г.
Посмотреть по адресу:
Сайт издателя | Академия Google
K. J. Bathe, Методы конечных элементов , Prentice-Hall, Хобокен, Нью-Джерси, США, 1996. , том. 2, нет. 4, стр. 1–49, 1995.
Посмотреть по адресу:
Сайт издателя | Google Scholar
П.
 Сундарараджан и С. Т. Ноа, «Динамика вынужденных нелинейных систем с использованием метода стрельбы/продолжения длины дуги — применение к роторным системам», Журнал вибрации и акустики , вып. 119, нет. 1, стр. 9–20, 1997.
Сундарараджан и С. Т. Ноа, «Динамика вынужденных нелинейных систем с использованием метода стрельбы/продолжения длины дуги — применение к роторным системам», Журнал вибрации и акустики , вып. 119, нет. 1, стр. 9–20, 1997.Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Х. Б. Фей, Д. Х. Ван Кампен и А. де Кракер, «Долгосрочная структурная динамика механических систем с локальными нелинейностями», Journal of Vibration and Acoustics , vol. 118, нет. 2, стр. 147–153, 1996.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Т. С. Паркер и Л. О. Чуа, Практические численные алгоритмы для хаотической системы , Springer-Verlag, New York, NY, USA, 1989.
R. Seydel, From Equilibrium to Chaos, Practical Bifurcation and Stability Analysis , Elsevier, New York, NY, USA, 1988.



 У них доступная стоимость и высокая надежность. Штамповка легко поддается ремонту в результате механического повреждения, например, после удара об бордюр, попадания в глубокую яму или износа крепежных отверстий. Возможность рихтовать, сваривать и прокатывать привлекает практичных людей. К штампованным изделиям применимы все виды разболтовок.
У них доступная стоимость и высокая надежность. Штамповка легко поддается ремонту в результате механического повреждения, например, после удара об бордюр, попадания в глубокую яму или износа крепежных отверстий. Возможность рихтовать, сваривать и прокатывать привлекает практичных людей. К штампованным изделиям применимы все виды разболтовок.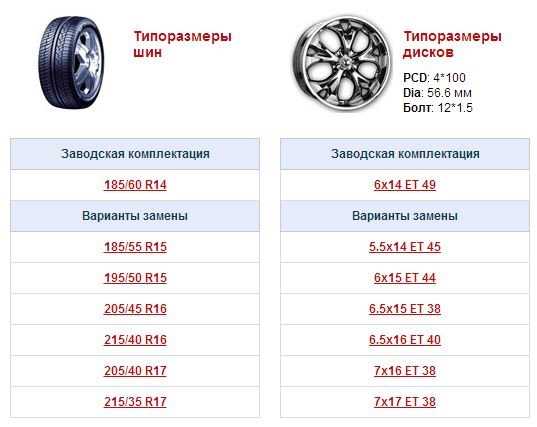 Они имеют хорошую жесткость, достаточную прочность и коррозионную стойкость. Чтобы оставить вмятину на этом изделии нужно сильно «потрудиться», но все же ее можно устранить путем проката. Единственный минус данного изделия – цена. Производятся зачастую под заказ, поэтому возможно изготовление с любой разболтовкой.
Они имеют хорошую жесткость, достаточную прочность и коррозионную стойкость. Чтобы оставить вмятину на этом изделии нужно сильно «потрудиться», но все же ее можно устранить путем проката. Единственный минус данного изделия – цена. Производятся зачастую под заказ, поэтому возможно изготовление с любой разболтовкой.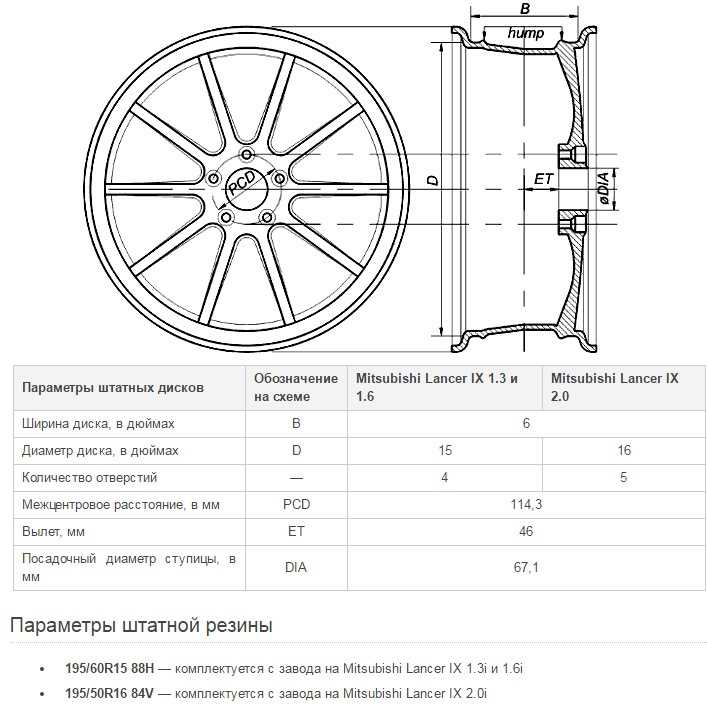 & Бумаги Генрих VIII XIX. я. 148 Запасные колеса для
малый ordynaunce 12 пар, lynce~pynnes, шайбы, [и т. д.].
& Бумаги Генрих VIII XIX. я. 148 Запасные колеса для
малый ordynaunce 12 пар, lynce~pynnes, шайбы, [и т. д.].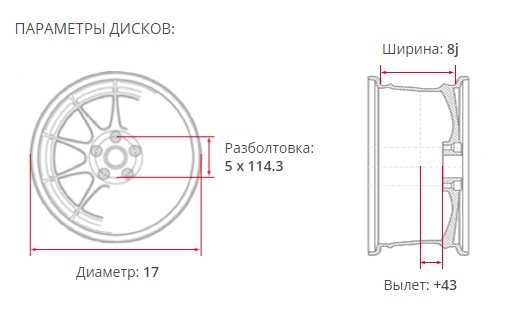
 Хей, Ю. Ф. Чжан, Х. Лю и Л. Ю, «Стабильность и бифуркация нелинейной динамической системы соединения подшипника и гибкого ротора», Труды Институт инженеров-механиков, часть C: Journal of Machine Engineering Science , vol. 223, нет. 4, стр. 835–849, 2009 г.
Хей, Ю. Ф. Чжан, Х. Лю и Л. Ю, «Стабильность и бифуркация нелинейной динамической системы соединения подшипника и гибкого ротора», Труды Институт инженеров-механиков, часть C: Journal of Machine Engineering Science , vol. 223, нет. 4, стр. 835–849, 2009 г. Multi-Body Dynamics , vol. 228, нет. 4, стр. 779–788, 2014.
Multi-Body Dynamics , vol. 228, нет. 4, стр. 779–788, 2014.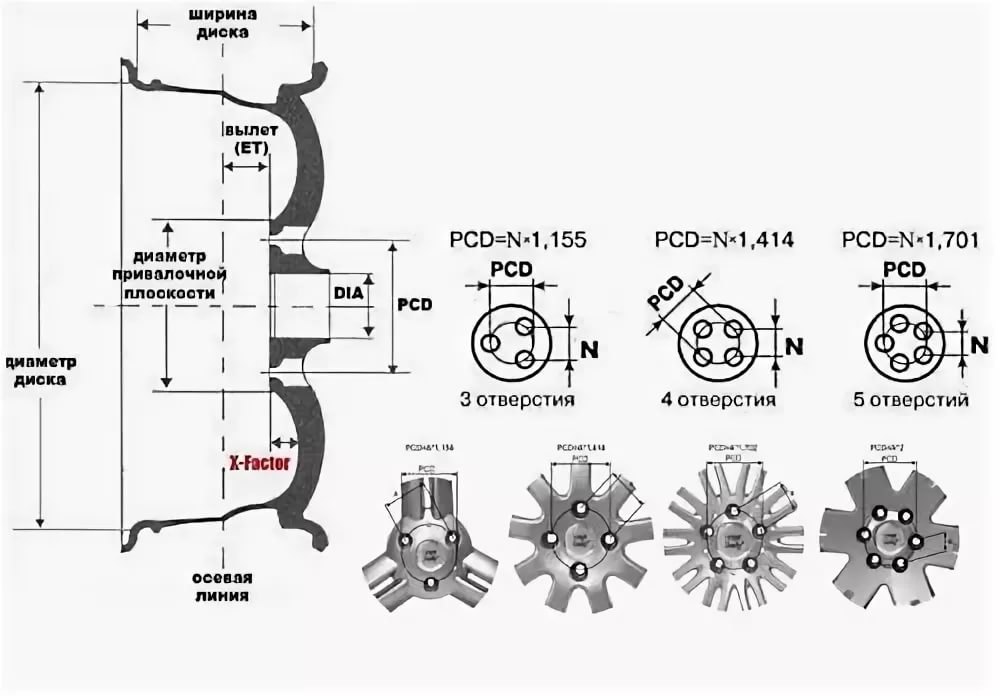 Лю, Х. Лю, Дж. И и М. К. Цзин, «Исследование устойчивости и бифуркации трехмерной системы ротор-подшипник», ASME Journal of Vibration and Acoustics , vol. 135, с. 031017, 2013.
Лю, Х. Лю, Дж. И и М. К. Цзин, «Исследование устойчивости и бифуркации трехмерной системы ротор-подшипник», ASME Journal of Vibration and Acoustics , vol. 135, с. 031017, 2013. Сундарараджан и С. Т. Ноа, «Динамика вынужденных нелинейных систем с использованием метода стрельбы/продолжения длины дуги — применение к роторным системам», Журнал вибрации и акустики , вып. 119, нет. 1, стр. 9–20, 1997.
Сундарараджан и С. Т. Ноа, «Динамика вынужденных нелинейных систем с использованием метода стрельбы/продолжения длины дуги — применение к роторным системам», Журнал вибрации и акустики , вып. 119, нет. 1, стр. 9–20, 1997.