Матричная оптика: Как устроена матричная оптика: — Журнал Движок.

Как устроена матричная оптика: — Журнал Движок.

Борис Игнашин

Постепенный переход на светодиодные источники света в автомобилях уже несомненная тенденция. Лампы накаливания в ближайшем будущем останутся уделом устаревших конструкций. А сейчас высокоэффективные и долговечные фары постепенно отвоевывают позиции у традиционных. В маломощных осветительных приборах светодиоды уже вытеснили конкурентов, а вот в области головного света сражение еще идет. И основное оружие светодиодов — матричная оптика конструкции Hella.

 

Просто заменить газоразрядный или галогенный источник света на светодиоды — идея не новая. Еще в 2008 году подобная система появилась на машинах Lexus LS, а сейчас построенная по тому же принципу головная оптика стала базовой на многих массовых автомобилях. Например, новый кроссовер Skoda Kodiaq оснащен ею в базовой комплектации, как и соплатформенный VW Tiguan. На базе подобной конструкции можно создать даже адаптивное освещение, и оно не будет ничем принципиально отличаться от использующего газоразрядные источники света. Но настоящий прорыв в эффективности дает только матричная светодиодная оптика.

Качественный головной свет автомобиля должен быть не только ярким, но и освещать исключительно необходимые зоны. Кроме того, не слепить встречных водителей, выделять важные объекты и при этом учитывать особенности человеческого глаза в отношении контрастности освещения и светотеневой границы.

Адаптивное головное освещение на базе единого источника света во многом решает эти сложности, но настоящий прорыв возможен только при использовании матричного освещения, когда за каждую зону отвечает отдельный источник света с регулируемой яркостью, а управляется система интеллектуальным модулем, способным распознавать объекты перед машиной и регулировать освещенность различных зон по ситуации. И именно по этому пути пошла компания Hella при разработке своих матричных светодиодных модулей адаптивного освещения.

Идея использовать много фар для освещения нескольких зон перед машиной в случае традиционных источников света сталкивается с габаритными ограничениями. И газоразрядные источники света, и лампы накаливания имеют достаточно крупные размеры рабочей области и требуют объемной оптической системы.

В случае со светодиодным освещением такая проблема не стоит. Если отказаться от использования сменных светодиодных модулей, то на небольшой плате можно разместить более 50 светодиодов, а поскольку их световой поток имеет явную направленность, то подобная матрица диодов отлично работает с компактной и простой оптической системой.

На практике в оптике Audi Matrix LED с 25 светодиодами адаптивного освещения они собраны в сменные модули по пять светодиодов в каждом, и еще пять модулей используются для статического освещения — ближнего света и статического бокового. В следующем поколении оптических систем Hella, которые с 2016 года устанавливаются на машины Mercedes, применяется целых 84 светодиода на единой плате.

Перспективная LED-оптика разработки Hella по-прежнему имеет «всего» 25 светодиодов на единой плате, но за счет использования в оптической системе фары проекционного LCD-дисплея с разрешением 30 тыс. пикселей с матрицей 100х300 число контролируемых зон освещения возрастает на порядок.

Сложность подобной конструкции легко недооценить. При тех же габаритах, что и у традиционной фары, внутри матричная LED-оптика и ее система управления устроены на порядок сложнее. Чтобы не быть голословным, рассмотрим конструкцию и ее возможности на примере оптики Audi Matrix LED для модели A8 в кузове D4 2013 года. Не самой новой, но зато одной из самых распространенных в России и имеющей много общего со светодиодной матричной оптикой других машин Audi. На следующих поколениях и для других моделей, скорее всего, будет уже лазерный источник света.

Помимо конструкции самой оптической системы, важную роль для работы адаптивного освещения играет конструкция системы управления. В случае с матричной оптикой самым важным датчиком системы является LiDAR — дальномер оптического диапазона, позволяющий системе управления получить предоставления обо всех источниках света и объектах в зоне освещения головной оптики. Так же используются данные навигационной системы, датчики скорости автомобиля, дождя и освещенности и данные ассистента ночного видения, если он есть в автомобиле. На основании этих данных блок управления может использовать один из множества режимов работы.

Дальний свет для движения по автомагистрали включается на основании данных навигационной системы. В этом случае система Matrix Beam включает узкий луч с максимальной дальностью освещения, наилучшим образом подходящий для ночных поездок на высокой скорости.

Ближний свет с классической асимметричной формой светового пучка использует 15 отдельных светодиодов в каждой фаре и включается в населенных пунктах. Может применяться отдельно от адаптивного освещения. Дальняя зона освещения реализуется отдельным набором светодиодов и может быть отключена для реализации туристического или всепогодного режима.

Туристический режим используется при движении в странах с левосторонним движением для машин, созданных для движения правостороннего. Он позволяет уменьшить асимметрию светового луча при включенном режиме ближнего света. Включается режим или автоматически, по данным навигационной системы, или вручную, через меню мультимедийной системы.

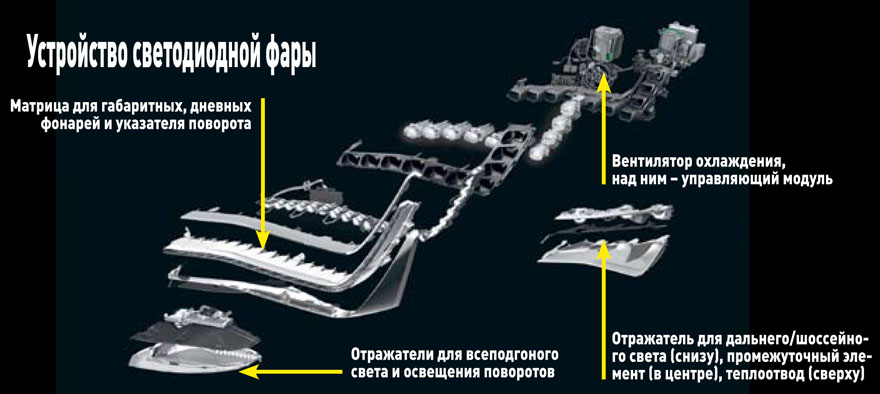
Конструкцию основной оптической системы фары можно увидеть на рисунке, но помимо нее в конструкцию входят также модуль указателя поворота (разумеется, со светодиодами), модуль охлаждения, причем со сменным вентилятором, и внутренняя проводка.

Статическое освещение боковой зоны предназначено для облегчения маневрирования и безопасного проезда перекрестков. Специальная секция фары освещает широкую зону спереди-сбоку от автомобиля. Включается автоматически при малой скорости и включении указателя поворотов, а также при угле поворота рулевого колеса более 50 градусов и скорости менее 60 км/ч. При проезде перекрестков срабатывает режим освещения для перекрестков, который включается по данным навигационной системы и скорости менее 60 км/ч.

Всепогодное освещение используется в условиях тумана и снегопада.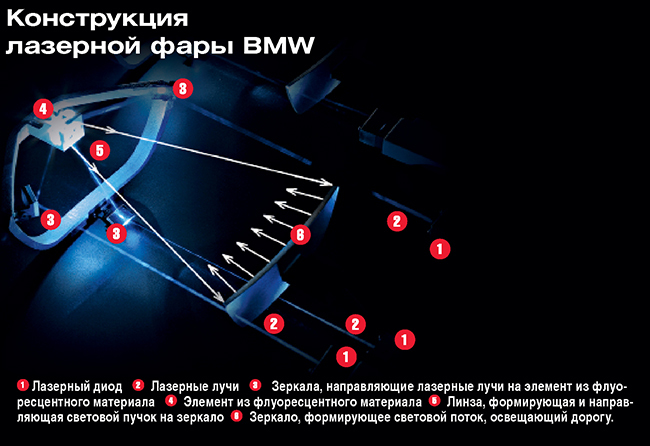 В этом случае снижается мощность ближнего света и включается статическое освещение боковых зон. Включается режим вручную, кнопкой на панели, а ассистент дальнего света при этом отключается.

Динамическое адаптивное освещение работает на скорости более 60 км/ч вне населенных пунктов. Используется матрица из 25 светодиодов дальнего света, создающая 25 независимых сегментов. Система обеспечивает изменение направления луча света в зависимости от рельефа, не ослепляет встречный и попутный транспорт, снижает яркость в зонах расположения источников с высоким коэффициентом отражения — дорожных знаков и все другие функции адаптивности.

Маркирующая подсветка пешеходов срабатывает вне населенных пунктов и скорости более 60 км/ч, при наличии ассистента ночного видения. Секции дальнего света фар в направлении пешехода мигают, привлекая внимание водителя, а силуэт пешехода подсвечивается красным на дисплее приборной панели.

Помимо датчика LiDAR в работе системы задействованы блок управления корректора фар и блок комфорта бортовой сети. Причем самих корректоров у адаптивной оптики нет по двум причинам. На машинах с матричной LED-оптикой установлена пневмоподвеска и сама оптика имеет высокий запас адаптивности даже в режиме ближнего света за счет разделения зон. Так что блок управления в строгом смысле слова блоком коррекции уровня не является, просто располагается и подключен так же, как блок коррекции на машинах без этой системы. Помимо внешних блоков, используются три блока контроля в самой фаре.

Конструкция модуля охлаждения для светодиодной оптики крайне важна, так как от него зависит долговечность самих светодиодов и он включает в себя индивидуальные воздуховоды для каждой диодной сборки и множество датчиков. Вместо линз в этом поколении оптики используются зеркальные отражатели, имеющие повышенную стойкость к перегреву. Снаружи корпус закрыт общим герметичным колпаком.

В целом развитие автомобильного света уже семимильными шагами идет по пути внедрения интеллектуального светодиодного освещения, в чем корреспонденты журнала «Движок» убедились на практике, сравнив его с адаптивным биксеноновым. Ну а постепенное удешевление конструкции и ее повсеместное внедрение в ближайшем будущем позволит значительно улучшить ситуацию с освещением на дороге, а следовательно, и с безопасностью.

Что такое матричные фары и как они работают

В последние годы автомобильная оптика стала гораздо совершеннее. Фары теперь представляют собой не просто лампу с отражателем, а высокотехнологичное устройство, способное выполнять множество функций. Кроме того, всё чаще в них используют яркие светодиоды.

Одна из разновидностей – матричные фары, наиболее совершенный продукт автомобилестроения на сегодняшний день. Впервые они были применены компанией Audi, и её разработки остаются самыми передовыми в этой области.

Благодаря этой технологии вождение в тёмное время суток становится гораздо комфортнее, а безопасность поднимается на новый уровень.

Матричная оптика и ее особенности

Главная особенность матричной фары – использование светодиодов. В ней совсем нет ни ксеноновых, ни галогеновых ламп. На светодиодах работает и дальний, и ближний свет, и указатели поворотов. У разных производителей они могут располагаться по-разному, форма корпуса также бывает разной, но принцип одинаков, и матричные фары невозможно спутать с обычными – у них оригинальный дизайн, и разделение матриц чётко видно.

Особенностью такой конструкции является и её возросшая функциональность. Управляется освещение с помощью освещения, в этом процессе участвует и бортовой компьютер. Используются всевозможные датчики – поворота руля, дождя, освещения, навигационная система, и даже видеокамера.

На основе полученных данных управляющий блок сам принимает решение, как лучше осветить дорогу. Например, при повороте больше света направляется в сторону поворота, а при обнаружении идущего впереди человека он освещается сильнее и становится заметнее. Видеокамера фиксирует встречные автомобили по свету фар и подстраивает освещение таким образом, чтобы оно не било в глаза водителям, но остальные зоны освещаются по-прежнему ярко.

Если используется бортовая навигационная система, то в расчет идут и данные о местности – рельеф, трасса или населенный пункт, и многое другое.

В матричных фарах нет поворотных элементов. В них группы светодиодов заранее расположены оптимальным образом. Уровень света в какой-либо зоне перед автомобилем меняется с помощью изменения яркости определенной светодиодной группы. Это позволяет, например, ярко освещать дорогу, не ослепляя при этом водителя встречного автомобиля.

Как устроена матричная фара

Конструкция самой фары такого типа состоит из отдельных модулей – дальнего света, ближнего света, указателей поворота, габаритов. Всё это оформлено в единый блок, форма которого зависит от конструкции автомобиля и дизайнерских решений.

В каждом модуле используются группы светодиодов. Например, в секции дальнего света их может быть 25 штук, сгруппированных по 5 штук. У каждой группы есть собственный отражатель и радиатор для охлаждения.

Модуль ближнего света тоже состоит из блоков светодиодов, и расположен обычно выше модуля дальнего света. Блок поворотов и габаритов располагают снизу. Спереди фара закрывается прозрачным рассеивателем.

В корпусе фары расположена электроника блока управления и вентилятор с воздуховодом для охлаждения светодиодов.

В новейших моделях Audi используются матрично-лазерные фары. В такой конструкции источником света служит лазер. Его луч, проходя через специальную линзу, покрытую особым флуоресцентным составом, приобретает белый свет, и становится безопасным для глаз. Но мощность такой фары во много раз больше ксеноновой и даже светодиодной. Дальнобойность её может достигать 600 метров против 300 метров для светодиодной и 100 метров для обычной.

Матрично-лазерная фара не только прекрасно освещает дорогу. Она может, как и обычная матричная, избирательно создавать теневые зоны, например, для встречных автомобилей. Кроме того, она может регулировать створ луча. Например, при движении по трассе на большой скорости луч становится уже, свет сконцентрирован в более узком пучке, светит дальше и ярче. При медленном движении, например, по населенному пункту, луч расширяется, захватывая больше окружающей местности.

Разновидность функций освещения в матричной оптике

Сложное устройство фар позволяет им выполнять множество функций. Матричные фары, как светодиодные, так и лазерные, обеспечивают:

• Дальний свет, который можно не переключать, если навстречу двигаются другие автомобили. Для них создаются теневые зоны, и водители не ослепляются. Такая зона создается и для автомобиля, расположенного впереди. При этом остальное пространство освещается с прежней яркостью, и видимость не уменьшается.
• Ближний свет обычного вида, когда боковые сектора и обочина освещаются сильнее, а луч света опускается вниз.
• Адаптивное освещение, которое подстраивается в зависимости от манёвра. Например, при повороте задействуются дополнительные боковые светодиоды, улучшающие видимость сбоку. Кроме того, луч света в последних моделях может поворачиваться при плавных изгибах дороги, подсвечивая опасные места.
• Всепогодное освещение, которое меняет свою интенсивность на основе данных от различных датчиков. Движение в дождь, туман, пургу, становится гораздо безопаснее и комфортнее.
• Подсвечивание пешеходов и знаков основано на данных с видеокамеры. Фары сигнализируют трехкратным изменением яркости, предупреждая людей и животных, оказавшихся на опасном расстоянии от автомобиля.
• Динамический указатель поворотов гораздо лучше показывает направление манёвра, чем обычный. «Бегущие огни» из 30 светодиодов заметны издалека, привлекают внимание и информативнее.

Как видите, матричные фары гораздо удобнее в пользовании, чем обычные. Они избавляют водителя от ручного переключения дальнего и ближнего света, обеспечивают лучшую видимость в любых условиях, а для окружающих не создают неудобств.

Преимущества и недостатки матричной оптики

Большим плюсом нового типа фар является удобство, интеллектуальное управление, повышенная безопасность в темное время суток или при плохих погодных условиях. Расположенные матрицами светодиоды обеспечивают более яркий свет в нужном направлении. Всё это, конечно, нравится водителям.

Но у матричных фар есть один большой недостаток – стоимость. Они могут стоить тысячи и десятки тысяч долларов за штуку. Стоит только нечаянно стукнуть и придётся покупать очень дорогостоящую деталь, притом её придётся заказывать у производителя. Кроме того, при выходе из строя даже одного светодиода придётся менять всю фару. Хотя производитель и даёт гарантию в 10 лет, но это может случиться.

 

Несмотря на это, функционал матричных фар настолько превосходит обычные, что всё больше автопроизводителей внедряют эту технологию на своих автомобилях. Со временем, возможно, и цена на них заметно снизится.

Оптика. Матричная теория Гауссовой оптики.

(Лекция 6)

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Оптика.

Лекция 6.
Матричная теория Гауссовой оптики

2. Преобразование координат лучей оптической системой

Основное действие оптической системы заключается в изменении хода лучей, которое
описывается преобразованиями двух параметров – линейной и угловой координат
луча. Эти преобразования наиболее удобно описывать при помощи
аппарата матричной оптики. Матрица преобразованияполностью описывает
распространение лучей через оптическую систему.
Параметры луча в пространстве
предметов и изображений могут быть
заданы только в том случае, если
выбраны опорные плоскости. Опорная
плоскость (ОП) – это некоторая
произвольно выбранная плоскость,
перпендикулярная оптической оси.
Опорные плоскости в пространстве
предметов и изображений выбираются
из соображений удобства и могут быть
либо сопряженными, либо нет.
Вместо угла α часто используют направляющий косинус оптического лучевого вектора:
Y n cos y n sin n
y
Y
(ОС)
y
Y
y a0 a1 y a2Y a3 y 2 a4 yY a5Y 2 …
Y b0 b1 y b2Y b3 y 2 b4 yY b5Y 2 …
Если оптическая система является центрированной, то a0=b0=0. Все члены ряда,
начиная с a3 и b3, можно отбросить, так как они стремятся к нулю на порядок
быстрее, чем предыдущие. Таким образом, для идеальной оптической системы:
y Ay BY
Y Cy DY

4. Матрица преобразования лучей

y A B y
Y C D Y
Все свойства идеальной оптической системы полностью описываются матрицей
преобразования лучей , называемой также гауссовой матрицей или ABCD-матрицей
A B
G
C D

5.

Геометрический смысл элементов матрицы преобразованияРассмотрим луч с координатами , y=1, Y=0
y Ay BY A
Y Cy DY C
y
f
y
S F
C учетом того, что , y=1 можно получить
S
y S F F
f
Y n
S F
f
n
C
f
A
n
f

6. Геометрический смысл элементов матрицы преобразования

Рассмотрим луч с координатами , Y=1 (α=-1/n), Y’=0 (α’=0)
y Ay BY Ay B
Y Cy DY Cy D 0
f
y f
n
S
y S F F
n
C учетом того, что , y=1 можно получить
S
y S F F
f
n
f
n S F n S F S F
D Cy
f
n
f
n
f
f S S S S
f S S f f
B y Ay F F F F F F
n f n
n f
n
n f
Y n

7. Геометрический смысл элементов матрицы преобразования

S F
f
G
n
f
S F S F f f
n f
SF
f
Элемент матрицы С зависит только от
параметров оптической системы, а
элементы A,B, D и зависят еще и от
выбора опорных плоскостей.
Определитель матрицы преобразования
det G AD BC 1

8. Обратная матрица преобразования

G -1G GG 1 I
1 0 — единичная матрица
I
0
1
Обратная матрица преобразования описывает обратное преобразование (из выходных
координат во входные)
b G 1 b
D B
1
G
C
A
Условие сопряжения опорных плоскостей
В общем случае все элементы матрицы преобразования не равны нулю, но для
случая сопряженных опорных плоскостей элемент B=0. Для сопряженных опорных
плоскостей элемент A имеет значение линейного увеличения, а элемент D — величина
обратная элементу A.

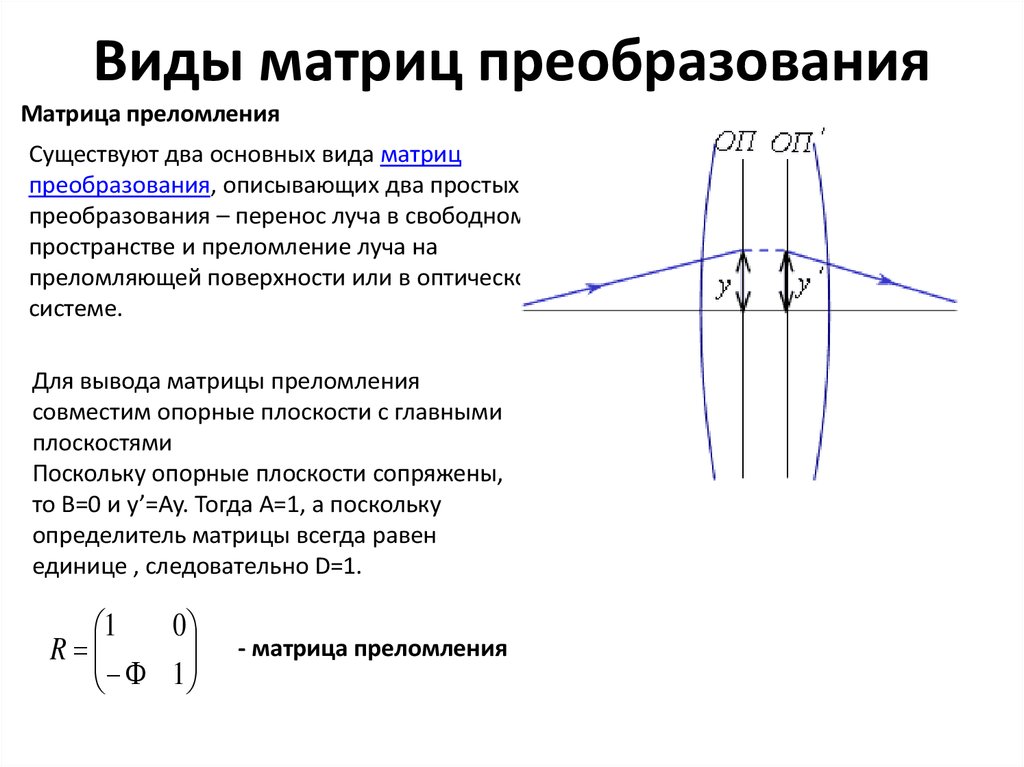
9. Виды матриц преобразования

Матрица преломления
Существуют два основных вида матриц
преобразования, описывающих два простых
преобразования – перенос луча в свободном
пространстве и преломление луча на
преломляющей поверхности или в оптической
системе.
Для вывода матрицы преломления
совместим опорные плоскости с главными
плоскостями
Поскольку опорные плоскости сопряжены,
то B=0 и y’=Ay. Тогда A=1, а поскольку
определитель матрицы всегда равен
единице , следовательно D=1.
0
1
R
1
— матрица преломления

10. Виды матриц преобразования

Матрица переноса
При переносе луча изменяется только линейная
координата.
Y
y y d y d
n
Угловая координата не изменяется
Y Y
d
1
T
n — матрица переноса
0
1
d
— приведенное расстояние между опорными плоскостями
n

11. Матрица одной преломляющей поверхности

Из
треугольников OKC и CKO’
можно вывести
Домножим оба выражения
на n и n’ соответственно
n n n
n n n
Из закона преломления следует, что
n n
n n n n
y
Y Y n n
r
y
r
Y Y y n n
0
1
R
n n 1

12. Матрица зеркальной (отражающей) поверхности

n n
0
1
R
2 n 1
Для плоского зеркала
1 0
R
0 1
Следовательно, плоское зеркало не меняет хода луча (геометрический косинус
изменяется, а оптический преломленный (отраженный) косинус остается прежним).

13. Матрицы оптической системы, состоящей из нескольких компонентов

Любую оптическую систему можно представить как совокупность нескольких
компонентов, разделенных промежутками. Пусть дана некоторая произвольная
система, в которой для каждого компонента известно положение главных
плоскостей и оптическая сила, а также известны расстояния между компонентами
и показатели преломления
G T3 R3T2 R2T1T0 Tn Rn …T1R1T0
1
Rn
1
0
, Tn
1
dn
nn
1

14. Пакет из плоскопараллельных слоев

d 2 d1 d1 d 2
1
1
1
G T2T1 n2 n1 n1 n2
0 1 0 1 0
1
dn
d1 d 2
1 t
t t1 t2 … tn …
T
n1 n2
nn
0 1

15. Оптическая система с нулевыми расстояниями между компонентами

0 1
0 1
1
G R2 R1
2 1 1 1 1 2
0
1
то есть оптические силы таких компонент складываются
1 2 … n

16. Двухкомпонентная оптическая система

G R2 DR1
1 2 1 2
d
n
Рассмотрим частные случаи двухкомпонентной системы.
Если d=0, тогда Ф=Ф1+Ф2.
Если t=d/n=1/Ф1, это значит, что второй компонент (его главная плоскость) находится
в заднем фокусе первого компонента. Тогда Ф=Ф1, то есть второй компонент может
иметь какую угодно оптическую силу.
Если t=d/n=1/Ф1, то первый компонент находится в переднем фокусе второго
компонента, тогда Ф=Ф2.
d 1 2 1 1
Если t
n 1 2 1 2
то
0

17. Афокальные (телескопические) системы

Афокальные или телескопические системы – это системы из двух или более
компонентов, оптическая сила которых равна нулю. Такие системы предназначены для
наблюдения удаленных объектов.
У афокальных систем оптическая сила равна нулю, то есть C=-Ф=0, следовательно,
определитель матрицы detG=AD-BC. Отсюда D=A-1. Тогда матрица будет выглядеть
следующим образом:
A B
G
1
0 A
Если опорные плоскости сопряжены, то B=0 , и следовательно:
A 0
G
1
0 A
y Ay BY Ay
Y Cy DY A 1Y
Для афокальной системы элемент матрицы равен линейному (поперечному)
увеличению, а его обратная величина имеет смысл углового увеличения:
В телескопических системах линейное и угловое увеличение не зависят от положения
сопряженных опорных плоскостей и, следовательно, не зависят от положения
предмета и изображения:
y
const A
y
Y
const A 1
Y
t
Двухкомпонентная оптическая система телескопическая,
если задний фокус первого компонента совпадает
с передним фокусом второго
d 1 2 1 1
n 1 2 1 2
Линейное увеличение такой системы:
y f 2
y f1

19.

Матрица тонкой линзы1
G R2T1 R1
2 n 1
0 1
1
0
1
G R2T1R1
1 2 n 1
d
1
n
n 1
1 1
0
1
0
1

20. Расчет параксиальных (нулевых) лучей через оптическую систему

Нулевые лучи – это лучи, которые преломляются по законам параксиальной оптики, но
имеют произвольно большие координаты.
Расчет нулевых лучей через оптическую систему состоит из операций переноса луча
между компонентами и преломления луча на компонентах, которые можно описывать
либо в матричной форме, либо в виде рекуррентных соотношений:
d
y y Y
n
Y Y y
Вычисления выполняются столько раз, сколько компонентов имеется в оптической
системе. Однако, для полного расчета лучей через оптическую систему вначале
нужно определить координаты лучей в пространстве предметов, а после завершения
расчетов определить координаты лучей в пространстве изображений. Таким
образом, расчет нулевых (параксиальных) лучей включает в себя три этапа:
определение входных координат луча,
вычисление хода луча (последовательное определение его координат на всех
компонентах),
определение выходных координат луча.

English     Русский Правила

Устройство и особенности работы матричных фар

Nevada 1976Устройство и особенности работы матричных фар 0 Comment

Содержание статьи

Эволюция автомобильного освещения совершила грандиозный рывок с появлением матричных фар. На сегодняшний день – это самый прогрессивный и высокотехнологичный вариант автомобильной оптики. В чем преимущества матричных светодиодных фар и каков принцип их работы?

В области технологий освещения, ведущие позиции принадлежат Audi. Последней разработкой компании являются матричные фары, благодаря которым комфорт управления и уровень безопасности движения поднимается на качественно новый уровень.

Начиная с 2013 года матричные фары (Matrix LED headights) устанавливаются на флагман Audi – модель А8. Компания Opel разрабатывает Matrix Beam (пилотный проект матричных фар).

Матричные фары от Audi объединяют в себе блок управления, воздуховод с вентилятором, дизайнерское обрамление, модуль габаритных огней, дневных огней и указателя поворота, и, конечно же, модуль ближнего света фар и модуль дальнего света фар.

Матричная оптика и ее особенности

Главная особенность матричной фары – использование светодиодов. В ней совсем нет ни ксеноновых, ни галогеновых ламп. На светодиодах работает и дальний, и ближний свет, и указатели поворотов. У разных производителей они могут располагаться по-разному, форма корпуса также бывает разной, но принцип одинаков, и матричные фары невозможно спутать с обычными – у них оригинальный дизайн, и разделение матриц чётко видно. Особенностью такой конструкции является и её возросшая функциональность.

Управляется освещение с помощью освещения, в этом процессе участвует и бортовой компьютер. Используются всевозможные датчики – поворота руля, дождя, освещения, навигационная система, и даже видеокамера. На основе полученных данных управляющий блок сам принимает решение, как лучше осветить дорогу. Например, при повороте больше света направляется в сторону поворота, а при обнаружении идущего впереди человека он освещается сильнее и становится заметнее.

Видеокамера фиксирует встречные автомобили по свету фар и подстраивает освещение таким образом, чтобы оно не било в глаза водителям, но остальные зоны освещаются по-прежнему ярко. Если используется бортовая навигационная система, то в расчет идут и данные о местности – рельеф, трасса или населенный пункт, и многое другое. В матричных фарах нет поворотных элементов. В них группы светодиодов заранее расположены оптимальным образом. Уровень света в какой-либо зоне перед автомобилем меняется с помощью изменения яркости определенной светодиодной группы. Это позволяет, например, ярко освещать дорогу, не ослепляя при этом водителя встречного автомобиля.

Принцип работы матричных фар

Модуль дальнего света фар состоит из двадцати пяти светодиодов, которые объединены в группы по пять штук, образующих матрицу. Каждая группа обладает своим металлическим радиатором для охлаждения и своим отражателем. Благодаря матрице, из светодиодов реализуется порядка миллиарда разных комбинаций распределения света.

Что касается модуля ближнего света фар, то он расположен над модулем дальнего света. Он тоже состоит из светодиодов, которые разделены на несколько групп. В самой нижней части фары расположен модуль указателя поворота, габаритных огней и дневных ходовых огней. Включает модуль тридцать последовательных светодиодов.

Дизайнерское обрамление подчеркивает расположение модулей освещения. Кроме этого в матричной фаре размещен электронный блок управления. В целях принудительного охлаждения светодиодов, фары вооружены воздуховодом с вентилятором.

Все конструктивные элементы таких фар находятся в пластмассовом корпусе, который является основой для размещения элементов и защитой от внешнего воздействия. Прозрачный рассеиватель закрывает корпус с лицевой части.

Матричные фары оснащены электронной системой управления, которая традиционно включает в себя блок управления, входные устройства и исполнительные элементы. Под входными устройствами подразумеваются GPS навигационная система, видеокамера и ряд датчиков. Навигационная система предоставляет водителю сведения о рельефе дороги (подъемы, спуски, повороты), а видеокамера дает информацию о прочих автомобилях, находящихся на дороге.

В «интересах» фар работает большое количество датчиков прочих систем автомобиля, таких как датчик угла поворота рулевого колеса, датчик дорожного просвета, датчик скорости движения, датчик дождя и датчик освещения. Информация, поступающая от входных устройств, обрабатывается электронным блоком управления, который в зависимости от ситуации на дороге активирует определенные светодиоды или дезактивирует их.

Поворотные механизмы в матричных фарах не используются подобно тому как они используются в ксеноновых фарах. Все рабочие функции матричных фар выполняются только с помощью статических светодиодов и электроники.

Из каких элементов состоит матричное освещение автомобиля?

Основные элементы матричных фар – это модули дальнего и ближнего света , с конструкционными особенностями которых мы хотим вас познакомить более подробно.

1. Модуль дальнего света представляет собой набор из 25 светодиодов. Все светодиоды разделены на 5 групп по 5. При этом каждая группа образует специальную матрицу, которая оснащается отдельным отражателем и радиатором, способствующим их охлаждению. Благодаря такому расположению матрицы могут воспроизводить любую мощность и интенсивность света, по необходимости меняя даже его направленность. При необходимости модель дальнего света можно вмонтировать в обычный автомобиль по стандартной схеме.

2. Модуль ближнего света состоит из 30 светодиодов, которые также разделены на несколько сегментов. Для максимально быстрого и эффективного охлаждения модуль оснащен воздуховодом и вентилятором. Размещается модуль внизу основной фары, вместе с модулем дневных ходовых огней, габаритных огней и динамических поворотников.

Таким образом, матричные фары состоят из большого количества модулей, которые очень грамотно объединены в одной фаре и, благодаря специальному программному обеспечению, способны функционировать практически без вмешательства человека.

Интересно знать! Противотуманные фары могут иметь либо белый, либо специальный желтый цвет. Однако на обеих фарах должны стоять лампы одинакового света.

Разновидность функций освещения в матричной оптике

Чем сложней устроена конструкция оптики, тем больше функций она может выполнять. В матричной оптики насчитывают девять разновидностей функций освещения:

• постоянный дальний свет;
• освещение для автомагистралей;
• ближнее освещение;
• адаптивное освещение;
• освещение на перекрестках;
• освещение в любую погоду;
• подсвечивание пешеходов;
• адаптивное динамическое освещение;
• динамический указатель поворотов.

Список не малый как видим, рассмотрим по каждому пункту отдельно, как устроен и принцип освещения.

Полисегментальный дальний свет позволит водителю двигаться с постоянным включенным дальним светом. В таком случае будут задействованы 25 отдельных светодиодов дальнего света. Так же будет задействована видеокамера, которая в темное время суток следит за встречными и попутными автомобилями по их свету фар. Как только обнаружен автомобиль, блок управления выключает часть светодиодов, которые направлены на движущийся автомобиль. Свободное пространство дороги будет освещаться в прежнем виде. Для уменьшения ослепления водителей яркость оставшегося блока матричной оптики будет уменьшена. По данным с паспорта, блок управления матричных фар одновременно может распознать до восьми автомобилей.

Свет для движения по автомагистрали основывается на полученную информацию с навигационной системы. Адаптивная система сужает конус дальнего света матричных фар, таким образом, чтоб максимально направить вперед и сделать удобной для других водителей.

Ближнее освещение имеет традиционную форму, средняя часть дороги освещается меньше, а вот боковая часть и обочина больше. При этом матричная оптика направляется вниз в зависимости от рельефа дороги и населенного пункта.

Адаптивный свет направлен на лучшее освещение машины спереди и сбоку во время выполнения маневра поворота. В таком случае система матричных фар в каждой из фар задействует по три светодиода, которые включаются или выключаются при повороте руля или срабатывании поворотов.

Освещение перекрестков 

предназначено для освещения перекрестков при приближении к ним. В этом случае для матричных фар так же задействована навигационная система, на основе информации которой и определяется перекресток.

Всепогодное освещение из самого названия говорит о том, что при движении в плохих погодных условиях (туман, дождь, снег) будет меняется качество освещения. Блок управления настроить светодиоды матричной оптики таким образом, чтоб избежать ослепления от своих же фар. Интенсивность светодиодов матричной фары будет меняться в зависимости от видимости.

Подсвечивание пешеходов в матричных фарах реализовано на высоком уровне. В случае обнаружения пешехода с помощью камеры и системы ночного виденья, на обочине или опасной близости от нее оптика будет троекратно сигнализировать дальним светом об этом. Тем самым предупреждать как водителя, так и пешехода.

Динамическое адаптивное освещение 

это предпоследний вариант в матричных фарах. Суть его работы направлена на освещение дороги во время поворота. Поворачивая рулевое колесо, яркость светового пучка перенаправляется с центральной части в сторону поворота. То есть одна часть светодиодов становится тусклее, другая ярче.

Динамический указатель поворотов матричных фар рассчитан на управляемое движение светодиодов в направлении поворота. Таким образом, 30 последовательных светодиодов оптики включаются последовательно с периодичностью в 150 мс. Со стороны это не только красиво выглядит, но и дает больше информации о том или этом маневре автомобиля.

Многие производители уже готовят свои автомобили под внедрение подобной технологии матричной оптики, но насколько это удастся, пока никто не может сказать. На данный момент компания Audi является единственным правообладателем подобной технологии в оптике и захочет ли она делиться с другими производителями остается под вопросом

На уровне с иными производителями автомобилей и автомобильной светотехники, компания Audi занимает лидирующие позиции. Данный производитель за последнее время сумел разительно отличиться от иных. Показательной стала работа над современной разработкой – матричными фарами. Фары стали не только уникальным достижением, но и настоящей изюминкой автомобилей известного завода.

Подобное достижение имеет не столько эстетические совершенства, сколько технические. Так уровень безопасности при передвижениях по автострадам вышел на новый уровень.

Матричные фары также придают процессу вождения и дополнительный комфорт, что также имеет большое значение. Теперь водители могут не просто управлять любимым автомобилем, но и получать недюжинное удовлетворение от самого процесса.

Какие производители применяют подобные фары

Автопроизводители стараются активно внедрять новые решения в свою технику. И если говорить о матричных фарах, то на текущий момент их использует ряд компаний: Matrix Beam от Opel, которая корректирует работу оптики исходя из погодных условий, скорости и маршрута движения, загруженности транспорта.

Matrix LED от Audi устанавливается только в новые автомобили марки A8. Технология доступна исключительно для дорогих машин. Светодиодные матричные фары от Volkswagen IQ Light — каждое устройство состоит из 128 светодиодов. Работоспособность освещения гарантирует интеллектуальная система, приспособленная к любым режимам движения.

Преимущества матричных фар

Матричные фары реализуют ряд прогрессивных функций:

• Обнаружение пешеходов и их подсвечивание;
• Распознавание автомобилей, а также изменение светового луча;
• Динамические указатели поворотов;
• Адаптивное освещение поворотов.

Во время движения автомобиля по дороге в темноте, видеокамера обнаруживает попутные и встречные автомобили по их освещению. Сразу же по обнаружении автомобиля, системой управления включаются светодиоды, которые направляют на обнаруженную машину свет. Все оставшееся пространство дороги полностью освещается. При этом стоит отметить, что чем ближе обнаруженный автомобиль, тем сильнее включаются светодиоды. Однако при этом ослепление водителя едущего навстречу транспортного средства полностью исключено. Одновременно матричные фары способны выявлять до восьми машин.

Кроме автомобилей матричные фары могут обнаруживать в темноте животных и пешеходов, причем как тех, что находятся на дороге, так и тех, которые находятся поблизости от нее. Именно с этой целью матричные фары соединены с системой ночного видения.

Обнаружив пешехода или животное, фары подают дальним светом трехкратный сигнал, предупреждая и самого водителя, и пешехода.

С помощью навигационной системы реализуется адаптивное освещение поворотов. На основе данных навигационной системы, поворот освещается еще до того, как водитель начнет поворачивать руль. Благодаря адаптивному освещению, обеспечивается лучшая видимость и, соответственно, повышается безопасность движения на дороге.

Динамический указатель поворотов является управляемым (в направлении поворота) движением огней. Чтобы реализовать эту функцию, тридцать светодиодов последовательно включаются с периодичностью в сто пятьдесят миллисекунд. И, согласно заявлениям производителя, благодаря динамическому указателю поворотов информативность системы освещения транспортного средства существенно повышается.

Устройство,виды и принцип работы системы пассивной безопасности SRS

Система непосредственного впрыска топлива GDI: что это такое и как работает?

Насос системы охлаждения двигателя (помпы): устройство виды и принцип работы,фото

Топливный насос высокого давления (ТНВД): что это такое и для чего он нужен,виды,фото

Что такое матричные фары и чем рни отличаются от других

Что такое матричные фары

Матричные фары — нашумевшая во всем мире технология на основе светодиодов, разработанная и популяризированная компанией Audi. Полное название системы «Audi Matrix LED». Устройство реализует основные функции головного освещения автомобиля, включая дальний и ближний свет.

Внешний вид матричной фары Audi Matrix LED

В отличие от стандартной оптики, матричные фары представляют собой сложную систему из светодиодов, контроллеров и интеллектуальных модулей. В случае с обычными фарами, водитель только включает определенный режим, а освещение работает согласно установленным параметрам. Матричная же оптика делится на функциональные сегменты и в автоматическом режиме регулирует яркость и освещенность определенных зон в зависимости от дорожной ситуации.

Водителю больше не нужно думать про переключение режимов света, поскольку управлением занимается встроенная интеллектуальная система.

Дальний свет

25 светодиодов образуют своеобразную матрицу, которая делится на 5 блоков. В каждом блоке размещены по 5 светодиодов.

Каждый светодиодный блок имеет свою систему охлаждения, в которую входит металлический радиатор, и отражатель (рефлектор с линзой).

Благодаря такой технологии стало возможным распределять свет одним миллионом комбинаций, что не возможно было сделать на других видах фар.

Сейчас
читают
Что будет если перелить масло в двигатель

Как правильно проверить уровень масла в двигателе

14.5k

Преимущества перед остальными типами фар

Как мы уже упоминали, светодиодные источники света стали постепенно вытеснять традиционные. Причиной послужила их экономичность и более длительный срок эксплуатации. И если говорить про матричные фары, то они обладают целым рядом дополнительных преимуществ:

1. Габаритные размеры — галогенная и газоразрядная оптика требуют большого пространства для установки, а светодиоды легко разместить даже на маленькой плате.
2. Срок эксплуатации — система состоит из минимального набора элементов, которые подвержены сбоям и выходу из строя.
3. Яркость освещения — показатель регулируется количеством установленных светодиодов.
4. Управление освещенностью зон — с помощью датчиков и систем распознавания автомобиля происходит автоматический анализ объектов и изменение световых режимов.

Работа системы в темное время суток

В зависимости от режима работы матричные фары могут обеспечить яркий и тусклый свет, а также изменять фокус.

Распознавание автомобилей

Основное предназначение данной функции, это предотвращение ослепления водителей, которые движутся как в попутном, так и во встречном направлениях.

Как Вы уже догадались она работает в темное время суток и выявление автомобиля происходит с помощью специальной видеокамеры по его источникам света.

Однако на некоторых автомобилях впереди может стоять специальный радар, который также фиксирует расположение других машин на дороге.

При обнаружении транспортного средства система автоматически отключает те светодиоды, потоки света от которых максимально направлены на машину.

Чем ближе к Вам машина, тем больше направленных на нее светодиодов отключается, но при этом освещенность окружающего пространства остаётся неизменным.

Работа системы рассчитана на определение до 8 автомобилей, что вполне достаточно.

Основные функции матричных фар

Матричные фары регулируются с помощью электронного блока управления, который обеспечивают работу следующих функций освещения:

• сегментальный дальний свет;
• ближний свет с асимметричной формой;
• статичное адаптивное освещение;
• дальний свет для автомагистрали;
• освещение перекрестков;
• динамическое освещение поворотов;
• всепогодный свет;
• динамический указатель поворотов.

Распознавание пешехода системой Volkswagen IQ Light

Система может подсвечивать пешеходов и животных, находящихся на дороге или в непосредственной близости на обочине.

До полукилометра

Расставив на прямом участке трека щиты через каждые 100 м, делаем несколько заездов. От наших испытателей, собственно, ничего особенного не требуется: две дополнительные фары включаются по команде электроники, управляющей дальним светом. Вводные же электроника получает от установленной на ветровом стекле телекамеры, которая следит за дорогой.

На практике оказалось, что лазерные фары включаются только на скоростях выше 60 км/ч, только на неосвещенных участках и только при условии, что впереди нет попутных и встречных автомобилей. Как только камера замечает на обочине включенный фонарь, электронная система автоматически переходит на ближний свет: фары светодиодные, и их вполне хватает. Когда же система, наконец, решает, что пора, сначала включаются обычные фары дальнего света (они сами по себе гарантируют видимость на расстоянии до 300 м), а через мгновение дорогу заливает дальнобойный свет лазерных прожекторов.

Результат поразительный. Мы не можем безоговорочно подтвердить, что дорога, как это заявляет производитель, освещается на 600 м, но что луч света уходит за полкилометра — факт. Ну и, конечно, ощущения: когда работают лазерные фары, контроль над дорогой полный. Исключительно из любопытства (на дороге это делать категорически не следует) мы решили проверить, насколько быстрее позволяют ехать лазерные фары. В качестве точки отсчета взяли собственные ощущения при движении на скорости 130 км/ч со светодиодными фарами.

Потом включили лазерные. Прикинули, посчитали и пришли к выводу, что новое изобретение позволяет контролировать дорогу ничуть не хуже на скоростях до 260 км/ч и даже больше.

Не говоря об ограничениях, которые накладывает закон, и о здравом смысле, мы считаем, что есть вполне убедительная причина не повторять подобные экзерсисы на дорогах общего пользования: если телекамера вдруг обнаружит, что навстречу едет другой автомобиль, система моментально выключит лазеры. Оказаться на темной дороге на такой скорости с одними светодиодами — участь незавидная.

Полезное: Что это такое пневмоподвеска?

Из каких элементов состоит матричная фара

Поскольку в основе матричной фары лежат светодиоды, они являются неотъемлемой частью конструкции. Использование данного вида источников света позволяет улучшить качество и яркость освещения. В список конструктивных элементов фары входят:

• светодиодные матрицы ближнего и дальнего света;
• модули ДХО, указателей поворота и габаритов;
• пластмассовый корпус с прозрачным рассеивателем;
• вентилятор охлаждения;
• декоративная решетка;
• блок управления.

Конструктивные особенности матричной оптики
Поскольку система управляется автоматически, блок управления обменивается сигналами с другими модулями автомобиля, а также датчиками движения и видеокамерой.

Переключение угла освещения, яркости и режима работы фар происходит на основе информации с датчиков и навигационных систем транспортного средства.

Матричная оптика и ее особенности

Главная особенность матричной фары – использование светодиодов.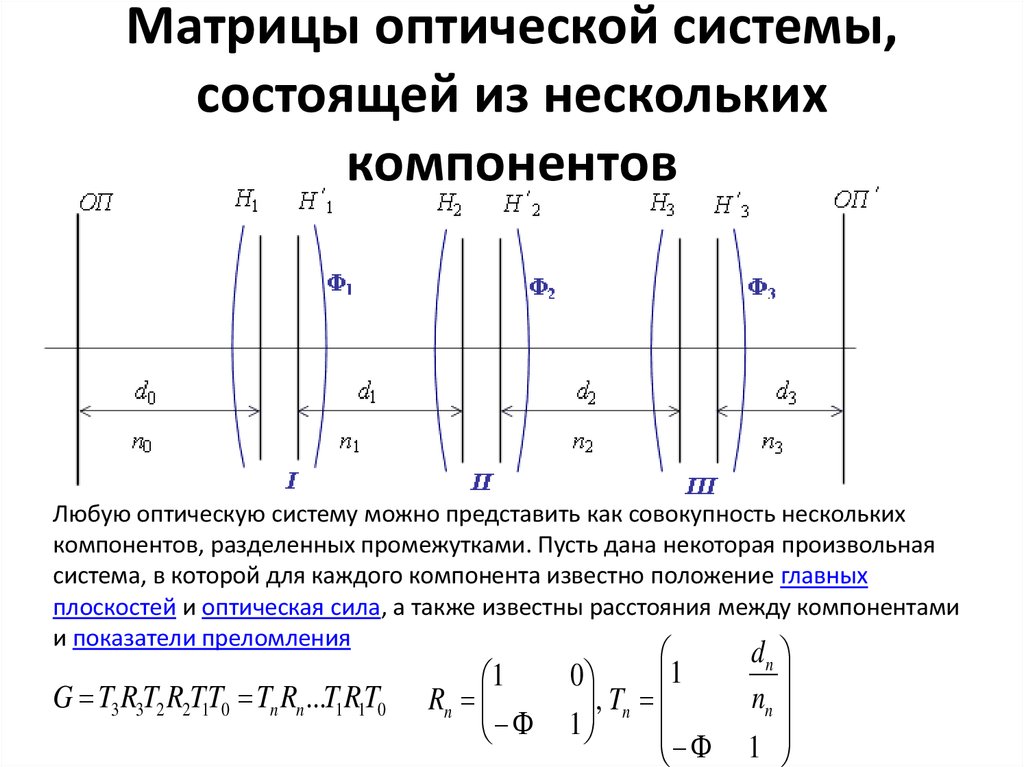 В ней совсем нет ни ксеноновых, ни галогеновых ламп. На светодиодах работает и дальний, и ближний свет, и указатели поворотов. У разных производителей они могут располагаться по-разному, форма корпуса также бывает разной, но принцип одинаков, и матричные фары невозможно спутать с обычными – у них оригинальный дизайн, и разделение матриц чётко видно.

Особенностью такой конструкции является и её возросшая функциональность. Управляется освещение с помощью освещения, в этом процессе участвует и бортовой компьютер. Используются всевозможные датчики – поворота руля, дождя, освещения, навигационная система, и даже видеокамера.

На основе полученных данных управляющий блок сам принимает решение, как лучше осветить дорогу. Например, при повороте больше света направляется в сторону поворота, а при обнаружении идущего впереди человека он освещается сильнее и становится заметнее. Видеокамера фиксирует встречные автомобили по свету фар и подстраивает освещение таким образом, чтобы оно не било в глаза водителям, но остальные зоны освещаются по-прежнему ярко.

Если используется бортовая навигационная система, то в расчет идут и данные о местности – рельеф, трасса или населенный пункт, и многое другое.

В матричных фарах нет поворотных элементов. В них группы светодиодов заранее расположены оптимальным образом. Уровень света в какой-либо зоне перед автомобилем меняется с помощью изменения яркости определенной светодиодной группы. Это позволяет, например, ярко освещать дорогу, не ослепляя при этом водителя встречного автомобиля.

Логика и принцип работы системы освещения

Рассмотрим пример работы матричной оптики в рамках разработки Audi Matrix LED. Каждая фара автомобиля состоит из 5 секций, которые оснащены пятью светодиодами. В общей сумме получается 25 элементов на одного устройство. При этом для каждой группы светодиодов предусмотрена собственная линза, позволяющая изменять фокус, яркость и направленность освещения.

Блок управления контролирует и управляет работой матричных фар. Специально для отслеживания дорожной ситуации в передней части автомобиля расположен датчик, позволяющий обнаруживать приближение встречного автомобиля. При поступлении сигнала от сенсора система изменяет количество рабочих секций, чтобы не ослеплять водителей, но поддерживать достаточный уровень освещенности.

Системы света с матричной оптикой синхронизированы с устройствами навигации, а также получают данные о внешней среде от видеокамеры. Это позволяет увеличить количество режимов работы, а также распознавать объекты и фокусироваться на них.

Сравнение стандартной и матричной системы

Какие производители применяют подобные фары

Автопроизводители стараются активно внедрять новые решения в свою технику. И если говорить о матричных фарах, то на текущий момент их использует ряд компаний:

1. Matrix Beam от Opel, которая корректирует работу оптики исходя из погодных условий, скорости и маршрута движения, загруженности транспорта.
2. Matrix LED от Audi устанавливается только в новые автомобили марки A8. Технология доступна исключительно для дорогих машин.
3. Светодиодные матричные фары от Volkswagen IQ Light — каждое устройство состоит из 128 светодиодов. Работоспособность освещения гарантирует интеллектуальная система, приспособленная к любым режимам движения.

Технология матричной оптики Opel Matrix Beam

⇡#Электрокары и гибриды

Хотя работающие на водороде автомобили не являются ни электрокарами, ни гибридами, мы все же отнесем их именно к этой категории. По большому счету водородомобили близки к чистым электромобилям с той лишь разницей, что они могут сами вырабатывать электричество. Наиболее актуальной новинкой в этой сфере является седан Toyota Mirai, по основным потребительским качествам приближенный к рядовым машинам с ДВС. На полностью заправленном баллоне водорода он проезжает около 500 километров, а разгон с 0 до 100 км/ч у Mirai занимает девять секунд. В новой рекламе японская компания продемонстрировала еще один плюс Toyota Mirai: этот автомобиль способен ездить даже на продуктах жизнедеятельности коров.

По всей видимости, новый ролик является ответом «Тойоты» на нападки со стороны других производителей. К примеру, Элон Маск (Elon Musk) из Tesla Motors и Карлос Гон (Carlos Ghosn) из альянса Renault-Nissan весьма нелестно отзывались о проекте по созданию автомобиля, ездящего на водороде. Теперь японцы показали, что подходящее для легковушки топливо можно добывать даже из экскрементов крупного рогатого скота.

Продажи Toyota Mirai начнутся в США ближе к концу текущего года. Автомобиль будут сдавать в лизинг за 499 долларов в месяц либо продавать за 57 500 долларов без учета государственных субсидий, которые зависят от штата.

Пока японцы пытаются продвигать идею светлого водородного будущего, британцы не первый год приспосабливают технологии болидов «Формулы-1» к большим маршрутным автобусам. Казалось бы, что общего может быть у этих совершенно разных транспортных средств? Оказывается, таким элементом может стать маховик, который позволит накапливать кинетическую энергию, что снизит расход топлива и объем вредных выбросов. Год назад мы писали про британскую компанию GKN, которая приобрела Williams Hybrid Power Limited, подразделение Williams Grand Prix Engineering Limited (компании — владельца всемирно известной гоночной команды Williams). Основным интересом GKN стал так называемый «кинетический маховик», который предполагается использовать в автобусах. Теперь британцы поделились новыми достижениями своего амбициозного проекта.

Пока все идет намеченными ранее темпами. К концу 2021 года по Лондону будет ездить в общей сложности 500 автобусов, оснащенных углепластиковыми «кинетическими маховиками». Они будут раскручиваться во время торможения с помощью электромотора. При разгоне процесс будет запущен в обратном направлении. По расчетам инженеров, такой метод гораздо эффективнее обычного рекуперативного торможения, в котором используются аккумуляторные батареи.

По новым данным инженерной компании GKN, использование маховика позволит снизить вредные выбросы в окружающую среду на 50-75 процентов. Столь впечатляющие показатели стали доступны благодаря работе дизельного двигателя при постоянных оборотах — 1500 в минуту. Также использование инновационного маховика позволит снизить шум ускоряющегося автобуса.

Благодаря использованию углепластикового маховика в качестве источника энергии для электромотора можно будет сэкономить на двигателе внутреннего сгорания — он может стать компактнее и дешевле. По расчетам GKN, срок окупаемости инновационной системы составит всего два года. Также британцы рассказали о планах по дальнейшему совершенствованию своих автобусов. В перспективе в трансмиссию можно будет интегрировать небольшую батарею, которая вкупе с маховиком позволит проезжать несколько кварталов с полностью заглушенным двигателем внутреннего сгорания.

Преимущества и недостатки

Хотя использование матричной оптики, на первый взгляд, может показаться излишеством, технология имеет ряд неоспоримых преимуществ:

• увеличение комфорта и безопасности движения;
• не нужно думать о режиме работы освещения;
• отсутствие ослепляющего эффекта для встречных водителей;
• адаптивная работа света при движении по прямой и в поворотах;
• обнаружение пешеходов;
• динамические указатели повторов.

Из недостатков оптики можно выделить только высокую стоимость и использование технологии в автомобилях премиум-класса.

Матричные фары значительно упрощают езду на дорогах, особенно в плохих погодных условиях или ночью. Водителю не нужно переключать режимы работы света, а повороты становятся легкими и безопасными. Остается только дождаться, пока разработка дойдет до массового рынка и будет устанавливаться на все автомобили.
системах освещения автомобилей массово использовали только галогенные или газоразрядные лампы (ксенон). Позже производители начали переход на светодиодные источники света. Но настоящим п…» />

За какие продвинутые фары стоит переплачивать — Лайфхак

• Лайфхак
• Эксплуатация

Ксенон и даже светодиоды в фарах – уже прошлый век. Новые машины выходят на рынок с матричными и лазерными фарами. Но какой тип оптики действительно повышает безопасность в темное время суток, а какой – лишь маркетинговый ход и вымогание денег? Эксперты разобрались в вопросе.

Светлана Алеева

Пока автономные машины еще не бороздят мировые просторы в массовом порядке, за управление отвечает водитель. И по-прежнему один из главных параметров для него – хорошая видимость, поэтому в машине важными остаются такие характеристики как обзорность и освещенность дороги в темное время суток. Ради последнего пункта специалисты разложили по полочкам все типы фар.

Разложили в прямом смысле – эксперты американского Союза потребителей, обладающего собственными лабораториями и тестовыми полигонами, привели подробные характеристики всех современных автомобильных фар – от простых галогенок до лазерных, а также включая адаптивные и поворотные и даже штатные системы ночного видения.

Если верить рекламным описаниям, оптика нового типа способна обеспечить яркую освещенность, более длинный луч света – до 600 метров вперед и даже опознавание пешеходов и животных чуть ли не до того, как они появятся на дороге.

Новые технологии светотехники – настоящий рай для дизайнеров, которые теперь могут «рисовать» сложный и красивый «взгляд» машинам. Оптика становится фирменной «чертой узнавания» определенной марки или модели, далеко уйдя от однообразных кругов и квадратов. Зачастую новый рисунок оптики отличает обновленную модель от устаревшей.

И первый вывод экспертов, чтобы не мудрить и не таить: большинство продвинутых технологий в оптике не помогает видеть дальше – разве что ярче, чем нынешние галогенные фары. А вот стоят однозначно дороже.

АДАПТИВНЫЕ ФАРЫ ГОЛОВНОГО СВЕТА

Итак, речь идет о фарах-противотуманках по углам переднего бампера, которые зажигаются по одной в зависимости от поворота руля и подсвечивают таким образом поворот. Это неплохо как на парковке, так и в движении ночью по извилистой дороге. Однозначного мнения у экспертов Consumer Reports испытания поворотных фар не оставили, так что специалисты предлагают потребителям решать, нужна ли им такая платная опция.

 

КСЕНОН

Ксеноновые фары – больная тема для российских потребителей. Слишком много водителям пришлось сталкиваться с так называемым колхозным ксеноном, который слепит встречную полосу и вызывает море негативных эмоций, да и светит хуже штатного ксенона.

HID-фары – это оптика, в которой используется газ ксенон. Недостаточно даже линзованных фар для установки ксенона, так как если изначально фара не спроектирована под установку ксенона, там не учтены параметры нагрева, размер и яркость ксенона и галогена.

Но американские эксперты анализировали все же «правильный» штатный ксенон. Первый вывод: из-за более низких температур такие лампы служат дольше, но на выходе их замена обойдется сильно дороже. Но в целом особых преимуществ перед хорошей галогенной оптикой спецы не разглядели.

 

СВЕТОДИОДЫ

Фары, которые прозводители называет LED, могут быть световодные – когда горит пара диодов в трубочках, наполняя их светом, и светодиодные – когда вся линия представляет собой горящие диоды. Световоды применяются в основном в задних фонарях из-за меньшей стоимости.

История освещения у автомобилей начиналась с ацетиленовых горелок и обычных электрических фонарей, и с тех пор техника шагнула далеко вперед.  

Светодиоды имеют множество преимуществ: у них более высокая световая отдача, высокая механическая прочность и вибростойкость из-за отсутствия ламп накаливания, долгий срок службы, они не требуют времени на разогрев до полной яркости, они экологичны и компактны. Поэтому в автопромышленности они получают все большее распространение с выходом каждой новой модели. Но не дешевы.

Светодиоды активно используются для того самого «семейного» рисунка оптики. Однако полностью светодиодные фары, направленные на освещение дороги, могут бы как очень хороши – матричная на Mercedes-Benz S-Class, так и «слепее» галогенок – на Seat Leon, например.

МАТРИЧНЫЕ СВЕТОДИОДНЫЕ ФАРЫ

Матричные светодиодные фары – это уже следующий шаг. Причем доступный и для массового сегмента, так как появляются уже и на машинах гольф-класса. в блоках фар расположено больше десятка светодиодных сегментов, которые отвечают за дневные ходовые огни, ближний и дальний свет и боковую освещенность, регулируя интенсивность светового потока, направления и отключаясь группами по необходимости, например, чтобы не слепить встречных. Ориентироваться помогают камеры и датчики, «засекающие» встречную или попутную машину.

Матричный светодиодный свет очень хорош, но и весьма дорог. К слову, в США он запрещен. Но там и ксенон не сразу легализовался.

 

ЛАЗЕРНЫЕ ФАРЫ

Лазерные фары – последний тренд, доступный пока только в премиуме за неприличные деньги. По сути, такой свет пока предлагают только на BMW i8 и Audi R8, на подходе новые генерации седанов Audi. Неслучайно инженеры начали со спорткаров – лазерные фары светят вперед на 600 метров, что важно при быстром движении.

Синие лазерные лучи, попадая на специальную пластику, при помощи микрозеркала (Bosch) преобразуются в белые, которые и освещают путь. На малых скоростях фары освещают дорогу вширь, а на больших – «бьют» вперед. По словам производителей, по сравнению с матричными светодиодными фарами «лазеры» имеют большее динамическое разрешение и лучше освещают объекты в темноте. В США эта технология пока не разрешена законом.

СИСТЕМЫ НОЧНОГО ВИДЕНИЯ

Удивительные футуристичные системы военных разведок из кино добрались и до реальной жизни, причем довольно давно укрепились в серийных машинах – системы ночного видения. Конечно, пока речь идет только о люксовом сегменте.

При помощи камер и сенсоров машина засекает пешеходов и животных сильно заранее, их изображения появляются на центральном мониторе автомобиля. Иногда даже в случае обнаружения «объектов» машина сама зажигает дополнительное освещение или подмигивает, чтобы «спугнуть» тех с дороги или даже «нарисовать» освещенный путь отступления. Но все же картинка на мониторе отвлекает водителя непосредственно от дороги.

Подпишитесь на канал «Автовзгляд»:

• Telegram
• Яндекс.Дзен

безопасность дорожного движения, технология

Матрица

ABCD, объяснение RP Photonics Encyclopedia; матрица переноса лучей

Главная	Викторина	)»> Руководство покупателя
Поиск	Категории	Глоссарий	Реклама

Прожектор фотоники

Учебники

Показать статьи A-Z

Примечание: поле поиска по ключевому слову статьи и некоторые другие функции сайта требуют Javascript, который, однако, отключен в вашем браузере.

Обратитесь в RP Photonics за советом о том, как рассчитать матрицы ABCD, какое программное обеспечение использовать и т. д. Для таких целей у RP Photonics есть программное обеспечение RP Resonator .

Матрица ABCD [1] представляет собой матрицу 2 на 2, связанную с оптическим элементом, которую можно использовать для описания воздействия элемента на лазерный луч. Его можно использовать как в

лучевой оптике , где распространяются геометрические лучи, так и для распространения гауссовых лучей. Для расчетов матрицы ABCD всегда требуется параксиальное приближение, т. Е. Используемые углы луча или углы расхождения должны оставаться небольшими, чтобы расчеты были точными.

Лучевая оптика

Первоначально концепция была разработана в геометрической оптике для расчета распространения световых лучей с некоторым поперечным смещением r и углом смещения θ от базовой оси (рис. 1). Пока вовлеченные углы достаточно малы (→ параксиальная аппроксимация ), существует линейная зависимость между координатами r и θ до и после оптического элемента. Затем можно использовать следующее уравнение для расчета того, как эти параметры изменяются оптическим элементом:

Рисунок 1: Определение r и θ до и после оптической системы.

, где заштрихованные величины (слева) относятся к лучу после прохождения оптического компонента. Матрица ABCD (также называемая матрицей переноса лучей ) является характеристикой каждого оптического элемента.

Например, тонкая линза с фокусным расстоянием f имеет следующую матрицу ABCD:

Это показывает, что смещение r остается неизменным, тогда как угол смещения θ изменяется пропорционально р .

Распространение в свободном пространстве на расстояние d связано с матрицей

, которая показывает, что угол остается неизменным, тогда как смещение луча увеличивается или уменьшается в зависимости от угла.

Другие примеры для матриц ABCD приведены ниже.

Можно показать, что определитель матрицы ABCD ( A D − B C ) всегда должен быть равен 1, если показатель преломления одинаков на входе и выходе; в противном случае это входной показатель преломления, деленный на выходной показатель преломления.

Модифицированные матрицы

Для ситуаций, когда лучи распространяются через диэлектрические среды, удобно использовать модифицированный вид векторов луча, в котором нижняя составляющая (угол) умножается на показатель преломления:

Это может несколько упростить ABCD матрицы для определенных ситуаций. Во многих случаях оптики в свободном пространстве это не имеет значения, поскольку лучи рассматриваются только в положениях в воздухе, где n &приблизительно;  1. Однако это затрагивает, например, уравнения для интерфейсов между различными средами.

Определитель такой модифицированной матрицы ABCD ( A D − B C ) всегда равен 1.

Распространение гауссовых лучей

Матрицы

ABCD также можно использовать для расчета влияния оптических элементов на параметры гауссова пучка. Подходящей величиной для этой цели является комплексный параметр q , который содержит информацию как о радиусе пучка w , так и о радиусе кривизны R волновых фронтов:

Следующее уравнение показывает, как0050 q параметр изменен оптическим элементом:

ABCD Матрицы важных оптических элементов

В следующем списке приведены матрицы ABCD часто используемых оптических элементов.

Воздушное пространство длиной d :

(Для распространения в прозрачной среде длина d должна быть разделена на показатель преломления n , если используется вышеупомянутое модифицированное определение, где нижняя компонента ( угол) умножается на показатель преломления.)

Линза с фокусным расстоянием f (где положительное значение f применяется для фокусирующей линзы):

Изогнутое зеркало с радиусом кривизны R (>0 для вогнутого зеркала), угол падения θ в горизонтальной плоскости:

с R _e  =  R  cos θ в тангенциальной плоскости (горизонтальное направление) и R _e  =  R  cos/s в вертикальной плоскости.

Гауссов канал:

, где радиально изменяющийся показатель преломления равен

, и используется измененное определение векторов луча – с углом, умноженным на показатель преломления (см. выше).

В различных учебниках (см. , например, [4]) указаны матрицы ABCD для других типов оптических компонентов.

Объединение нескольких оптических элементов

Если луч проходит через несколько оптических элементов (включая любые воздушные пространства между ними), это означает, что вектор ( r θ ) последовательно умножается на различные матрицы. Вместо этого можно использовать одну матрицу, которая является матричным произведением всех одиночных матриц. Обратите внимание, что первый оптический элемент должен быть в правой части этого произведения — матричные умножения не коммутативны, и то же самое верно для оптических элементов.

Пример:

• комбинированная матрица для длины распространения в свободном пространстве с расстоянием d , за которой следует линза с фокусным расстоянием f :

• комбинированная матрица для объектива с фокусным расстоянием f , за которым следует длина распространения в свободном пространстве с расстоянием d :

Типичные области применения

Вот некоторые типичные применения матричного алгоритма ABCD:

• Часто бывает интересно, как лазерный луч распространяется через некоторую оптическую установку. Можно рассчитать как геометрический путь луча, так и эволюцию радиуса луча.
• Изменения параметров пучка за один полный обход резонатора можно описать с помощью матрицы ABCD. Моды поперечного резонатора затем могут быть получены из матричных компонентов.
• Расширенный алгоритм, включающий матрицу ABCDEF (матрица 3 на 3 с некоторыми постоянными компонентами), может быть использован для расчета чувствительности юстировки лазерного резонатора [3].

Матричный метод ABCD не следует путать с другим матричным методом для расчета свойств отражения и пропускания диэлектрических многослойных покрытий.

Вопросы и комментарии от пользователей

Здесь вы можете задать вопросы и комментарии. Если они будут приняты автором, они появятся над этим абзацем вместе с ответом автора. Автор принимает решение о принятии на основе определенных критериев. По существу, вопрос должен представлять достаточно широкий интерес.

Пожалуйста, не вводите здесь личные данные; в противном случае мы бы удалили его в ближайшее время. (См. также нашу декларацию о конфиденциальности.) Если вы хотите получить личную обратную связь или консультацию от автора, свяжитесь с ним, например. по электронной почте.

Ваш вопрос или комментарий:

Проверка на спам:

  (Пожалуйста, введите сумму тринадцати и трех в виде цифр!)

Отправляя информацию, вы даете свое согласие на возможную публикацию ваших материалов на нашем веб-сайте в соответствии с нашими правилами. (Если вы позже отзовете свое согласие, мы удалим эти материалы.) Поскольку ваши материалы сначала просматриваются автором, они могут быть опубликованы с некоторой задержкой.

Библиография

[1]	H. Kogelnik и T. Li, «Лазерные лучи и резонаторы», Appl. Опц. 5 (10), 1550 (1966), doi:10.1364/AO.5.001550
[2]	П. А. Беланже, “Распространение пучка и матрицы лучей ABCD”, Опт. лат. 16 (4), 196 (1991), doi:10.1364/OL.16.000196
[3]	О. Е. Мартинес, «Матричный формализм для дисперсионных лазерных резонаторов», IEEE J. Quantum Electron. 25 (3), 296 (1989), doi:10.1109/3.18543
[4]	A. E. Siegman, Lasers , University Science Books, Mill Valley, CA (1986)

(Предложите дополнительную литературу!)

См. также: геометрическая оптика, параксиальное приближение, гауссовы пучки, моды резонатора, конструкция резонатора, флуктуации наведения луча
и др. статьи в категориях общая оптика, методы

Если вы хотите разместить ссылку на эту статью на каком-либо другом ресурсе (например, на своем сайте, в социальных сетях, на дискуссионном форуме, в Википедии), вы можете получить необходимый код здесь.

HTML-ссылка на эту статью:

  
 Статья о матрице ABCD 
 в  
 Энциклопедия RP Photonics 

С изображением для предварительного просмотра (см. поле чуть выше):

   rp-photonics.com/abcd_matrix.html"> 
  alt="article"> 

Для Википедии, например. в разделе «==Внешние ссылки==»:

 * [https://www.rp-photonics.com/abcd_matrix.html 
 статья о матрице ABCD в энциклопедии RP Photonics] 

MATRIX OPTICS

MATRIX OPTICS

 

Телескопы, микроскопы, камеры и многие другие оптические инструменты имеют общий дизайн, который не изменился со времен Галилео. Лучи света входят в один конец систему, ударить по линзе или зеркалу, изменить направление, проехать определенное расстояние, затем столкнуться с другой линзой или зеркалом, снова изменить направление и так далее. В конце концов лучи попадают на пленку или фотодетектором и фиксируются химическими или электронными средствами

 

Выяснение того, как пробиваются все лучи света через оптическое устройство — сложная задача, но она может быть эффективно формулируются с использованием матриц. Мы можем тогда использовать наши знания о матрицах для решения практических задач, таких как расположение изображений. и увеличения. Матрица формулировка предполагает, что все лучи почти параллельны заданному оптическая ось проходит по всей длине устройства, а все линзы тонкие по сравнению с расстоянием между линзами. Что ж, представь, что нет ни зеркал, ни призм, меняющих направление. оптической оси на большие углы.

 

Когда мы говорим о луче, мы имеем в виду путь, который является прямым линия между линзами, и которая может менять направление при прохождении через объектив. Если он находится на высоте Yl с уклоном Sl на левом конце безлинзового интервала длины d, затем на правом конце этого интервала он по-прежнему будет иметь тот же наклон Sr = Sl, но высота изменится на d*Sl, т. е. Yr=Yl+d*Sl. И наоборот, когда луч проходит через линзу, его высота остается неизменной. Yr=Yl, но его наклон изменяется на величину, пропорциональную высоте: Sr=Sl-Yl/f. Величина f является фокусным расстоянием линзы, и обычно она положительна для выпуклой линзы и отрицательна для вогнутой. линза (при условии, что показатель преломления больше 1!).

 

 

. отношения удобно выражать в терминах матриц. Но истинная сила матричной формулировки появляется только тогда, когда вы начинаете ставить несколько линз вдоль оси в разных интервалы. Свойства такого оптическую систему можно вывести простым перемножением отдельных матриц (в правильном порядке), соответствующие отдельным интервалам и линзам. Интересно, что мы склонны рисовать оптические пути, как указано выше, с лучами, распространяющимися слева направо. Матрицы, представляющие эти оптические компоненты должны быть умножены в обратном порядке, справа налево.

В качестве первого примера рассмотрим случай одиночного выпуклая линза с точечным источником света на расстоянии a слева и экраном на расстоянии b справа.

 

В источнике все лучи имеют одинаковое значение Y (назовем его Y0), а наклон S0 может принимать различные значения. (Математически S0 может быть любым положительным или отрицательное число; практически существует конечный диапазон, для которого луч фактически попадает в линзу конечного диаметра.) Распространение слева от линзы равно

 

, затем проходящий через линзу на ,

 

 

затем распространяется вправо на . Или все вместе:

 

 

 

 

 

Теперь то, как я нарисовал, лучи света источник снова сходятся в одной точке экрана, другими словами высота Y3, при которой лучи попадают на экран, не зависит от наклона S0 с которые оставили источник света. Глядя на перемноженную матрицу, вы видите, что это может произойти только если верхняя правая запись равна нулю, т.е. a + б = аб/е . Вы можете быть больше знаком с этой формулой как , относящийся к объекту расстояние a, расстояние изображения b и фокусное расстояние объектива f . (Я начал эту задачу, представляя себе только один источник света, но в на самом деле этот аргумент применим к каждой отдельной светоизлучающей точке в сложный реальный объект.) Когда это соотношение выполняется, вы можете считать Y3 = (1 b/f )Y0, что указывает на то, что увеличение изображения составляет (1 б/ф ). Этот фактор может быть как положительным, так и отрицательный; отрицательное значение означает, что изображение перевернуто, т.е. перевернуто.

 

У меня есть еще примеры, но я позволю вам разобраться с ними как домашнее задание.

Информационный век в оптике: Измерение матрицы пропускания

Точка зрения

8 марта 2010 г. • Физика 3, 22

Прохождение света через неупорядоченную среду описывается в микроскопических деталях высокоразмерной матрицей. Теперь исследователи напрямую измерили эту матрицу пропускания, предложив новый подход к управлению распространением света.

Рис. 1: Два оптических элемента, полностью охарактеризованные своей матрицей пропускания, которая связывает фронт падающей волны с фронтом прошедшей волны. В случае тонкой линзы преобразование волнового фронта описывается матрицей 2×2, оперирующей вектором, описывающим кривизну волнового фронта [27]. Для более сложных элементов, таких как кубик сахара, матрица передачи работает на основе поперечных мод, которые очень велики. Полное знание матрицы пропускания позволяет неупорядоченным материалам фокусировать свет как линзы. Два оптических элемента полностью характеризуются своей матрицей пропускания, которая связывает фронт падающей волны с прошедшим. В случае тонкой линзы преобразование волнового фронта описывается матрицей 2×2, оперирующей вектором d. .. Подробнее Рис. 1: Два оптических элемента, полностью охарактеризованных матрицей пропускания, которая связывает фронт падающей волны с фронтом прошедшей волны. В случае тонкой линзы преобразование волнового фронта описывается матрицей 2×2, оперирующей вектором, описывающим кривизну волнового фронта [27]. Для более сложных элементов, таких как кубик сахара, матрица передачи работает на основе поперечных мод, которые очень велики. Полное знание матрицы пропускания позволяет неупорядоченным материалам фокусировать свет как линзы.

×

Оптические элементы, такие как линзы и поляризаторы, используются для изменения распространения света. Преобразования фронта оптической волны, которые осуществляют эти элементы, описываются простыми и прямолинейными матрицами пропускания (рис. 1). Формализм матриц передачи также используется для микроскопического описания передачи через более сложные оптические системы, включая непрозрачные материалы, такие как слой краски, в котором сильно рассеивается свет. Микроскопическое описание этого процесса рассеяния требует матрицы пропускания с огромным количеством элементов. Себастьян Попофф, Жоффруа Лерозе, Реми Карминати, Матиас Финк, Клод Боккара и Сильвен Жиган из Института Ланжевена в Париже теперь сообщают в Physical Review Letters экспериментальный подход к микроскопическому измерению матрицы пропускания света [1]. Знание матрицы пропускания обещает более глубокое понимание транспортных свойств и позволяет точно контролировать распространение света через сложные фотонные системы.

На первый взгляд непрозрачные неупорядоченные материалы, такие как бумага, краска и биологические ткани, полностью отличаются от линз и других прозрачных оптических элементов. В неупорядоченных материалах вся информация во фронте волны теряется из-за многократного рассеяния. Распространение света в таких материалах очень успешно описывается диффузионным подходом, при котором отбрасывается информация о фазе и рассматривается только интенсивность. Важный ключ к тому, что информация о фазе очень актуальна в неупорядоченных системах, был дан наблюдением слабой локализации фотонов в диффузных образцах [2,3]. Даже чрезвычайно длинные световые пути создают конструктивную интерференцию в точном направлении обратного рассеяния, интерференционный эффект, который можно наблюдать почти во всех системах многократного рассеяния. Интерференция в сочетании с очень сильным рассеянием даже остановит диффузию, когда условия будут подходящими для локализации Андерсона [4]. Поскольку световые волны не теряют своих свойств когерентности даже после тысяч актов рассеяния, перенос света через неупорядоченный материал является вовсе не диссипативным, а когерентным, с высокой информационной емкостью [5].

Распространяющаяся монохроматическая световая волна характеризуется формой своего волнового фронта. Выбрав подходящий базис, фронт волны, падающей на образец, можно разложить на ортогональные моды. Типичным выбором для этого базиса мод являются ортогональные моды волновода или базис плоских волн в свободном пространстве. Поскольку необходимо учитывать только распространяющиеся волны, количество мод конечно, и они составляют основу, на которой записывается матрица передачи. Матрица передачи выборки определяет амплитуду передаваемого поля для каждой комбинации падающей и передаваемой мод. С теоретической точки зрения матрицы передачи являются полезными инструментами для понимания корреляций при переносе света и других волн. Большое понимание свойств матрицы передачи было получено в рамках мезоскопической теории переноса [6]. Матрица пропускания играла менее важную роль в экспериментах из-за ее чрезвычайно высокой размерности: это матрица N × N комплексных чисел, где N представляет собой количество мод падающего (и проходящего) светового поля, связанного с образцом. Каждая падающая мода соответствует дискретному углу падения, а количество разрешаемых дискретных углов равно N=2πA/λ2[7], где A — площадь освещаемой поверхности, λ — длина волны, а коэффициент 2 учитывает две ортогональные поляризации. Следовательно, образец площадью 1 мм2 имеет около миллиона поперечных оптических мод. До недавнего времени измерение матрицы с соответствующим большим количеством элементов было за пределами технических возможностей. Прогресс в технологии цифровых изображений позволил теперь измерять и обрабатывать такие большие объемы данных. В частности, пространственные модуляторы света — управляемые компьютером элементы, которые контролируют фазу в каждом пикселе двумерного волнового фронта — в настоящее время совершают цифровую революцию в оптике и лежат в основе эксперимента Попоффа и его коллег.

В своем эксперименте они использовали пространственный модулятор света для точного управления волновым фронтом монохроматического лазерного луча, что позволило им работать с различными падающими модами сильно неупорядоченного образца. Умело используя часть проходящего света в качестве эталона фазы, они смогли зафиксировать информацию об амплитуде и фазе на двумерной ПЗС-матрице размером 16×16 пикселей. Благодаря этому параллельному обнаружению они измерили 164 элемента матрицы передачи всего за 162 шага. Их метод позволяет глубоко охарактеризовать перенос света через мутные среды, что позволяет им контролировать распространение света, как они продемонстрировали, превратив свой образец в элемент фокусировки и обнаружения. Чтобы сфокусировать свет, они использовали информацию в матрице пропускания для построения волновых фронтов, которые после рассеяния на образце образовывали плотный фокус. Их подход является более гибким, чем эксперименты с «непрозрачными линзами» первого поколения [8], поскольку данные для создания фокуса в любом желаемом положении уже находятся в матрице передачи. Для обнаружения объектов, расположенных перед рассеивающим образцом, они сравнивали проходящее поле с информацией, хранящейся в матрице пропускания.

Прямой доступ к отдельным элементам матрицы позволяет выполнять их статистический анализ. Статистические свойства матрицы передачи описываются с помощью теории случайных матриц, аналитического подхода, который фокусируется на симметрии и законах сохранения, а не на подробном взаимодействии (для введения см. [9] и ссылки в ней). Например, элементы матрицы передачи являются коррелированными из-за того, что ни один из матричных элементов или сингулярных значений никогда не может быть больше единицы, так как в этом случае будет передано более 100% падающей мощности [10]. Однако эта корреляция неуловима и может наблюдаться только при измерении всей матрицы передачи.

В текущих экспериментах количество измеренных матричных элементов впечатляет (65536), однако матрица пропускания полной площади образца еще больше. Тем не менее, матрица, измеренная Popoff et al. было достаточно большим, чтобы проверить важное базовое предсказание теории случайных матриц: гистограмма его сингулярных значений должна иметь своеобразную форму четверти круга [11,12]. Тот факт, что данные следуют этому закону четверти окружности, означает, что матричные элементы не имеют существенной корреляции, что является хорошим показателем того, что экспериментальная процедура не вводит ложных корреляций. Измеряя значительно большие матрицы, можно выявить внутренние корреляции. В достаточно большой матрице сингулярное распределение будет отклоняться от закона четверти окружности и сходиться к бимодальному распределению, состоящему в основном из полностью передающих (открытых) и полностью отражающих (закрытых) каналов (обзоры см. в [13–15]). ]). Используя информацию в такой матрице, можно будет создать идеальный волновой фронт, который связывается только с открытыми каналами и проходит через непрозрачную среду на полных 100%.

Еще одним интересным экспериментом будет измерение матрицы пропускания образцов с экстремальным беспорядком. Когда трехмерные образцы приближаются к порогу локализации Андерсона, матрицы пропускания дадут прямое представление о локализованном режиме, где моды проходящего света должны иметь интригующие свойства [13,16-19]. Точно так же было бы чрезвычайно интересно изучить матрицу пропускания так называемого стекла Леви [20], в котором свет распространяется по сильно модифицированному закону диффузии, или фотонных кристаллов, обладающих неизбежным беспорядком [21] в дополнение к сложная ленточная структура.

В относительно прозрачных материалах трансмиссионная матрица может быть использована для получения томографической реконструкции образца [22], которая может быть использована для отслеживания процессов внутри живых клеток. Пока неясно, можно ли этот подход распространить на материалы с более сильным рассеянием, но есть надежда, что информацию можно будет получить изнутри непрозрачной биологической ткани [23, 24]. Алгоритмы получения информации о скрытых целях из ультразвуковых измерений (см., например, [25]) могут быть перенесены в оптику.

Подход Попоффа и его коллег знаменует собой начало очень увлекательного пути к более глубокому пониманию легкового транспорта. Технический прогресс позволит измерять все более и более крупные матрицы, содержащие всю доступную информацию об образцах. Текущие разработки в области анализа случайных матриц (см., например, [26]) позволят разобраться в этих огромных объемах информации. Когда информация в матрице передачи полностью известна, любая неупорядоченная система становится качественным оптическим элементом (рис. 1). С технологической точки зрения это имеет большие перспективы: вполне возможно, что неупорядоченные рассеивающие материалы вскоре станут предпочтительными нанооптическими элементами.

Ссылки

1. S.M. Popoff, G. Lerosey, R. Carminati, M. Fink, A.C. Boccara, and S. Gigan, Phys. Преподобный Летт. 104 , 100601 (2010)
2. M.P. van Albada and A. Lagendijk, Phys. Преподобный Летт. 55 , 2692 (1985)
3. P. E. Wolf and G. Maret, Phys. Преподобный Летт. 55 , 2696 (1985)
4. A. Lagendijk, B. van Tiggelen, and D.S. Wiersma, Phys. Today 62 , №8, 24 (2009)
5. Скипетров С.Е. // Физ. Ред. Д 67 , 036621 (2003)
6. C.W.J. Beenakker, Rev. Mod. физ. 69 , 731 (1997)
7. Р. П. Фейнман, Р. Б. Лейтон и М. Сэндс, Фейнмановские лекции по физике , Vol. 3 (Addison-Wesley, New York, 1965) [Amazon][WorldCat]
8. I. M. Vellekoop and AP Mosk, Opt. лат. 32 , 2309 (2007)
9. P. J.Forrester, N.C.Snaith, and J.J.M.Verbaarschot, J.Phys. A 36 , R1 (2003)
10. J. Pendry, A. MacKinnon, and A. Pretre, Physica A 168 , 400 (1990)
11. В. А. Марченко, Л. А. Пастур, Матем. СССР-Сборник 1 , 457 (1967)
12. Э. П. Вигнер, SIAM Rev. Today 61 , № 9, 20 (2008)
13. C.W.J.Beenakker, arXiv:0904.1432 (2009)
14. C.M. Soukoulis and E.N. Economou, Phys. Преподобный Летт. 52 , 565 (1984)
15. А. А. Чабанов, М. Стойчев, А. З. Генак, Природа 404 , 6780 (2000)
16. M. Störzer, P. Gross, C. M. Aegerter, and G. Maret, Phys. Преподобный Летт. 96 , 063904 (2006)
17. S. Faez, A. Strybulevych, J.H. Page, A. Lagendijk, and B.A. van Tiggelen, Phys. Преподобный Летт. 103 , 155703 (2009)
18. P. Barthelemy, J. Bertolotti, and D.S. Wiersma, Nature 453 , 495 (2008)
19. A.F. Koenderink, A. Lagendijk. Vos, and W. L. Phys. B 72 , 153102 (2005)
20. W. Choi и др. , Нац. Methods 4 , 717 (2007)
21. Z. Yaqoob, D. Psaltis, M.S. Feld, and C. Yang, Nature Photon. 2 , 110 (2008)
22. I.M.Vellekoop, E.G.van Putten, A.Lagendijk, and A.P.Mosk, Opt. Express 16 , 67 (2008)
23. M. Fink, Phys. Today 50 , No. 3, 34 (1997)
24. A. Edelman and N. Raj Rao, Acta Numerica 14 , 233 (2005)
25. H. Kogelnik and T. Li, Proc. IEEE 54 , 1312 (1966)

Об авторах

Эльберт ван Путтен работает над докторской диссертацией. в группе комплексных фотонных систем Института нанотехнологий MESA+ Университета Твенте в Нидерландах. Его исследования сосредоточены на получении активного контроля над распространением света в сильно неупорядоченных материалах.

Аллард Моск — адъюнкт-профессор группы сложных фотонных систем Института нанотехнологий MESA+ Университета Твенте в Нидерландах. Он получил докторскую степень. в 1999 из Амстердамского университета, где он проводил экспериментальные исследования квантовых газов. В настоящее время он работает над методами контроля как излучения, так и распространения света в сложных нанофотонных средах. Он получает стипендию Vidi от Нидерландской организации научных исследований (NWO).

---

Читать PDF Читать PDF

Предметные области

Оптика

Статьи по теме

Астрофизика

Мини-интерферометры предлагают впечатляющую чувствительность

15 сентября 2022 г.

Датчик, содержащий миниатюрные интерферометры, может помочь астрономам обнаруживать гравитационные волны, испускаемые некоторыми слияниями черных дыр. Подробнее »

Физика конденсированного состояния

Атомный массив форм стробоскопического света

14 сентября 2022 г.

Оптический пинцет со стробоскопическим изгибом может улавливать холодные атомы в решетках любой формы. Подробнее »

Атомная и молекулярная физика

Интерферометрическое исследование молекулярного магнетизма

12 сентября 2022 г.

Интерферометр материи-волны может исследовать магнетизм широкого спектра видов, от отдельных атомов до очень больших слабомагнитных молекул. Подробнее »

Другие статьи

Анализ матрицы переноса лучей

Анализ матрицы переноса лучей (также известный как матричный анализ ABCD) — это тип метода трассировки лучей, используемый при разработке некоторых оптических систем, в частности лазеров. Он включает в себя построение матрицы переноса лучей, которая описывает оптическую систему; затем отслеживание пути света через систему может быть выполнено путем умножения этой матрицы на вектор, представляющий световой луч.

В методике, описанной ниже, используется параксиальное приближение лучевой оптики, т. е. предполагается, что все лучи проходят под малым углом (θ) и на небольшом расстоянии (x) относительно оптической оси системы. Аппроксимация действительна до тех пор, пока sin(θ)≈θ (где θ измеряется в радианах). [Точный метод отслеживания меридиональных лучей доступен, в частности, на org/etop/1991/389_1.pdf>.

Определение матрицы переноса лучей

Метод трассировки лучей основан на двух опорных плоскостях, называемых входной и выходной плоскостями, каждая из которых перпендикулярна оптической оси системы. Без ограничения общности определим оптическую ось так, чтобы она совпадала с осью z фиксированной системы координат. Луч света входит в систему, когда луч пересекает входную плоскость на расстоянии x ₁ от оптической оси при движении в направлении, которое составляет угол θ ₁ с оптической осью. На некотором расстоянии луч пересекает выходную плоскость, на этот раз на расстоянии x ₂ от оптической оси под углом θ ₂ . n ₁ и n ₂ — показатели преломления среды во входной и выходной плоскостях соответственно.

Эти величины связаны выражением

\( {x_2 \choose \theta_2} = \begin{pmatrix} A & B \\ C & D \end{pmatrix}{x_1 \choose \theta_1}, \)

где

\( A = {x_2 \over x_1 } \bigg|_{\theta_1 = 0} \qquad B = {x_2 \over \theta_1 } \bigg|_{x_1 = 0},\)

и

\( C = {\theta_2 \over x_1} \bigg|_{\theta_1 = 0} \qquad D = {\theta_2 \over \theta_1} \bigg|_{x_1 = 0}. \)

Это связывает векторы лучей во входной и выходной плоскостях с помощью матрицы переноса лучей (RTM) M, которая представляет оптическую систему между двумя эталонными плоскостями. Аргумент термодинамики, основанный на излучении черного тела, можно использовать, чтобы показать, что определяющим фактором RTM является отношение показателей преломления:

\( \det(\mathbf{M}) = AD — BC = { n_1 \over n_2 }. \)

В результате, если входная и выходная плоскости расположены в одной среде или в двух разных средах с одинаковыми показателями преломления, то определитель M просто равен 1.

Аналогичный метод можно использовать для анализа электрических цепей. См. Сети с двумя портами.
Некоторые примеры

Например, если между двумя плоскостями есть свободное пространство, матрица переноса лучей имеет вид:

\( \mathbf{S} = \begin{pmatrix} 1 & d \\ 0 & 1 \end{pmatrix} , \)

где d — разделительное расстояние (измеренное вдоль оптической оси) между двумя эталонными самолеты. Таким образом, уравнение переноса лучей принимает вид:

\( {x_2 \выбрать \theta_2} = \mathbf{S}{x_1 \выбрать \theta_1} , \)

и это связывает параметры двух лучей как:

\ ( \begin{matrix} x_2 & = & x_1 + d\theta_1 \\ \theta_2 & = & \theta_1 \end{matrix} \)

Другой простой пример — тонкая линза. Его RTM задается следующим образом:

\( \mathbf{L} = \begin{pmatrix} 1 & 0 \\ \frac{-1}{f} & 1 \end{pmatrix} , \)

где f фокусное расстояние объектива. Чтобы описать комбинации оптических компонентов, матрицы переноса лучей можно перемножить, чтобы получить общую RTM для составной оптической системы. Для примера свободного пространства длины d, за которым следует линза с фокусным расстоянием f:

\( \mathbf{L}\mathbf{S} = \begin{pmatrix} 1 & 0 \\ \frac{-1}{ f} & 1\end{pmatrix} \begin{pmatrix} 1 & d \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & d \\ \frac{-1}{f} & 1- \frac{d}{f} \end{pmatrix} . \)

Обратите внимание, что, поскольку умножение матриц не является коммутативным, это не то же самое RTM, что и для линзы, за которой следует свободное пространство:

\( \mathbf{SL} = \begin{pmatrix} 1 & d \ \ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{-1}{f} & 1\end{pmatrix} = \begin{pmatrix} 1-\frac{d}{f } & d \\ \frac{-1}{f} & 1 \end{pmatrix} . \)

Таким образом, матрицы должны быть упорядочены соответствующим образом. Другие матрицы могут быть построены для представления интерфейсов со средами с разными показателями преломления, отражения от зеркал и т. д.
Таблица матриц переноса лучей

для простых оптических компонентов

Элемент	Матрица	Замечания
Распространение в свободном пространстве или в среде с постоянным показателем преломления	\( \begin{pmatrix} 1 & d\\ 0 & 1 \end{pmatrix} \)	d = расстояние
Преломление на плоской границе раздела	\( \begin{pmatrix} 1 & 0 \\ 0 & \frac{n_1}{n_2} \end{pmatrix} \)	n 1 = начальный показатель преломления n 2 = окончательный показатель преломления.
Преломление на искривленной границе раздела	\( \begin{pmatrix} 1 & 0 \\ \frac{n_1-n_2}{R \cdot n_2} & \frac{n_1}{n_2} \end{pmatrix} \)	R = радиус кривизны, R > 0 для выпуклости (центр кривизны после поверхности раздела) n 1 = начальный показатель преломления n 2 = окончательный показатель преломления.
Отражение от плоского зеркала	\( \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \)
Отражение от изогнутого зеркала	\( \begin{pmatrix} 1 & 0 \\ -\frac{2}{R} & 1 \end{pmatrix} \)	R = радиус кривизны, R > 0 для вогнутости
Тонкая линза	\( \begin{pmatrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{pmatrix} \)	f = фокусное расстояние линзы, где f > 0 для выпуклой/положительной (собирающей) линзы. Действительно только в том случае, если фокусное расстояние намного больше толщины линзы.
Толстая линза	\( \begin{pmatrix} 1 & 0 \\ \frac{n_2-n_1}{R_2} & 1 \end{pmatrix} \begin{pmatrix} 1 & \frac{t}{n_2} \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{n_1-n_2}{R_1} & 1 \end{pmatrix} \)	n 1 = показатель преломления вне линзы. n 2 = показатель преломления самой линзы (внутри линзы). R 1 = Радиус кривизны первой поверхности. R 2 = Радиус кривизны второй поверхности. t = толщина линзы (без учета толщины изогнутых частей. Если требуется общая толщина, общая толщина будет равна t + толщина обеих изогнутых частей.
Одинарная прямоугольная призма	\( \begin{pmatrix} k & \frac{d}{nk} \\ 0 & \frac{1}{k} \end{pmatrix} \)	\( k = (cos\psi/cos\phi) \) — коэффициент расширения луча, где \( \phi \) — угол падения, \psi — угол преломления, d = длина пути призмы, n = показатель преломления материала призмы. Эта матрица применяется для выхода ортогонального луча.

Стабильность резонатора

RTM-анализ особенно полезен при моделировании поведения света в оптических резонаторах, таких как те, которые используются в лазерах. В простейшем случае оптический резонатор состоит из двух одинаковых обращенных друг к другу зеркал со 100%-ной отражательной способностью и радиусом кривизны R, отстоящих друг от друга на некотором расстоянии d. Для целей трассировки лучей это эквивалентно серии идентичных тонких линз с фокусным расстоянием f=R/2, каждая из которых отделена от следующей на длину d. Эта конструкция известна как канал, эквивалентный линзе, или волновод, эквивалентный линзе. RTM каждой секции волновода, как и выше,

\( \mathbf{M} =\mathbf{L}\mathbf{S} = \begin{pmatrix} 1 & d \\ \frac{-1}{f} & 1-\frac{d}{f } \end{pmatrix} .\)

RTM-анализ теперь можно использовать для определения устойчивости волновода (и, что то же самое, резонатора). То есть можно определить, при каких условиях свет, проходящий по волноводу, будет периодически перефокусироваться и оставаться внутри волновода. Для этого мы можем найти все лучевые векторы, у которых выход каждой секции волновода равен входному вектору, умноженному на некоторую действительную или комплексную константу λ:

\( {x_2 \выбрать \theta_2} = \lambda {x_1 \выбрать \theta_1} . \)

Это дает:

\( \mathbf{M}{x_1 \выбрать \theta_1} = \lambda {x_1 \выберите \theta_1} , \)

, которое является уравнением с собственным значением:

\( \left[ \mathbf{M} — \lambda\mathbf{I} \right] {x_1 \choose \theta_1} = 0 \)

, где I — единичная матрица 2×2.

Упрощая, имеем

\( \operatorname{det} \left[ \mathbf{M} — \lambda\mathbf{I} \right] = 0 \) 9{ \pm i \phi } , \)

где

\( \cos(\phi) = \operatorname{Re} \{ \lambda \} = g = {\operatorname{tr}(\mathbf{M} ) \over 2 } = 1 — { d \over 2 f } \)

Технику можно обобщить для более сложных резонаторов путем построения подходящей матрицы M для резонатора из матриц присутствующих компонентов.
Матрицы переноса лучей для гауссовых лучей

Матричный формализм также полезен для описания гауссовых лучей. Если у нас есть гауссов пучок с длиной волны \( \lambda_0 \), радиусом кривизны R, размером пятна луча w и показателем преломления n, можно определить комплексный параметр луча q следующим образом: 92} . \)

Этот луч можно распространить через оптическую систему с заданной матрицей переноса луча, используя уравнение:

\( {q_2 \выбрать 1} = k \begin{pmatrix} A & B \\ C & D \ end{pmatrix} {q_1 \choose 1} , \)

где k — константа нормализации, выбранная так, чтобы второй компонент лучевого вектора оставался равным 1. Используя матричное умножение, это уравнение расширяется как

\( q_2 = k (Aq_1 + B) \, \)

и

\( 1 = k(Cq_1 + D) \, \)

Деление первого уравнения на второе устраняет константу нормализации:

\( q_2 =\frac{Aq_1+B}{Cq_1+D}, \)

Последнее уравнение часто бывает удобно выразить в обратной форме:

{ 1 \ над q_2 } = { C + D/q_1 \ над A + B/q_1 } . \)

См. также

Метод трансфер-матрицы (оптика)
Двухпортовая сеть
Линейное каноническое преобразование

Ссылки

Бахаа Э. А. Салех и Малвин Карл Тейч (1991). Основы фотоники. Нью-Йорк: Джон Уайли и сыновья. Раздел 1.4, стр. 26 — 36.
А. Джеррард Б. Берч (1975). Матричные методы в оптике. Нью-Йорк: Джон Уайли и сыновья.
Ф. Дж. Дуарте (2003). Перестраиваемая лазерная оптика. Нью-Йорк: Эльзевир-Академик. Глава 6.

Внешние ссылки

Толстые линзы (Матричные методы)
Учебное пособие по матрицам ABCD Содержит пример системной матрицы всей системы.
ABCD Calculator Интерактивный калькулятор для решения матриц ABCD.

Энциклопедия физики

Получено с «http://en.wikipedia.org/»
Весь текст доступен на условиях лицензии GNU Free Documentation License

Домашняя страница

Формулировка матрицы в геометрической оптике — M Dash Foundation: C Cube Learning

Серия «Оптика», лекция — V

Это пятая часть лекция для выпускного класса по физике, прочитанная 3 февраля 2017 года.

(все лекции серии «Оптика») Прочесть другие доступные лекции серии 9 по оптике0038 Матричная формулировка в геометрической оптике : геометрическая оптика определяется пределом длины волны, который достаточно мал, чтобы путь световой волны можно было аппроксимировать прямыми линиями, называемыми лучами. С помощью этого приближения можно понять множество физических процессов, происходящих со светом, таких как отражение и преломление. При этом пределе возможна матричная формулировка оптических систем. Фото-кредит : mdashf.org

---

В этой лекции мы узнаем о

а. Матрица перевода

б. Матрица преломления

c. Системная матрица

В этой лекции мы обсудим один из самых интересных и мощных методов геометрической оптики . Как мы говорили в лекции — III, геометрическая оптика есть тот раздел оптики, в котором мы ограничены ситуацией, когда длина волны света пренебрежимо мала , т. е. незначительна по сравнению с размерами объектов, с которыми взаимодействует световая волна. .

Мы узнаем много подробностей о том, что такое световая волна, в следующих лекциях этой серии. Многие из них уже доступны на этом веб-сайте, например. смотрите вторую ссылку ниже.

(лекция — III) Подробнее о «геометрической оптике»

(Волны) Читайте о свете как волне

Как следствие, свет (волны) можно рассматривать как лучей или геометрические прямые линии и нюансы их свет, как волнообразные волны, можно отложить до счастливого часа.

Трассировка лучей

В пределе геометрической оптики любая общая оптическая система может быть связана с лучом, который можно проследить посредством двух основных типов прохождения луча: переноса и преломления . Таким образом, закон преломления  является центральным инструментом для трассировки лучей . Луч можно описать в оптической системе своими координатами . Вскоре мы определим координаты луча.

Наша цель — найти матрицу, управляющую смещение луча из одной координаты в другую координату при движении луча из одной геометрической точки в другую. Это позволит нам изучать как простые, так и гораздо более сложные системы наиболее эффективным и мощным способом, как мы увидим.

Давайте обсудим основные матрицы, доступные для трассировки лучей при переходе луча от одной координаты к другой в следующих двух случаях.

I. Матрица перевода

Матрица трансляции

актуальна, когда свет распространяется прямолинейным движением в однородной среде

II. Матрица преломления

Матрица преломления

относится к преломлению, возникающему на границе раздела двух разных сред

В общем случае чистая  прохождений луча может состоять из любого числа перемещений и любого числа  преломлений . Отражение было бы просто двумя переносами, а общее преломление можно сконструировать из преломления так же, как и из переноса, как мы увидим.

Таким образом, наиболее обобщенная оптическая система может иметь число переводов и числа преломления матрицы  так сказать, в соответствующем порядке. Полная или результирующая матрица будет называться системной матрицей .

I. Матрица переноса

Рассмотрим луч, пересекающий оптическую среду по прямой под любым углом. Это называется перемещением , поскольку единственное изменение, которому подвергается луч, — это перемещение или прямолинейное смещение координат. Излишне говорить, что это заставляет нас понять, что луч ограничен одним гомогенная среда .

Формулировка матрицы в геометрической оптике : Трансляция относится к трассировке лучей в одной однородной среде. Координаты луча преобразуются из одной точки (например, P) в другую точку (например, M или Q) посредством матричной формулировки оптической системы. Фото : mdashf.org

Обратите внимание, что на приведенной выше диаграмме мы показали две разные линзы, матрица переноса поможет нам только до точки Q. Нам потребуется дополнительная формулировка (матрица преломления), чтобы увидеть, что происходит. происходить внутри одного или нескольких объективов или любых других оптических носителей.

Луч был бы полностью охарактеризован, если бы мы могли указать необходимое количество координат луча, каким бы сложным он ни был. В нашем случае он простой, прямой. Поэтому нам нужно указать координаты любых двух точек, чтобы полностью указать наш луч.

В любой геометрической точке луча ее координата задается двумя переменными; высота от оси (показана на рисунке как PP’ для и MM’ для ) и угол от оси через  или (например, или ).

Мы определили наш луч в двух точках — следовательно, определили его полностью, задав две координаты (высота и угол — координаты луча ) — в двух разных геометрических точках (P и M — геометрические точки луча ): т. е. по координатам ( луча ) в геометрической точке P и по координатам ( луча ) в геометрической точке M . это на шаг ближе к определению оптических путей. Косинус оптического направления значительно упрощает жизнь, когда мы имеем дело с оптическими ситуациями. Если вам интересно посмотреть, как определяется оптический путь, перейдите по ссылке.

( Как определяется оптический путь? ) Нажмите, чтобы узнать больше об оптическом пути

Показатель преломления пригодится, даже если мы наслаждаемся простотой этой конкретной проблемы однородной среды. Эта новая переменная (косинус оптического направления) определяется как .

На нашем рисунке, показанном выше, луч движется прямолинейно в однородной среде , следовательно . Также . Если предположить наличие параксиальной области, это будет означать: . Это еще больше изменит уравнения, которые мы только что получили, на: Также имеем из этого: и .

(Что такое параксиальная область?) щелкните, чтобы увидеть, что означает параксиальная область

Опять же, поскольку наша среда однородна. Так как мы движемся прямолинейно то имеем: и .

Выражения в можно записать в терминах матриц: .

Таким образом, луч с координатой переходит в координату, и это движение представляется матрицей, известной как матрица переноса, где .

Фактическое расстояние, пройденное лучом в однородной среде, аппроксимируется и основано на наших параксиальное предположение . Мы тоже это видим.

II. Матрица преломления

Мы определили вид матрицы, которая будет отвечать за перевод луча из его начальной координаты в его конечную координату, если рассматриваемый луч проходит в одной однородной среде и следует прямой линии.

Более сложным процессом является преломление луча при встрече с границей раздела двух сред с разными показателями преломления. Анализируя прохождение луча, мы можем определить матрицу, которая управляет прохождением луча для преломления. Соответственно, мы называем это матрица преломления .

Давайте нарисуем подходящую диаграмму для этой ситуации. Мы будем рассматривать одну преломляющую поверхность и оставим без внимания дальнейшую конфигурацию поверхности. Таким образом, мы можем позже перейти к конфигурациям, которые могут иметь различную толщину и разные вторичные поверхности, после единственной поверхности слева, которая является сферической с радиусом кривизны .

Состав матрицы в геометрической оптике : Матрица преломления; матрица преломления относится к трассировке лучей в неоднородных средах. Координаты лучей преобразуются из одной точки в другую в неоднородных средах благодаря мощной матричной формулировке оптических систем. Фото : mdashf.org

Поскольку теперь луч пересекает две среды, преломляясь на границах сред, мы должны применить закон Снеллиуса , чтобы ограничить путь луча.

Кроме того, мы непреклонны в отношении параксиального прохождения луча, то есть луч держится как можно ближе к оптической оси, как по высоте, так и по углу, поэтому синус углов и т. д. будет аппроксимирован значением углов сам по себе, учитывая, что углы уже указаны в радианах последовательно.

а. закон Снеллиуса задается формулами  и b. параксиальное допущение определяется как .

Также мы запишем отношения между углами, как показано на приведенной выше диаграмме, чтобы мы могли выразить все в терминах наших ранее определенных координат луча, в терминах .

Итак, у нас есть где   — углы, образуемые падающим и преломленным лучами с осью z, то есть с оптической осью. Также   — это угол между нормалью (показанной как N) к преломляющей сферической поверхности с осью z.

— показатели преломления среды до преломляющей поверхности и среды после преломляющей поверхности соответственно.

Наше параксиальное предположение означает . Таким образом, мы имеем from ,  и используя we have: .

Если мы определим, у нас будет . называется силой преломляющей поверхности.

Теперь заметим, что высота луча в точке-P до и после преломления одинакова, поэтому: . вместе можно записать в виде матричного уравнения: . называется матрицей преломления, так что .

III. Матрица системы

В общем случае любая оптическая система состоит из серии преломляющих и поступательных движений луча. Таким образом, мы можем написать общую матрицу, которая преобразует координаты из одной точки конфигурации в другую при нашем параксиальном предположении.

где называется системной матрицей . Соответственно системная матрица является произведением любого числа возможных матриц преломления и трансляций . Это также легко увидеть, так как , и .

Отсюда следует, что элементы матрицы системы в общем случае удовлетворяют условию . безразмерны, имеют размерность обратной длины и имеют размерность длины.

Матрица в этой форме также называется матрицей ABCD из-за символов элементов, .

Оцените:

Mahisapat, Dhenkanal, Odisha 759001, India

Нравится:

Нравится Загрузка…

Rays: Casting and Paraaxial Optics

Optics Sampler

1. Параксиальная геометрическая оптика и системная матрица

Математические модели

«А теперь рассмотрим сферическую курицу…»

— седая изюминка

Этот материал из первых четырех (из 25) Главы в [2], типичном учебнике для второкурсников.

Свет — это электромагнитная волна со многими удивительными свойствами. Нравится также будучи элементарной частицей. Так много для глав 1 и 2 из [2].

Преломление — это отклонение света оптической средой; отражение это отражение света от поверхности. В геометрической оптике ([2], гл.3) рассматривается частный случай физического оптика которая бросает за бортом все волновые (и вообще квантовые) свойства света. Христиан Гюйгенс (голландец, 1629 г.р.) разработал теорию света, основанную на эфире. это было своего рода геометрическое оптическое приближение в том смысле, что оно не для дифракции, но вывел закон преломления. Пьер Ферма (Французский, б. 1601) использовал аргумент принципа минимума (минимизация пути света время) для доказательства того же закона. Его принцип также не совсем верен, так как там оказываются максимизирующими время световыми путями и случаями, когда все пути находятся эквивалентны во времени (например, между фокусами эллипсоидального зеркала).

Закон преломления не зря называется Закон Снелла. Во-первых, его звали не Снелл, а Виллеброрд. Снеллиус (Голландский, р. 1580). Для другого закон известен давно, Вы можете поспорить с первым предком человека, чье копье перешел рыбу знал об этом. Некий Ибн Сахл (Персия, около 940 г. н.э.) открыл его. (его рукопись находится на обложке этой страницы проекта.) Его исследовали Птолемей (греч., около 90 г. н. э.) и Витело в средние века, но у них не было формализма, чтобы записать это, и вместо этого используются таблицы. Так что же это такое?

Закон преломления (закон Снелла): Когда луч света преломляясь на границе двух однородных сред, прошедший луч остается в плоскости падения, а синус угла преломление прямо пропорционально синусу угла заболеваемость.

Есть еще закон отражения : Когда луч света отраженный на границе раздела двух однородных сред, отраженный луч остается в плоскости падения, а угол отражения равен углу падения. Плоскость падения определяется падающий луч и вектор нормали к поверхности в точке падения.

Закон Снелла обычно записывается так:
n ₁ sin θ ₁ = п ₂ sin θ ₂ ,
с n ₁ , n ₁ преломление индексы двух сред, где скорость света v в среде показателя преломления n равно v = c/n , если c равно скорость света в вакууме. Более низкая скорость света в вторая среда, большее преломление. Вот картина отражения и преломления.

Теперь, используя эти два закона, мы можем анализировать системы линз и зеркал. как система со всеми объективами ниже:

После всего этого мы хотели бы использовать закон Снелла в нашем приближении геометрической оптики. к реальности. Но у нас есть проблема. Эти синусы нелинейны функции. Мы не сможем найти решения простыми линейными методами мы знаем и любим. Ну тогда! Давайте добавим еще немного реальности в мусорное ведро Давайте просто рассмотрим только параксиальный лучи, те, что никогда делать большие углы с оптической осью. На самом деле, те, для которых мы можем приблизительно,
с углами, измеряемыми в радианах, а не в градусах (!!) ,
sinθ = tan θ = θ .
Это проясняет ситуацию: теперь параксиальный закон Снеллиуса равен
n ₁ θ ₁ = n ₂ θ ₂ .

Параксиальное предположение является примером «малого угла приближение», столь дорогое для физики и техники. линейное приближение , описывающее заданную функцию (в некоторой местности) как линейная функция. Вот, например, sin(x) ≅ x около 0. В будущем вы часто будете расширять функции в бесконечный ряд (Тейлора) и игнорировать все, кроме первого члена, чтобы получить линеаризация. Получается, что sin(x) = x — x ³ /3! + х ⁵ /5! — … , около 0, а для маленьких x мы рассматриваем только первый срок.

Теперь обратите внимание на рисунок выше, что разные лучи будут проходить разные расстояния через линзы, которые толще и тоньше. Так только то, что происходит, зависит только от того, где и под каким углом луч входит Объектив. Ну неудобно. Но ждать! Мы знаем, что делать! Просто отбросьте этот кусочек реальности. тонкая линза предположение: «рассмотрите бесконечно тонкую линзу» со всеми преломляющий мощность и ни один из раздражающих размеров реального объекта. Диаграмма может выглядеть так, с X для выпуклых и V для вогнутых линз:

Используя довольно простую алгебру (но довольно сложные диаграммы) [2] выводит элегантные формулы для полезных, практичных чисел, которые помощь в понимании и создании линз. Они получены из базовая геометрия (скажем, радиусы кривизны, расстояние) и базовая физика (закон Снеллиуса, показатели преломления). Результатом являются используемые параметры, описывающие сферические зеркала. преломление на сферических поверхностях, тонких линзах и т. д.

Важной концепцией тонкой линзы является ее фокусное расстояние f , т.е. (со знаком) расстояние до изображения объекта на бесконечности. Выпуклые линзы имеют положительные фокусные расстояния, вогнутые отрицательные). Уравнение производителя линз предсказывает фокусное расстояние линзы. с точки зрения его показателя преломления, среды, в которой он находится, и его радиусы кривизны. В воздухе (с показателем преломления n = 1 ), одна версия уравнения тонкой линзы утверждает, что объект в расстояние s отображается в точке s’ линзой с фокусным расстоянием ф если 1/с + 1/с’ = 1/f . Мощность P объектива измеряет насколько сильно он преломляет свет, и определяется как 1/ф . В плоскости х-у, Измеряем углы (в радианах), на которые лучи отклоняются от оптической системы ( x ) ось (лучи, параллельные оси абсцисс, равны 0 радианам). Лучи слева, восходящие в направлении y , положительны. Линза преломляет падающий луч под углом θ , согласно наши приближения, чтобы придать ему новый угол:
θ’ = θ — yP
если луч падает на линзу на высоте y . Таким образом
θ’ = θ -(1/f)y

Это наш краткий обзор [2], гл. 3. Помните об углах всегда в радианах, а не в градусах. Итак, теперь мы можем использовать нашу параксиальную геометрическую оптическую сферическую курицу. и сделать некоторые (приблизительные) рассуждения. Ебать в сторону, создавая разрешимый линейные приближения — важнейший навык, который вы будете развивать в следующий три года.

Метод

Часто линейные системы описываются комбинацией (суммирование, умножение, свертка,… или другие линейные операторы) преобразования, производимые частями системы. Мы опишем луч, движущийся слева направо на его мгновенную высоту и угол полета: [y,θ] ^T . мы увидим это параксиальные оптические элементы может быть описана матричными преобразованиями 2×2 ( переносов лучей функции ) представляющий что случается с лучом на оптическом элементе, а произведение передаточные матрицы описывают оптическую систему как передача системы функция . Этот материал освещен в [2] гл. 4, например.

Изобразите систему, как указано выше, двухмерный график зависимости Y от X с осью X. является оптической осью. Отображаемый объект считается находящимся на входной плоскости в в слева от диаграммы (ниже x = 0 ), а выход самолет везде, где мы хотим вычислить окончательную высоту луча. Вещи мы возможно, вы захотите узнать о включении системы (есть еще много других) это спереди и сзади фокусное расстояние . Последний как раз тот эффективное фокусное расстояние всей системы, а первое равно аналогично точка фокусировки лучей под углом 0, идущих справа и направленных влево. осевая точка изображения точки объекта, находящейся ближе бесконечности на оптическая ось находится там, где на оптической оси фокусируются все его лучи (да, все они проходят через одну точку). Плоскость изображения — это плоскость (линия на двумерной диаграмме) через осевую точку изображения, перпендикулярную в оптическая ось.

линейное увеличение системы y _f /y ₀ , относительная высота луча в входная и выходная плоскости.

Рассмотрим луч [y ₀ , θ ₀ ] ^T движущиеся (транслирующиеся) через однородную среду. Углы измеряется в радианах, помните. Если он перемещается в осевом направлении на L под углом θ ₀ , Его новое описание:
[y ₀ + L тангенс θ ₀ , θ ₀ ] ^T . Параксиальное предположение состоит в том, что tan(x) = sin(x) = x , поэтому мы можем описать результирующий линейный преобразование описания луча по

|у  1  | = |1 л| |у  0  |
|θ  1  | = |0 1| |θ  0  |
 

Эта простая матрица — то, как мы описываем изменение луча, как если бы движется через некоторую однородную среду на осевое расстояние.

Помните это уравнение в конце предыдущего раздела?
θ’ = θ -(1/f)y .
Угадайте, что для тонкой линзы?

|у  1  | = |1   0| |у  0  |
|θ  1  | = |-1/f 1| |θ  0  |
 

С учетом работы в [2] гл. 3 тоже легко придумать простой передаточные матрицы для сферических или преломляющих интерфейсов, сферические зеркала и толстые линзы. Мы не будем их использовать, но они простые.

Выразите параксиальную систему с элементами, описанными матрицами 2×2, скажем М1, М2, М3, М4 в порядке слева направо. Тогда для луча р , M1 *r — луч после первого элемента, М2*М1* р , М3*М2*М1* р и M4*M3*M2*M1 — полное преобразование и матрица передачи системы.

Этот метод переноса лучей используется для нахождения других основных геометрических характеристики описывающая оптическую систему, например, ее узловые точки, а также первую и вторую главные плоскости. Не только это, но и четыре элемента матрицы передачи имеют различимую семантику, которую можно осветить, рассмотрев в физический смысл установки каждого из них в ноль. На данный момент, однако, мы закончили.

Примеры

Найдем несколько важных расстояний для примера оптической системы. Рассмотрим три линзы с фокусным расстоянием 200, -50 и 50 мм. Первый и второй разделены на 100 мм. второй и третий на 50 мм. входная плоскость 200 мм. перед первой линзой. Что такое (спина, эффективное) фокусное расстояние системы?

Направляем луч параллельно оси в 6-элементную систему (перевод, объектив, перевод, объектив, перевод, объектив). Последний луч, который мы получаем, исходит из последней линзы на X = 350. оказывается быть (3, -.04) ^Т . Мы после фокусного расстояния g= y/tan(θ) , (основание последнего треугольника в цифра от X= 350 до X= 425). В предположении малого угла тангенс угла есть угол, поэтому этот луч пересекает ось в точке г = y/θ или 75 мм. Затем мы можем добавить последний, седьмой, перенос этого расстояния, который должен привести луч вниз к оси в фокусе, и эта конечная система произвела рисунок выше.

Осевая точка изображения системы находится там, где изображение луча начинаясь в начале координат, пересекает оптическую ось. Это как фокальной точки, и рассчитывается таким же образом, только с использованием другого начальный луч. Получается, что все изображения системы указывают на объект в начале координат упадет в плоскости на этом расстоянии, поэтому именно здесь будет сформировано сфокусированное изображение.

Ради интереса давайте воспользуемся немного другой системой с тремя линзами: линзы разнесены на 300, 100 и 50 фокусных расстояний 200, -50 и 50. Проведение луча из начала координат под углом 0,01 и вычисление осевое расстояние изображения (это 95 мм от третьей линзы), мы можем составить окончательный перевод после 3-й линзы 95 мм, чтобы получить этот график:

По этой же системе пускаем три луча из какого-то ненулевого y под тремя разными углами: они должны пересекаться в той же осевой плоскости изображения, что и выше. Хорошо, все лучи из одного и того же точка объекта оказывается в одной точке изображения (совпадение?!) и мы можем использовать высоту y в плоскость изображения, чтобы получить соотношение высоты объекта/высоты изображения, или же линейный увеличение, как 0,2 (высота изображения перевернута).

2. Raycasting и системы линейных уравнений

Проблема и метод

Raycasting — это основная операция при рендеринге компьютерной графики. представления в образы. Идея звучит просто: дано очко зрения и направление взгляда (луч), вычислить цвет и интенсивность свет в этом направлении. В геометрическая оптика волна природа света игнорируется, и следовать световым путям (лучам) через оптических систем нам нужна только геометрия, немного алгебры и несколько физические законы.

Базовый случай: дана трехмерная точка начала луча и его направление, где оно пересекает данную плоскость в пространстве? Нет отличается от задачи «прямая-плоскость пересечения», а в оптике иногда называется «пересечением луча с плоским зеркалом», потому что зеркала наиболее распространено использование оптических «квартир».

Как обычно, представьте точки p, x, r и т. д. в 3D с помощью (x,y,z) ^T векторов. Представим направления α, β и т. д. в 3D по (x, y, z) ^T единичных векторов. Они образуют семью, которая живет на сфере единичного радиуса с центром в источник. Вы можете видеть, что каждому направлению соответствует вектор (точка) чья голова находится на этой гауссовой сфере .

Стандартный способ пересечения вектора с поверхностью в пространстве — растянуть вектор наружу в его направлении до пересечения с поверхностью. Полученная длина это все, что нам нужно, так как мы можем тогда вычислить точку пересечения.
Итак: Любую точку на луче можно записать
Луч: r = r ₀ + d α ,
с d длина, r ₀ начало луча, α это направление. Это векторное уравнение представляет три линейных уравнения в x,y,z .

Уравнение плоскости является линейным, и трехмерная версия знакомой линии уравнение:
Плоскость: Ax + By + Cz + D = 0
Записанный так, [A, B, C] ^T — это вектор, определяющий направление, на самом деле направление нормали к плоскости. Масштабирование всего уравнения так что это направление является единичным вектором, дает новое масштабированное значение Д значение: это перпендикулярное расстояние от плоскости до источник. Мы сразу же упростим себе жизнь, заставив бесконечное зеркало или плоскость, чтобы пройти через начало координат, чтобы мы могли опишите его линейным уравнением: одно строго через (x,y,z) ( Д = 0 : нет неприятная постоянная).
Плоскость через начало координат: Ax + By + Cz = 0 или
(A/C)x + (B/C)y + z = 0 .

В сторону: Реальное литье на самом деле хочет быть описанным с проективная геометрия , увлекательная а также красивая ветвь математики. Камера (обскура) проецирует сцену на сенсор с помощью рейкастинга, и мы получаем знакомую перспективу такие эффекты, как параллельные железнодорожные пути, которые, кажется, сходятся воедино. на расстоянии. Это не -линейное преобразование: линейное преобразования сохраняют параллелизм. К счастью, есть хитрый трюк для выполнения необходимых вычислений линейно (строго матрично операции) только в простой четырехмерной версии пространства ( однородный координаты ). Для более общего проекта рейкастинга все еще довольно легкий, видеть Пинхолы и пляжные мячи. Этот проект визуализирует сферы, так как бесконечный плоскости скучны, а небесконечные плоские поверхности очень неудобны.

Уравнения Ray и Plane выше представляют собой четыре линейных уравнения. А их решение дает d , в котором луч пересекает самолет, и мы закончили. Превью: пишем уравнения, делаем быстро массаж, запишите их в матричной форме и ответ очевиден.

Начало луча: (x ₀ , y ₀ , z ₀ ).
Направление луча: (α ₁ ,α ₂ ,α ₃ ).
3 уравнения луча, 1 уравнение плоскости:
х = х ₀ + α ₁ д
у = у ₀ + α ₂ д
z = z ₀ + α ₃ d
(А/С)х + (В/С)у + z = 0 .

Нам нужно четыре уравнения для неизвестных x,y,z,d , но явно мы Только действительно нужно три числа, x,y,d скажем, из которых мы можем легко найдите z , используя уравнение плоскости через начало координат. Превентивное использование сначала это уравнение, мы получаем выражение для z , чтобы заменить в уравнение третьего луча, и мы можем переписать систему как:
x ₀ = x — α ₁ d
у ₀ = у — α ₂ д
з ₀ = -(A/C)x — (B/C)y — α ₃ d .

Мы могли бы продолжить подстановку, чтобы решить систему, но давайте представим это как матричное уравнение:
[х ₀ , у ₀ , г ₀ ] ^Т = М [х, у, д] ^Т , где М
| 1 &nbsp &nbsp &nbsp &nbsp &nbsp &nbsp 0 &nbsp -α ₁ |
| 0 &nbsp &nbsp &nbsp &nbsp &nbsp &nbsp 1 &nbsp -α ₂ |
| -(А/С) -(В/С) α ₃ |
.

No related posts.