Учимся ездить на механике правильно ч.1 — теория | Двигун
Переключатель МКПППереключатель МКПП
Учимся ездить на механике правильно ч.2 — практика
Как ездить на механике? Если вы задаете себе такой вопрос, то данная статья поможет вам во всем разобраться. Для начала, очевидно, что «водить на механике» предполагает вождение автомобиля с механической коробкой передач. Поскольку многие водители ездят только на автомобилях с автоматическими коробками передач, это может показаться поначалу немного пугающим и странным. Во время вождения на МКПП, необходимо активно переключать передачи с помощью сцепления и переключателя передач (также называемого рычагом). То есть водителю необходимо понимать, когда следует переключать передачи от 1 до 5, на какую передачу нужно переключиться и когда необходимо отпустить сцепление. Однако, как и в любом другом деле, вам просто необходимо немного попрактиковаться.
Практика вождения на механической коробке поможет вам стать настоящим профессионалом в данном деле! Здесь просто необходимо немного терпения. Отлично, если у вас есть человек или наставник, который уже умеет управлять автомобилем на МКПП и сможет вас научить практике вождения на механической коробке передач на дороге. Естественно, что помимо теории есть еще и практика, которая является наиболее важной. Вождение на МКПП требует от водителя определенного чувства / внимания к тахометру, того момента, когда необходимо переключить передачу. Таким образом, практический опыт имеет первостепенное значение.
Несмотря на то, что на сегодняшний день большинство автомобилей имеют автоматическую коробку передач, навык управления автомобилем с механической коробкой передач поможет вам в будущем легко управлять любым автомобилем. Как только вы освоите вождение на МКПП, вам покажется странным, что езда на механике когда-то вызывала сложности. Здесь просто нужна мышечная память, и хотя процесс обучения немного кропотливый вначале, когда вы немного попрактикуетесь, вам даже понравится водить автомобиль на МКПП. Для начала давайте взглянем на тех. часть вождения и что же творится «под капотом» когда мы переключаем передачи.
Итак, как работает переключение передач?
Для начала, шестерня (зубчатое колесо) в автомобиле «переключает» мощность с коленчатого вала (ось, которая вращается и принимает мощность от вашего двигателя) на карданный вал. Механизмы работают в диапазоне низких передач (1 и 2), средней передачи (3) и высоких передач (4 и 5). Как правило, вы увеличиваете передачу по мере увеличения скорости езды. Таким образом, более высокая скорость соответствует более высокой передаче. Некоторые легковые автомобили могут иметь 6 передач, но 5 — это норма + задняя передача.
До того, как вы научитесь переключать передачи, важно знать, какие педали вы будете использовать. Они делятся на следующие виды:
Сцепление
Педаль сцепления находится слева. Её необходимо использовать для эффективного переключения передач. Задача сцепления – непродолжительное отключение двигателя от ведущих колес автомобиля, а также плавное последующее соединение работающего мотора с ведущими колесами. После этого вы можете быстро и легко переключать передачи. Необходимо помнить, что прежде, чем переключать передачи, вы всегда нажимаете на педаль сцепления до упора!
После этого вы можете быстро и легко переключать передачи. Необходимо помнить, что прежде, чем переключать передачи, вы всегда нажимаете на педаль сцепления до упора!
Таким образом, ваше сцепление всегда будет зажато левой ногой. То есть сначала необходимо зажать сцепление, прежде чем переключить передачу и переместить рычаг переключения передач в правильное положение.
Если вы привыкли к вождению авто на автоматической коробке передач, и никогда не задействовали левую ногу, то поначалу данный процесс покажется вам странным. Однако, немного потренировавшись, вы привыкнете задействовать эту ногу и процесс станет более естественным для вас.
Тормоз
Тормоз расположен посередине. Тут все банально и просто. Тормоз нужен для того чтобы остановить автомобиль. Вообще, остановить авто на МКПП можно 3 способами!
- Если нужно просто остановиться, то классически скидываем передачу на нейтралку с передачи и нажимаем тормоз;
- Если остановка должна быть аварийной, т.
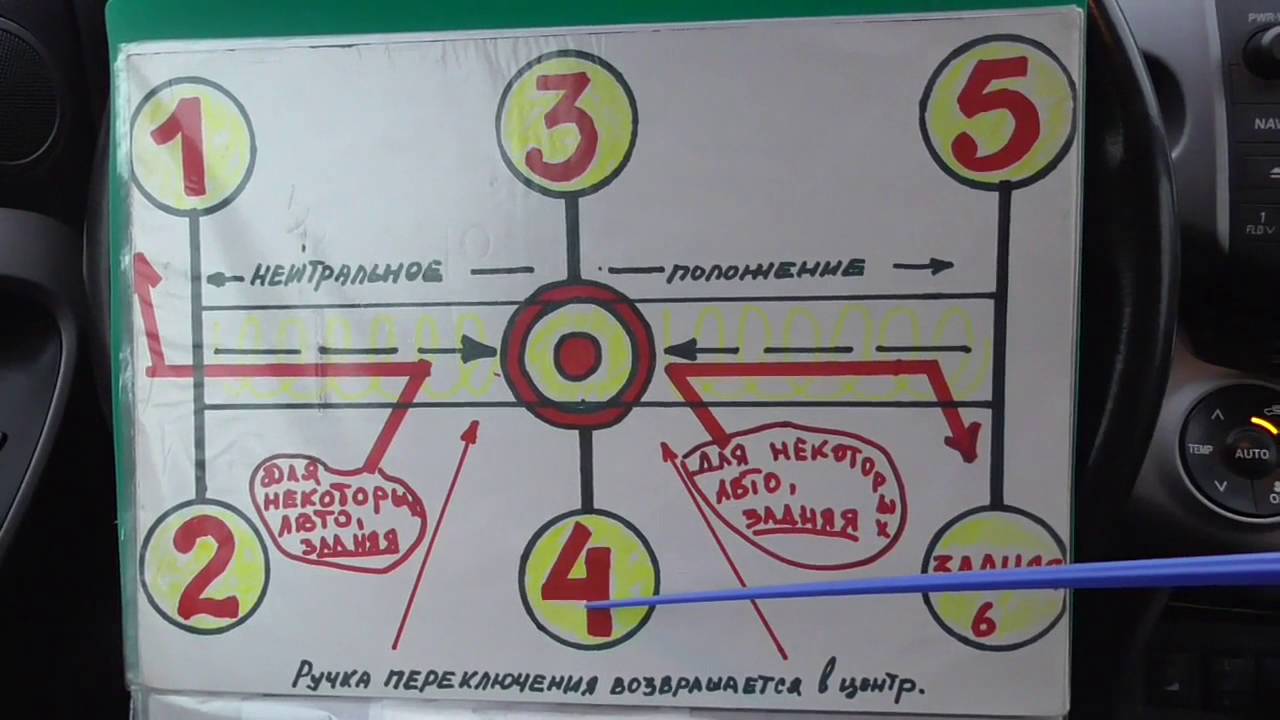 е внезапное торможение, то можете смело жать просто на педаль тормоза без выключения передачи;
е внезапное торможение, то можете смело жать просто на педаль тормоза без выключения передачи; - Торможение двигателем — полезна в зимнее время года, но об этом типе торможения далее в статье.
Акселератор
Акселератор (педаль газа) заставляет вашу машину двигаться быстрее. Он расположен правее тормоза. По мере увеличения скорости движения авто, вам естественно захочется увеличить скорость.
Таким образом, переключаем скорость по мере увеличения скорости езды (более высокие передачи для более высоких скоростей), и понижаем скорость по мере замедления езды (более низкие передачи для более медленных скоростей!)
Просто запомните последовательность этих педалей как В Б А (то есть привычная нам последовательность А Б В только задом наперед). Сцепление, Тормоз, Газ.
В следующей части я подробно распишу всю практическую часть и нюансы управления авто на МКПП.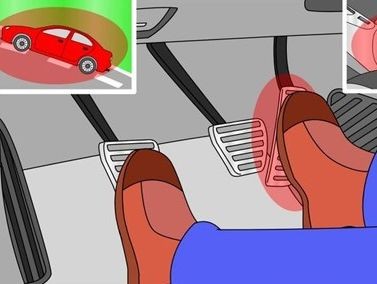 Поэтому настоятельно рекомендую вам перейти к практической части, чтобы сформировать полную картину управления авто на МКПП.
Поэтому настоятельно рекомендую вам перейти к практической части, чтобы сформировать полную картину управления авто на МКПП.
Огромное спасибо за прочтение моей статьи!
Пожалуйста, подпишитесь на мой канал и просто поставьте лайк этому посту.
Буду также благодарен за любой репост в соц. сети 🙂
Написание качественных статей очень большой труд и я рассчитываю на вашу поддержку.
Секреты езды на механике в городе. Как ездить на механике для чайников: рекомендации
Прежде чем сесть за руль любого автомобиля, необходимо изучить правила дорожного движения, а также технические и функциональные характеристики транспортного средства, общее устройства автомобиля и т.п.
При этом хотя автомобиль может быть оснащен или , на практике начинающий автомобилист не всегда сам выбирает коробку переключения передач, которой буде оборудован учебный авто.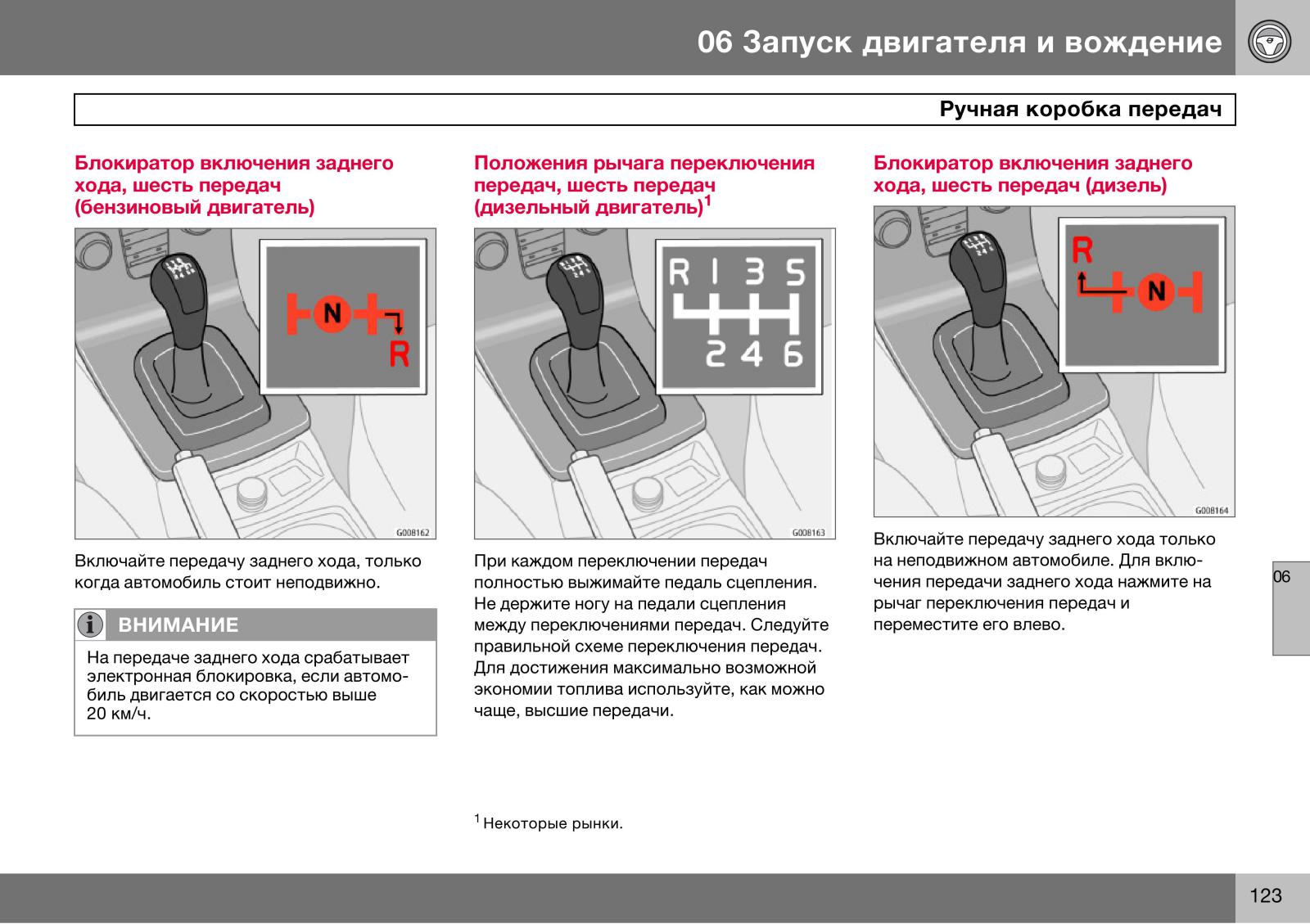 В данной статье мы поговорим о том, как научиться правильно водить машину на механике с нуля.
В данной статье мы поговорим о том, как научиться правильно водить машину на механике с нуля.
Читайте в этой статье
Учимся водить машину с механической коробкой передач
После того, как была произведена подготовка водительского места (настроено водительское сидение, боковые зеркала и зеркало заднего вида), можно приступать к ознакомлению с педальным узлом.
Автомобиль на механике оснащен тремя педалями: , тормоз и акселератор (газ). Педаль сцепления расположена слева, педаль тормоза посередине, а педаль акселератора справа.
- Педаль сцепления предназначена для передачи крутящего момента и плавного переключения передач. Причем переключать передачи можно только при выжатой педали сцепления.
Водитель выжимает педаль сцепления быстрым нажатием, отпускает плавно, учитывая свободный ход сцепления до момента контакта диска сцепления с маховиком двигателя и начала движения транспортного средства. После того как автомобиль тронулся с места, необходимо дозированно нажать педаль акселератора и убрать ногу с педали сцепления.
- Педаль тормоза нажимается правой ногой и служит для торможения автомобиля. Усилие нажатия на педаль тормоза, в первую очередь, зависит от скорости движения и дорожных условий. Чем меньше скорость – тем меньше усилие.
- Педаль акселератора. Посредством педали акселератора водитель изменяет количество топливной смеси, попадающей в , тем самым увеличивая или уменьшая скорость вращения коленчатого вала.
Соответственно, изменяется скорость движения автомобиля. Чем сильнее водитель давит на педаль акселератора, тем больше топливной смеси поступает в цилиндры двигателя, увеличиваются мощностные показатели ДВС.
Начинающий водитель должен запомнить, что при управлении автомобилем, оборудованным МКПП, правая нога переносится с педали газа на педаль тормоза и наоборот, а левая работает только с педалью сцепления. Исключением является применение спортивных техник управления, когда торможение может быть выполнено профессионалом левой ногой.
- Рычаг переключения передач предназначен для изменения передач МКПП при движении автомобиля.
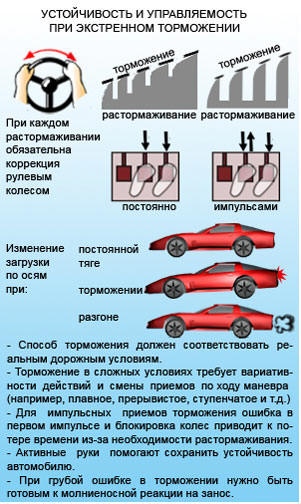 Каждая ступень МКПП соответствует определенному скоростному режиму. При увеличении скоростного режима водителю необходимо включать повышающую передачу, а при снижении скорости, соответственно, включать понижающую передачу.
Каждая ступень МКПП соответствует определенному скоростному режиму. При увеличении скоростного режима водителю необходимо включать повышающую передачу, а при снижении скорости, соответственно, включать понижающую передачу.
Как водить машину на механике: пошаговая инструкция
- Занимаем правильное положение за рулем автомобиля, проверяем положение рычага (должен быть переведен в нейтраль).
- Поворачиваем ключ в замке зажигания и заводим двигатель автомобиля.
- Далее правой нажимаем на тормоз, левой ногой выжимаем педаль сцепления и включаем первую передачу.
- Затем отпускаем тормоз, переносим правую ногу на газ и одновременно плавно отпускаем педаль сцепления.
- После того, как автомобиль слегка тронется, дозируем тягу педалью акселератора до момента начала уверенного движения автомобиля.
- После начала движения автомобиля полностью убираем ногу с педали сцепления и продолжаем нажимать на педаль акселератора с цель последующего набора скорости автомобиля.

- При достижении необходимого скоростного режима, рекомендованного для движения автомобиля на первой передаче, отпускаем газ, снова выжимаем сцепление и включаем вторую передачу. При этом сцепление уже можно отпустить немного резче, чем при старте на первой.
- При правильном выборе нужной передачи коробка будет переключаться без толчков и рывков.
- первая передача 0-20 километров в час;
- вторая передача 20-40 километров в час;
- третья передача 40-60 километров в час;
- четвёртая передача 60-90 километров в час;
- пятая передача 90-110 километров в час;
- шестая передача свыше 110 километров в час.
Вождение машины с механической коробкой передач: торможение
При плавном торможении или притормаживании водитель должен перевести правую ногу с педали газа на педаль тормоза, добиваясь снижения скорости автомобиля до необходимого уровня.
После чего, если нет необходимости полной остановки автомобиля, водитель должен выжать сцепление, включить передачу, соответствующему данному скоростному режиму и продолжить движение.
В случае экстренного торможения водитель должен убрать ногу с педали акселератора, перенести ее на педаль тормоза и нажать на тормоз до полной остановки автомобиля. Если ситуация позволяет, одновременно вместе с тормозом выжимается и педаль сцепления, а рычаг переключения передач переводится в нейтраль.
Как водить машину на механике во время движение задним ходом
Прежде всего, нужно убедиться по зеркалам заднего вида в отсутствии преград за автомобилем. Поворачивая голову, убеждаемся в отсутствии преград для движения автомобиля задним ходом в «мертвых зонах» (это «слепые» зоны сзади и сбоку от автомобиля, которые не просматриваются в зеркалах заднего вида.)
Далее выжимаем педаль сцепления, включаем заднюю скорость и подгазовывая, плавно отпускаем педаль сцепления (аналогично первой передаче). При этом важно помнить, что задняя передача самая «тяговитая», а также включать заднюю передачу можно только после полной остановки автомобиля.
При начале движения автомобиля задним ходом педаль сцепления не следует сразу полностью отпускать, а также нужно очень аккуратно и плавно дозировать тягу педалью акселератора, дабы не допустить резкого рывка авто и потери управления автомобилем.
Двигаясь задним ходом, следует не совершать резких поворотов рулевого колеса или крутить руль рывками, поскольку это также может привести к потере контроля над транспортным средством и ДТП.
После преодоления задним ходом необходимого участка дороги, нужно убрать ногу с педали акселератора, выжать сцепление и нажать на педаль тормоза, полностью останавливая транспортное средство. Одновременно с педалью тормоза после нажатия на педаль сцепления рычаг МКПП переводится в нейтральное положение.
- Если необходимо припарковать автомобиль, тогда убеждаемся, что данное транспортное средство не создает преград для движения другим транспортным средствам. Также парковка должна выполняться с соблюдением ПДД.
После остановки ТС удерживаем нажатой педаль тормоза и сцепления, проверяем положение рычага МКПП (рычаг должен быть в положении нейтраль), затягиваем ручной тормоз, убираем левую ногу с педали сцепления, отпускаем тормоз и глушим двигатель.
Читайте также
Правильное переключение передач на автомобиле с механической коробкой: когда включать ту или иную передачу на МКПП, работа с педалью сцепления, ошибки.
Впервые сел за руль автомобиля с механической трансмиссией и не знаешь, как вообще начать движение? Не умеешь вовремя переключать скорости на механике? Ответы на все эти, а также другие вопросы, которые очень часто интересуют начинающих водителей, вы сможет найти в нашей сегодняшней статье.
Почему нужно уметь водить машину на механике
Вы никогда не знаете, в какую ситуацию попадёте в ближайшее время. Возможно, вам придётся одолжить чужой автомобиль, который будет оснащен механической коробкой передач. Или ваш друг захочет выпить, и обратится к вам с просьбой доставить его домой на его же авто с МКПП? А что с прокатом автомобилей за рубежом? Машины на механике встречаются намного чаще, нежели авто с АКПП.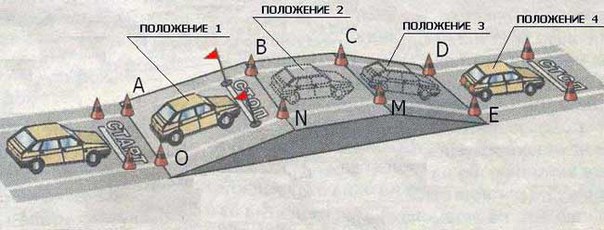
Если вы научитесь ездить на механике, вас ничто не застанет врасплох. Человек, который понимает, как ездить на автомобиле с механической трансмиссией, с легкостью сядет за руль машины с «автоматом», но не наоборот.
Машины с ручной трансмиссией, в большинстве случаев, стоят меньше, чем аналогичные версии с АКПП. Вы сэкономите деньги не лишь при покупке автомобиля. Вождение на механике – это серьезная экономия средств в течение многих лет эксплуатации транспортного средства, поскольку расход топлива таких автомобилей очень часто является меньшим, по сравнению с автоматическими трансмиссиями. Поскольку цены на топливо неумолимо растут, выгода будет очевидной.
Если аккумулятор вашего автомобиля с МКПП разрядился, вы сможете начать движение. Один из вариантов – воспользоваться проводами для прикуривания. Если их под рукой не оказалось, всегда можно завести машину “с толкача”. Забудьте об этой идее, если вы используете автомобиль с автоматической трансмиссией.
Многие спорткары доступны исключительно с механической трансмиссией. В особенности это касается многих моделей, выпущенных несколько десятков лет назад. В большинстве случаев производители таких машин понимают, что получить истинное удовольствие от вождения мощного авто можно лишь с механической КПП.
Водить машину на механике гораздо веселее! Если вы всю жизнь проездите на АКПП, вы так и не узнаете, что такое настоящий контроль над автомобилем. Езда на машине с «автоматом» очень искусственная и пассивная. А вот механика позволяет вам стать с автомобилем одним целым.
Как правильно ездить на механике: основы
Первое: познакомиться с местом водителя
Педали: сцепление, тормоз, газ. Педаль сцепления расположена слева, её нет на автомобилях с автоматической коробкой передач. Её надо нажимать при переключении передач вверх или вниз. Больше информации будет далее.
Педаль тормоза расположена по центру. Как вы, наверное, понимаете, она создана для торможения.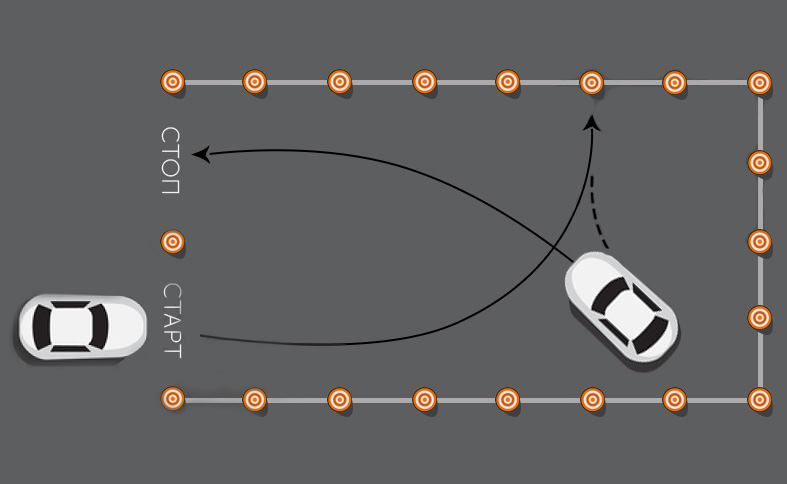
Крайняя правая педаль – это газ. Функционирует по тому же принципу, что и педаль газа в машине с АКПП.
Людям, которые впервые садятся в автомобиль с механической коробкой, трудно привыкнуть к тому, что теперь надо пользоваться ещё и левой ногой. Ведь в машинах с «автоматом» задействована лишь правая нога. Левая нога будет нажимать педаль сцепления, а правая нога – отвечать за тормоз и газ.
Рычаг переключения коробки передач. Именно с помощью него будем переключать передачи, он смещает шестерни в трансмиссии автомобиля. Многие новые автомобили с ручной коробкой оснащаются шестью передачами. Как правило, на ручке переключения КПП имеется подсказка, с помощью которой вы сможете понять, какие позиции рычага отвечают за определенную передачу. Это поможет вам правильно водить машину на механике.
Тахометр. Это один из элементов приборной панели автомобиля, который отображает количество оборотов в минуту коленвала двигателя. Когда вы только начинаете водить автомобиль с механической коробкой передач, тахометр поможет вам определить, когда именно надо переключаться вверх или вниз. В большинстве случаев необходимо включать более высокую передачу, когда стрелка тахометра достигает “3” или 3000 об./мин. Если же она опускается до отметки “1” или 1000 об./мин, необходимо переключаться вниз. После получения некоторого опыта вождения на механике вы сможете с легкостью определить, когда именно надо переключаться, реагируя на звук работы мотора. Больше об этом читайте ниже.
В большинстве случаев необходимо включать более высокую передачу, когда стрелка тахометра достигает “3” или 3000 об./мин. Если же она опускается до отметки “1” или 1000 об./мин, необходимо переключаться вниз. После получения некоторого опыта вождения на механике вы сможете с легкостью определить, когда именно надо переключаться, реагируя на звук работы мотора. Больше об этом читайте ниже.
Переключение скоростей и нажатие педалей сцепления и газа на выключенном двигателе
Перед тем как начать применять дальнейшие советы на практике советуем потренироваться делать всё с выключенным двигателем и включенным стояночным тормозом. Это поможет вам почувствовать зацепление и расцепление шестерней трансмиссии. Также вы сможете научиться плавно нажимать педаль сцепления.
Как тронуться с места на автомобиле с МКПП
Вероятно, самая пугающая часть процесса обучения вождению машины на механике – это начало движения на первой передаче. Вам понадобится некоторое время, чтобы понять, как лучше отпускать сцепление и нажимать на газ, чтобы поймать тот самый оптимальный момент и начать движение.
Практиковаться лучше на пустой стоянке. Покрытие должно быть ровным, наличие каких-либо иных транспортных средств поблизости крайне нежелательно. Желательно, чтобы на переднем пассажирском кресле находился человек, который четко понимает и умеет правильно ездить на механике.
Нажмите на педали сцепления и тормоза, после чего запустите двигатель. Чтобы завести автомобиль с механической коробкой всегда нажимайте сцепление ещё до того как будете включать зажигание. Хотя держать правую ногу на педали тормоза при запуске мотора в машине на механике необязательно (как это делают в автомобилях с автоматической трансмиссией), эта привычка вам не помешает.
Левая нога полностью выжимает педаль сцепления, а правая нога нажимает на тормоз. Заводим машину.
Включение 1-й передачи. Переводим рычаг переключения КПП в положение, соответствующее первой передачи.
Ни в коем случае не переключайте передачи до тех пор, пока педаль сцепления не выжата полностью!
Если вы не будете придерживаться этого простого правила, то услышите очень неприятный скрежет. Если ситуация будет повторяться неоднократно, вам придётся ехать к автомобильному мастеру. Убедитесь в том, что ваша левая нога, по-прежнему, выжала педаль сцепления до упора, после чего включайте 1-ю передачу.
Если ситуация будет повторяться неоднократно, вам придётся ехать к автомобильному мастеру. Убедитесь в том, что ваша левая нога, по-прежнему, выжала педаль сцепления до упора, после чего включайте 1-ю передачу.
Для этого надо использовать правую руку и переместить рычаг переключения передач вверх и влево.
Убедитесь в том, что передача действительно включена. Это можно легко почувствовать, а также увидеть. Рычаг должен оставаться на месте после того, как вы уберёте от него руку.
Держите ноги на педалях сцепления и тормоза, полностью выжав их. Не снимайте левую ногу с педали, в противном случае автомобиль заглохнет. Переместите правую ногу с педали тормоза на педаль газа. Приблизительно в тот же момент нужно начать медленно отпускать педаль сцепления левой ногой.
Это самый сложный этап для новичков, которые хотят правильно ездить на механике. Ещё раз: правую ногу перемещаем с педали тормоза на педаль газа и медленно нажимаем газ… Одновременно медленно отпускаем педаль сцепления левой ногой. Постарайтесь слегка нажать педаль газа и держать её так, чтобы стрелка тахометра показывала около 1500-2000 об./мин. В это время необходимо постепенно отпускать педаль сцепления левой ногой.
Постарайтесь слегка нажать педаль газа и держать её так, чтобы стрелка тахометра показывала около 1500-2000 об./мин. В это время необходимо постепенно отпускать педаль сцепления левой ногой.
Если всё сделано правильно, вы начнете чувствовать, что шестерни коробки передач соединятся с двигателем, в результате чего автомобиль начнет медленно двигаться вперед. Когда скорость немного вырастет, можно отпускать сцепление. Поздравляем! Теперь вы научились трогаться и ехать на первой передаче. Если двигатель заглох, начинайте всё с начала.
Переходим к остановке. Нужно не просто научиться ездить на механике, но и вовремя остановиться. Для того чтобы остановить машину с механической коробкой переключения передач, необходимо просто нажать педаль сцепления левой ногой и педаль тормоза правой ногой одновременно.
Тренируйтесь до тех пор, пока не научитесь начинать движение и ехать на первой передаче без каких-либо загвоздок. Если ничего не получается, не стоит разочаровываться, нужно просто начинать процесс снова.
Начало движения на первой передаче ничем не отличается от старта на задней передаче. Правда, в последнем случае нужно будет выбрать соответствующее положение рычага КПП. На участках с уклоном можно начинать движение даже без нажатия на педаль газа, придётся просто медленно отпустить сцепление.
Найдите горку и практикуйтесь на ней. После получения определенного опыта на ровной поверхности обязательно потренируйтесь на холме. Трогаться на подъеме намного сложнее, чем на ровном участке, поэтому уделите этому моменту достаточно времени и сил. Очень часто начинающие водители, которые только сели за руль автомобиля с механикой, попадают в неприятности, связанные с вынужденной остановкой и началом движения в пробке на участке дороги с уклоном.
Повышение передачи
Нажмите на картинку для увеличения
Как уже упоминалось ранее, человек, который научился трогаться с места и ехать на первой передаче, уже освоил около 90% техники вождения на механике. Перейти на более высокую передачу очень легко. В большинстве случаев переходить на повышенную надо после того, как стрелка тахометра достигла отметки в 3000 об./мин. Цифра может отличаться в зависимости от конкретного автомобиля, но эта информация вам не помешает. В случае слишком раннего переключения машина будет немного «дёргаться», и вам придётся перейти на более низку передачу, чтобы она не заглохла.
Перейти на более высокую передачу очень легко. В большинстве случаев переходить на повышенную надо после того, как стрелка тахометра достигла отметки в 3000 об./мин. Цифра может отличаться в зависимости от конкретного автомобиля, но эта информация вам не помешает. В случае слишком раннего переключения машина будет немного «дёргаться», и вам придётся перейти на более низку передачу, чтобы она не заглохла.
Когда вы будете готовы к включению повышенной передачи, необходимо делать все в следующем порядке:
- снять правую ногу с педали газа, полностью выжать сцепление левой ногой и передвинуть рычаг переключения КПП в требуемое положение единым движением;
- отпустить педаль сцепления и одновременно нажать на газ правой ногой;
- полностью убрать левую ногу с педали сцепления после включения более высокой передачи и продолжать держать правую ногу на педали газа.
Переход на более низкую передачу
Хотя включать пониженную передачу при остановке автомобиля на механике не нужно, в некоторых ситуациях нужно уметь делать это. Например, переключать на более низку передачу надо при движении в пробках. Переключаться необходимо в тех ситуациях, когда скорость движения снижается, а стрелка тахометра опускается до 1000 об./мин. и ниже.
Например, переключать на более низку передачу надо при движении в пробках. Переключаться необходимо в тех ситуациях, когда скорость движения снижается, а стрелка тахометра опускается до 1000 об./мин. и ниже.
Также включать более низкие передачи рекомендуется при движении по опасным дорогам, в особенности на скользком покрытии. Применение экстренного торможения приведет к заносу, а остановить машину не получится. Вместо этого гораздо лучше использовать пониженные передачи. Если дорога действительно скользкая, лучше не переключаться выше 2-3 передач.
Переключение передач без показаний тахометра
Далеко не все автомобили оснащены этим замечательным прибором. Хотя на первых порах своевременно переключать передачи на механике без тахометра очень сложно, с появлением определенных навыков, вы научитесь водить автомобиль с механической коробкой передач по звуку работы двигатель.
Если двигатель издает высокочастотный шум, и вы чувствуете, что добавление газа не приводит к получению желаемого результата, это значит, что пора переключаться на более высокую передачу. Если мотор издает низкочастотный шум и начинает вибрировать, это признак слишком высокой передачи, поэтому надо выбирать более низкую.
Нельзя ездить на механике с выжатым сцеплением
Многие новички делают ошибку, постоянно держа ногу на педали сцепления. В итоге левая нога не отдыхает. Хотя слабого давления на педаль сцепления недостаточно для того чтобы полностью отключить механизм, его вполне хватает для частичного отсоединения. Это приводит к преждевременному износу сцепления.
Вывод: после успешного перехода на выбранную передачу (или включения нейтрального положения), уберите левую ногу с педали сцепления.
Как правильно остановиться
Существует два способа остановки автомобиля на механике.
- Для замедления машины необходимо переключаться на более низкие передачи вплоть до второй, после чего нажимать на педаль тормоза.
- Нажать педаль сцепления и перевести рычаг КПП в нейтральное положение, после чего убрать левую ногу с педали сцепления и применять педаль тормоза по мере необходимости.
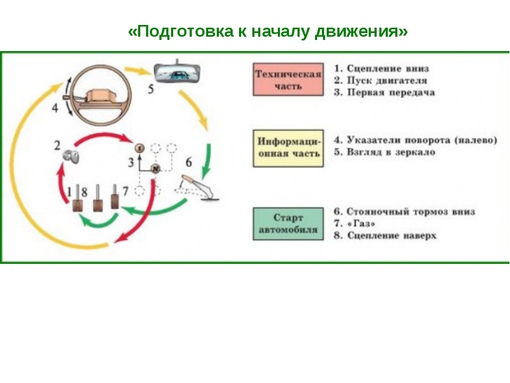
Хотя первый способ действительно можно использовать, это приведет к гораздо большему износу трансмиссии и сцепления. Гораздо легче использовать второй вариант. Переключение в нейтральное положение и работа с тормозами. Если вы не можете включить «нейтралку», не забывайте о том, что необходимо нажимать не только тормоз, но и сцепление, чтобы остановить автомобиль.
Парковка
При парковке автомобиля на механике всегда пользуйтесь ручным тормозом. Вам нужно научиться пользоваться ним каждый раз, когда вы оставляете свою машину, независимо от наклона поверхности. Для дополнительной безопасности рекомендуется оставлять автомобиль на первой передаче.
Если вы припарковались на склоне, переведите рычаг КПП в положение “R”. Не забудьте повернуть передние колеса так, чтобы в случае внезапного начала движения автомобиль не оказался на дороге.
В России пару лет назад количество автомобилей с АКПП и механической трансмиссией было примерно одинаковым, хотя предыдущие годы наблюдался бурный рост покупок транспортных средств с вариатором. Для сравнения: в США на «автоматах» ездит 94% водителей, ибо они появились гораздо раньше, чем у нас. И нетрудно догадаться, что навыки управления машиной с «механикой» там практически утеряны, чего не скажешь о РФ. Однако молодое поколение, как и женщины, уже нуждаются в подробных инструкциях того, как нужно управлять подобными авто. Но прежде, чем начинать подробное описание данного процесса, вначале нужно назвать причины, по которым машины с МКПП в России по-прежнему пользуются популярностью:
Для сравнения: в США на «автоматах» ездит 94% водителей, ибо они появились гораздо раньше, чем у нас. И нетрудно догадаться, что навыки управления машиной с «механикой» там практически утеряны, чего не скажешь о РФ. Однако молодое поколение, как и женщины, уже нуждаются в подробных инструкциях того, как нужно управлять подобными авто. Но прежде, чем начинать подробное описание данного процесса, вначале нужно назвать причины, по которым машины с МКПП в России по-прежнему пользуются популярностью:
Такими трансмиссиями всегда оснащаются мощные, спортивные автомобили;
Автомобили с механической коробкой передач стоят дешевле;
— «механика» позволяет лучше чувствовать машину и быстрее управлять ею;
Оснащение транспортного средства подобной «коробкой» позволяет экономить горючее;
В плане ремнотопригодности МКПП тоже предпочтительней в сравнении с АКПП, и стоит восстановление работоспособности агрегата значительно меньше.
Нижеследующая инструкция адресована всем желающим обучиться вождению на машине с «механикой». Причем совершенно неважно, сколько вам лет, к какому классу принадлежит транспортное средство, какова его мощность и прочее.
Причем совершенно неважно, сколько вам лет, к какому классу принадлежит транспортное средство, какова его мощность и прочее.
1. О передачах
Владея машиной с механической «коробкой», вы должны отработать навык самостоятельного переключения скоростей до автоматизма. Здесь нет электроники, которая без участия водителя уравнивает скорости вращения шестерней на валу коробки. Зато имеется педаль сцепления, которая за счет нажатия на нее ногой временно отключает трансмиссию специально для того, чтобы передвинуть рычаг в нужное положение и переключить скорость. Только помните: выжимать эту педаль нужно до конца! Кстати, основная масса машин оснащается 4-5- скоростными МКПП, дополнительно есть одна задняя скорость. Давайте разберемся, для чего они нужны.
«Нейтралка». нельзя практиковать до того, как вы разберетесь с тем, какие есть органы управления и что такое нейтральная передача. В сущности, это позиция рычага переключения скоростей, обозначающая, что крутящий момент не передается от двигателя на колеса, и тронуться с места автомобиль не может. Как вы ни газуйте, ничего не произойдет. Если же передвинуть рычаг в другую позицию при отключенном сцеплении, то включится скорость.
Как вы ни газуйте, ничего не произойдет. Если же передвинуть рычаг в другую позицию при отключенном сцеплении, то включится скорость.
Первая скорость предназначена для трогания. При этом двигатель работает на повышенных оборотах, но скорость более 15-20 км в час вы не разовьете. Да это и не нужно, вы просто сожжете лишнее топливо. Поэтому практически сразу же нужно включать вторую передачу.
Вторая скорость — это рабочая лошадка, которая позволяет спускаться со склона и маневрировать в дорожной «пробке». Она является переходной к так называемым пониженным 3-5 передачам, позволяющим развивать более высокую скорость. Акцентироваться на них мы не будем, так как переключаются они одинаково.
Задняя передача позволяет развить большую скорость в сравнении с первой. Однако долго двигаться с ее помощью не рекомендуется — слишком быстро изнашиваются детали трансмиссии. Без задней передачи практически невозможно в городских условиях припарковаться, также она позволяет маневрировать в органическом пространстве.
2. Процесс освоения передач
Расположение скоростей указаны на ручке их переключения, и их нужно просто вызубрить! Согласитесь, что во время езды будет трудновато подсматривать, опуская глаза вниз. И еще: если не хотите, чтобы любая передача включалась со скрежетом либо хрустом, сигнализирующем об износе шестерен, выжимайте педаль сцепления до пола. А еще лучше перед посадкой за руль сесть на переднее сиденье рядом с опытным водителем и проследить, как ему удается синхронизировать переключение передач с отключением сцепления. Также это поможет вам изучить, какую скорость можно развить на конкретной передаче.
На механике для начинающих показывают, что новички на первых порах все равно мысленно вспоминают, где какая передача находится. Не волнуйтесь, дальнейшая практика позволит вам это делать на бессознательном уровне, без отвлечения от дороги. Пройдет совсем немного времени — увеличится и скорость переключения, и плавность данного процесса.
Также безусловной проблемой для молодого водителя является определение того, при какой скорости движения автомобиля нужно включать ту или иную передачу. Обычно нужно следовать простому совету: слушайте двигатель, и если его обороты низкие, а машина не разгоняется — значит, следует перейти на понижающую передачу. И наоборот, чтобы разгрузить коробку при очень больших оборотах, нужно включить повышенную передачу.
Обычно нужно следовать простому совету: слушайте двигатель, и если его обороты низкие, а машина не разгоняется — значит, следует перейти на понижающую передачу. И наоборот, чтобы разгрузить коробку при очень больших оборотах, нужно включить повышенную передачу.
В этой практике можно пользоваться тахометром, если он имеется «на борту». Конечно, в зависимости от модели, марки и модификации автомобиля порядок переключения может быть разным, однако доказано на практике, что новая передача должна задействоваться тогда, когда обороты мотора достигли 3000 об./мин. Дополнительно рекомендуется наблюдать за спидометром. Например, переключайте скорости каждые 20-25 км/ч, однако помните, что это общее правило. Если у авто мощный мотор, то эти цифры могут быть однозначно большими.
3. Запускаем двигатель!
Перед тем, как повернуть ключ зажигания для запуска мотора, нажмите педаль сцепления и переведите рычаг МКПП на «нейтралку». Далее нужно прогреть силовой агрегат до рабочей температуры.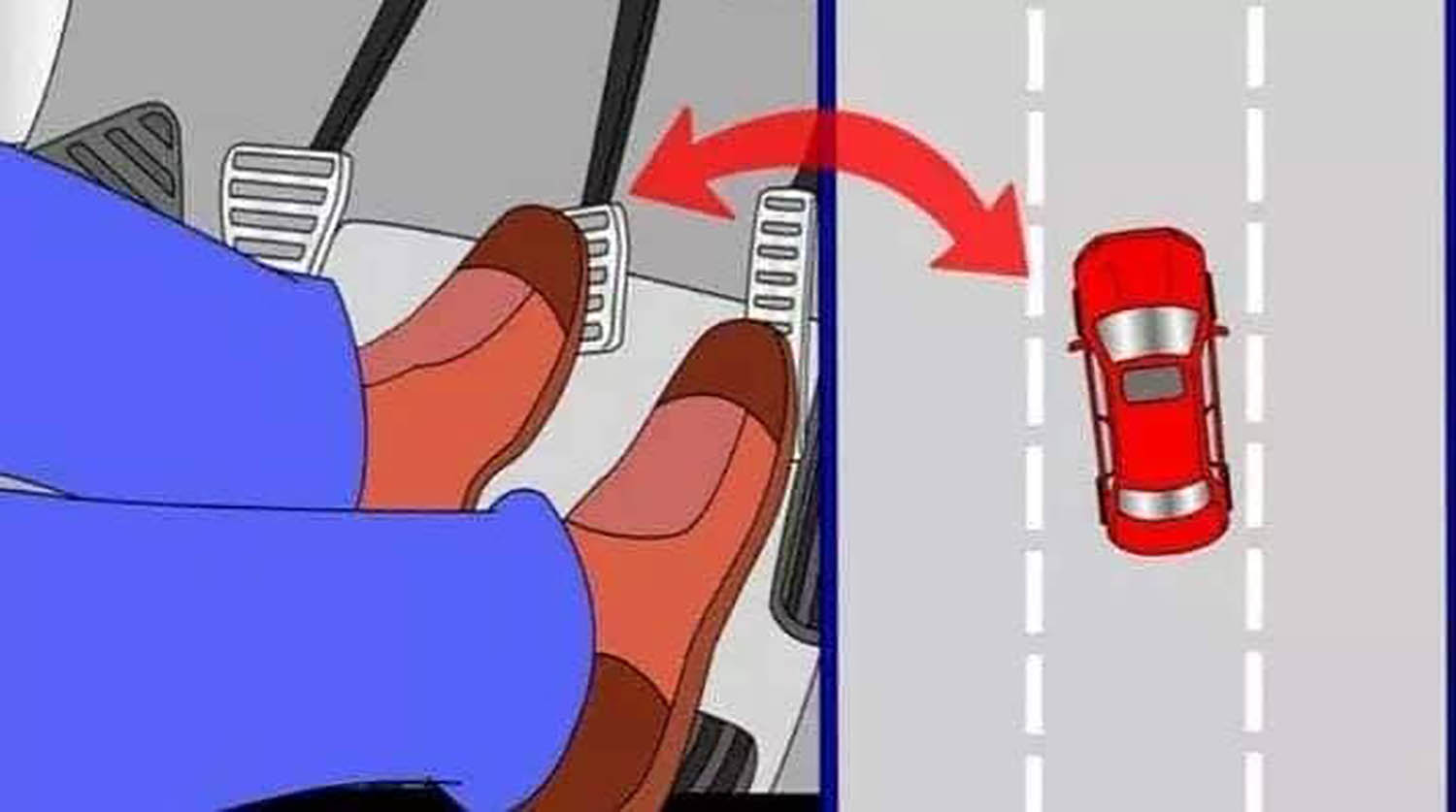 Причем если вы делаете это в холодную пору года, первые пару минут во время прогрева держите педаль сцепления в нажатом положении — это помогает быстрее нагреть застывшее масло. И самое главное: никогда не запускайте мотор с включенной передачей , иначе машина может поехать, к чему вы вряд ли будете готовы. Так и до ДТП недалеко…
Причем если вы делаете это в холодную пору года, первые пару минут во время прогрева держите педаль сцепления в нажатом положении — это помогает быстрее нагреть застывшее масло. И самое главное: никогда не запускайте мотор с включенной передачей , иначе машина может поехать, к чему вы вряд ли будете готовы. Так и до ДТП недалеко…
4. Педаль сцепления используем правильно
Как уже было сказано, сцепление помогает водителю плавно переключать скорости, но его всегда следует выжимать до конца, иначе вы рискуете повредить коробку. Не менее важно запомнить, что педалью сцепления должна заниматься исключительно левая нога. Правая нужна вам для торможения или набора скорости. Уроки вождения на механике для начинающих редко обходятся без ситуаций, когда новичок «путает педали». Стоит ли говорить, что лучше их избегать?
После переключения передачи сцепление следует отпускать плавно. На первых порах это делать нелегко. Совет: отпускайте сцепление очень медленно до той поры, пока не почувствуете появление крутящего момента, передаваемого на колеса. И избегайте ненужных ускорений в ситуациях, когда педаль нажата не до «пола». Также выработайте «железное» правило, которое гласит: даже на светофорах держать сцепление отжатым более двух секунд крайне не рекомендуется.
И избегайте ненужных ускорений в ситуациях, когда педаль нажата не до «пола». Также выработайте «железное» правило, которое гласит: даже на светофорах держать сцепление отжатым более двух секунд крайне не рекомендуется.
Если понаблюдать за опытными водителями, то нетрудно заметить, что они отпускают сцепление достаточно быстро. Если у вас так не получается, не комплексуйте. Чем чаще вы будете ездить в плотном траффике, чем больше накатаете часов вождения — тем совершеннее станет этот навык.
5. Учимся координировать действия
Машина с МКПП при умелом управлении доставляет водителю массу немало драйва. Ведь она предоставляет возможность резкого ускорения, что недоступно машине с АКПП. помогают довести это действия до автоматизма, четко координируя манипуляции с органами управления. Приведем пример правильного алгоритма при езде на 1-2 скоростях.
Выжмите до упора педаль сцепления, включите первую передачу. Постепенно медленно отпускайте сцепление, одновременно столь же медленно и плавно нажимайте на педаль газа. Когда педаль сцепления дойдет примерно до середины, вы наверняка почувствуете, что крутящий момент стопроцентно передается на колеса и автомобиль начинает движение. Плавно отпустите сцепление и продолжая плавно нажимать на газ, набирите скорость около 20 км/ч. Теперь самое время включить вторую передачу. Отпустите газ, полностью выжмите сцепление и передвиньте рычаг МКПП на вторую передачу, отпустите сцепление и плавно прибавляйте газ.
Когда педаль сцепления дойдет примерно до середины, вы наверняка почувствуете, что крутящий момент стопроцентно передается на колеса и автомобиль начинает движение. Плавно отпустите сцепление и продолжая плавно нажимать на газ, набирите скорость около 20 км/ч. Теперь самое время включить вторую передачу. Отпустите газ, полностью выжмите сцепление и передвиньте рычаг МКПП на вторую передачу, отпустите сцепление и плавно прибавляйте газ.
6. Дауншифтинг
Под этим странным термином подразумевается то, как переключать низкие передачи машины в момент ее замедления. Метод здесь совершенно другой в сравнении с принципами работы коробки-автомата, он сложнее, но позволяет не просто снизить скорость, но и одновременно включить необходимую передачу.
Зачем уроки вождения на механике для начинающих включают в себя умение «дауншифтить»?
Они нужны, чтобы научиться снижать скорость до полной остановки без применения педали тормоза. Как говорят профи, можно тормозить и двигателем. Чтобы это сделать на скорости примерно в 70 км/ч, совершите следующие манипуляции:
Чтобы это сделать на скорости примерно в 70 км/ч, совершите следующие манипуляции:
выжав сцепление, включите третью передачу, передвинув правую ногу с акселератора на тормоз;
медленно отпускайте сцепление — это позволит избежать повышенных оборотов;
перед остановкой повторно выжмите сцепление;
первую скорость в качестве понижающей не активируйте.
7. Задний ход
В обращении с задней передачи следует быть осторожным, так как если ее включить неправильно, она может «выскочить». И пока транспортное средство полностью не остановилось, никогда не включайте движение задним ходом! Также учитывайте, что в некоторых легковых авто для манипуляции с нею нужно сначала нажать сверху на ручку МКПП. Не будем забывать и о высоком диапазоне работы задней передачи в сравнении с первой, из чего следует: давить на педаль газа не следует, ибо вы можете набрать излишне высокую скорость.
8. Трогание в гору
Поскольку автодороги весьма редко являются идеально плоскими, умение управлять машиной, стоящей под вертикальным углом, является весьма нелишним. Навыки в данном случае тоже вырабатываются практикой, однако добиться желаемого результата сложнее. Алгоритм действий таков.
Навыки в данном случае тоже вырабатываются практикой, однако добиться желаемого результата сложнее. Алгоритм действий таков.
1) Загоните автомобиль на наклонный участок дороги, поставьте на ручной тормоз, включите «нейтралку».
2) Постепенно отпуская ручник, выжмите педаль сцепление, перейдите на первую передачу и трогайтесь, добавив газа.
3) В определенный момент вы почувствуете: машина назад не съезжает. Значит, вам удалось удержать авто на горке, не применяя тормоз.
9. Тайны парковки
При постановке машины на парковку после глушения мотора нужно, выжав сцепление, активировать первую передачу. Можете быть уверены: благодаря этому авто не скатится ни в коем случае. Чтобы еще больше обезопаситься, нужно включить стояночный тормоз, потянув ручку или нажав кнопку. Самое главное по возвращению к машине — не забыть включить нейтральную передачу, и только потом включать двигатель.
10. Практикуйтесь чаще!
Уроки вождения на механике для начинающих поначалу кажутся чрезвычайно тяжелыми. И это нормально. Но чем больше вы будете практиковаться, тем скорее до автоматизма отработаете буквально все навыки. И если «права» уже на руках, а садиться за руль страшновато — найдите удобную площадку, где нет машин, и занимайтесь самостоятельно.
И это нормально. Но чем больше вы будете практиковаться, тем скорее до автоматизма отработаете буквально все навыки. И если «права» уже на руках, а садиться за руль страшновато — найдите удобную площадку, где нет машин, и занимайтесь самостоятельно.
Когда вы почувствуете, что более-менее приспособились к авто с «механикой», переходите к практическому опыту в реальных дорожных условиях. Начинайте с простых упражнений, предварительно изучив местность, по которой вы будете ездить чаще всего. Рекомендуется заниматься рано-рано утром, часов в 5, либо после полуночи — в это время машин на дороге меньше всего, что придаст дополнительную уверенность.
И не слушайте знакомых или родственников, которые говорят, что механическая коробка передач — это архаизм, устаревшие технологии, риск и так далее. Помните: «механика» в автомире считается одной из самых надежных. Безусловно, иногда она снижает комфортность вождения, но наградой за это становится повышенная мощность, топливная экономичность, низкая цена на ремонт. И самое главное: вы приобретете бесценный жизненный опыт и умение стопроцентно контролировать транспортное средство!
И самое главное: вы приобретете бесценный жизненный опыт и умение стопроцентно контролировать транспортное средство!
Привет, друзья! Сегодня я, Евгений Борисов, предлагаю поговорить о вождении автомобиля с механической трансмиссией.
Как часто вы замечали, что на светофоре учебный автомобиль превращается в дикого мустанга: при попытке тронуться просто-напросто глохнет?
Отсутствием плавного старта и большим откатом назад страдают многие новички, но с опытом эта проблема уходит.
Зато приходит понимание, как правильно ездить на механике и как реже посещать автосервисы. Поехали!
Я не волшебник! Я только учусь!
Опытные водители, которые попробовали и механику, и автомат наверняка со мной согласятся – с механической коробкой без опыта ездить сложнее.
Именно поэтому всем, кто только постигает азы вождения, я бы рекомендовал начать обучение именно с нее. После механической коробки вам сам черт не страшен!
Основная сложность для новичков, особенно женского пола, – в невозможности поймать «тот самый момент», когда «сцепление плавно отпускается», а «газ выжимается». И хотя на словах объяснять подобные вещи сложно, попробуем слегка прояснить.
И хотя на словах объяснять подобные вещи сложно, попробуем слегка прояснить.
- Еще до начала запуска двигателя, выжмите сцепление до упора левой ногой, а правой – тормоза. Заведите авто, убедившись, что передача выключена (иначе машина может поехать).
- Переведите рычаг переключения КПП (под вашей правой рукой) на 1 скорость. И упаси вас бог, сделать подобное при невыжатом сцеплении. После одного раза, может, трагедии и не случится, но при регулярном нарушении правила придется платить за ремонт.
- Переведите правую ногу с тормоза на газ. Плавно отпускайте сцепление и одновременно начинайте утапливать педаль газа. Вы почувствуете, как шестерни трансмиссии «зацепились», а автомобиль «покатился». Следите, чтобы тахометр показывал примерно 2 тыс. оборотов в минуту.
- Не бросайте сцепление резко, иначе заглохните. Делайте всё плавно, словно вы – шаолиньский монах во время медитации.
- При наборе скорости – медленно отпускайте сцепление.
Поспешу приправить инструкцию, от которой вы, вполне возможно, слегка приуныли, порцией позитива: если вы научитесь трогаться с места – считайте, что освоили механику на 80%.
На заметку! Хороший инструктор будет настаивать на четком закреплении ног за той или иной педалью: для сцепления и тормоза – левая, для газа – правая.
Учиться лучше всего на автодроме с ровным покрытием, где вас не будут смущать другие водители (а они, ох, какую нетерпимость проявляют иногда на дорогах).
После того как вы научитесь трогаться, двигаться и останавливаться на площадке, вас «выведут в люди» – предложат прокатиться по городу. Главный совет – не обращайте внимания на недовольные взгляды и «бибиканье».
Просто делайте своё дело, успокаивая себе тем, что рядом инструктор, который, в случае чего, придет на помощь.
Скоростной режим
Сложность с переключением скоростей преодолеть проще, чем научиться плавно трогаться. Как только стрелка тахометра приблизиться к отметке 3 тыс. об/мин:
- отпустите газ, до упора выжмите сцепление и передвиньте рычаг в новое положение (например, на вторую скорость – она, кстати, считается самой рабочей и используется чаще других) – все эти операции делаются синхронно;
- плавно отпускайте сцепление и выжимайте газ (точно так же как вы делали на этапе начала движения).

На заметку! Если во время переключения скорости автомобиль начинает «трясти», то вы поторопились.
Строго говоря, на механике переходить на более низкую передачу перед остановкой машины не нужно, однако в некоторых случаях, например, при движении в пробках, уйти на пониженную передачу целесообразно, чтобы уменьшить расход топлива.
На обледеневших покрытиях зимой и опасных участках также лучше использовать низкие передачи – уходить на них нужно при показаниях тахометра менее тысячи об/мин.
А что делать, если в авто нет тахометра? Инструкторы часто предлагают «слушать» – если мотор «басит», а автомобиль при этом не едет быстрее, то включена слишком высокая передача.
Вот только тем, кто сидит месяц за рулем, очень часто сложно различить «симфонию», поэтому можно ориентироваться на спидометр:
- до 25 км/час – 1-я передача;
- от 25 до 50 – 2-я;
- от 50 до 70 – 3-я.
Смотрите полезные видео уроки, которые я специально подобрал для вас по теме разговора.
Ошибки новичков
Многие начинающие полагают, что намного проще держать сцепление выжатым постоянно, чем ломать голову, когда на педаль нажимать, а когда нет. В этом случае не избежать вам двух зол:
- затекшей левой ноги, которую от постоянного напряжения начнет сводить или «пронзать иголками»;
- преждевременной «смерти» сцепления.
Ногу, конечно, после остановки можно растереть и «привести в чувство», но если вы не хотите ездить исключительно до мастерской, чтобы не сжечь сцепление, убирайте ногу с педали после каждой операции.
Итак, ездить мы научились, но ведь надо еще понять, как останавливаться.
Неопытные водители часто просто сбрасывают скорость, переводят рычаг в нужное положение и жмут на тормоз, хотя такой вариант быстро изнашивает и сцепление, и саму коробку.
Правильный вариант торможения и остановки:
- выжать сцепление;
- перевести рычаг в нейтралку;
- снять ногу со сцепления;
- плавно давить на тормоз до полной остановки.

На заметку! При нейтралке крутящий момент не передается на колеса, это значит, что даже заведенный автомобиль при нейтральной передаче в случае нажатия газа не поедет.
И еще одна распространенная ошибка начинающих – игнорирование ручного тормоза. Использовать ручник нужно каждый раз, когда вы паркуетесь, независимо от угла наклона поверхности.
Дополнительно защитить от «укатывания в бездну» поможет и переведение рычага в положение первой скорости. Если вы остановились на склоне, то выставьте рычаг на «R» и поверните передние колеса.
Повторюсь, можно теоретически вызубрить, как научиться правильно ездить на механике, но без практических навыков и хорошего инструктора, вы даже тронуться с места не сможете. Хотите поспорить?
Выбирая для себя автомобиль, будущие водители становятся перед выбором: какую выбрать марку машины, цвет, тип кузова, а также с механической коробкой передач, либо с АКПП.
Все зависеть будет от личных предпочтений и материальных возможностей. Ведь автомобили с МКПП будут стоить на порядок дешевле, нежели автомат. Но не все знают, как правильно ездить на механике.
Ведь автомобили с МКПП будут стоить на порядок дешевле, нежели автомат. Но не все знают, как правильно ездить на механике.
Для чего нужно умение вождения авто с механической коробкой?
Некоторые автошколы предоставляют такие услуги, как обучение вождению исключительно на автомобили автомат. Это значит, что и права будут выданы соответствующие. То есть, потом сесть за руль МКПП не представится возможным без получения нового удостоверения.
Ситуации в жизни возникают различные, и иногда возникает острая необходимость управлять автомобилем с механической коробкой. Получив права, позволяющие это делать, всегда можно пересесть на автомат. Наоборот же, сделать не получится.
Покупка авто на механике является более выгодным приобретением. Помимо более низкой цены автомобилей, их эксплуатация выйдет также более экономичной. Как правило, расход топлива у них меньший, и ремонт некоторых деталей выйдет также менее дорогим.
В ситуации, когда оказывается разряженным аккумулятор, можно выйти из положения. Например, перекинуть провода из другого автомобиля для подзарядки. Либо же машина может завестись, с так называемого толкача. Эти варианты не подходят, если транспортное средство с автоматической трансмиссией.
Например, перекинуть провода из другого автомобиля для подзарядки. Либо же машина может завестись, с так называемого толкача. Эти варианты не подходят, если транспортное средство с автоматической трансмиссией.
Только используя механическую коробку, можно чувствовать полный контроль над автомобилем. Когда многие манипуляции выполняются на автомате, этого не происходит.
Основы езды на механике
Прежде чем узнать, как научиться ездить на механике, желательно понимать, с чем вообще придется иметь дело:
- Педали. При управлении ТС используется три педали: газ (крайняя правая), тормоз (по центру), сцепление (располагается слева). В отличие от автоматической трансмиссии, здесь используются в управлении обе ноги. Если водитель, севший за руль механики новичок, поначалу, это делать будет непривычно.
- КПП. При помощи смещения шестеренок в трансмиссии, происходит переключение скоростей. На многих автомобилях данный селектор оснащен подсказками, используя которые проще разобраться, какая передача выбрана.

- Тахометр. Располагается на панели приборов, и позволяет определить, сколько коленвал двигателя делает оборотов в минуту. При помощи него новички контролируют, когда необходимо переключаться на следующую передачу.
Разбираемся с передачами на МКПП
Механика тем и отличается от автомата, что требует постоянного контроля водителя, то есть, самостоятельного переключения скоростей. В основном ТС имеют 4 или 5 скоростей, и в дополнении к ним задняя. Чтобы понимать месторасположение каждой, необходимо знать их предназначение.
Коробка передач: инструкция для начинающих
- Всякий раз движение начинается с выжима педали сцепления, таким образом, появляется возможность переходить на другую скорость. Вводить требуемую передачу допустимо в том случае, когда сцепление будет полностью выжато.
- Когда избрана нейтральная передача, при выжимании газа, автомобиль не двинется с места. Когда селектор находится в данной позиции, возможно, выбирать желаемую скорость, включая заднюю.

- Рабочей передачей считается вторая. На ней удобно передвигаться по наклонной местности, а также осуществлять езду в пробках. Первую же обычно используют для старта пути, затем, ускоряясь, переходят на вторую. Набрав еще большую скорость и обороты, можно переходить на третью.
- Труднее освоить неопытным водителям как ездить на механике, на задней передаче. Используя ее, разгон происходит быстрее, нежели на первой, но все же, водить машину часто, таким образом, весьма опасно.
Прежде чем выезжать на автомобиле в город, необходимо хорошо ориентироваться, где какая передача расположена. Теория это хорошо, но в данном случае, необходимы практические навыки. Ведь во время езды отвлекаться и смотреть на селектор, выбирая нужную передачу, нельзя, поскольку это небезопасно. Первое время можно тренироваться на авто, в нерабочем состоянии, доводить до автоматизма включение передач.
Начало движения
Порядок действий:
- Прежде чем, повернуть ключ в замке зажигания, необходимо полностью выжать педаль сцепления левой ногой, а правой нажать на тормоз, и только после этого завести мотор.
 Мотор заведен, сцепление выжато, можно включать первую передачу (до этого селектор находиться в нейтральном положении). Чтобы автомобиль не заглох, нельзя отпускать левую ногу с педали. Когда машина работает, с тормоза, нога перемещается на педаль газа и одновременно необходимо начинать убирать ногу со сцепления, только плавно.
Мотор заведен, сцепление выжато, можно включать первую передачу (до этого селектор находиться в нейтральном положении). Чтобы автомобиль не заглох, нельзя отпускать левую ногу с педали. Когда машина работает, с тормоза, нога перемещается на педаль газа и одновременно необходимо начинать убирать ногу со сцепления, только плавно. - Чтобы выполнить переход на следующую скорость, необходимо, чтобы стрелка тахометра приравнивалась к 3000 оборотам. Если переключиться слишком рано, то машина может заглохнуть.
Как выполняется переход:
- Правая нога убирается с газа, а левой полностью выжимается сцепление, и в это время селектор переводится в необходимое положение,
- Сцепление необходимо отпустить, а педаль газа нажать,
- Далее в управлении участвует только правая нога, до перехода на следующую скорость или остановки.
Более опытные водители обычно не обращают внимания на показания тахометра, а ориентируются на звук двигателя.
Если автомобиль не разгоняется и слишком низкие обороты, то необходимо переключиться на скорость ниже.
А если же обороты слишком высокие, то необходимо включение следующей скорости, чтобы не перегружать двигатель.
Остановка и парковка
Чтобы заглушить автотранспорт можно использовать два варианта:
- Переключение на пониженные передачи, вслед за тем, необходимо выжать педаль тормоза.
- Надавить сцепление и переместить селектор в нейтральную позицию, затем устранить ногу со сцепления и поднажать, если есть надобность, тормоз.
Чтобы износ коробки был меньшим лучше использовать второй способ, и не забывать помимо тормоза обязательно выжимать сцепление.
Припарковав свой автомобиль всегда необходимо использовать ручной тормоз, особенно, если поверхность с наклоном. Также всегда стоит помнить о положении колес во время стоянки. Их требуется выворачивать таким образом, чтобы в случае внезапного движения, машина не очутилась на проезжей части.
Как быстро научиться ездить на машине с механической коробкой передач
Главная » Разное » Как быстро научиться ездить на машине с механической коробкой передачВождение на механике – основные моменты
Впервые сел за руль автомобиля с механической трансмиссией и не знаешь, как вообще начать движение? Не умеешь вовремя переключать скорости на механике? Ответы на все эти, а также другие вопросы, которые очень часто интересуют начинающих водителей, вы сможет найти в нашей сегодняшней статье.
Почему нужно уметь водить машину на механике
Вы никогда не знаете, в какую ситуацию попадёте в ближайшее время. Возможно, вам придётся одолжить чужой автомобиль, который будет оснащен механической коробкой передач. Или ваш друг захочет выпить, и обратится к вам с просьбой доставить его домой на его же авто с МКПП? А что с прокатом автомобилей за рубежом? Машины на механике встречаются намного чаще, нежели авто с АКПП.
Если вы научитесь ездить на механике, вас ничто не застанет врасплох. Человек, который понимает, как ездить на автомобиле с механической трансмиссией, с легкостью сядет за руль машины с «автоматом», но не наоборот.
Машины с ручной трансмиссией, в большинстве случаев, стоят меньше, чем аналогичные версии с АКПП. Вы сэкономите деньги не лишь при покупке автомобиля. Вождение на механике – это серьезная экономия средств в течение многих лет эксплуатации транспортного средства, поскольку расход топлива таких автомобилей очень часто является меньшим, по сравнению с автоматическими трансмиссиями.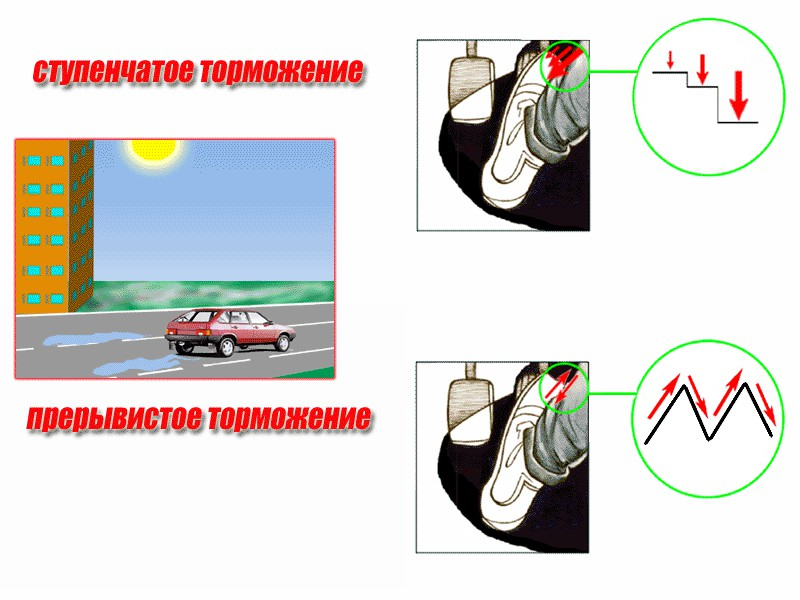 Поскольку цены на топливо неумолимо растут, выгода будет очевидной.
Поскольку цены на топливо неумолимо растут, выгода будет очевидной.
Если аккумулятор вашего автомобиля с МКПП разрядился, вы сможете начать движение. Один из вариантов – воспользоваться проводами для прикуривания. Если их под рукой не оказалось, всегда можно завести машину “с толкача”. Забудьте об этой идее, если вы используете автомобиль с автоматической трансмиссией.
Многие спорткары доступны исключительно с механической трансмиссией. В особенности это касается многих моделей, выпущенных несколько десятков лет назад. В большинстве случаев производители таких машин понимают, что получить истинное удовольствие от вождения мощного авто можно лишь с механической КПП.
Водить машину на механике гораздо веселее! Если вы всю жизнь проездите на АКПП, вы так и не узнаете, что такое настоящий контроль над автомобилем. Езда на машине с «автоматом» очень искусственная и пассивная. А вот механика позволяет вам стать с автомобилем одним целым.
Как правильно ездить на механике: основы
Первое: познакомиться с местом водителя
Педали: сцепление, тормоз, газ. Педаль сцепления расположена слева, её нет на автомобилях с автоматической коробкой передач. Её надо нажимать при переключении передач вверх или вниз. Больше информации будет далее.
Педаль тормоза расположена по центру. Как вы, наверное, понимаете, она создана для торможения.
Крайняя правая педаль – это газ. Функционирует по тому же принципу, что и педаль газа в машине с АКПП.
Людям, которые впервые садятся в автомобиль с механической коробкой, трудно привыкнуть к тому, что теперь надо пользоваться ещё и левой ногой. Ведь в машинах с «автоматом» задействована лишь правая нога. Левая нога будет нажимать педаль сцепления, а правая нога – отвечать за тормоз и газ.
Рычаг переключения коробки передач. Именно с помощью него будем переключать передачи, он смещает шестерни в трансмиссии автомобиля. Многие новые автомобили с ручной коробкой оснащаются шестью передачами. Как правило, на ручке переключения КПП имеется подсказка, с помощью которой вы сможете понять, какие позиции рычага отвечают за определенную передачу. Это поможет вам правильно водить машину на механике.
Тахометр. Это один из элементов приборной панели автомобиля, который отображает количество оборотов в минуту коленвала двигателя. Когда вы только начинаете водить автомобиль с механической коробкой передач, тахометр поможет вам определить, когда именно надо переключаться вверх или вниз. В большинстве случаев необходимо включать более высокую передачу, когда стрелка тахометра достигает “3” или 3000 об./мин. Если же она опускается до отметки “1” или 1000 об./мин, необходимо переключаться вниз. После получения некоторого опыта вождения на механике вы сможете с легкостью определить, когда именно надо переключаться, реагируя на звук работы мотора. Больше об этом читайте ниже.
Переключение скоростей и нажатие педалей сцепления и газа на выключенном двигателе
Перед тем как начать применять дальнейшие советы на практике советуем потренироваться делать всё с выключенным двигателем и включенным стояночным тормозом. Это поможет вам почувствовать зацепление и расцепление шестерней трансмиссии. Также вы сможете научиться плавно нажимать педаль сцепления.
Это поможет вам почувствовать зацепление и расцепление шестерней трансмиссии. Также вы сможете научиться плавно нажимать педаль сцепления.
Как тронуться с места на автомобиле с МКПП
Вероятно, самая пугающая часть процесса обучения вождению машины на механике – это начало движения на первой передаче. Вам понадобится некоторое время, чтобы понять, как лучше отпускать сцепление и нажимать на газ, чтобы поймать тот самый оптимальный момент и начать движение.
Практиковаться лучше на пустой стоянке. Покрытие должно быть ровным, наличие каких-либо иных транспортных средств поблизости крайне нежелательно. Желательно, чтобы на переднем пассажирском кресле находился человек, который четко понимает и умеет правильно ездить на механике.
Нажмите на педали сцепления и тормоза, после чего запустите двигатель. Чтобы завести автомобиль с механической коробкой всегда нажимайте сцепление ещё до того как будете включать зажигание. Хотя держать правую ногу на педали тормоза при запуске мотора в машине на механике необязательно (как это делают в автомобилях с автоматической трансмиссией), эта привычка вам не помешает.
Левая нога полностью выжимает педаль сцепления, а правая нога нажимает на тормоз. Заводим машину.
Включение 1-й передачи. Переводим рычаг переключения КПП в положение, соответствующее первой передачи.
Ни в коем случае не переключайте передачи до тех пор, пока педаль сцепления не выжата полностью!
Если вы не будете придерживаться этого простого правила, то услышите очень неприятный скрежет. Если ситуация будет повторяться неоднократно, вам придётся ехать к автомобильному мастеру. Убедитесь в том, что ваша левая нога, по-прежнему, выжала педаль сцепления до упора, после чего включайте 1-ю передачу.
Для этого надо использовать правую руку и переместить рычаг переключения передач вверх и влево.
Убедитесь в том, что передача действительно включена. Это можно легко почувствовать, а также увидеть. Рычаг должен оставаться на месте после того, как вы уберёте от него руку.
Держите ноги на педалях сцепления и тормоза, полностью выжав их. Не снимайте левую ногу с педали, в противном случае автомобиль заглохнет. Переместите правую ногу с педали тормоза на педаль газа. Приблизительно в тот же момент нужно начать медленно отпускать педаль сцепления левой ногой.
Не снимайте левую ногу с педали, в противном случае автомобиль заглохнет. Переместите правую ногу с педали тормоза на педаль газа. Приблизительно в тот же момент нужно начать медленно отпускать педаль сцепления левой ногой.
Это самый сложный этап для новичков, которые хотят правильно ездить на механике. Ещё раз: правую ногу перемещаем с педали тормоза на педаль газа и медленно нажимаем газ… Одновременно медленно отпускаем педаль сцепления левой ногой. Постарайтесь слегка нажать педаль газа и держать её так, чтобы стрелка тахометра показывала около 1500-2000 об./мин. В это время необходимо постепенно отпускать педаль сцепления левой ногой.
Если всё сделано правильно, вы начнете чувствовать, что шестерни коробки передач соединятся с двигателем, в результате чего автомобиль начнет медленно двигаться вперед. Когда скорость немного вырастет, можно отпускать сцепление. Поздравляем! Теперь вы научились трогаться и ехать на первой передаче. Если двигатель заглох, начинайте всё с начала.
Переходим к остановке. Нужно не просто научиться ездить на механике, но и вовремя остановиться. Для того чтобы остановить машину с механической коробкой переключения передач, необходимо просто нажать педаль сцепления левой ногой и педаль тормоза правой ногой одновременно.
Тренируйтесь до тех пор, пока не научитесь начинать движение и ехать на первой передаче без каких-либо загвоздок. Если ничего не получается, не стоит разочаровываться, нужно просто начинать процесс снова.
Начало движения на первой передаче ничем не отличается от старта на задней передаче. Правда, в последнем случае нужно будет выбрать соответствующее положение рычага КПП. На участках с уклоном можно начинать движение даже без нажатия на педаль газа, придётся просто медленно отпустить сцепление.
Найдите горку и практикуйтесь на ней. После получения определенного опыта на ровной поверхности обязательно потренируйтесь на холме. Трогаться на подъеме намного сложнее, чем на ровном участке, поэтому уделите этому моменту достаточно времени и сил.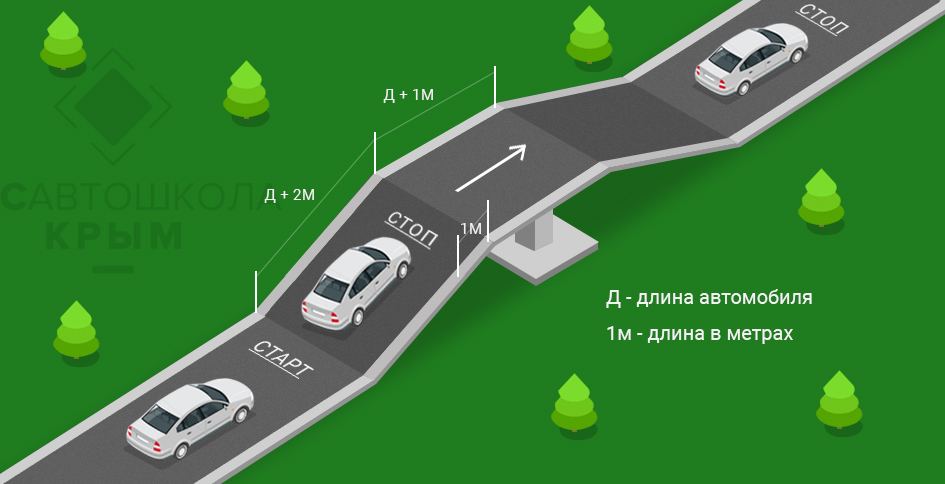 Очень часто начинающие водители, которые только сели за руль автомобиля с механикой, попадают в неприятности, связанные с вынужденной остановкой и началом движения в пробке на участке дороги с уклоном.
Очень часто начинающие водители, которые только сели за руль автомобиля с механикой, попадают в неприятности, связанные с вынужденной остановкой и началом движения в пробке на участке дороги с уклоном.
Повышение передачи
Нажмите на картинку для увеличения
Как уже упоминалось ранее, человек, который научился трогаться с места и ехать на первой передаче, уже освоил около 90% техники вождения на механике. Перейти на более высокую передачу очень легко. В большинстве случаев переходить на повышенную надо после того, как стрелка тахометра достигла отметки в 3000 об./мин. Цифра может отличаться в зависимости от конкретного автомобиля, но эта информация вам не помешает. В случае слишком раннего переключения машина будет немного «дёргаться», и вам придётся перейти на более низку передачу, чтобы она не заглохла.
Когда вы будете готовы к включению повышенной передачи, необходимо делать все в следующем порядке:
- снять правую ногу с педали газа, полностью выжать сцепление левой ногой и передвинуть рычаг переключения КПП в требуемое положение единым движением;
- отпустить педаль сцепления и одновременно нажать на газ правой ногой;
- полностью убрать левую ногу с педали сцепления после включения более высокой передачи и продолжать держать правую ногу на педали газа.
Переход на более низкую передачу
Хотя включать пониженную передачу при остановке автомобиля на механике не нужно, в некоторых ситуациях нужно уметь делать это. Например, переключать на более низку передачу надо при движении в пробках. Переключаться необходимо в тех ситуациях, когда скорость движения снижается, а стрелка тахометра опускается до 1000 об./мин. и ниже.
Также включать более низкие передачи рекомендуется при движении по опасным дорогам, в особенности на скользком покрытии. Применение экстренного торможения приведет к заносу, а остановить машину не получится. Вместо этого гораздо лучше использовать пониженные передачи. Если дорога действительно скользкая, лучше не переключаться выше 2-3 передач.
Переключение передач без показаний тахометра
Далеко не все автомобили оснащены этим замечательным прибором. Хотя на первых порах своевременно переключать передачи на механике без тахометра очень сложно, с появлением определенных навыков, вы научитесь водить автомобиль с механической коробкой передач по звуку работы двигатель.
Если двигатель издает высокочастотный шум, и вы чувствуете, что добавление газа не приводит к получению желаемого результата, это значит, что пора переключаться на более высокую передачу. Если мотор издает низкочастотный шум и начинает вибрировать, это признак слишком высокой передачи, поэтому надо выбирать более низкую.
Нельзя ездить на механике с выжатым сцеплением
Многие новички делают ошибку, постоянно держа ногу на педали сцепления. В итоге левая нога не отдыхает. Хотя слабого давления на педаль сцепления недостаточно для того чтобы полностью отключить механизм, его вполне хватает для частичного отсоединения. Это приводит к преждевременному износу сцепления.
Вывод: после успешного перехода на выбранную передачу (или включения нейтрального положения), уберите левую ногу с педали сцепления.
Как правильно остановиться
Существует два способа остановки автомобиля на механике.
- Для замедления машины необходимо переключаться на более низкие передачи вплоть до второй, после чего нажимать на педаль тормоза.

- Нажать педаль сцепления и перевести рычаг КПП в нейтральное положение, после чего убрать левую ногу с педали сцепления и применять педаль тормоза по мере необходимости.
Хотя первый способ действительно можно использовать, это приведет к гораздо большему износу трансмиссии и сцепления. Гораздо легче использовать второй вариант. Переключение в нейтральное положение и работа с тормозами. Если вы не можете включить «нейтралку», не забывайте о том, что необходимо нажимать не только тормоз, но и сцепление, чтобы остановить автомобиль.
Парковка
При парковке автомобиля на механике всегда пользуйтесь ручным тормозом. Вам нужно научиться пользоваться ним каждый раз, когда вы оставляете свою машину, независимо от наклона поверхности. Для дополнительной безопасности рекомендуется оставлять автомобиль на первой передаче.
Если вы припарковались на склоне, переведите рычаг КПП в положение “R”. Не забудьте повернуть передние колеса так, чтобы в случае внезапного начала движения автомобиль не оказался на дороге.
Применяя наши рекомендации, уже через некоторое время переключение передач на механике станет для вас таким же естественным, как дыхание!
Вождение на механике для начинающих: пошаговая инструкция
Выбирая для себя автомобиль, будущие водители становятся перед выбором: какую выбрать марку машины, цвет, тип кузова, а также с механической коробкой передач, либо с АКПП.
Все зависеть будет от личных предпочтений и материальных возможностей. Ведь автомобили с МКПП будут стоить на порядок дешевле, нежели автомат. Но не все знают, как правильно ездить на механике.
Содержание статьи
Для чего нужно умение вождения авто с механической коробкой?
Некоторые автошколы предоставляют такие услуги, как обучение вождению исключительно на автомобили автомат. Это значит, что и права будут выданы соответствующие. То есть, потом сесть за руль МКПП не представится возможным без получения нового удостоверения.
Ситуации в жизни возникают различные, и иногда возникает острая необходимость управлять автомобилем с механической коробкой. Получив права, позволяющие это делать, всегда можно пересесть на автомат. Наоборот же, сделать не получится.
Получив права, позволяющие это делать, всегда можно пересесть на автомат. Наоборот же, сделать не получится.
Покупка авто на механике является более выгодным приобретением. Помимо более низкой цены автомобилей, их эксплуатация выйдет также более экономичной. Как правило, расход топлива у них меньший, и ремонт некоторых деталей выйдет также менее дорогим.
В ситуации, когда оказывается разряженным аккумулятор, можно выйти из положения. Например, перекинуть провода из другого автомобиля для подзарядки. Либо же машина может завестись, с так называемого толкача. Эти варианты не подходят, если транспортное средство с автоматической трансмиссией.
Только используя механическую коробку, можно чувствовать полный контроль над автомобилем. Когда многие манипуляции выполняются на автомате, этого не происходит.
Основы езды на механике
Прежде чем узнать, как научиться ездить на механике, желательно понимать, с чем вообще придется иметь дело:
- Педали.
 При управлении ТС используется три педали: газ (крайняя правая), тормоз (по центру), сцепление (располагается слева). В отличие от автоматической трансмиссии, здесь используются в управлении обе ноги. Если водитель, севший за руль механики новичок, поначалу, это делать будет непривычно.
При управлении ТС используется три педали: газ (крайняя правая), тормоз (по центру), сцепление (располагается слева). В отличие от автоматической трансмиссии, здесь используются в управлении обе ноги. Если водитель, севший за руль механики новичок, поначалу, это делать будет непривычно. - КПП. При помощи смещения шестеренок в трансмиссии, происходит переключение скоростей. На многих автомобилях данный селектор оснащен подсказками, используя которые проще разобраться, какая передача выбрана.
- Тахометр. Располагается на панели приборов, и позволяет определить, сколько коленвал двигателя делает оборотов в минуту. При помощи него новички контролируют, когда необходимо переключаться на следующую передачу.
Разбираемся с передачами на МКПП
Механика тем и отличается от автомата, что требует постоянного контроля водителя, то есть, самостоятельного переключения скоростей. В основном ТС имеют 4 или 5 скоростей, и в дополнении к ним задняя. Чтобы понимать месторасположение каждой, необходимо знать их предназначение.
Коробка передач: инструкция для начинающих
- Всякий раз движение начинается с выжима педали сцепления, таким образом, появляется возможность переходить на другую скорость. Вводить требуемую передачу допустимо в том случае, когда сцепление будет полностью выжато.
- Когда избрана нейтральная передача, при выжимании газа, автомобиль не двинется с места. Когда селектор находится в данной позиции, возможно, выбирать желаемую скорость, включая заднюю.
- Рабочей передачей считается вторая. На ней удобно передвигаться по наклонной местности, а также осуществлять езду в пробках. Первую же обычно используют для старта пути, затем, ускоряясь, переходят на вторую. Набрав еще большую скорость и обороты, можно переходить на третью.
- Труднее освоить неопытным водителям как ездить на механике, на задней передаче. Используя ее, разгон происходит быстрее, нежели на первой, но все же, водить машину часто, таким образом, весьма опасно.
Прежде чем выезжать на автомобиле в город, необходимо хорошо ориентироваться, где какая передача расположена. Теория это хорошо, но в данном случае, необходимы практические навыки. Ведь во время езды отвлекаться и смотреть на селектор, выбирая нужную передачу, нельзя, поскольку это небезопасно. Первое время можно тренироваться на авто, в нерабочем состоянии, доводить до автоматизма включение передач.
Начало движения
Порядок действий:
- Прежде чем, повернуть ключ в замке зажигания, необходимо полностью выжать педаль сцепления левой ногой, а правой нажать на тормоз, и только после этого завести мотор. Мотор заведен, сцепление выжато, можно включать первую передачу (до этого селектор находиться в нейтральном положении). Чтобы автомобиль не заглох, нельзя отпускать левую ногу с педали. Когда машина работает, с тормоза, нога перемещается на педаль газа и одновременно необходимо начинать убирать ногу со сцепления, только плавно.
- Чтобы выполнить переход на следующую скорость, необходимо, чтобы стрелка тахометра приравнивалась к 3000 оборотам.
 Если переключиться слишком рано, то машина может заглохнуть.
Если переключиться слишком рано, то машина может заглохнуть.
Как выполняется переход:
- Правая нога убирается с газа, а левой полностью выжимается сцепление, и в это время селектор переводится в необходимое положение,
- Сцепление необходимо отпустить, а педаль газа нажать,
- Далее в управлении участвует только правая нога, до перехода на следующую скорость или остановки.
Более опытные водители обычно не обращают внимания на показания тахометра, а ориентируются на звук двигателя.
Если автомобиль не разгоняется и слишком низкие обороты, то необходимо переключиться на скорость ниже. А если же обороты слишком высокие, то необходимо включение следующей скорости, чтобы не перегружать двигатель.
Остановка и парковка
Чтобы заглушить автотранспорт можно использовать два варианта:
- Переключение на пониженные передачи, вслед за тем, необходимо выжать педаль тормоза.

- Надавить сцепление и переместить селектор в нейтральную позицию, затем устранить ногу со сцепления и поднажать, если есть надобность, тормоз.
Чтобы износ коробки был меньшим лучше использовать второй способ, и не забывать помимо тормоза обязательно выжимать сцепление.
Припарковав свой автомобиль всегда необходимо использовать ручной тормоз, особенно, если поверхность с наклоном. Также всегда стоит помнить о положении колес во время стоянки. Их требуется выворачивать таким образом, чтобы в случае внезапного движения, машина не очутилась на проезжей части.
Также для большей безопасности советуют переставлять селектор на первую передачу. Это поможет подстраховать авто от случайного скатывания. Но при возобновлении движения, нужно помнить, что селектор требуется переместить в нейтральное состояние. И только потом начинать выжимать сцепление.
На сегодняшний день, некоторые автолюбители новички отдают предпочтение автомобилям с АКПП, считая их более простыми в управлении. Но стоит помнить о том, что механика была и остается наиболее надежной. Наибольший контроль над транспортным средством, увеличенная мощность и экономия в топливе, вознаградят своего владельца за выбор именно МКПП. И приобретя опыт, езда на таких машинах, будет доставлять удовольствие.
Видео инструкция по вождению на МКПП
Внимание!
В связи с частыми изменениями законодательства РФ, информация на сайте не всегда успевает обновляться, поэтому для Вас круглосуточно работают бесплатные эксперты-юристы!
Горячие линии:
Москва: +7 (499) 653-60-72, доб. 206
Санкт-Петербург: +7 (812) 426-14-07, доб. 997
Регионы РФ: +7 (800) 500-27-29, доб. 669.
Заявки принимаются круглосуточно и каждый день. Либо воспользуйтесь онлайн формой.
Как ездить на «механике»?
Как вы знаете, автомобили с механической трансмиссией обычно гораздо дешевле, чем автомобили с автоматическими трансмиссиями. Но кроме экономии на старте и в эксплуатации эта коробка может открыть для вас другие грани вождения автомобиля.
Но кроме экономии на старте и в эксплуатации эта коробка может открыть для вас другие грани вождения автомобиля.
Безусловно, большинство знаковых спортивных автомобилей, как новых, так и легендарных, по-прежнему оснащаются и механикой в том числе. Но даже в случае автомобиля с минимальной мощностью наличие механики может существенно сократить ваш бюджет на обслуживание и эксплуатацию железного коня.
Давайте пройдёмся по некоторым фактам!
Передачи и что это такое
Механика требует от водителя самостоятельно переключать передачи в автомобиле, и, для понимания самого механизма, мы попробуем рассказать о нём вкратце:
-Сцепление
Механизм коробки, который, при нажатии на соответствующую педаль, позволяет вам переключать передачи в произвольном порядке в любое время. Главное, до конца выжимать и отпускать педаль в моменты переключения.
-Нейтраль
При постановке коробки в эту передачу, кстати, никак не обозначенную, крутящий момент никуда не передаётся, и, соответственно, автомобиль не двигается. Если автомобиль стоит «на нейтралке», вы можете включить любую передачу, в том числе и заднюю.
Если автомобиль стоит «на нейтралке», вы можете включить любую передачу, в том числе и заднюю.
Самой популярной передачей для автомобилей, оснащённых механикой и эксплуатирующихся в городских условиях, является, безусловно, вторая. Именно на ней вы будете «толкаться» в пробках, спускаться с горок и держать разрешённую скорость на городских улочках. Да, есть ещё и первая, но, увы, она предназначена только для начала движения по причине своей краткости.
-Задний ход
Задняя передача обладает достаточно большим диапазоном работы, и некоторые автомобилисты утверждают, что даже разгоняться на ней можно очень быстро. Но обычно задние передачи не любят непрерывной эксплуатации, ведь это может привести к поломкам механизма коробки в целом.
Педаль газа, кстати, в условиях механической коробки позволяет на максимум использовать каждую передачу. Можно много говорить о том, что именно на механике вы будете чувствовать каждую передачу, скорость в целом и лучше контролировать машину, но каждый останется при своём мнении, а у нас на сегодня другая цель.
Расположение передач
Самым лучшим способом ускорить своё знакомство с механикой в вашем автомобиле – запомнить порядок движения рычага КПП. Да, на большинстве рычагов нанесена соответствующая маркировка, но она может быть вытерта, да и в движении смотреть не всегда будет получаться. Попробуйте посидеть полчаса без движения, работая лишь рычагом. Да, проверьте как включается задняя передача и не забывайте про педаль сцепления, иначе каждое переключение будет сопровождаться скрежетом или хрустом. Это плохо, и, в дальнейшем, будет стоить определённых денег. Кстати, про переключение: если вы начинающий водитель, попросите опытного товарища прокатить вас на вашем автомобиле и обратите внимание на процесс переключения, скорость, на которой он будет переключаться.
На самом деле, даже если вы запомните с первого раза что и как включается, в голове будет крутиться мысль: «А правильно ли я сделал?». Расслабьтесь – она улетучится из вашей головы с опытом, и со временем вы перестанете обращать на это хоть какой-то процент внимания.
Подбор передачи
Если вы пропустили курс лекций в автошколе, ну или вам про это не рассказывали, ссылаясь на то, что все равно вы купите автомат, давайте пробежимся по этому моменту. Поначалу тут работают всего 2 правила, которые нужно помнить.
Если автомобиль отказывается разгоняться, а обороты двигателя ниже некуда, и автомобиль практически хочет заглохнуть – вы включили слишком высокую передачу. Например – третью вместо первой. Переключитесь ниже.
Если же ситуация обратная, и двигатель буквально кричит – повысьте передачу. И коробку разгрузите, и двигателю отдохнуть дадите.
Если же вы более опытный водитель, и можете переключать глаза от дороги на приборы (а, поверьте, есть и такие товарищи, которым сложно это делать), то смотрите на тахометр. Как только двигатель выходит на 3000 оборотов – переключаемся выше. И наоборот: падаем к тысяче – переключаемся ниже. Ориентироваться по скорости может быть бесполезно, потому как у каждого автомобиля своя скорость переключения. Кому-то достаточно переключаться каждые 25 км/ч, а у кого-то и первая может на 60 заканчиваться. Лучше по-старинке.
Кому-то достаточно переключаться каждые 25 км/ч, а у кого-то и первая может на 60 заканчиваться. Лучше по-старинке.
Запуск
Ну что, про теорию почитали, пора и движение начинать. Лучше всего проверить нейтральную передачу, пошатав рычаг вправо и влево. Убедились? Сцепление в пол и запускаем. Да, это работает даже если автомобиль у вас без ключа. Только с нажатой педалью. А почему? Да потому, что даже если вы оставили автомобиль на передаче и забыли об этом, педаль сцепления спасёт вас от начала движения. Автомобиль запустится, но как только вы педаль отпустите – или поедет или заглохнет. Кстати, зимой лучше подержать педаль после запуска примерно минуту, так масло в коробке быстрее прогреется.
Снова сцепление
Как мы говорили раньше, сцепление – это ваш ассистент при переключении передач, спаситель при запуске двигателя и прочее. Однако помните о том, что с педалью работает только левая нога. Больше эта нога никуда не тянется.
Кстати, я бы не советовал держать сцепление нажатым на светофорах или в пробках. Лучше первое время связка «нейтралка+ручник», потому что педаль действительно тугая, и, в первое время, это может привести к обидному ДТП.
Координация движений
Теперь, поскольку вы уже примерно понимаете как нужно действовать и готовы приоткрыть дверь в мир драйва, ускорений и прочих рекламных слоганов, приземляемся обратно и вспоминаем про координацию и слаженность.
Необходимо ещё раз (да, вы в автошколе прекрасно слышали и выполняли это) прогнать в памяти порядок действий при переключении передач. Выжмите педаль сцепления до конца. Переключите ручку скоростей на первую скорость. Начинайте медленно отпускать педаль сцепления, одновременно с этим плавно и медленно нажимая педаль газа. Нажав педаль сцепления где-то до середины, вы почувствуете, что крутящий момент начал полностью передаваться на колеса. Отпустив плавно педаль сцепления до конца, разгоняйтесь до 25 км/ч. Далее необходимо перейти на вторую передачу. Для этого опять выжмите сцепление до конца и переключите скорость на вторую передачу, после чего плавно, опуская педаль сцепления, медленно прибавляйте газ. Лучше тренировать это почаще, ведь при въезде в горку неправильная работа педалями может привести к откату вашего автомобиля назад, и тогда вы станете сюрпризом для другого автомобилиста. Ну или запаникуете и бросите сцепление. Тогда ваш конь может «укусить» уже впередистоящего. Согласитесь, мало приятного.
Лучше тренировать это почаще, ведь при въезде в горку неправильная работа педалями может привести к откату вашего автомобиля назад, и тогда вы станете сюрпризом для другого автомобилиста. Ну или запаникуете и бросите сцепление. Тогда ваш конь может «укусить» уже впередистоящего. Согласитесь, мало приятного.
Торможение коробкой
Иногда такое понятие называется дауншифтингом и помогает оно не только замедлить автомобиль, но и позволяет вам включить именно ту скорость, которая действительна необходима. Это понятие помогает вам в плохую скользкую погоду, как в летнее время, так и в зимнее, не прибегать к торможению с помощью педали тормоза, в случае, если необходимо снизить скорость, что делает более безопасным передвижение на автомобиле в отличие от машины, оборудованной автоматической трансмиссией.
С точки зрения механики выглядит он так, что торможение, помимо нажатия педали тормоза, осуществляется ещё и переключением передач вниз. Правая нога работает только с педалью тормоза, а левая только со сцеплением, плавно отпуская педаль во избежание резкой передачи крутящего момента.
На самом деле, это только на словах страшно и непонятно. Стоит к этому привыкнуть, и любой автомобиль от архаичного грузовичка до современного спорткара станет вам доступен.
Да, в некоторых моментах механика несколько снижает комфорт вождения, но за это вы будете вознаграждены гораздо большим контролем над автомобилем, повышенной мощностью, лучшей топливной экономичностью, низкой стоимостью обслуживания и недорогим ремонтом (по сравнению с АКПП), ценным жизненным мастерством вождения, которое позволит вам управлять практически любым транспортным средством в мире.
Как правильно ездить на механике?
Привет, друзья! Сегодня я, Евгений Борисов, предлагаю поговорить о вождении автомобиля с механической трансмиссией.
Как часто вы замечали, что на светофоре учебный автомобиль превращается в дикого мустанга: при попытке тронуться просто-напросто глохнет?
Отсутствием плавного старта и большим откатом назад страдают многие новички, но с опытом эта проблема уходит.
Зато приходит понимание, как правильно ездить на механике и как реже посещать автосервисы. Поехали!
Я не волшебник! Я только учусь!
Опытные водители, которые попробовали и механику, и автомат наверняка со мной согласятся – с механической коробкой без опыта ездить сложнее.
Именно поэтому всем, кто только постигает азы вождения, я бы рекомендовал начать обучение именно с нее. После механической коробки вам сам черт не страшен!
Основная сложность для новичков, особенно женского пола, – в невозможности поймать «тот самый момент», когда «сцепление плавно отпускается», а «газ выжимается». И хотя на словах объяснять подобные вещи сложно, попробуем слегка прояснить.
- Еще до начала запуска двигателя, выжмите сцепление до упора левой ногой, а правой – тормоза. Заведите авто, убедившись, что передача выключена (иначе машина может поехать).
- Переведите рычаг переключения КПП (под вашей правой рукой) на 1 скорость. И упаси вас бог, сделать подобное при невыжатом сцеплении.
 После одного раза, может, трагедии и не случится, но при регулярном нарушении правила придется платить за ремонт.
После одного раза, может, трагедии и не случится, но при регулярном нарушении правила придется платить за ремонт. - Переведите правую ногу с тормоза на газ. Плавно отпускайте сцепление и одновременно начинайте утапливать педаль газа. Вы почувствуете, как шестерни трансмиссии «зацепились», а автомобиль «покатился». Следите, чтобы тахометр показывал примерно 2 тыс. оборотов в минуту.
- Не бросайте сцепление резко, иначе заглохните. Делайте всё плавно, словно вы – шаолиньский монах во время медитации.
- При наборе скорости – медленно отпускайте сцепление.
Поспешу приправить инструкцию, от которой вы, вполне возможно, слегка приуныли, порцией позитива: если вы научитесь трогаться с места – считайте, что освоили механику на 80%.
На заметку! Хороший инструктор будет настаивать на четком закреплении ног за той или иной педалью: для сцепления и тормоза – левая, для газа – правая.
Учиться лучше всего на автодроме с ровным покрытием, где вас не будут смущать другие водители (а они, ох, какую нетерпимость проявляют иногда на дорогах).
После того как вы научитесь трогаться, двигаться и останавливаться на площадке, вас «выведут в люди» – предложат прокатиться по городу. Главный совет – не обращайте внимания на недовольные взгляды и «бибиканье».
Просто делайте своё дело, успокаивая себе тем, что рядом инструктор, который, в случае чего, придет на помощь.
Скоростной режим
Сложность с переключением скоростей преодолеть проще, чем научиться плавно трогаться. Как только стрелка тахометра приблизиться к отметке 3 тыс. об/мин:
- отпустите газ, до упора выжмите сцепление и передвиньте рычаг в новое положение (например, на вторую скорость – она, кстати, считается самой рабочей и используется чаще других) – все эти операции делаются синхронно;
- плавно отпускайте сцепление и выжимайте газ (точно так же как вы делали на этапе начала движения).
На заметку! Если во время переключения скорости автомобиль начинает «трясти», то вы поторопились.
Строго говоря, на механике переходить на более низкую передачу перед остановкой машины не нужно, однако в некоторых случаях, например, при движении в пробках, уйти на пониженную передачу целесообразно, чтобы уменьшить расход топлива.
На обледеневших покрытиях зимой и опасных участках также лучше использовать низкие передачи – уходить на них нужно при показаниях тахометра менее тысячи об/мин.
А что делать, если в авто нет тахометра? Инструкторы часто предлагают «слушать» – если мотор «басит», а автомобиль при этом не едет быстрее, то включена слишком высокая передача.
Вот только тем, кто сидит месяц за рулем, очень часто сложно различить «симфонию», поэтому можно ориентироваться на спидометр:
- до 25 км/час – 1-я передача;
- от 25 до 50 – 2-я;
- от 50 до 70 – 3-я.
Смотрите полезные видео уроки, которые я специально подобрал для вас по теме разговора.
Ошибки новичков
Многие начинающие полагают, что намного проще держать сцепление выжатым постоянно, чем ломать голову, когда на педаль нажимать, а когда нет. В этом случае не избежать вам двух зол:
- затекшей левой ноги, которую от постоянного напряжения начнет сводить или «пронзать иголками»;
- преждевременной «смерти» сцепления.
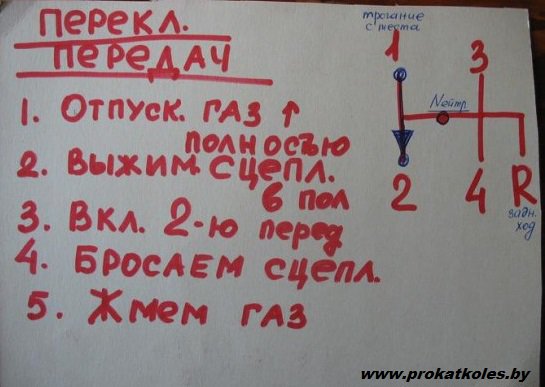
Ногу, конечно, после остановки можно растереть и «привести в чувство», но если вы не хотите ездить исключительно до мастерской, чтобы не сжечь сцепление, убирайте ногу с педали после каждой операции.
Итак, ездить мы научились, но ведь надо еще понять, как останавливаться.
Неопытные водители часто просто сбрасывают скорость, переводят рычаг в нужное положение и жмут на тормоз, хотя такой вариант быстро изнашивает и сцепление, и саму коробку.
Правильный вариант торможения и остановки:
- выжать сцепление;
- перевести рычаг в нейтралку;
- снять ногу со сцепления;
- плавно давить на тормоз до полной остановки.
На заметку! При нейтралке крутящий момент не передается на колеса, это значит, что даже заведенный автомобиль при нейтральной передаче в случае нажатия газа не поедет.
И еще одна распространенная ошибка начинающих – игнорирование ручного тормоза. Использовать ручник нужно каждый раз, когда вы паркуетесь, независимо от угла наклона поверхности.
Дополнительно защитить от «укатывания в бездну» поможет и переведение рычага в положение первой скорости. Если вы остановились на склоне, то выставьте рычаг на «R» и поверните передние колеса.
Повторюсь, можно теоретически вызубрить, как научиться правильно ездить на механике, но без практических навыков и хорошего инструктора, вы даже тронуться с места не сможете. Хотите поспорить?
Поделитесь своими историями практической езды на автомобиле с МКПП – с интересом почитаем. Буду признателен, если поддержите мой блог с помощью репоста статьи в соцсетях. Удачи всем! И до новых встреч!
Этой статьей стоит поделиться
Эффект собаки Павлова: почему учиться водить нужно с МКПП
Новое поколение водителей выбирает «автомат» смело и решительно. Они отбрасывают все предрассудки и главным их требованием к автомобилю становится «автоматичность», на авто любого возраста, мощности и сферы применения. У них миллион аргументов за то, что коробка-автомат это современно, экономично и очень безопасно.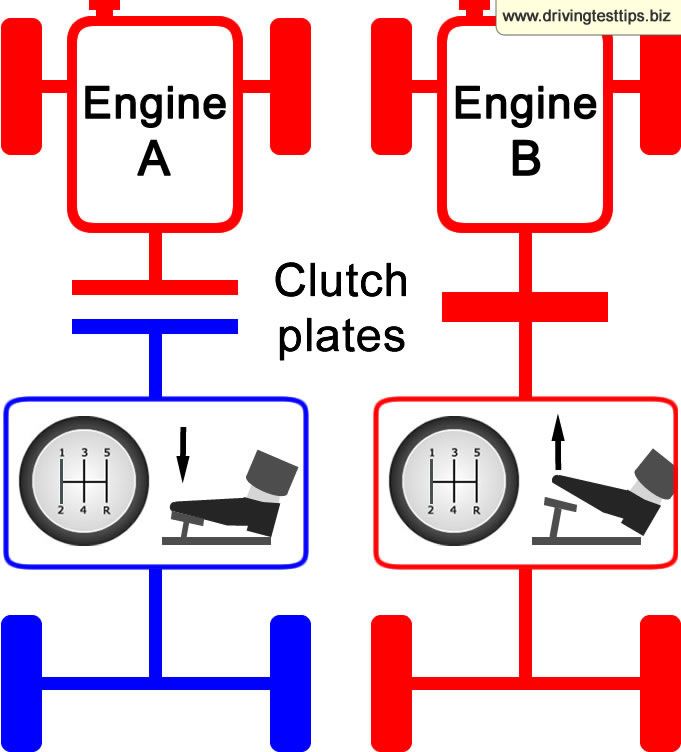 Я в чем-то даже согласен с ними, и даже более чем уверен что для многих таких водителей «автомат» еще и надежнее, чем традиционная МКПП, но все меня все же гложет сомнение: а может, это все просто паника начинающего водителя? Плохая моторика, плохая подготовка и неуверенность в собственных силах?
Я в чем-то даже согласен с ними, и даже более чем уверен что для многих таких водителей «автомат» еще и надежнее, чем традиционная МКПП, но все меня все же гложет сомнение: а может, это все просто паника начинающего водителя? Плохая моторика, плохая подготовка и неуверенность в собственных силах?
И кажется, я нахожу все больше аргументов в пользу того, что первый автомобиль должен быть с механической коробкой передач, а водительские права – без позорной отметки (А) – «строго с автоматической коробкой». И боюсь, что это вовсе не вопрос идеологии, все упирается в простые вещи: безопасность, надежность и… удобство.
Водитель за рулем машины с автоматом, да еще с не самым мощным мотором привыкает работать педалью газа как кнопкой — условно говоря «тяга вкл/тяга выкл». Газ почти в пол со светофора, потом отпустить, потом нажать. Говорить о какой-то управляемости машины, стабильности траектории в повороте, хорошем сцеплении или контроле траектории тягой в этом случае не имеет смысла. Машина на скользком покрытии и в повороте предоставлена сама себе, и хорошо, если есть ESP, он-то и спасет в случае чего.
Машина на скользком покрытии и в повороте предоставлена сама себе, и хорошо, если есть ESP, он-то и спасет в случае чего.
А случаи наступают регулярно, и что называется, «на ровном месте» – в малейшей дуге или легкой колее на автостраде. Совсем дела плохи, когда машинка уже не «стандартный 1,6», а что-то помощнее, ведь не секрет, что многие даже турбированные 1,4 считают несерьезным форматом, переходя с моторов «полтора литра» сразу к какому-нибудь 1,8 TSI.
Водитель на машине с МКПП как минимум в моменты старта и переключений тренирует правую ногу действовать деликатно. Давать столько тяги, сколько нужно для ровного и аккуратного движения. Да и на ходу «механика» требует побольше собранности и аккуратной работы – рывки тяги не гасятся гидротрансформатором и цепью вариатора, их не пытается смягчить умное сцепление преселективного робота. Ошибка водителя тут же приводит к ощутимому последствию в виде неприятного рывка — такой вот «эффект собаки Павлова».
Для того, чтобы научиться, нужна хорошая мотивация, частые повторы и стремление к совершенству. А безнаказанность, которую дают автоматические трансмиссии, расхолаживает, делает ошибки чем-то абстрактным и далеким. Да, на механике ошибка поначалу может привести к более тяжким последствиям, но навык формируется быстрее, чем растет кураж и появляется лихачество. И в повороте «ученый» водитель уже не сбросит резко газ, не «втопит» на скользкой и мокрой колее, не будет дергать дроссель на льду. Буквально за год-два езды с ручной коробкой сформируется устойчивый навык, который может спасти жизни многих людей.
А безнаказанность, которую дают автоматические трансмиссии, расхолаживает, делает ошибки чем-то абстрактным и далеким. Да, на механике ошибка поначалу может привести к более тяжким последствиям, но навык формируется быстрее, чем растет кураж и появляется лихачество. И в повороте «ученый» водитель уже не сбросит резко газ, не «втопит» на скользкой и мокрой колее, не будет дергать дроссель на льду. Буквально за год-два езды с ручной коробкой сформируется устойчивый навык, который может спасти жизни многих людей.
Ладно, безопасность вас не волнует, вы из тех, кто «не превышает» и считает, что ничего и не произойдет, если всегда ездить по ПДД. Это не так, но допустим. Может, вас убедят аргументы из области экономики?
В машине с механической и с автоматической коробкой мотор по сути одинаковый. И управление его тягой совершенно аналогичное. Но вот беда, «автоматчики» действуют педалями заметно жестче, ведь им не надо бояться рывков и ударов, которые типичны для новичков, пытающихся полихачить на МКПП. Динамика разгона, скорее всего, сильно не вырастет, а куда исчезнет «лишняя» энергия мотора? Правильно, в нагрев и износ трансмиссии.
Больше резких движений педалью газа – больше срабатываний блокировки АКПП, больше износ накладок ГДТ, больше износ фрикционов, больше разогрев коробки и больше загрязнений гидроблока. Про бензин я и вспоминать не буду, понятно, что его уйдет больше, даже если вы пытались взять максимально экономичную машину. К нормативному «паспортному» расходу вы не приблизитесь и на километр.
Особо выделю «автоматчиков» с DSG, Powershift и прочими преселективами. Процесс работы такой трансмиссии по сути мало отличается от действий «правильного водителя» с МКПП, разве что переключения под тягой могут быть мгновенными. И попытка действовать противоестественным образом, плохо дозируя мощность и обороты мотора на старте, приводит к резкому износу сцеплений, ударам, рывкам и прочим неприятным последствиям. В отличие от «классических» АКПП коробки типа DSG в таких условиях изнашиваются очень быстро. Для них нужна именно «механическая» манера управления тягой на старте, плавное дозирование газа и добавление после троганья, а попытка старта на холостых или обычный «газ в пол» приведет лишь к раннему визиту в сервис.
Для них нужна именно «механическая» манера управления тягой на старте, плавное дозирование газа и добавление после троганья, а попытка старта на холостых или обычный «газ в пол» приведет лишь к раннему визиту в сервис.
Представьте себе, как пришлось бы действовать педалью сцепления при таких «фокусах». Или плавно-плавно с пробуксовкой пытаться тронуться, особенно в горку это тяжело, или палить сцепление, пытаясь не допустить ударов и пробуксовки колес при старте с «газом в пол».
Что до «страдальцев» с механикой, то они волей-неволей поначалу вынуждены действовать аккуратно. Старт с малых оборотов, и только потом уже мощное ускорение. Если только не игнорировать запах паленого сцепления и удары в трансмиссии, то все будет в порядке, и расходов минимум.
Оптимальный алгоритм, опять же, закрепится буквально через полгода год, причем накрепко. Если же водитель не способен запомнить эти простые вещи, то пара замен комплектов сцепления его немного простимулируют. Это не так дорого, как ремонтировать DSG, но достаточно чувствительно для кармана. «Эффект собаки Павлова» в действии!
«Эффект собаки Павлова» в действии!
Боюсь, если у вас еще не убедил, что начинать нужно на машине с ручной коробкой, то дальше продолжать нет смысла. Хотя… пожалуй, есть еще один аргумент «за».
Наверное, водитель, умеющий ездить на «механике», куда лучше осознает, что там происходит в машине при разгоне и при торможении. А значит, он подготовлен к любым ситуациям. Например, он осознает, что для обгона мотор должен раскрутиться, тогда будет больше тяги, нужно переключить передачу «вниз» и не повышать ее. Для него не будет сюрпризом пауза перед разгоном, которую берет коробка на переключения, он легко поймает ритм переключений в любом режиме движения. А при необходимости вполне успешно подкорректирует автоматический алгоритм для оптимальной работы.
Для водителя, поездившего на «механике», многое в поведении автомобиля становится простым и прозрачным. И ощущение дискомфорта от того, что что-то идет не так, как хотелось бы, отступает. Жить становится чуточку проще, и все, что для этого нужно – сформировать простой навык движения с механической коробкой.
Безусловно, было бы странно ездить на «механике» всю жизнь. Более того, многие современные машины просто не имеют версий с МКПП. Это и не нужно — один раз научившись дозировать тягу и грамотно подбирать передачи для разных дорожных ситуаций, вы будете на полном автоматизме бережно и безопасно «общаться» с АКПП, АМТ, DSG или вариатором. Пожалуй, что ни к чему «механические» навыки только тем, кто выбирает электромобиль, где нет ни ДВС, ни коробки передач. Но золотой век электрокаров все никак не настает. Да и настанет ли?
Опрос
А вы на какой машине учились?
Всего голосов:
Правильный способ настройки вашего автомобиля
ВОССТАНОВЛЕНИЕ АВТОМОБИЛЯ КАК ДО
В то время как многие любители восстановления автомобилей и механики на заднем дворе настраивали свои автомобили на протяжении десятилетий, очень немногие на самом деле делают это правильно. Мы объясним, как
решить эту важнейшую задачу, но сначала мы должны упомянуть одну мелочь:
Мы объясним, как
решить эту важнейшую задачу, но сначала мы должны упомянуть одну мелочь:
Есть ОДНА И ТОЛЬКО ОДНА правильная процедура, которой нужно следовать при настройке автомобиля!
Теперь, когда мы привлекли ваше внимание, давайте начнем заставлять старый фливвер работать должным образом.
Сначала ознакомьтесь с основами
Не приступайте сразу к замене или настройке. Сначала потратьте несколько минут на проверку оборудования. Это важно, так как неправильная работа некоторых систем повлияет на настройку двигателя. Не позволяйте снимать отметку или игнорировать любое из следующего.
- Правильно ли работает система охлаждения? Помимо защиты двигателя от перегрева, работает ли он при надлежащей рабочей температуре? Есть ли утечки? Если есть соединения водяного шланга с пластиной под карбюратором, подключены ли они и работают?
- Аккумулятор полностью заряжен? Генератор / генератор переменного тока работает нормально?
- Топливная система чиста (особенно фильтр) и подкачивается ли под правильным давлением? Есть ли в баллоне свежий бензин?
- Все ли рычаги (воздушная заслонка, акселератор, понижающая передача) двигаются плавно от упора до упора?
- Вся ли проводка в хорошем состоянии? Есть ли обрывы утеплителя? Разъемы заржавели или ослабли?
Теперь мы можем начать
Первое, что нужно сделать при настройке, — это ОСТАВИТЬ ЧЕРТОВЫЙ КАРБЮРАТОР ОДИН! Это последнее, что вы будете настраивать, поэтому не трогайте его. Это приведет к тому, что вам придется «гнаться» за настройками системы зажигания и, возможно, никогда не добиться правильного результата.
Первое правило настройки двигателей — добиться правильной настройки зажигания. Зажигание — это «руководитель группы», а все остальное под капотом — «оркестр», так что не торопитесь, чтобы все исправить.
Вы захотите начать с нового набора точек, конденсатора и заглушек. Провода вилки могут нуждаться или не нуждаться в замене в зависимости от пробега, и мы рекомендуем заменять провода с углеродным сердечником (провода сопротивления) примерно через 15 000 миль на старых автомобилях.Провода с твердым сердечником, как правило, служат намного дольше, но их следует заменять, когда их резиновые заглушки изнашиваются — это предохраняет провода от дугового замыкания на блок цилиндров.
Шаг 1 — Проверните двигатель до верхней мертвой точки, как указано на балансире или шкиве. Откройте крышку распределителя и посмотрите, направлен ли ротор на цилиндр №1 (если нет маркировки, следуйте за проводом свечи к распределителю). Если это 180 градусов от этого положения, проверните двигатель на один оборот до ВМТ.Он должен быть там сейчас. Отметьте линию сбоку от корпуса распределителя и продолжите ее на блоке цилиндров. Это позволит при необходимости перенастроить.
Если это 180 градусов от этого положения, проверните двигатель на один оборот до ВМТ.Он должен быть там сейчас. Отметьте линию сбоку от корпуса распределителя и продолжите ее на блоке цилиндров. Это позволит при необходимости перенастроить.
Причина, по которой вы делаете это, состоит в том, чтобы в дальнейшем предотвратить неправильную замену проводов вилки и облегчить снятие / замену распределителя, если в этом возникнет необходимость. Теперь двигатель механически настроен на работу в правильном порядке.
Шаг 2 — Вытащите старые наконечники, конденсатор и ротор. Проверьте плавность движения пластины подачи вакуума, желательно всасывая вакуумный шланг.Установите новые точки на пластину вместе с конденсатором (на некоторых автомобилях конденсатор крепится к змеевику). Ослабьте прижимной винт распределителя ровно настолько, чтобы позволить движение, и вращайте распределитель, пока рычаг стеклоочистителя на точках не окажется на вершине одного из выступов рабочего кулачка вала. Затяните прижимной винт и отрегулируйте точки для обеспечения надлежащего механического зазора в соответствии с руководством по эксплуатации двигателя. Правильно используйте толщиномер и не торопитесь, потому что вы механически устанавливаете правильный угол остановки *.Установите ротор и крышку.
Затяните прижимной винт и отрегулируйте точки для обеспечения надлежащего механического зазора в соответствии с руководством по эксплуатации двигателя. Правильно используйте толщиномер и не торопитесь, потому что вы механически устанавливаете правильный угол остановки *.Установите ротор и крышку.
* Автомобильные катушки обычно имеют отношение вторичной обмотки к первичной от 200 до 1. Следовательно, входное напряжение 12 В на первичную обмотку катушки приведет к выходному напряжению 24 000 В на вторичной обмотке. Вот где свечи зажигания получают электричество. Индуктивность — это не вечный двигатель и не «свободная энергия». Есть много «однако» и других соображений, о которых нужно беспокоиться. Самая большая из них — это неспособность катушки удерживать наведенное напряжение после того, как оно нарастает.Через очень короткое время напряжение исчезнет, что приведет к слабой искре. Кроме того, для накопления заряда катушке требуется определенное количество времени. Это время задержки , обычно определяемое как угол поворота распределительного вала на градусов, в течение которого точки закрываются. Слишком мало времени ожидания, и катушка не успевает полностью зарядиться. Слишком большое время ожидания, и с катушки произошел сброс заряда, в результате чего возникла слабая искра. Колебания, низкое энергопотребление, пропуски зажигания, пинг и ряд других состояний являются симптомами неправильной задержки.
Слишком мало времени ожидания, и катушка не успевает полностью зарядиться. Слишком большое время ожидания, и с катушки произошел сброс заряда, в результате чего возникла слабая искра. Колебания, низкое энергопотребление, пропуски зажигания, пинг и ряд других состояний являются симптомами неправильной задержки.
Шаг 3 — Закройте новые заглушки и установите их, стараясь не затягивать резьбу в блоке слишком сильно. Наденьте на них провода вилки, соблюдая порядок зажигания. Убедитесь, что провода вставлены в крышку распределителя и катушку.
Шаг 4 — Достаньте измеритель выдержки и подключите его. Красный провод идет к точечной стороне катушки (отрицательный вывод), а черный зажим фиксируется на любой хорошей точке заземления на двигателе. Запустите двигатель и измерьте угол остановки.Если он не находится в середине допустимого диапазона (скажем, 24 градуса, когда диапазон составляет 20-26 градусов), остановите двигатель и переместите зазор между точками ближе, чтобы поднять стойку, или дальше, чтобы опустить ее. Продолжайте делать это до тех пор, пока задержка не станет правильной. Угол задержки всегда устанавливался путем правильной регулировки зазора в точке воспламенения. Разрыв точек вашего автомобиля был рассчитан инженерами для приблизительного определения угла остановки, но отдельные наборы точек могут значительно различаться по своим механическим и электрическим характеристикам. Единственный способ правильно установить точки воспламенения — использовать измеритель выдержки.
Шаг 5 — Достаньте лампу газораспределения, — наиболее часто используемый инструмент для обслуживания двигателя. Почему злоупотребляют? Ну, потому что внутренние компоненты двигателя со временем изнашиваются лишь в минимальных количествах, а это означает, что цепи или шестерни ГРМ не «прыгают» и не расшатываются между настройками. Причина изменения фаз газораспределения двигателя заключается в том, что угол остановки изменяется по мере износа дворников на остриях.
Почему? Поскольку задержка измеряется вращением распределительного вала, а частота вращения распредвала вдвое превышает скорость коленчатого вала, на каждые два градуса задержки зажигание отключается от правильной настройки, синхронизация двигателя будет отклоняться на один градус! Если при периодической проверке двигателя необходимо изменить время, это означает, что точки изношены (тем самым увеличивая время простоя). Цепь ГРМ не проскочила, как многие считают. И наоборот, если вы правильно установите точки при каждой настройке, вы обнаружите, что время никогда не меняется!
Шаг 6 — Установите синхронизацию, подключив свет (индуктивный или прямой), а затем отметьте правильное положение синхронизации на шкиве кривошипа или демпфере. Следуйте инструкциям по эксплуатации двигателя и сделайте легко читаемую отметку с помощью белого цвета (жидкая бумага) или мелка. Отсоедините вакуумную линию от распределителя и воткните в нее карандаш или гвоздь, чтобы предотвратить утечку вакуума.Запустите двигатель и дайте ему поработать со скоростью 500-600 об / мин, чтобы предотвратить любое действие центробежного механизма продвижения (если он есть), а затем медленно вращайте распределитель, пока метка синхронизации не совпадет с его указателем. Затяните прижим распределителя. Если двигатель не работает достаточно медленно, снова включите рычаг акселератора на карбюраторе. Если двигатель работает слишком медленно, увеличьте обороты холостого хода. Еще раз проверьте время и затем погасите свет.
Еще раз проверьте время и затем погасите свет.
Шаг 7 — Теперь (НАКОНЕЦ!) Можно регулировать карбюратор.Во-первых, вы хотите отрегулировать винт смеси холостого хода (или винты, если у вас 2- или 4-цилиндровый карбюратор). Когда двигатель прогрет до правильной рабочей температуры (это важно, подождите, пока он прогреется!), Медленно поверните один винт по часовой стрелке, пока двигатель не начнет спотыкаться или работать с неровностями, затем поверните его примерно на один оборот. Отрегулируйте другой винт таким же образом, пока двигатель не будет работать плавно.
Теперь установите обороты холостого хода двигателя в соответствии с инструкциями по эксплуатации или личными предпочтениями (нам нравится немного более высокие обороты холостого хода, около 800-900, но делайте то, что вам нравится).Отрегулируйте винты смеси холостого хода, если двигатель работает немного грубо.
Шаг 8 — Управляйте автомобилем и обращайте внимание на любые неровности, колебания или пропуски зажигания. Он должен работать отлично, но в противном случае вам придется диагностировать проблему. Если это не что-то вроде ослабленного провода свечи (ой!) Или что-то еще очевидное, это могут быть неисправные системы карбюратора, недостаточная компрессия и т. Д., Но, по крайней мере, вы будете знать, что системы зажигания и холостого хода настроены правильно.
Он должен работать отлично, но в противном случае вам придется диагностировать проблему. Если это не что-то вроде ослабленного провода свечи (ой!) Или что-то еще очевидное, это могут быть неисправные системы карбюратора, недостаточная компрессия и т. Д., Но, по крайней мере, вы будете знать, что системы зажигания и холостого хода настроены правильно.
data-matched-content-ui-type = «image_card_stacked» data-matched-content-rows-num = «3» data-matched-content-columns-num = «1» data-ad-format = «autorelaxed»>
Симметрия времени пребывания в случайных блужданиях и молекулярных двигателях
Biophys J.1 июня 2007 г .; 92 (11): 3804–3816.
Департамент теоретической физики Королевского технологического института (KTH), Стокгольм, Швеция
Поступила в редакцию 13 декабря 2006 г .; Принято 1 февраля 2007 г.
Эта статья цитировалась в других статьях в PMC.Abstract
Статистика шагов и времени пребывания в обратимых молекулярных моторах отличается от статистики завершения цикла в кинетике ферментов. Причина в том, что ступень — это лишь один из нескольких переходов в механохимическом цикле. В результате теоретические результаты о завершении цикла в кинетике ферментов не применимы к данным по шагам.Чтобы обеспечить правильную оценку параметров и направить анализ данных и планирование экспериментов, необходима теоретическая обработка, которая учитывает это наблюдение. В этой статье мы моделируем распределение времени ожидания и количества шагов вперед и назад, используя процессы первого прохода, исходя из предположения, что шаги вперед и назад соответствуют разным направлениям одного и того же перехода. Мы расширяем последние результаты для систем с одним циклом и рассматриваем полное распределение времени пребывания, а также модели с несколькими путями, обнаруживаемыми подшагами и отсоединениями.Наши основные результаты — это соотношение симметрии для распределений времени простоя в реверсивных двигателях и соотношение между некоторыми относительными частотами шагов и свободной энергией за цикл.
Причина в том, что ступень — это лишь один из нескольких переходов в механохимическом цикле. В результате теоретические результаты о завершении цикла в кинетике ферментов не применимы к данным по шагам.Чтобы обеспечить правильную оценку параметров и направить анализ данных и планирование экспериментов, необходима теоретическая обработка, которая учитывает это наблюдение. В этой статье мы моделируем распределение времени ожидания и количества шагов вперед и назад, используя процессы первого прохода, исходя из предположения, что шаги вперед и назад соответствуют разным направлениям одного и того же перехода. Мы расширяем последние результаты для систем с одним циклом и рассматриваем полное распределение времени пребывания, а также модели с несколькими путями, обнаруживаемыми подшагами и отсоединениями.Наши основные результаты — это соотношение симметрии для распределений времени простоя в реверсивных двигателях и соотношение между некоторыми относительными частотами шагов и свободной энергией за цикл. Мы демонстрируем наши результаты, анализируя недавние данные о шагах для бактериального жгутикового мотора, и обсуждаем последствия для эффективности и обратимости субъединиц, генерирующих силу.
ВВЕДЕНИЕ
Прогресс в методах работы с отдельными молекулами позволил наблюдать отдельные стадии во многих моторных белках и точно измерять распределение времени пребывания, т.е.е., периоды небольшого движения или его отсутствия между шагами. Примерами являются прямые и обратные этапы процессных молекулярных моторов, таких как кинезин (1–4), миозин V (5–8), цитоплазматический динеин (9) или РНК-полимераза (10), а также ступенчатые вращения АТФ-синтазы (11–17). ) и жгутиковый мотор (18). Наблюдения за ступенями и распределением времени пребывания предлагают путь к пониманию микроскопического механизма и детального движения таких систем, помимо того, что доступно только через знание средней скорости оборота.
Время пребывания — это примеры времен первого прохождения, которые широко изучались в теории случайных блужданий (19). Таким образом, важным этапом моделирования является формулировка проблемы первого прохода, описывающей экспериментальную ситуацию. Тщательное изучение траекторий шагов с высоким временным разрешением на основе нескольких моторных белков (1–9,11–18) показывает, что шаги являются очень быстрыми событиями по сравнению с типичным временем пребывания. Поэтому в описании дискретного состояния разумно идентифицировать шаг с одним переходом, а направление шага — с направлением этого перехода (20, 21).Идентификация шагов с одиночными переходами естественно следует из предположения, что каждое состояние имеет четко определенное среднее положение, и является основным предположением в этой статье.
Таким образом, важным этапом моделирования является формулировка проблемы первого прохода, описывающей экспериментальную ситуацию. Тщательное изучение траекторий шагов с высоким временным разрешением на основе нескольких моторных белков (1–9,11–18) показывает, что шаги являются очень быстрыми событиями по сравнению с типичным временем пребывания. Поэтому в описании дискретного состояния разумно идентифицировать шаг с одним переходом, а направление шага — с направлением этого перехода (20, 21).Идентификация шагов с одиночными переходами естественно следует из предположения, что каждое состояние имеет четко определенное среднее положение, и является основным предположением в этой статье.
Моторные белки являются циклическими ферментами, но вопреки более ранним предположениям (22,23), этапы и время ожидания, полученные во многих экспериментах с одной молекулой, недостаточно хорошо описаны с точки зрения завершений цикла в кинетике ферментов. Это недавно было продемонстрировано на моделях, в которых один цикл учитывает как шаги вперед, так и назад (20). В этом случае среднее количество шагов вперед и назад отличается от среднего количества завершенных циклов вперед и назад, а среднее время задержки между шагами отличается от среднего времени завершения цикла. Различия могут быть значительными даже в условиях, когда обратных шагов почти не происходит. Основная причина этого различия заключается в том, что двигатель с одним или несколькими промежуточными состояниями за цикл находится в другом состоянии сразу после шагов вперед и назад. Следовательно, экспериментальная траектория шагов вперед и назад не дает явной информации о завершенных циклах вперед и назад.
В этом случае среднее количество шагов вперед и назад отличается от среднего количества завершенных циклов вперед и назад, а среднее время задержки между шагами отличается от среднего времени завершения цикла. Различия могут быть значительными даже в условиях, когда обратных шагов почти не происходит. Основная причина этого различия заключается в том, что двигатель с одним или несколькими промежуточными состояниями за цикл находится в другом состоянии сразу после шагов вперед и назад. Следовательно, экспериментальная траектория шагов вперед и назад не дает явной информации о завершенных циклах вперед и назад.
Различные состояния, полученные сразу после шагов вперед и назад, также подразумевают, что последовательные направления шагов коррелированы (20). Этот прогноз будет подтвержден в следующем разделе, где мы проанализируем данные о шагах от Sowa et al. (18) для жгутикового двигателя и найдите четкие ступенчатые корреляции, показанные на рис. Напротив, последовательные завершения цикла статистически независимы (24,25).
Анализ данных шагания по траектории A . ( a ) Данные шага и результат обнаружения шага (, линия лестницы ).Линии сетки указывают теоретическую длину шага d = 13,8 °. Шаг соответствует теоретической длине шага в интервалах, прерываемых событиями дрейфа ( стрелки, ), а соседние интервалы не совпадают по фазе друг с другом. ( b ) Шаг-ступенчатая автокорреляционная функция, как определено в формуле. 15. Измеренная корреляционная функция ( квадратов ) согласуется с теоретическим предсказанием ( кружков ) с использованием условных вероятностей разделения от.Символы того же размера, что и ориентировочные планки погрешностей. ( c ) Функции распределения P ± ( t ) для четырех различных времен выдержки. Все планки ошибок показывают стандартные отклонения от оценок начальной загрузки.
Наблюдение за тем, что шаги коррелированы, имеет важное значение для интерпретации пошаговых экспериментов, а также мотивирует дальнейшее теоретическое изучение статистики шага, выходящее за рамки предположения (26–28) о независимых шагах и временах задержки.В этой статье мы расширяем теорию Цыганкова и др. (20) двумя способами. Во-первых, мы рассматриваем распределения условных времен пребывания вместо средних значений. Во-вторых, мы рассматриваем более широкий класс моделей, включая моторные отслоения, подшаги и множественные пути.
Наши основные результаты — это симметрия распределения для условных времен задержки и простое соотношение между рассеиваемой свободной энергией за цикл, Δ G , и некоторыми вероятностями условного шага. Для большого количества моделей, относящихся к описанию обратимых моторных белков, мы получаем
(1a)
(1b)
Здесь ρ ++ ( t ) и ρ −− ( t ) — функции плотности вероятности для условного времени ожидания между двумя последовательными шагами вперед и назад соответственно, — соответствующие интегрированные функции вероятности, π ++ — вероятность того, что за шагом вперед следует другой шаг вперед, и π −− , что за шагом назад следует другой шаг назад.Различные типы времени пребывания показаны на рис. 1 просто означает, что условные времена выдержки τ ++ и τ −− являются случайными величинами с равным распределением. Однако уравнение. 1 ничего не говорится о распределении времени пребывания между ступенями разного направления, которые в целом имеют разное распределение.
Пример четырех различных условных времен выдержки в модели с одним шагом на ферментативный цикл (синтетические данные).Координата x ( t ) может быть положением линейного двигателя, чистым вращением вращающегося двигателя или чистым количеством субстрата или продукта в ферментативной реакции, и изменяется ступенчато с шагом d . Линия лестницы представляет собой идеализированную скользящую среднюю.
Уравнение 1 справедливо и при конечной средней скорости. Например, двигающийся вперед двигатель будет делать в основном шаги вперед, но в конечном итоге может сделать два последовательных шага назад. Время ожидания между такими парами шагов ++ и −− имеет одинаковое распределение, хотя вероятность наблюдения двух последовательных шагов назад может быть очень мала для двигателя с сильным прямым смещением.
На практике необходимость наблюдать значительное количество событий ++ и −− для проверки или применения уравнения. 1 может быть экспериментальной задачей. Например, двигатели, управляемые АТФ, такие как кинезин или миозин V, обычно имеют Δ G ATP ≈ −25 k B T in vivo (29). Это означает, что −− события очень редки (см. Уравнение 18), если не приложена внешняя нагрузка (1–8).
Чтобы извлечь качественную информацию из экспериментального теста симметрии времени пребывания, необходимо характеризовать класс моделей, которые удовлетворяют уравнению.1. Мы пытаемся сформулировать общую характеристику этого класса. Это означает, что некоторые модели в рамках этой характеристики не будут реалистичными описаниями биологических систем. С другой стороны, большое количество моделей-кандидатов может быть исключено, если в какой-либо системе не соблюдается симметрия времени пребывания. Мы находим два достаточных предположения для уравнения. 1 для удержания, что мы называем сильной связью и свойством узкого места. В рамках модели дискретного состояния, которую мы используем, эти предположения легко сформулировать, но от них также можно отказаться (30).
Свойство узкого места является предположением о топологии модели. Это означает, что шаги вперед и назад соответствуют переходам в одно состояние или из него в механохимическом цикле, которое мы называем состоянием узкого места. Это гарантирует, что состояние системы однозначно определяется после каждого наблюдаемого шага, независимо от направлений предыдущего шага. Одно только свойство узкого места приводит к особенно простой форме для ступенчатых корреляций, представленных в формуле. 15, что можно проверить экспериментально.
Предположение о сильной связи, математически определенное в формуле. 20, связано с микроскопической обратимостью. Физически это означает, что в механохимическом цикле нет бесполезной диссипации свободной энергии. В дополнение к тесной связи в обычном смысле (30), т. Е. Взаимно однозначному соответствию между расходом топлива и шагами вперед, оно включает предположение, что шаги назад тесно связаны с синтезом топлива. В результате двигатели с сильной связью фактически являются одномерными системами в том смысле, что только одна координата реакции, т.е.г., положение, необходимо для описания их работы.
Сильная муфта не обязательно подходит для всех двигателей. Например, прямые ступени миозина V тесно связаны с гидролизом АТФ, тогда как недавно сообщалось о обратных ступенях, не зависящих от связывания АТФ (8). Другой пример — кинезин, для которого сообщалось о связывании АТФ во время шагов в обоих направлениях (1,2). С другой стороны, сильная связь может быть возможна в некоторых роторных двигателях, по крайней мере, при определенных условиях (16,30–32).
В нескольких недавних работах (33–36) используются скрытые марковские модели для оценки кинетических параметров непосредственно из экспериментальных траекторий и, таким образом, в принципе используется вся информация в данных и обходятся трудности, связанные с обнаружением ступенек. Однако этот подход не отменяет необходимости теоретического понимания возможностей и ограничений лежащих в основе стохастических моделей. Наши результаты должны служить полезным руководством при применении этих методов.
Уравнение 1 соответствует аналогичному результату в кинетике цикла (23–25,37).Используя символ «∼» для обозначения свойств времени цикла, мы получаем
(2)
где — функции плотности вероятности для времени ожидания перед прямым (+) или обратным (-) завершением цикла, — это относительные частоты завершенных прямых и обратные циклы соответственно, и являются потоками одностороннего цикла (37). Уравнение 2 основано на тех же предположениях, что и уравнение. 1 (24,25). Однако время ожидания в формуле. 2 не описывают экспериментальные времена пребывания, наблюдаемые в шаговых экспериментах на моторных белках (20).Различие между временем завершения цикла и временем ожидания приводит к значительным различиям при моделировании и интерпретации данных пошагового управления.
Одним из примеров такого различия является возможность вычислить Δ G из наблюдений за шагами вперед и назад. В этом случае, используя результат завершения цикла в формуле. 2 по шаговым данным может дать большие систематические ошибки в оценке Δ G , которых можно избежать, если уравнение. Вместо этого используется 1.
Родственный пример касается того, как интерпретировать соотношение наблюдаемых шагов вперед и назад, которое было измерено для кинезина в диапазоне сил и концентраций АТФ (1–3).Силовую зависимость этого отношения можно описать как примерно пропорциональную exp (- cF x d / k B T ), где d = 8,2 нм — длина шага, F x — приложенная нагрузка, а c — числовой коэффициент, значительно меньший единицы. Рассеиваемая свободная энергия за цикл зависит от приложенной нагрузки как
(3)
Это означает, что уравнение. 2 предсказывает c = 1, если предполагается, что шаги соответствуют завершенным циклам.В отличие от уравнения. 1 не дает никаких оснований даже ожидать экспоненциального поведения соотношения шагов вперед и назад (20) и предполагает, что π ++ / π −− является более подходящей величиной для изучения. Как упоминалось выше, кинезин может не удовлетворять сильному сцеплению, и в этом случае нужно смотреть на более сложные модели. В любом случае четкое различие между этапами и завершенными циклами важно для правильной интерпретации экспериментов.
Остальная часть статьи организована следующим образом. В следующем разделе мы сделаем набросок вывода наших результатов для моделей, изученных Цыганковым и его коллегами (20) и Цианом (21). Мы также обсуждаем ступенчатые корреляции. После этого мы обобщаем наши результаты на более широкий класс моделей и обсуждаем отслоения и множественные пути в механохимическом цикле. Мы также обобщаем уравнение. 1 для случая нескольких обнаруживаемых подшагов. Чтобы проиллюстрировать наши результаты, мы затем проанализируем данные о шагах для жгутикового мотора перед заключительным обсуждением.Подробные выводы приведены в Приложениях.
ПОСЛЕДОВАТЕЛЬНЫЕ МОДЕЛИ
В этом разделе мы выводим уравнение. 1 и некоторые связанные результаты в простейшем случае — последовательной модели.
Рассмотрим модель с одним циклом, состоящим из последовательности N состояний (см.), Где мы определили [ k ] l для обозначения состояния k в цикле l , связанном с позицией ld . Это основная модель кинетики ферментов (24,37), которая использовалась для описания моторных белков, таких как кинезин (23,38,39), миозин V (22) и F 1 -АТФаза (40).По конструкции он удовлетворяет как сильной связи, так и свойству узкого места.
Простая последовательная модель фермента или моторного белка с N состояниями за цикл, [0] l , [2] l ,…, [ N — 1] l . Модель можно рассматривать как смещенное случайное блуждание по периодической решетке состояний. Цифры в скобках обозначают разные состояния и обозначают разные циклы. Состояние [ k ] l обозначает такое же структурное состояние, как [ k + N ] l ≡ [ k ] l + 1 , но с позиционной или угловой ориентацией x (для линейный и роторный двигатели соответственно) смещены на длину шага d .Стрелки указывают разрешенные переходы между соседними состояниями со скоростью перехода u j , w j . Жирные сплошные стрелки обозначают основные конформационные изменения, которые приводят к наблюдаемым ступеням, подобным тем, что в. Остальные переходы обозначены пунктирными стрелками. В моторном белке такими переходами могут быть, например, связывание или высвобождение лигандов или небольшие конформационные изменения, которые скрыты в экспериментальном шуме.
Мы обозначаем скорость прямого (обратного) перехода из состояния j в соседние состояния как u j ( w j ), как указано в.Скорости перехода являются положительными и периодическими, т. Е. u j + N = u j , w j + N = w j , и, возможно, функции внешних нагрузок и концентраций. различных видов в окружающем растворе. Для целей этого обсуждения предполагается, что скорости являются произвольными положительными константами, некоторые из которых могут быть настроены экспериментально.
Мы предполагаем, что переходы между разными циклами производят наблюдаемые шаги вперед (+) или назад (-).Если модель описывает фермент, наблюдаемым этапом может быть высвобождение или поглощение продукта или молекулы субстрата.
Подсчет шагов отличается от подсчета завершений цикла, что можно проиллюстрировать с помощью следующего мысленного эксперимента. Рассмотрим последовательную модель с N = 2 состояния за цикл и траекторией, по которой двигатель проходит через состояния. Это завершает один прямой цикл от [0] 0 до [0] 1 , но производит три шага: один назад ([0] → [1] −1 ), затем два вперед ([0] −1 → [0] 0 и [1] 0 → [0] 1 ).Из-за таких событий ни количество шагов, ни время задержки между шагами не описываются точно в терминах завершения цикла. Требуется другое лечение.
Временная эволюция системы — это случайное блуждание по периодической одномерной решетке состояний, где средняя скорость может быть отличной от нуля. Чтобы упростить обозначение, мы теперь используем j для обозначения состояния в любом цикле с условием, что j и j + N являются эквивалентными состояниями в разных положениях.
Вероятность q j ( t ) находиться в состоянии j в момент времени t развивается в соответствии с Основным уравнением (19), в данном случае
(4)
State j имеет свободную энергию G j , и согласно подробному балансу, разница свободной энергии между двумя соседними состояниями связана со скоростью перехода через периодичность скоростей, мы находим
(5)
Направление среднего дрейфа положительно (на вправо на дюймов), если рассеиваемая свободная энергия за цикл, Δ G , отрицательна, и равна нулю, если Δ G = 0 (37,41).
Отслеживание положения производит серию шагов вперед (+) и назад (-), разделенных случайным временем задержки, как показано на рисунке. Наша цель — описать статистику такой траектории, т.е. флуктуации времени пребывания и количества шагов вперед и назад, которые затем можно будет сравнить с экспериментальными данными.
Вслед за Цыганковым и др. (20) вводим вероятности попарного расщепления π ++ , π + — , π — + и π −− , где π ++ и π + — — вероятность того, что за шагом вперед следует шаг вперед или шаг назад, соответственно, и аналогично для π ++ , π −− .Вероятности расщепления удовлетворяют
(6)
Аналогичным образом вводятся случайные величины τ ++ , τ + — , τ — + и τ −− для условное время задержки, где τ ++ — время задержки между двумя последовательными шагами вперед и так далее, как показано на. После того, как правильная задача первого прохода для описания времени пребывания была сформулирована, явные выражения для вероятностей расщепления и среднего условного времени пребывания могут быть вычислены для произвольных N (20), используя стандартные методы (19).
ПРОБЛЕМА ПЕРВОГО ПРОХОДА
Теперь мы опишем проблему первого прохода для времен пребывания в последовательных моделях, которую мы затем используем для вывода уравнения. 1. Симметрия времени выдержки обусловлена взаимно-однозначным отображением между каждым −− событием, то есть двумя последовательными шагами назад и временем выдержки между ними, и соответствующим ++ событием. Это ключевое наблюдение для обобщения уравнения. 1 к более сложным моделям в следующих разделах.
Мы моделируем вероятности расщепления и функции распределения вероятностей для времен пребывания как первую задачу выхода из интервала состояний 0, 1,…, N — 1.Одним из способов решения этой проблемы является подход с поглощающими границами (19), который означает решение сокращенного главного уравнения для состояний 0, 1,…, N — 1 с поглощающими границами на обоих концах (20,21). Из предположения, что шаги создаются переходом, следует, что сразу после шага + система находится в состоянии 0 (± lN ), а сразу после шага — в состоянии N — 1. (± лН ).
Запишем сокращенное Основное уравнение в матричной форме, где матрица M имеет элементы
(7)
и 0 ≤ i , j ≤ N — 1.Элемент M ij — это скорость перехода из состояния j в состояние i . Функции вероятности задаются исходящим током вероятности,
(8)
(9)
, где ± указывает начальное состояние q j (0), заданное направлением предыдущего шага (см. Уравнение 39). Нормализация распределений требует, чтобы
(10)
СИММЕТРИЯ ВРЕМЕНИ ЗАДЕРЖКИ
Чтобы получить уравнение.1, мы показываем, что ряды Тейлора π ++ P ++ ( t ) и π −− P −− ( t ) идентичны до фактора, от которого уравнение. 1 следует. Фактический расчет приведен в Приложении А, и теперь мы обсудим некоторые его последствия.
Во-первых, интересно отметить, что периодичность модели не является необходимой для симметрии времени пребывания, только чтобы получить простую связь между π ++ , π −− и Δ G в формуле.1b.
Во-вторых, распределение вероятностей ++ / −− имеет простую замкнутую форму для (периодических) последовательных моделей. Как показано в Приложении B,
(11)
, где λ j — собственные значения матрицы M . Это распределение суммы N независимых экспоненциальных случайных величин со средними значениями
Явные выражения для всех четырех условных распределений времени задержки для случая N = 3 даны Qian (21).Как и ожидалось из расчетов в Приложении B, не существует простой связи между ρ + — ( т ) и ρ — + ( т ).
Уравнение 12 действительно только в том случае, если собственные значения λ j различны. Это общая ситуация, поскольку нет никаких симметрий или других причин ожидать вырождений. Однако уравнение. 1 справедливо и в вырожденном случае.
Наконец, стоит отметить, что последовательные модели в этом разделе также могут быть получены как дискретизация сверхзатухающей одномерной диффузии (42) в произвольном потенциале U ( x ) между двумя точками A и В (см.).В этом случае наши результаты означают, что время ожидания между последним касанием на A и первым касанием на B и обратное время ожидания между последним касанием на B и первым касанием на A имеют одинаковое распределение. Эта пара проблем первого прохождения ранее изучалась Биром и др. (43).
Уравнения движения частицы ( заштрихованный кружок ), диффундирующей в произвольном потенциале ( сплошная кривая ), могут быть дискретизированы в последовательную модель (42).В континуальном пределе симметрия времени пребывания для дискретизации преобразуется в равные распределения для двух времен ожидания первого касания последнего касания между (произвольными) позициями A и B .
Направления шагов как цепь Маркова
Тот факт, что двигатель находится в другом состоянии сразу после шагов в разных направлениях, означает, что направления шагов могут быть коррелированы. В этом разделе мы сформулируем это наблюдение математически и укажем на некоторые экспериментально важные следствия.
Пусть π + ( k ) и π — ( k ) = 1 — π + ( k ) будут вероятностями, что шаг k траектория — шаг вперед или назад соответственно. В простейшем случае отсутствия подшагов или отделений определения вероятностей попарного расщепления дают
(12)
Уравнение 12 описывает последовательность шагов вперед и назад как цепь Маркова (19,20), а ограничения нормализации в Уравнение6 оставляет два независимых параметра в матрице перехода 2 × 2.
Средние частоты π ± * шагов вперед и назад были измерены для нескольких моторных белков (1,2,5,9). В нашей модели эти частоты задаются стационарным распределением уравнения. 12 (20),
(13)
В отличие от отношения количества прямых и обратных циклов в уравнении. 2, отношение π + * / π — * шагов вперед и назад, как правило, не равно exp (- Δ G / k B T ).Оглядываясь назад на уравнение. 3, мы не видим общих причин ожидать, что соотношение шагов вперед и назад будет экспоненциально зависеть от приложенной нагрузки.
Несколько экспериментов разделили время пребывания в соответствии с направлением следующего шага (1–3). Наша модель дает функции плотности вероятности прямого и обратного времени пребывания как
(14)
Так как ρ + — ( t ) и ρ — + ( t ) в общем случае не являются связанных простым способом, не следует ожидать равных времен ожидания перед шагами вперед и назад, в отличие от случая времени завершения прямого и обратного цикла (23–25).
Уравнение 12 подразумевает, что направления шага коррелированы, и дает функцию корреляции шаг-шаг
(15)
, где с м = ± 1 указывает направление шага м и
(16 )
— собственное значение матрицы перехода в уравнении. 12 (20). Другое собственное значение 1.
Обратите внимание, что | γ | <1, поскольку π ± ± <1. Кроме того, разумно ожидать π ++ ≤ π — + , поскольку шаг вперед, следующий за шагом назад, может быть выполнен с помощью один переход, в то время как весь цикл должен быть пройден, прежде чем за шагом вперед последует другой шаг вперед.Подставив π ++ ≤ π — + в уравнение. 16, и используя нормировку в формуле. 7, получаем
(17)
По-видимому, следует ожидать отрицательно коррелированных шагов, −1 < γ ≤ 0. Некоррелированные шаги ( γ = 0) возникают в системах с N = 1, т. Е. простые случайные блуждания, а также некоторые частные случаи расширенных моделей в следующем разделе.
Верхняя граница числа n −− −− событий полезна для оценки режима, в котором наши результаты могут быть применены на практике.Грубая оценка дается как
(18)
Следовательно, количество шагов от n до , необходимых для получения адекватной статистики, растет, по крайней мере, экспоненциально с уменьшением Δ G .
РАСШИРЕННЫЕ МОДЕЛИ
Помимо простейших описаний в терминах последовательной модели для доминирующего пути (если он есть), возможны более сложные ситуации с множественными путями (5,44–48). Общее (крупнозернистое) описание моторного белка будет отслеживать как положение, так и потребление молекул топлива, что требует, чтобы модель включала эффективную химическую координату в дополнение к положению мотора (30).Справедливы ли свойства симметрии времени пребывания последовательных моделей для более общих случаев? Как мы увидим дальше, ответ — «да» для большого класса моделей, в которых движение по-прежнему является одномерным.
С помощью расширенных моделей мы ищем общие свойства, которые подразумевают симметрию времени пребывания, даже если не все модели с этими свойствами являются биологически релевантными. Мы находим, что предположений о сильной связи и узких местах, упомянутых во введении, достаточно.Это означает, что если наблюдается несоблюдение симметрии времени пребывания для конкретной системы, то можно сделать вывод, что свойства сильной связи или узкого места отсутствуют. Чтобы смоделировать такую систему, необходимо выйти за рамки представленных ниже расширенных моделей, например, в соответствии с тем, что обсуждали Бустаманте и его коллеги, Рейманн и Юлихер и его коллеги (30, 49, 50). Особая ситуация без сильной связи, но со свойством узкого места проиллюстрирована ниже на примере модели ().
Модель с одной пространственной и одной химической координатой реакции, обозначенная индексами l и m соответственно.Закрашенные прямоугольники обозначают узкие места. Проектируя химические координаты, как объяснено в тексте, эту модель можно привести к той же форме, что и в. В общем, результирующая эффективная одномерная модель не удовлетворяет предположению о сильной связи уравнения (1). 28.
Распространение наших результатов на отряды и наблюдаемые подшаги в последующих подразделах напрямую мотивировано экспериментальными наблюдениями таких событий (2,3,5).
КЛАСС РАСШИРЕННЫХ МОДЕЛЕЙ
В этом разделе мы немного более подробно описываем большой класс расширенных моделей, которые отображают симметрию времени пребывания, и указываем, как выводится симметрия времени пребывания.Мы используем химическую кинетику, но записываем Основное уравнение с произвольными скоростями перехода w ij из состояния j в i ,
(19)
Ненулевые «диагональные» скорости w ii позволяют, например, описывать необратимые отсоединения двигателей от их дорожек (23,51) или другие события, которые могут быть отфильтрованы экспериментально.
Также необходимо указать условие сильной связи. Один из способов — требовать, чтобы скорости перехода вокруг любого замкнутого контура i 0 , i 1 , i 2 ,…, i m = i 0 из переходы удовлетворяют
(20)
Это свойство автоматически выполняется для последовательных моделей и позволяет определять свободную энергию G j для каждого состояния j с точностью до аддитивной константы.Из подробного баланса, мы имеем для разницы свободной энергии вдоль перехода Следовательно, уравнение. 20 говорит, что сумма разностей свободной энергии вдоль любого замкнутого контура равна нулю, что означает, что потребление свободной энергии, которое не вызывает чистого движения, например, бесполезный гидролиз АТФ, исключено. (Обратите внимание, что механохимический цикл, скажем, из состояния ( k ) в ( k + N ), не является замкнутым циклом в нашем описании.) Мы также предполагаем, что никакой переход не является необратимым, т. Е. w ij ≠ 0 ⇔ w ji ≠ 0, хотя скорости перехода могут быть сколь угодно малыми.
Чтобы отразить циклическую работу моторных белков, скорости перехода являются периодическими с периодом N , и имеется четко определенная свободная энергия за период,
(21)
Важный шаг в выводе уравнения. 1 состоит в том, чтобы сделать вывод, что состояние двигателя сразу после шага не зависит от предыдущих шагов. В последовательной модели это происходит из-за того, что в цикле существует только один переход, производящий ступеньку. Это состояние можно несколько смягчить. Достаточно предположить свойство узкого места, упомянутое во введении, т.е.е., что все переходы, соответствующие шагу, являются либо одним состоянием, либо состоянием узкого места, либо из него, как показано на. Как указывает термин, система должна посещать состояние узкого места каждый раз, когда проходит цикл.
Пример модели со свойством узкого места и N = 6 состояний за цикл. Все состояния внутри заштрихованной области принадлежат одному циклу. Состояния узкого места: 0, ± N , ± 2 N …. Сплошные стрелки обозначают переходы, связанные с механическим шагом длиной d , а пунктирные стрелки указывают переходы внутри цикла, которые невозможно обнаружить.Невозможно перейти от одного цикла к другому, не выйдя из состояния узкого места или не достигнув его. В общем, переходы между любыми состояниями в цикле разрешены, а состояния узких мест могут иметь переход в любое состояние в соседнем цикле.
Верность предположения об узком месте должна определяться для каждой системы отдельно. Например, отклонения от ступенчатой корреляции, предсказанной в формуле. 15 означает, что предположение неверно.
Хотя модели, рассматриваемые в этом разделе, являются более общими, чем последовательные модели, некоторые свойства последовательных моделей сохраняются.К ним относятся сильное связывание, периодичность и то, что шаги (примерно) соответствуют одному переходу в ферментативном цикле. Следовательно, они описывают эффективно одномерное движение, где движения по пространственным координатам и координатам химической реакции (30) тесно связаны друг с другом для движения в обоих направлениях. Следовательно, движение вперед и назад происходит в противоположных направлениях по одним и тем же путям реакции, как и для последовательных моделей.
Симметрия времени пребывания и отслоения
Симметрия времени выдержки для расширенных моделей с отсоединениями может быть получена с использованием тех же методов, что и для последовательных моделей, и более подробная информация об этом выводе приведена в Приложении C.Как и в последовательном случае, периодичность необходима только для установления уравнения. 2, в то время как симметрия времени пребывания, уравнение. 1, следует также без предположения о периодичности.
Примерами непериодического случая являются подциклы, в которых показана модель с двумя наблюдаемыми подшагами на цикл. Каждый шаг в примере удовлетворяет свойству узкого места, но оба состояния узкого места находятся в одном подцикле. Получение симметрии времени выдержки для различных субциклов выполняется, как в Приложении C, с немного разными начальными условиями.
Простая периодическая модель с двумя подшагами на цикл, с длиной шага d 1 и d 2 . Подцикл 1 имеет N 1 состояний, а подцикл 2 имеет N — N 1 состояний. Оба шага обладают свойством узкого места, хотя состояния узкого места 0 и N 1 -1 находятся в подцикле 1. Если сильная связь удовлетворена, оба подцикла отображают симметрию времени задержки.
Как уже говорилось выше, отрыв мотора от его колеи наблюдается в нескольких системах (2,3,5).Мы моделируем отряды, вводя коэффициенты смертности (23,51) в качестве дополнительных членов в диагональные элементы главного уравнения и матрицы M уравнений. 7 и 49.
Наличие отслоений влияет на долгосрочное поведение модели (51), а также на распределения времени пребывания и вероятности попарного расщепления. Вероятности условного отрыва также должны быть добавлены к уравнениям. 6 и 12.
Однако при выводе симметрии времени пребывания в Приложении C скорости перехода всегда вводятся как отношения прямой и обратной скоростей, e.г., в уравнении. 42, так что диагональные элементы ( k m = k m + 1 ) всегда сокращаются. Следовательно, уравнение. 1 остается в силе даже при наличии отрядов.
Наблюдаемые подшаги
Для некоторых двигателей полные шаги вперед и назад делятся на наблюдаемые подшаги (5,17). В этом разделе мы покажем, как связь между вероятностями расщепления в уравнении. 1 можно обобщить, если имеет место сильная связь и все подэтапы удовлетворяют свойству узкого места.
Для начала рассмотрим систему в, которая производит подшаги d 1 и d 2 = d — d 1 во время каждого цикла, и предположим, что каждый подцикл отображает время ожидания симметрия. С этого момента мы обозначаем прямой шаг длиной d 1 с +1 , и аналогично для других подшагов. Отслеживая только d 2 -шагов, мы можем проанализировать систему, как и в предыдущих разделах, используя четыре вероятности расщепления и время ожидания, которые удовлетворяют уравнению.1.
С другой стороны, если мы будем отслеживать и различать все подшаги, мы могли бы вместо этого измерить восемь вероятностей разделения: и так далее.
Суммируя все пути между двумя последовательными +2 -шагами, мы получаем
(22)
и аналогично
(23)
Это означает, что соотношение между свободной энергией и вероятностями расщепления для системы только с один шаг на цикл обобщается до
(24)
Обратите внимание, что мы суммировали все пути между двумя +2 шагов без явной ссылки на все пути, которые начинаются с шага +2 и заканчиваются чем-то еще.Это означает, что уравнение. 24 действителен также для системы с отрывами или с несколькими параллельными путями.
Для систем, которые проходят подэтапы d 1 , d 2 … d K в каждом цикле, мы можем использовать тот же аргумент, чтобы связать вероятности разделения полного анализа (все подэтапы Включено) к тому, где первый подшаг ( d 1 ) игнорируется:
(25)
(26)
Итерация этого преобразования для игнорирования подшагов 2, 3,…, K — 1 , мы находим следующее соотношение для цикла с K видимых подшагов:
(27)
В сложной системе с параллельными путями, где цикл может быть завершен с использованием различных последовательностей подшагов, уравнение.27 выполняется для каждой такой последовательности в отдельности.
Пример модели
В этом разделе мы рассмотрим небольшую, но нетривиальную модель с двумя состояниями на цикл, чтобы представить явный пример, иллюстрирующий результаты предыдущих разделов.
Модель имеет две параллельные траектории, как показано на рисунке, а установившаяся скорость и эффективная дисперсия точно известны (44). Свойство узкого места выполнено, и сильная связь эквивалентна
(28)
Вычислив распределения времени пребывания и вероятностей разделения (подробности см. В Приложении D), мы получаем
(29)
(30)
( 31)
(32)
Пример непоследовательной модели с N = 2 состояния на цикл, с двумя параллельными путями, которые производят шаг в направлении x .Сплошные стрелки представляют собой переходы, создающие ступеньки, а пунктирные стрелки указывают скрытые переходы, которые не приводят к наблюдаемым ступеням. Закрашенные прямоугольники обозначают узкие места.
Собственные значения λ 1, 2 приведены в Приложении D, а c 0 = λ 1 λ 2 > 0. Для этой модели уравнение. 28, очевидно, эквивалентен симметрии времени пребывания уравнения. 1. Для двух других пар ступеней получаем
(33)
(34)
(35)
(36)
Мы видим, что ρ + — ( t ) и ρ — + ( t ) отличаются как друг от друга, так и от распределений ++ и −−, независимо от того, соответствует ли уравнение28 держит или нет. Направления шагов антикоррелированы, так как
(37)
Пример иллюстрирует логику наших результатов. Сильная связь и свойство узкого места вместе являются достаточными условиями для симметрии времени пребывания. Одного свойства узкого места достаточно для описания ступенчатых направлений в уравнении (2) цепью Маркова. 12, который остается в силе, даже если уравнение. 28 не устраивает.
Возможная причина, по которой модель может не удовлетворять уравнению. 28 проиллюстрирован на.Это снова модель состояний N = 2, но с независимой «химической» координатой реакции (верхний индекс m на состояниях), например, количество гидролизованных молекул АТФ (30). Например, путь может быть ступенчатым гидролизом АТФ, в то время как реакция может описывать независимую от АТФ ступень.
Эта модель может быть преобразована в одномерную модель через проекцию, которая не влияет на показатели. Однако открытый путь реакции трансформируется в замкнутый контур. Поскольку сильная связь не накладывает ограничений на скорости в исходной модели, нет причин предполагать, что уравнение.28 для проектируемой модели. В эффективном одномерном описании эта петля затем становится петлей скольжения, которая рассеивает свободную энергию, не производя чистого движения. Следовательно, простые ступенчатые корреляции уравнения. 15, но не симметрия времени пребывания.
В системах, где невозможно измерить «химическое положение» с точностью до одной молекулы, результирующее нарушение симметрии времени пребывания является полезным тестом для таких спроектированных петель скольжения, если выполняется свойство узкого места.Это свойство, в свою очередь, можно исключить, например, если ступенчатые корреляции более сложны, чем предсказано в формуле. 15.
Наиболее интересными кандидатами для таких испытаний, по-видимому, являются роторные двигатели, приводимые в движение потоками ионов, например, часть F O АТФ-синтазы или бактериальный жгутиковый двигатель, поскольку трудно измерить поток ионов с помощью точность до одной молекулы. Нам не известны какие-либо эксперименты с АТФ-синтазой в условиях, которые производят как прямые, так и обратные шаги.Данные от жгутикового двигателя будут проанализированы в следующем разделе.
Применение к жгутиковому мотору
В этом разделе мы применяем наши теоретические результаты для анализа шаговых данных из недавнего эксперимента с химерным жгутиковым мотором (18). Как мы увидим, данные согласуются с предсказанной симметрией времени пребывания и ступенчатыми корреляциями в пределах экспериментальной неопределенности. Мы также оцениваем свободную энергию за цикл и показываем, что оценка, основанная на завершении цикла, может иметь значительную систематическую ошибку по сравнению с формулой.1b.
Мотор жгутика продвигает множество плавающих бактерий, управляя вращением нитей жгутика. Каждая нить приводится в движение в основании трансмембранным роторным двигателем, приводимым в действие потоком ионов (Na + в данном случае (18)) вниз по электрохимическому градиенту через клеточную мембрану. Диаметр двигателя составляет ~ 45 нм, и предполагается, что он содержит 13 блоков, генерирующих крутящий момент (18,52). В этом эксперименте была активна только одна единица, и ожидается, что жгутик будет переключаться между 26 различными ориентациями за оборот, что соответствует длине шага 360 ° / 26 ≈ 14 ° (18).Мы проанализировали одну траекторию с близкой к нулю чистой скоростью и одну с конечной скоростью.
С помощью фильтрации Чанга-Кеннеди (53) для улучшения шагов и алгоритма поиска шагов, описанного в Sowa et al. (18) необработанные данные были преобразованы в данные о ступенях лестницы, как показано на. При внимательном рассмотрении кажется, что траектория разделена на интервалы, где длины шагов согласуются друг с другом, но не совпадают по фазе с шагами снаружи. Этот очевидный дрейф может быть связан с динамической заменой блоков статора (54), которые прикрепляют двигатель к ячейке.
Мы определили интервалы последовательного шага путем осмотра (см.) И исключили дрейф из нашего анализа, рассматривая непоследовательные шаги как отслоения, то есть каждый интервал последовательного шага рассматривался как независимый прогон. Результат суммирован в, и теперь мы переходим к сравнению корреляций шаг-шаг и распределения времени пребывания от траектории A с теоретическими предсказаниями. Траектория B содержала слишком мало шагов, чтобы сделать такие сравнения значимыми.
ТАБЛИЦА 1
событий шагов (±) и дрейфа ( δ ) для двух проанализированных ступенчатых траекторий
| ij | + | — | δ| ++ | | —+ δ | — + | — | — δ | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Траектория A | n ij | 108 | 103 | 13 | 30 | 68 | 10 | 69 | 30 | 3 | |||||||||||||
| 253 iπ | |||||||||||||||||||||||
| 25329 iπ48 | 0,46 | 0,06 | 0,28 | 0,63 | 0,09 | 0,68 | 0,29 | 0,03 | |||||||||||||||
| n ij | 43 | 27 | 11 | 20 | 16 | 6 | 17 | 5 | 5 | 9109 | |||||||||||||
| 0,33 | 0,14 | 0,48 | 0,38 | 0,14 | 0,63 | 0,19 | 0,19 |
Шаг-шаговая автокорреляционная функция показана для траектории . Прогноз C ( n ) / C (0) = γ n уравнения. 13 действительно для траекторий без отрывов. Поэтому для сравнения теории и экспериментов вероятности расщепления должны быть перенормированы на фактор (чтобы учесть тот факт, что интервалы согласованного шага (по определению) не содержат событий дрейфа.Это дает теоретическое предсказание
(38)
Подгонка методом наименьших квадратов к экспериментальным корреляциям дает γ = -0,40, что согласуется с уравнением. 38, но несовместимы с некоррелированными шагами.
Подтвердив, что ступенчатые корреляции согласуются с уравнением. 16 мы переходим к проверке симметрии времени пребывания. Построены эмпирические функции распределения P ± ( t ) для траектории A . Планки погрешностей — это стандартные отклонения от оценок начальной загрузки (55).Используя критерий Колмогорова-Смирнова (56), мы заключаем с достоверностью 95%, что τ — + имеют другое распределение, чем τ ++ и τ −− , и что τ + — имеют другое распределение, чем τ −− . Однако тест не смог обнаружить значительных различий между тремя другими парами (++ / −−, + — / −− и + — / — +). Это снова согласуется с теоретическими предсказаниями, а также показывает, что статистика достаточно хороша, чтобы обнаруживать различия между неравными распределениями.Также интересно отметить, что τ ++ и τ −− в среднем длиннее τ + — и τ — + . Это разумно, поскольку для событий + — / — + в принципе требуется только один переход, в то время как система должна пройти полный цикл, чтобы завершить событие ++ или −−.
Ионная движущая сила не была измерена независимо (18), поэтому невозможно сравнить оценку свободной энергии по формуле.1 с экспериментальным значением. Однако мы можем сравнить наш результат с результатом, основанным на формуле. 2, который использовался в Sowa et al. (18). Результаты представлены в. Как и ожидалось, свободная энергия за цикл близка к нулю в траектории A , которая почти не имеет чистой скорости, в то время как траектория B явно имеет конечную свободную энергию за цикл для вращения. Также обратите внимание на различия в оценках, основанных на формуле. 1 и уравнение. 2, которые показывают, что оценка завершения цикла может приводить к значительным систематическим ошибкам в оценках свободной энергии, если применяется к данным шага.
ТАБЛИЦА 2
Оценки свободной энергии для траекторий A и B , в единицах k B T
| Δ G 90Δ9 циклов | ||||
|---|---|---|---|---|
| Траектория A | 0,06 ± 0,23 | -0,05 ± 0,10 | ||
| Траектория B | -0,94 ± 0,28 | -0,46 ± 0,28 | -0,46 ± 0,28 | -0,46 Статистические свойства шагов в обратимых молекулярных моторах не такие же, как у завершений цикла в кинетике ферментов.Это различие необходимо учитывать для правильной интерпретации траекторий шага. В этой статье мы расширили теорию для времен пребывания в последовательных моделях (20,21) и вывели соотношение симметрии для условных распределений времени пребывания для большого класса экспериментально значимых моделей, включая параллельные пути, видимые подшаги, и отряды. В отличие от статистики завершений цикла (23–25), распределения времени задержки и вероятности разделения шагов зависят от направления шагов обоих шагов до и после периода задержки. Симметрия времени пребывания является следствием сильной связи, то есть сильной связи для шагов вперед и назад, а также свойства узкого места лежащей в основе кинетической схемы. Это означает, что движение системы по сути является одномерным случайным блужданием в (двумерном) пространстве пространственных координат и координат химической реакции. Это позволяет использовать наши результаты для вывода информации о сцеплении и эффективности системы на основе кинетических данных без подробных предположений о лежащей в основе кинетической схеме.В этом отношении это аналогично соотношению r ≥ 1/ N между параметром случайности r и числом шагов N в механохимическом цикле молекулярных двигателей (28,57,58). Альтернативой используемому здесь дискретному формализму является включение непрерывных пространственных степеней свободы, как это обычно бывает, например, при моделировании моторных механизмов храпового типа (30,49,50). Поскольку такие модели могут быть дискретизированы (42), в принципе возможно исследовать сильную связь и свойство узких мест также в непрерывных моделях.Примером этого является диффузия в одном измерении (см.), Которая строго удовлетворяет сильной связи и свойству узкого места. Интересной проблемой для дальнейших исследований является количественная оценка того, насколько хорошо сохраняется симметрия времени пребывания в системе с небольшими отклонениями от этих предположений. Мы проанализировали шаговые данные от отдельных моторных субъединиц в жгутичном моторе (18). Данные, по-видимому, согласуются с предсказанной симметрией времени пребывания и корреляциями шаг-шаг, хотя только одна траектория с почти нулевой скоростью имела достаточно шагов, чтобы сделать такое сравнение значимым. Форма ступенчатых корреляций согласуется с лежащей в основе кинетической схемой, которая удовлетворяет свойству узкого места. Итак, указывает ли симметрия времени пребывания на то, что субъединицы жгутикового двигателя сильно связаны с движущим потоком ионов? Другая возможность состоит в том, что ступеньки представляют собой колебания равновесия, на что указывает низкое значение Δ G , оцененное на основе вероятностей ступенек. В равновесии нет изменения свободной энергии, связанного с переносом ионов, что означает, что симметрия времени пребывания может быть получена также для системы со слабой связью.Чтобы сказать что-либо о связи в жгутичном двигателе, необходимо проверить симметрию времени пребывания в режиме с конечной (и постоянной) скоростью и ионной движущей силой. В принципе, это вопрос наблюдения большего количества шагов в таких условиях, но также был бы полезен систематический способ выявления и отделения шагов от событий дрейфа. Шаг-шаг корреляции, предсказанные в уравнении. 15 может присутствовать также в системах, которые нарушают симметрию времени пребывания. Отклонения от этой формы могли бы кое-что сказать о топологии кинетических путей в таких системах, и, вероятно, было бы полезно применить наш анализ также к кинезину и миозину V. Точная теоретическая модель часто имеет решающее значение для правильной интерпретации экспериментов с такими сложными системами, как системы моторных белков. Многие предыдущие теоретические работы о шагах и времени пребывания в молекулярных двигателях (22,23,26,27) основаны или предполагают описания, в которых последовательные шаги или циклы статистически независимы друг от друга. Как мы продемонстрировали, это не относится к жгутиковому мотору Sowa et al. (18). Мы также представили большой класс простых моделей, в которых коррелируют легко доступные величины, такие как время пребывания и направление шага. Мы ожидаем, что наши результаты будут полезны как при анализе данных, так и при планировании экспериментов. В частности, мотивированы дальнейшие экспериментальные усилия для обнаружения корреляций и сбора важной статистики как для прямых, так и для обратных шагов. Благодарности поделился своей работой (25) перед публикацией. Благодарим за финансовую поддержку Королевского технологического института, Фонда Валленберга (для M.L.) и Шведского исследовательского совета, грант № 2003-5001 (для M.W.). ПРИЛОЖЕНИЕ AТеперь мы дадим подробный вывод уравнения. 1 для последовательной модели. Начальным условием является состояние сразу после шага, и его можно записать (39) Чтобы вывести уравнение. 1, мы вычисляем и используя уравнение. 8 и начальные условия в уравнении. 39. Это дает (40) , где суммирование k 1 , k 2 ,… идет от 0 до N — 1.Тот же расчет для P −− ( t ) дает (41) Произведения матричных элементов в уравнениях. 40 и 41 соответствуют n -шаговых путей между состояниями 0 и N -1, плюс дополнительный шаг выхода. Для последовательных моделей кратчайший такой путь составляет N шагов, поэтому первые производные N — 1 равны нулю. Для n ≥ N отметим, что существует взаимно однозначное соответствие между ненулевыми членами в уравнении.40 и уравнение. 41. Для каждого члена, включая путь от 0 до N — 1 в уравнении. 40, есть соответствующий член для обратного пути от N — 1 до 0 в уравнении. 41. Отношение двух соответствующих ненулевых членов составляет (42) Возвращаясь к уравнению. 7 для элементов M , и используя по периодичности w 0 = w N , мы видим, что для всех пар соответствующих членов. Кроме того, P ++ (0) = P −− (0) = 0, поскольку нет перехода, который производит два шага одновременно.Следовательно, (43) для всех n ≥ 0. Основная причина состоит в том, что сумма изменений свободной энергии одинакова на всех возможных путях на один цикл вперед от 0. Начиная с P + + ( t ) и P −− ( t ) являются интегралами решений сокращенного основного уравнения, которое представляет собой конечную систему обыкновенных дифференциальных уравнений с постоянными коэффициентами, они являются гладкими функциями, которые имеют Серия Тейлора.Следовательно, уравнение. 43 вместе с нормализацией в формуле. 10 следует уравнение. 1. Подобное соответствие между путями было использовано в Wang и Qian (25) для вывода уравнения. 2. Периодичность необходима, чтобы получить простую связь между π ++ , π −− и Δ G в уравнении. 1b, но не для установления симметрии времени пребывания в уравнении. 1а. Без периодичности уравнение. 2 заменяется на (44) ПРИЛОЖЕНИЕ BЧтобы получить явные выражения для ρ ++ ( t ) и ρ −− ( t ) для последовательных моделей, мы Во-первых, обратите внимание, что вероятности занятия q j ( t ) в уравнении.8 являются решением системы линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами, а именно элементы M в уравнении. 7. Если собственные значения { λ j } M невырожденные, решения имеют вид Обратите внимание, что собственные значения имеют отрицательные действительные части, чтобы гарантировать, что система в конечном итоге выйдет из интервала. Мы составляем анзац (45) , где член 1 обеспечивает правильную нормализацию. Нам потребуется N уравнений для определения коэффициентов α j .Это (46) для 0 ≤ k ≤ N — 1. Случай k = 0 обсуждался непосредственно перед формулой. 43, а 1 ≤ k ≤ N — 1 следует из аргумента между уравнениями. 41 и 42. Результирующая система уравнений для α j относится к типу Вандермонда, (47) Решая по правилу Крамера и полагая (48) , мы приходим к уравнению. 11. Распределения τ + — и τ + — можно вычислить с помощью того же анзаца, но производные и не равны нулю при k ≥ 1, поэтому результаты более сложны и в целом нет простой связи между ρ + — ( т ) и ρ — + ( т ). ПРИЛОЖЕНИЕ CВ этом Приложении мы выводим уравнение. 1 для периодической расширенной модели, подобной модели в, обобщающей задачу первого перехода по мере продвижения. Вывод происходит так же, как и для последовательной модели, путем решения сокращенного главного уравнения для состояний 0, 1,…, N — 1, (49) с поглощающими границами на -1 и N , и позволяя w ii ≥ 0 моделировать отряды. Обратите внимание, что сумма в формуле. 49 имеет не более 2 N — 1 члена из-за свойства узкого места.После шага вперед система находится в состоянии 0, хотя в принципе она может быть где угодно в цикле после шага назад. Таким образом, начальные условия, описывающие распределение состояний сразу после шага ±, равны (50) Поскольку существует несколько переходов выхода для каждого шага, уравнение. 8 для функций вероятности времени пребывания обобщается до (51) Теперь перейдем к вычислению производных от P ++ (0) и P −− (0), и отметим, что Уравнения.20 и 21, разность свободной энергии G N — G 0 = Δ G не зависит от пути: (52) (53) С периодичностью w ij выражается в формуле. 22, получаем z — ′ = z — , что доказывает уравнение. 43 и, следовательно, уравнение. 1. Вывод для случая, когда шаги назад (вместо шагов вперед) заканчиваются в состоянии узкого места, аналогичен. Обратите внимание, что наше определение свойства «узкое место» означает, что нет переходов, которые производят два шага одновременно.Это исключает разрывы при t = 0 в функциях распределения P ± ( t ) и оправдывает использование нами разложений Тейлора. ПРИЛОЖЕНИЕ DВ этом Приложении мы решаем примерную модель в некоторых деталях. Помимо вывода уравнений. 29–37, это также иллюстрирует метод, который можно легко обобщить на более крупные системы и реализовать в системах компьютерной алгебры. Для N ≥ 5 состояний за цикл собственные значения λ j должны быть вычислены численно.За этим исключением, метод дает явные выражения для распределений времени пребывания в области реального времени, которые можно напрямую сравнивать с экспериментальными гистограммами времени пребывания. Первая проблема выхода для модели в регулируется сокращенным Основным уравнением, как описано в Ур. 49, с матрицей (54) Собственные значения M равны (55) и удовлетворяют соотношениям (56) (57) Начальные условия после шагов вперед и назад даются формулой.50, а условные распределения времени пребывания задаются формулой. 51: (58) (59) (60) Использование анзаца в уравнении. 45 вместе с уравнениями. 58–60 для расчета ∂ t π ± — P ± — ( t ) и ∂ t π ± + ± (P t ), получаем следующие системы линейных уравнений: (61) Решая это и используяρ ± ± ( t ) = ∂ t P ± ± ( t ), мы в конечном итоге приходим к функциям плотности вероятности, приведенным в уравнениях.29–36. Наконец, нам нужны выражения для вероятностей расщепления, которые мы выводим с помощью сопряженных уравнений (19). Пусть π j ± , где j = 0, 1, будет вероятностью того, что система, начиная с состояния j , затем произведет шаг ±. Начиная с π 0−, отметим, что из состояния 0 шаг назад может быть выполнен либо следующим переходом, являющимся шагом назад, который имеет вероятность ( b + w 0 ) / ( a + b + u 0 + w 0 ), или путем перехода в состояние 1 и оттуда в конечном итоге получить шаг назад.Последняя возможность имеет полную вероятность π 1− u 0 / ( a + b + u 0 + w 0 ), так что (62 ) Затем мы умножаем и переставляем слагаемые. Применяя ту же процедуру для других π j ± , мы наконец получаем (63) Чтобы получить вероятности попарного расщепления в уравнениях. 29–37, мы сначала решаем π j ± , а затем взвешиваем их в соответствии с начальными условиями уравнения.58: (64) Ссылки1. Картер, Н. Дж., И Р. А. Кросс. 2005. Механика кинезинового шага. Природа. 435: 308–312. [PubMed] [Google Scholar] 2. Нисияма М., Х. Хигучи и Т. Янагида. 2002. Хемомеханическое соединение прямых и обратных шагов отдельных молекул кинезина. Nature Cell Biol. 4: 790–797. [PubMed] [Google Scholar] 3. Ю. Танигучи, М. Нишияма, Ю. Исии и Т. Янагида. 2005. Энтропия исправляет броуновские ступени кинезина. Nature Chem. Биол. 1: 342–347.[PubMed] [Google Scholar] 4. Гайдош, Н. Р., и С. М. Блок. 2006. Обратные шаги, индуцированные аналогами нуклеотидов, предполагают, что передняя головка кинезина управляется штаммом. Proc. Natl. Акад. Sci. США. 103: 8054–8059. [Бесплатная статья PMC] [PubMed] [Google Scholar] 5. Уэмура С., Х. Хигучи, А. О. Оливарес, Э. М. Де Ла Крус и С. Ишивата. 2004. Механохимическое соединение двух подэтапов в одном двигателе миозина V. Nat. Struct. Мол. Биол. 11: 877–883. [PubMed] [Google Scholar] 6. Риф, М., Р. С. Рок, А. Д. Мехта, М.S. Mooseker, R. E. Cheney и J. A. Spudich. 2000. Кинетика ступенчатого действия миозина-V: молекулярная модель процессивности. Proc. Natl. Акад. Sci. США. 97: 9482–9486. [Бесплатная статья PMC] [PubMed] [Google Scholar] 7. Клемен, А. Э.-М., М. Вильфан, Дж. Дж. Цзюньшан Чжан, М. Берманн и М. Риф. 2005. Силозависимая кинетика шагания миозина-V. Биофиз. J. 88: 4401–4410. [Бесплатная статья PMC] [PubMed] [Google Scholar] 8. Кристоф, Дж., М. Гебхардт, А. Э.-М. Клемен, Дж. Джод и М. Риф. 2006. Myosin-V — механический храповик.Proc. Natl. Акад. Sci. США. 103: 8680–8685. [Бесплатная статья PMC] [PubMed] [Google Scholar] 9. С. Тоба, Т. М. Ватанабэ, Л. Ямагути-Окимото, Ю. Ю. Тоошима и Х. Хигучи. 2006. Перекрывающийся передаточный механизм одиночной молекулярной подвижности цитоплазматического динеина. Proc. Natl. Акад. Sci. США. 103: 5741–5745. [Бесплатная статья PMC] [PubMed] [Google Scholar] 10. Abbondanzieri, E. A., W. J. Greenleaf, J. W. Shaevitz, R. Landick и S. M. Block. 2005. Прямое наблюдение шагового перехода пар оснований с помощью РНК-полимеразы.Природа. 438: 460–465. [Бесплатная статья PMC] [PubMed] [Google Scholar] 11. М. Диц, Б. Циммерманн, М. Бёрш, М. Кёниг, Э. Швайнбергер, С. Стейгмиллер, Р. Рейтер, С. Фелекян, В. Кудрявцев, К. А. М. Зайдель и П. Гребер. 2004. Протонное вращение субъединицы в единственной мембраносвязанной F 0 F 1 -АТФ-синтаза. Nat. Struct. Мол. Биол. 11: 135–141. [PubMed] [Google Scholar] 12. Уэно, Х., Т. Судзуки, К. Киносита, младший, и М. Йошида. 2005. АТФ-управляемое ступенчатое вращение F 0 F 1 -АТФ-синтазы.Proc. Natl. Акад. Sci. США. 102: 1333–1338. [Бесплатная статья PMC] [PubMed] [Google Scholar] 13. Ясуда Р., Х. Нодзи, К. Киносита-младший и М. Йошида. 1998. F 1 -ATPase Это высокоэффективный молекулярный мотор, который вращается с дискретными шагами 120 °. Клетка. 93: 1117–1124. [PubMed] [Google Scholar] 14. Ясуда Р., Х. Нодзи, М. Йошида, К. Киносита-младший и Х. Ито. 2001. Разрешение различных подшагов вращения с помощью субмиллисекундного кинетического анализа F1-АТФазы. Природа. 410: 898–904. [PubMed] [Google Scholar] 15.Симабукуро К., Р. Ясуда, Э. Мунеюки, К. Ю. Хара, К. Киносита-младший и М. Йошида. 2003. Катализ и вращение двигателя F 1 : расщепление АТФ на каталитическом сайте происходит за 1 мс перед подшаговым вращением на 40 °. Proc. Natl. Акад. Sci. США. 100: 14731–14736. [Бесплатная статья PMC] [PubMed] [Google Scholar] 16. Симабукуро К., Э. Мунеюки и М. Йошида. 2005. Альтернативный путь реакции F1-АТФазы, предложенный вращением без подшагов 80 ° / 40 ° вялого мутанта при низком уровне АТФ. Биофиз.J. 90: 1028–1032. [Бесплатная статья PMC] [PubMed] [Google Scholar] 17. Нишизака, Т., К. Оива, Х. Нодзи, С. Кимура, Э. Мунеюки, М. Йошида и К. Киносита, мл. 2004. Хемомеханическое связывание в F 1 -АТФазе выявлено путем одновременного наблюдения за кинетикой нуклеотидов. и вращение. Nat. Struct. Мол. Биол. 11: 142–148. [PubMed] [Google Scholar] 18. Sowa, Y., A. D. Rowe, M. C. Leake, T. Yakushi, M. Homma, A. Ishijima и R. M. Berry. 2005. Прямое наблюдение за ступенями вращения жгутикового мотора бактерий.Природа. 437: 916–919. [PubMed] [Google Scholar]19. Ван Кампен, Н. Г. 1992. Стохастические процессы в физике и химии, 2-е изд. Издательство Elsevier Science Publishers, Амстердам, Нидерланды. 20. Цыганков Д., Линден М., Фишер М. Э. 2007. Скрытые подэтапы в каталитическом цикле молекулярных моторов: условные вероятности шага и время ожидания. Phys. Ред. E. 75: 021909. [PubMed] [Google Scholar] 21. Цянь, Х. 1997. Простая теория кинетики и энергетики моторных белков. Биофиз. Chem.67: 263–267. [PubMed] [Google Scholar] 22. Коломейский А.Б., Фишер М.Э. 2003. Простая кинетическая модель описывает процессивность миозина-V. Биофиз. J. 84: 1642–1650. [Бесплатная статья PMC] [PubMed] [Google Scholar] 23. Коломейский А.Б., Стукалин Е.Б., Попов А.А. 2005. Понимание механохимического связывания в кинезинах с использованием процессов первого прохождения. Phys. Ред. E. 71: 031902. [PubMed] [Google Scholar] 24. Цянь Х. и Х. Сунней Се. 2006. Обобщенное уравнение Холдейна и флуктуационная теорема в кинетике стационарного цикла отдельных ферментов.Phys. Ред. E. 74: 010902 (R). [PubMed] [Google Scholar] 25. Ван Х. и Х. Цянь. 2007. О детальном балансе и обратимости полумарковских процессов и кинетики одномолекулярных ферментов. J. Math. Phys. 48: 013303. [Google Scholar] 26. Шаевиц, Дж. У., С. М. Блок и М. Дж. Шнитцер. 2005. Статистическая кинетика макромолекулярной динамики. Биофиз. J. 89: 2277–2285. [Бесплатная статья PMC] [PubMed] [Google Scholar] 27. Сантос, Дж. Э., Т. Франош, А. Пармеджиани и Э. Фрей. 2005. Процессы обновления и флуктуационный анализ молекулярного моторного шага.Phys. Биол. 2: 207–222. [PubMed] [Google Scholar] 28. Свобода К., Митра П. П., Блок С. М.. 1994. Анализ флуктуаций движения моторных белков и кинетики отдельных ферментов. Proc. Natl. Акад. Sci. США. 91: 11782–11786. [Бесплатная статья PMC] [PubMed] [Google Scholar]29. Ховард Дж. 2001. Механика моторных белков и цитоскелета. Sinauer Associates, Сандерленд, Массачусетс. 30. Бустаманте, К., Д. Келлер и Г. Остер. 2001. Физика молекулярных моторов. В соотв. Chem. Res. 34: 412–420. [PubMed] [Google Scholar] 31.Ито, Х., А. Такахаши, К. Адачи, Х. Нодзи, Р. Ясуда, М. Йошида и К. Киносита, мл. 2004. Механически управляемый синтез АТФ с помощью F 1 -АТФазы. Природа. 427: 465–468. [PubMed] [Google Scholar] 33. Милеску, Л. С., А. Йылдыз, П. Р. Селвин и Ф. Сакс. 2006. Оценка максимального правдоподобия молекулярной моторной кинетики по последовательностям времени пребывания на лестнице. Биофиз. J. 91: 1156–1168. [Бесплатная статья PMC] [PubMed] [Google Scholar] 34. Милеску, Л. С., А. Йылдыз, П. Р. Селвин и Ф. Сакс. 2006. Извлечение временных последовательностей из процессивных молекулярных моторных данных.Биофиз. J. 91: 3135–3150. [Бесплатная статья PMC] [PubMed] [Google Scholar] 35. МакКинни, С. А., Ч. Джу и Т. Ха. 2006. Анализ траекторий FRET одиночных молекул с использованием скрытого марковского моделирования. Биофиз. J. 91: 1941–1951. [Бесплатная статья PMC] [PubMed] [Google Scholar] 36. Смит, Д. А., В. Стеффен, Р. М. Симмонс и Дж. Сон. 2001. Скрытые-марковские методы для анализа данных о замещении одиночных молекул актомиозина: дисперсионно-скрытый-марковский метод. Биофиз. J. 81: 2795–2816. [Бесплатная статья PMC] [PubMed] [Google Scholar]37.Хилл, Т. Л. 1989. Свободная трансдукция энергии и кинетика биохимического цикла. Спрингер-Верлаг, Нью-Йорк. 38. Фишер М.Э., Коломейский А.Б. 2001. Простая механохимия описывает динамику молекул кинезина. Proc. Natl. Акад. Sci. США. 98: 7748–7753. [Бесплатная статья PMC] [PubMed] [Google Scholar] 40. Гао Ю., В. Ян и М. Карплюс. 2005. Модель на основе структуры для синтеза и гидролиза АТФ F1-АТФазой. Клетка. 123: 195–205. [PubMed] [Google Scholar] 42. Ван Х., С.С. Пескин и Т.К. Элстон. 2003. Надежный численный алгоритм для изучения процессов биомолекулярного транспорта. J. Theor. Биол. 221: 491–511. [PubMed] [Google Scholar] 43. Бир М., И. Дереньи, М. Костур и Р. Д. Астумян. 1999. Внутрискважинная релаксация передемпфированных броуновских частиц. Phys. Rev. E. 59: 6422–6432. [PubMed] [Google Scholar] 44. Коломейский, А. Б. 2001. Точные результаты для кинетических моделей биотранспорта с параллельными цепями. J. Chem. Phys. 115: 7253–7259. [Google Scholar] 45. Бейкер, Дж.Э., Кременцова Е.Б., Г.Дж. Кеннеди, А. Армстронг, К. М. Трибус и Д. М. Уоршоу. 2004. Процессивность миозина V: множественные кинетические пути для координации головы к голове. Proc. Natl. Акад. Sci. США. 101: 5542–5546. [Бесплатная статья PMC] [PubMed] [Google Scholar] 49. Рейманн, П. 2002. Броуновские двигатели: шумный транспорт далеко от равновесия. Phys. Rep. 361: 57–265. [Google Scholar] 50. Jülicher, F., A. Ajdari, and J. Prost. 1997. Моделирование молекулярных моторов. Ред. Мод. Phys. 69: 1269–1282. [Google Scholar] 51. Коломейский А.Б., М.Е.Фишер. 2000. Периодические последовательные кинетические модели с прыжками, ветвлением и смертью. Physica A. 279: 1–20. [Google Scholar] 52. Берг, Х. С. 2003. Роторный двигатель бактериальных жгутиков. Анну. Rev. Biochem. 72: 19–54. [PubMed] [Google Scholar] 53. Чанг, С. Х. и Р. А. Кеннеди. 1991. Метод прямой-обратной нелинейной фильтрации для извлечения небольших биологических сигналов из шума. J. Neurosci. Методы. 40: 71–86. [PubMed] [Google Scholar] 54. Reid, S. W., M. C. Leake, J. H. Chandler, C.-J. Ло, Дж. П.Армитаж и Р. М. Берри. 2006. Максимальное количество генерирующих крутящий момент единиц в жгутичном двигателе Escherichia coli составляет не менее 11. Proc. Natl. Акад. Sci. США. 103: 8066–8071. [Бесплатная статья PMC] [PubMed] [Google Scholar]55. Press, W. H., S. A. Teukolsky, W. T. Vetterling и B.P. Flannery. 1992. Числовые рецепты на C, 2-е изд. Издательство Кембриджского университета. 56. Барлоу Р. Дж. 1989. Статистика. Уайли, Чичестер, Англия. 57. Коза, З. 2002. Максимальная сила молекулярного двигателя.Phys. Ред. E. 65: 031905. [PubMed] [Google Scholar] 58. Фишер М.Е., Коломейский А.Б. 1999. Молекулярные моторы и силы, которые они проявляют. Physica A. 274: 241–266. [Google Scholar]Engine Неуверенность в прочтении [Архив] — DMCTalk ForumИногда да, но не так много сейчас. Подведу итог недавним наблюдениям.У меня есть счетчик времени ожидания Actron. Также у меня есть шестигранный ключ с Т-образной рукояткой на 3 мм, и мой защитный колпачок уже был снят, когда я получил свою машину, и с тех пор резиновая заглушка DMCH находится в отверстии. Совсем недавно, в том числе сегодня, автомобиль простаивал сразу после запуска из холодного состояния, и остановка стабильно сохранялась в диапазоне 50-60. (Цифры выдержки, на которые я ссылаюсь, — это то, что считывается по 8-цилиндровой шкале и затем умножается на 2). То же, что и у меня. Здесь все хорошо. Это будет так в течение одной или двух минут, а затем, кажется, будет стабильно оставаться на уровне 44. Он будет стабильно держаться на уровне 44 большую часть времени, даже после того, как я достаточно прогрел машину на холостом ходу, чтобы толкнуть охлаждающие вентиляторы включаются и выключаются. Иногда, случайно или по совпадению увеличения оборотов, машина будет пульсировать, а не оставаться на том же постоянном уровне 44 .Однако пульсация намного выше, чем при центрировании около 40 (что вы имели в виду под 20 градусами, Рон), и будет до 75, а затем до 44 или около того. Он не делает это ужасно постоянно, так как временами кажется, что он мигает, когда опускается до 44, а затем хочет пульсировать около 40, как я хотел бы видеть, как это происходит, но затем он либо вернется к максимальному и широкому диапазон пульсирует или просто держится стабильно на уровне 44. Ранние измерения и другие наблюдения указывали на то, что моя машина была настроена на богатый режим, поэтому я намеревался немного наклонить ее.Сняв резиновую заглушку, я услышал отчетливое изменение характеристик двигателя (влияние утечки вакуума?). Да, это утечка вакуума. Всегда закрывайте отверстие пальцем, проверните двигатель один раз, чтобы очистить его, и немного подождите, пока он не успокоится, а затем снимите показания! Я также заметил, что когда вы закрепляете гаечный ключ в отверстии, вы можете довольно легко надавить на узел рычага, с которым он все соединен, и заставить двигатель изменить шаг или разбрызгивание или что-то еще.Я бы предположил, что этого следовало ожидать, посмотрев на схему системы в руководстве по ремонту и увидев, что там происходит. Диагностическая таблица руководства для станций технического обслуживания, когда постоянное свечение на отметке 40-50 указывает на то, что датчик кислорода отключен. Я не думаю, что мой физически отключен, во всяком случае, то, что видно на проводе или разъеме. Я бы подумал, что это говорит мне, что датчик загрязнен или неисправен, так или иначе, да? У меня есть запасной кислородный датчик, который я могу поставить, но еще не сделал. Я перечитал Дэвида, говоря, что все остальное должно быть идеально, поэтому предположим, что должен быть установлен новый и / или надежный кислородный датчик, прежде чем вы сможете уверенно перейти к последнему этапу регулировки смеси CO? Планируется, что следующим шагом будет замена кислородного датчика? да / нет? Да (Если не как с * выше.) Вы выполнили ВСЕ тесты в D: 04: 15? Механика тканей определяет быструю адаптирующуюся и симметричную реакцию на прикосновение.ЗначимостьЗаписи тельцов Пачини в 1960-х годах показали, что прикосновение вызывает симметричную активацию с последующей быстрой адаптацией.Синусоидальная стимуляция приводит к удвоению частоты в чувствительной полосе частот, что позволяет предположить, что эти рецепторы функционируют как частотно-настроенные датчики вибрации. В то время было предложено, чтобы окружающая пластинчатая капсула генерировала эту динамику отклика, действуя как механический фильтр. Однако подобная динамика ответа с тех пор наблюдалась у многих других механорецепторов, что привело к спорам по поводу специфичности этой гипотезы. Используя сочетание электрофизиологии in vivo, механической стимуляции с обратной связью и моделирования, мы разрешаем этот спор в пользу механического фильтра системного уровня, который не зависит от конкретных анатомических особенностей или конкретных каналов механоэлектрической трансдукции. AbstractВзаимодействие с физическим миром глубоко укоренилось в нашем чувстве осязания и зависит от ансамблей соматосенсорных нейронов, которые проникают в кожу и иннервируют ее. Соматосенсорные нейроны преобразуют механическую энергию, доставляемую при каждом прикосновении, в возбуждающие мембранные токи, переносимые по каналам механоэлектрической трансдукции (МЭП). Тельца Пачини у млекопитающих и нейроны рецепторов прикосновения (TRN) у нематод Caenorhabditis elegans встроены в особые специализированные вспомогательные структуры, имеют низкие пороги активации и быстро адаптируются к приложению и снятию механических нагрузок.Недавно были идентифицированы многие из белков-партнеров, которые формируют нативные каналы MeT в этих и других соматосенсорных нейронах. Однако биофизический механизм симметричных реакций на начало и смещение механической стимуляции ускользнул от понимания в течение десятилетий. Более того, неизвестно, активирует ли приложенная сила или возникающее в результате вдавливание каналы MeT. Здесь мы представляем систему для одновременной регистрации мембранного тока, приложенной силы и результирующей вмятины у живых C.elegans (Приложение механических нагрузок с обратной связью в сочетании с нейрофизиологией in vivo, FALCON) и использовать его вместе с моделированием для изучения этих вопросов. Мы показываем, что амплитуда тока увеличивается с вдавливанием, а не с силой, и что быстрые стимулы вызывают большие токи, чем более медленные стимулы, вызывающие такое же или меньшее вдавливание. Модель, связывающая вдавливание тела с активацией MeT-канала через встроенный вязкоупругий элемент, воспроизводит экспериментальные данные, предсказывает, что TRN функционируют как полосовой механический фильтр, и обеспечивает общий механизм для симметричной и быстрой адаптации активации MeT-канала, относящейся к соматосенсорным нейронам через типы и субмодальности. Наше восприятие и реакция на окружающий физический мир глубоко уходят корнями в наше осязание. Ощущение боли имеет решающее значение для выживания, и даже самые легкие прикосновения жизненно необходимы. Например, отсутствие тактильных сенсорных стимулов в начале жизни отрицательно сказывается на росте и развитии нейронов (1). Кожа млекопитающих поражена множеством механорецепторных нейронов, которые различаются по своей чувствительности к механическим нагрузкам, динамике реакции и структуре (2, 3).Такое разнообразие делает ощущение прикосновения устойчивым, но также усложняет попытки расшифровать его биофизические, генетические и молекулярные основы. В то время как недавний анализ канала Piezo2 обеспечивает критическую отправную точку для будущих исследований (4–7) молекул, ответственных за прикосновение, в настоящее время мало что известно о том, как внешние механические нагрузки активируют каналы сенсорной механоэлектрической трансдукции (MeT) у любого животного. . Еще меньше известно о том, как кожа передает и фильтрует механическую энергию.Чтобы исследовать эти вопросы, мы использовали экспериментальные преимущества нематоды Caenorhabditis elegans , в том числе возможность получать записи патч-кламп целых клеток от идентифицированных механорецепторных нейронов у живых животных. Взрослые особи Гермафродиты C. elegans , как известно, имеют пять классов механорецепторных нейронов, которые демонстрируют удивительно похожие паттерны быстро адаптирующихся и почти симметричных включенных и выключенных МТ-токов в ответ на приложенные механические нагрузки (см.8). В четырех классах, включая нейроны рецептора прикосновения (TRN), такие токи зависят от натрия и чувствительны к амилориду. Генетическая диссекция связывает эти токи MeT с DEG / ENaC (дегенерин / эпителиальный натриевый канал) белками в TRNs (9⇓⇓⇓-13) и мерцательным ноцицептором (14⇓-16). Транзиторный белок рецепторного потенциала выполняет роль механорецепторов пятого класса, которые функционируют как сенсор текстуры (9, 17–20). Оба типа ионных каналов также участвуют в ощущении прикосновения и боли у личинок Drosophila (9, 11, 14, 21–25).В совокупности эти наблюдения предполагают, что ни один класс белков не отвечает за формирование сенсорных каналов MeT и что свойства быстрой адаптации и симметричных ответов включения и выключения не связаны однозначно с одним классом канальных белков. Самое раннее понимание механизмов быстрой адаптации появилось в результате работы над тельцем Пачини у млекопитающих в 1960-х гг., В котором их быстрые и симметричные реакции были связаны с луковичной пластинчатой капсулой, которая покрывает его специализированное нервное окончание (9, 11–13, 19, 26⇓⇓ – 29).Было предложено, чтобы эта многослойная вспомогательная структура функционировала как чисто механический фильтр (14, 17, 30) или как механохимический фильтр, воплощенный в петле обратной связи, в которой считается, что ГАМКергические сигналы от ламеллярной капсулы подавляют потенциалы действия во время устойчивого стимула ( 12, 13, 16, 18, 20, 25, 28). Но быстро адаптирующиеся токи MeT обнаруживаются в других сенсорных афферентах млекопитающих, таких как те, которые, как считается, иннервируют тельца Мейснера и волосяные фолликулы (см. Ссылки 8, 31).Более того, все механорецепторные нейроны в C. elegans лишены дополнительных структур, аналогичных тельце Пачини, но они все же обнаруживают быструю адаптацию. Таким образом, быстро адаптирующиеся нейронные реакции не зависят от специализированных дополнительных структур. Быстрая адаптация может быть автономным и внутренним свойством каналов MeT или свойством системного уровня, которое зависит от организации таких каналов в их естественной среде. Piezo2 необходим для быстрой адаптации вызванных прикосновением токов в клетках Меркеля в фолликулах усов (32⇓ – 34) и приводит к быстро адаптирующимся, механически активируемым каналам при экспрессии в гетерологичных клетках (35, 36), наблюдения согласуются с внутренними или клеточно-автономными механизмы.Подобным образом и как отмечалось выше, каналы, зависящие от DEG / ENaC MeT белка MEC-4, быстро активируются и адаптируются к устойчивым механическим нагрузкам в своих естественных условиях (12, 37). В отличие от каналов Piezo2, однако, MEC-4-зависимые каналы являются конститутивно активными (26, 38), когда экспрессируются в гетерологичных клетках. Это последнее наблюдение согласуется с идеей, что механическая активация и динамика ее ответа отражают не только внутреннюю механочувствительность MeT каналов, но также механику системного уровня и свойства материала иннервируемой ткани. Мы рассудили, что усилия по различению внутренних механизмов и механизмов системного уровня будут ускорены с помощью инструментов, которые могут прикладывать механические нагрузки и измерять их влияние на деформацию тканей и ток через мембрану параллельно в условиях, которые поддерживают целостность всей сенсорной системы. . С этой целью мы разработали FALCON (приложение механических нагрузок с обратной связью в сочетании с нейрофизиологией in vivo), систему, которая сочетает управляемую с обратной связью механическую стимуляцию с записью патч-зажима целых клеток in vivo.Управление с обратной связью по усилию достигается с помощью настраиваемых чувствительных к усилию кремниевых микрокантилеверов со встроенными пьезорезистивными датчиками деформации (39⇓ – 41). Эта система может работать либо в зажиме смещения, обеспечивая определенные смещения при измерении приложенной силы, либо в зажиме усилия, создавая определенные силы при измерении приложенного смещения (32, 34, 42, 43). Как мы показываем здесь, полученные данные о приложенной механической силе, вдавливании тела и вызванных токах MeT позволяют детально исследовать физические параметры, которые управляют активацией TRN, а также проводить количественное физическое моделирование. Независимо от того, передают ли мы силу или смещение, системы механической стимуляции, используемые нами и другими для исследования токов MeT в C. elegans , не имеют контроля с обратной связью (12, 13, 16, 18, 20, 44). Подобные системы с разомкнутым контуром широко используются для анализа соматосенсорных нейронов млекопитающих (45, 46) и не могут различать изменения амплитуды стимула и адаптацию канала, независимо от того, представлены ли стимулы как приложенная сила или смещение стимулятора.FALCON обходит это ограничение, комбинируя механическую стимуляцию с замкнутым контуром с регистрацией мембранного тока in vivo целыми клетками (рис. 1 и рис. S1). Рис. 1.Быстрая адаптация не зависит от подачи стимула или метода рассечения. ( A ) Экспериментальная подготовка и интеграция с системой FALCON для одновременной механической стимуляции с обратной связью и записи патч-кламп. Минимальная диссекция обнажает только тело клетки переднего сенсорного рецептора (ALM) ( Left ), а препарат щелевого червя обнажает гонады, кишечник и тело клетки ALM ( Center ).На микрофотографии показано положение микрокантилевера относительно тела клетки ALM (, справа, ). ( B ) Схематическое изображение поперечного сечения тела червя и положения TRN относительно кутикулы, эпидермиса, мышцы стенки тела и микрокантилевера. ( C ) Подготовка щелевого червя снижает жесткость тела по сравнению с процедурой минимального рассечения (синий, n = 21 мягкий червь; красный, n = 4 жестких червя). Кривые показывают взаимосвязь между силой и вдавливанием отдельных червей.( D — F ) Следы репрезентативной силы ( F ), вдавливания ( z ) и мембранного тока ( I ) для записи в жестком червяке, вызванном одноступенчатым протоколом с принудительным зажимом ( D ) и в мягком червяке, вызванном одноступенчатым протоколом с принудительным зажимом ( E ) и зажимом смещения ( F ). Пунктирными линиями показаны де свертки ползучести вдавливания ( E , τ = 34 мс) и релаксации силы ( F , τ = 45 мс), наблюдаемых у мягких червей во время принудительного зажима и зажима смещением. записи соответственно.Аналогичные результаты были получены в общей сложности 2 и 21 записи от мягких червей, проанализированных при смещении и силовом зажиме, соответственно, и 4 записях от жестких червей, проанализированных при силовом зажиме. Каждая запись представляет собой среднее значение от 10 до 14 испытаний. Рис. S1.Схема для FALCON. Эта система обеспечивает одновременную управляемую с обратной связью доставку произвольных механических нагрузок с помощью самочувствительного пьезорезистивного кантилевера, интегрированного с оборудованием для регистрации in vivo целых клеток с помощью патч-клампа.( A ) Схема системы. ( B ) Жесткость и собственная частота (измеренные в воздухе) консолей, использованных в этом исследовании. ( C ) Схема системы управления схемой управления FALCON. Здесь мы используем эту систему, чтобы показать, что токи TRN MeT увеличиваются с вдавливанием тела, неприложенной силой и со скоростью стимуляции, и мы разрабатываем механическую модель, которая воспроизводит основные динамические особенности активации тока MeT in vivo. РезультатыМеханические нагрузки вызывают быстро адаптирующиеся «включенные» и «выключенные» токи MeT независимо от режима доставки или жесткости ткани.Сначала мы спросили, как на текущую адаптацию MeT повлияли изменения в механике тела червя. Чтобы ответить на этот вопрос, мы подготовили червей, используя две процедуры вскрытия, стратегия, позволяющая нам сравнивать токи MeT в двух различных механических режимах. Первой процедурой была стандартная процедура рассечения с помощью щелевого червя, которая высвобождает часть гонад и кишечника, чтобы снизить внутреннее давление и облегчить успешное рассечение тел нейрональных клеток (10, 47). Второй — это недавно разработанная процедура вскрытия, которая лучше сохраняет физическую целостность нематоды, обнажая только интересующее тело нейрональной клетки (48–50) (рис.1 А ). Мы прикладывали механические нагрузки, совместив стеклянную микросферу, прикрепленную к кончику кантилевера, с верхней поверхностью животного, которая была его левой стороной (рис. 1 A и B ). В результате процедуры рассечения с помощью щелевого червя были получены черви, которые на ~ 60–90% мягче, чем те, которые были получены с помощью менее инвазивной процедуры рассечения (рис. 1 C ), которые имели среднюю эффективную жесткость 1,1 ± 0,3 Н / м ( среднее ± стандартное отклонение, n = 4). Это значение аналогично измеренным ранее для иммобилизованных или свободно перемещающихся интактных животных (12, 42, 51, 52).Для краткости мы называем червей, полученных с помощью щелевой червячной процедуры, «мягкими», а червей, полученных путем менее инвазивной диссекции, — «жесткими». Независимо от метода рассечения и жесткости тела (рис. 1 D и E ) или от того, подавались ли стимулы под действием силового зажима или смещения зажима (рис. 1. E и F ), токи MeT быстро адаптируются. и активируется в ответ на приложение и снятие механических нагрузок. Например, в записях, полученных от жестких и мягких червяков, подвергнутых большим механическим нагрузкам, связанным с усилием, средняя постоянная времени для адаптации тока MeT составляла 23 мс ( n = 2, F = 5 мкН) и 24 ± 11 мс. (среднее ± стандартное отклонение, n = 21, F = 1 мкН) соответственно.Средняя постоянная времени адаптации токов MeT, вызванных большими механическими нагрузками, ограниченными смещением, составляла 22 мс ( n = 2, мягкие червяки, x t = 5 мкм). Эти значения аналогичны тем, о которых сообщалось ранее при использовании методов механической стимуляции без обратной связи (12, 13, 44, 53). Важно отметить, что эти скорости адаптации отделены от скорости стимуляции, потому что время нарастания замкнутого контура было намного быстрее, чем адаптация тока MeT во всех случаях, варьируясь от 4 мс ( n = 2, жесткие черви под зажимом силы, F = От 5 мкН) до 6 ± 2 мс (среднее ± стандартное отклонение, n = 19, мягкие червяки под смещением зажима, F = 1 мкН) до 8 мс ( n = 2, мягкие червяки под смещением зажима, x t = 5 мкм).Эти наблюдения показывают, что быстрая адаптация сохраняется при механической стимуляции с обратной связью и при фундаментальном изменении основной механики тела методом рассечения. Динамика механики тела, однако, зависела от метода подготовки. У мягких червей вдавливание, необходимое для поддержания постоянной силы, увеличивается с течением времени, это механический процесс, известный как ползучесть (рис. 1 E , Middle ). Средняя постоянная времени для ползучести составляла 25 ± 11 мс (среднее ± стандартное отклонение, n = 21 запись от мягких червей) при F = 1 мкН, по оценке деконволюции ответа с профилем стимула ( методы ) .Усилие, необходимое для поддержания постоянного вдавливания, уменьшилось (ослабление силы; Рис.1 F , Top ) со средней постоянной времени 35 мс ( n = 2 мягких червяка, x t = 5 мкм). Однако ползучесть вдавливания не наблюдалась в записях от жестких червей (рис. 1 D ). Поскольку скорости адаптации тока MeT были одинаковыми как у жестких, так и у мягких червей, ползучесть вдавливания и релаксация сил, которые наблюдались только у мягких червей, не могут объяснить быструю адаптацию тока MeT. MeT Амплитуда тока зависит от вдавливания, неприложенной силы.Установив процедуры для анализа токов MeT в различных механических режимах, мы использовали эту манипуляцию, чтобы определить, увеличивается ли амплитуда тока MeT с приложенной силой или индуцированным вдавливанием. Концептуально мы полагаемся на тот факт, что данная сила связана с большим вдавливанием в мягких червях по сравнению с жесткими червями. Как показано на рис.2, мы обнаружили, что жесткий механический режим смещает среднюю точку кривых силы тока (I-F) в сторону более высоких сил ( F 1/2 = 3.0 мкН и 0,38 мкН для жестких и мягких червей соответственно), а также значительно снижает чувствительность к силе. (Наклоны δ F подогнанных кривых IF составляли 0,21 и 1,55 для мягких и жестких червяков, соответственно.) Напротив, средняя точка и наклон кривых (Iz) с отпечатком тока были неразличимы. между двумя механическими режимами. (Средние точки, z 1/2 , подобранных функций составляли 2,4 мкм и 2,9 мкм у жестких и мягких червей, соответственно, а наклоны δ z были равны 1.4 и 1.3 для мягких и жестких червей соответственно.) Таким образом, амплитуда тока MeT увеличивается пропорционально вдавливанию тела, а не приложенной силе. Этот результат согласуется с нашим недавним исследованием поведенческой чувствительности у C. elegans (42) и предполагает, что вероятность ответа на нежное прикосновение зависит от амплитуды тока MeT. Как отступы на теле могут активировать каналы MeT? Простая модель состоит в том, что вдавливание вызывает деформацию и что именно эта деформация служит проксимальным физическим стимулом для активации собственных каналов MeT внешними механическими нагрузками.Такая модель предсказывает, что каналы MeT чувствительны к скорости приложенного стимула. Ниже мы тестируем эту модель экспериментально, а также аналитически путем разработки физической модели. Рис. 2. ТокиMeT чувствительны к вдавливанию тела. ( A и B ) Следы силы ( F ), вдавливания ( z ) и тока ( I ) для записей от мягкого (синие следы) и жесткого (красные следы) червя, стимулированного под воздействием усилие зажима между 0.05 и 6 мкН. Аналогичные результаты получены в общей сложности на 21 мягком и 4 жестких червях. Каждая запись представляет собой среднее значение от 10 до 14 испытаний. ( C ) Пиковый ток увеличивается пропорционально силе, но зависимость кажущейся силы отличается у мягких ( n = 18, синий) и жестких ( n = 2, красный) червяков. ( D ) Пиковый ток увеличивается пропорционально вдавливанию как у мягких (синий), так и у жестких (красный) червяков. Данные взяты из тех же записей, что и в C . Плавные линии в C и D — это функции Больцмана, соответствующие данным; заштрихованная область показывает 95% доверительный интервал соответствия.Коэффициенты подбора для зависимости силы в C составляют F 1/2 , сила, необходимая для полумаксимальной активации, и δ F , наклон кривой, и имеют следующие значения: F 1/2 = 0,38 мкН и δ F = 2,13 для мягких червей; F 1/2 = 3,0 мкН и δ F = 1,55 для жестких червей. Коэффициенты подгонки для отступа в D равны z 1/2 , отступ, необходимый для полумаксимальной активации, и δ z , наклон кривой, и имеют следующие значения: z 1 / 2 = 2.9 мкм и δ z = 1,40 для мягких червей; z 1/2 = 2,4 мкм и δ z = 1,25 для жестких червей. Токи MeT активируются в ответ на быстрые, но не медленные механические стимулы.Затем мы спросили, как на активацию канала MeT влияет изменение скорости механической стимуляции. Мы разработали профили стимулов с постепенным нарастанием и удержанием, в которых фиксированное вдавливание производилось с переменной скоростью и быстро удалялось. Быстрое смещение обеспечивает положительный контроль наличия функциональных каналов MeT, тогда как переменная скорость начала проверяет чувствительность к скорости активации MeT.Мы обнаружили, что медленные линейные изменения не смогли активировать токи MeT, даже несмотря на то, что установившееся углубление, полученное в этих экспериментах, было достаточным, чтобы вызвать устойчивые отключенные токи одинаковой амплитуды во всех случаях (рис. 3 A ), предполагая, что, в отличие от Escherichia coli MscS (54, 55), эти каналы не инактивируются молча в ответ на низкоскоростную стимуляцию. Таким образом, TRN C. elegans и их MeT-каналы чувствительны к скорости стимуляции. Рис. 3.TRN C. elegans чувствительны к скорости и частоте стимула. ( A ) Сила ( F ), вдавливание ( z ) и ток ( I ), зарегистрированные в мягком червяке в ответ на стимулы ускорения и удержания, подаваемые под зажимом смещения ( n = 1 червь). ( B ) Регистрация силы, вдавливания и тока в мягком червяке в ответ на синусоидальные стимулы, подаваемые под действием зажима силы. Аналогичные результаты были получены в общей сложности в четырех записях от мягких червей.( C ) Спектры мощности токов, вызванных синусоидальными стимулами, приложенными к TRN в мягком червячном зажиме под действием силы. Выдающиеся пики на 6, 20 и 60 Гц соответствуют частотам стимула 3, 10 и 30 Гц соответственно и иллюстрируют, что TRN генерируют нелинейные сигналы, которые пропорциональны структуре динамических входов. ( D ) Чувствительность токов MeT в зависимости от частоты стимула. Чувствительность определяется как пиковая амплитуда тока, деленная на приложенную силу (от пика до пика) или достигнутое вдавливание, и имеет единицы пА / мкН (или пА / мкм) перед нормализацией к значению при максимальной приложенной частоте.Данные были объединены из четырех записей мягких червей, стимулированных принудительным зажимом на указанных частотах. Кроме того, мы определили реакцию на синусоидальные профили нагрузки, которые варьировались по частоте от 1 до 300 Гц и приложили силы, достигающие максимальной размах 1,96 ± 0,02 мкН (среднее ± стандартное отклонение, n = 4) при низкие частоты, но уменьшаются по амплитуде на высоких частотах (Рис. 3 B , Top ). В соответствии со скоростной зависимостью, наблюдаемой в ответ на стимулы с нарастанием и удержанием, стимулы, подаваемые на частотах менее 3 Гц, не вызывали какого-либо заметного изменения мембранного тока (рис.3 B , Нижняя ). Однако при 100 Гц значительно меньшая размах силы 0,45 ± 0,04 мкН (среднее ± стандартное отклонение, n = 4) давала устойчивый и устойчивый внутренний ток. На промежуточных частотах и размахе амплитуды ток MeT демонстрировал колебания значительной мощности на удвоенной частоте стимула (рис. 3 B и C ). Взятые вместе, эти результаты показывают, что TRN являются датчиками вибрации, нечувствительными к низкочастотной (<3 Гц) механической стимуляции (рис.3 D ). Биофизические модели симметричных и быстро адаптирующихся токов MeT.Охарактеризовав, как токи MeT реагируют на динамические механические нагрузки, мы использовали эти экспериментальные результаты для разработки механической модели, чтобы углубить наше понимание и ответить на вопросы о физике активации каналов MeT. Общие элементы модели показаны на рис. 4 A и B , а концептуальная и математическая формулировка физической модели подробно описана в методах и SI методах .Эвристически считается, что приложение механических нагрузок к коже вызывает зависящую от времени деформацию в вязкоупругих тканях, которые охватывают TRN, и гипотетический вентильный элемент связывает каналы MeT с этими вязкоупругими тканями. Для удобства мы называем стробирующий элемент филаментом и отметим, что роль, которую играет эта филамент, также может выполняться за счет взаимодействий между MeT-каналом и фосфолипидным бислоем. Дифференциальные смещения между MeT-каналами и их нитями приводят к удлинению волокон, которое пропорционально скорости вдавливания, и такое удлинение способствует открытию канала ( SI Methods ).Как только каналы MeT открываются, модель утверждает, что силы упругости и вязкости (трения) возвращают соединенные волокна в их расслабленную форму, закрывая каналы и обеспечивая быструю адаптацию. Эта модель предлагает объяснение быстрой адаптации, симметрии между реакциями включения и выключения (рис.1 C — E и 4 C и D ) и удвоением частоты в ответ на синусоидальные стимулы. (Рис.3 B и C ). Рис. 4.Реконструкция динамики отклика MeT-токов с помощью физической модели TRN как вязкоупругих механических фильтров. ( A ) Схема, показывающая силы, ортогональные оси вдавливания. ( B ) Схема, показывающая один из возможных вариантов реализации модели: канал MeT, связанный через эластичную нить с якорем (красный шар), который может перемещаться через вязкий внеклеточный матрикс. Система находится в состоянии покоя, и канал MeT закрыт на верхней и нижней панелях.Движение сверху по часовой стрелке: внутренние силы, возникающие в результате внешней деформации, вызывают поперечный сдвиг между внеклеточным матриксом и якорем, растягивая нить и активируя канал; вязкоупругие силы возвращают нить в ее расслабленную форму, что приводит к адаптации и последующему закрытию канала MeT; внутренние силы, возникающие при снятии внешней деформации, вызывают латеральный сдвиг внеклеточного матрикса и якоря, растягивая нить и активируя канал; наконец, вязкоупругие силы завершают цикл симметрично.( C ) Сравнение экспериментальной и теоретической реакции на механическую нагрузку, приложенную при силовом зажиме. Показаны (сверху вниз) измеренное вдавливание, прогнозируемые вероятности состояния канала MeT как функция времени во время стимуляции, измеренные (зеленый) и прогнозируемые макроскопические токи MeT (черный). Параметры модели SLS описаны в третьей строке таблицы S1. ( D ) Набор измеренных (зеленый) и прогнозируемых (черный) токов MeT, вызванных синусоидальными эпохами, выбранными из записей в мягком червяке.Параметры модели как в C . ( E ) Токи MeT, вызванные произвольным профилем стимула (зеленый), и отклик, предсказанный с использованием тех же параметров модели, что и в C и D (черный). Когда упругие и вязкие силы представлены обычно используемой стандартной линейной твердотельной моделью (SLS) (9, 11), модель точно предсказывает экспериментально наблюдаемые токи MeT, вызванные импульсными механическими стимулами у мягких червей (рис. 4 ). C и рис.S2). Поскольку модель также явно включает взаимосвязь между механическими нагрузками и средней вероятностью того, что каналы MeT будут закрыты или войдут в субпроводимость и полностью открытые состояния, ее также можно использовать для прогнозирования взаимосвязи между механическими нагрузками и состояниями каналов (рис. 4 C , Средний ). Временной масштаб и профиль прогнозируемых откликов адаптирующегося тока являются результатом как динамического взаимодействия трех основных состояний MEC-4-зависимого канала MeT — одного закрытого непроводящего состояния и двух открытых, проводящих состояний (14) — и вязкоупругого механические параметры модели (см. методы и SI методы ).В то время как моделирование включало открытые и закрытые состояния, они не включали неактивированные состояния, потому что они не были необходимы для учета адаптации MeT и не обнаруживались экспериментально. Затем мы бросили вызов модели, чтобы воспроизвести реакцию, генерируемую синусоидальными стимулами, и общий набор параметров в равной степени был способен предсказывать токи, вызванные этими более сложными профилями механической нагрузки (рис. 4 D ). Мы также спросили, может ли модель воспроизвести реакцию на произвольные профили стимулов, такие как показанный на рис.4 E . Тесное соответствие между предсказанным ответом (черный) и экспериментальными наблюдениями (зеленый) подчеркивает надежность модели. Рис. S2.Сравнение измеренных и смоделированных токов, вызванных множеством различных форм сигналов вдавливания. ( A ) Импульсы вдавливания. ( B ) Быстрые (, слева, ) и медленные (, справа, ) стимулы нарастания. ( C ) Синусоидальные стимулы 1–100 Гц. На каждой панели верхние кривые показывают профиль стимула, а нижние кривые показывают токи механорецепторов, измеренные при -60 мВ (темно-зеленый) и теоретический прогноз модели SLS (уравнение. S16 , черный). Пунктирными линиями показаны ожидаемые верхний и нижний пределы прогнозируемого тока, основанные на 1 SD, оцененном по формуле. S13 и типичное количество 25 активированных каналов. Эта запись (169) относится к мягкому червю и также показана на рис. S4 – S6. Единый набор оптимизированных параметров (см. Таблицы S1 и S2) воспроизводил совокупность данных, собранных от каждого мягкого червя (Рис. 4 и Рис. S2 и S3), открытие, которое предполагает, что свойства, которые определяют реакцию отдельного червя прикосновения фиксированы и не зависят от типа применяемого механического стимула.Чтобы дополнительно проверить эту идею, мы использовали оптимизированные параметры импульсных механических стимулов для предсказания синусоидальных стимулов, стимулов с линейным нарастанием и удержанием и произвольных стимулов, и мы обнаружили близкое соответствие между предсказанным ответом и экспериментальными наблюдениями (рис. S4). Кроме того, когда мы предсказали теоретический отклик для одного червя, используя параметры, оптимизированные для другого червя, мы обнаружили близкое общее согласие между ними (рис. S3). Таким образом, существует высокая степень согласованности между оптимальными наборами параметров модели для отдельных мягких червей, несмотря на различия в жесткости тела, возникающие во время процедуры вскрытия (рис.1 С ). Таблица S1.Оптимальные параметры, полученные при подгонке экспериментальных данных записи 169 к различным вязкоупругим моделям, представленным в тексте Таблица S2.Оптимальные параметры, полученные путем подгонки экспериментальных данных записи 173 к различным вязкоупругим моделям, представленным в тексте; Структура строк и обозначения такие же, как в Таблице S1 Рис. S3.Различия в теоретических предсказаниях, полученных на основе разных записей. ( A и C ) Формы сигналов стимула.( B и D ) Токи механорецепторов, измеренные при -60 мВ в записи 173 (темно-зеленый) по сравнению с предсказаниями модели SLS (уравнение S16 ) с использованием оптимальных параметров для записи 173 (черный, вверху, модель 173) и полученные из оптимальных параметров записи 169 (ярко-зеленый, внизу, модель 173). В то время как прогнозы, полученные на основе оптимальных параметров для самой записи 173, явно имеют более высокое качество, общее поведение согласуется даже с параметрами, оптимизированными для другой записи 169.Эта запись (173) сделана мягким червем и также показана на рис. S7. Рис. S4.Прогнозы с параметрами модели, полученными из реакции на импульсы вдавливания, воспроизводят реакцию на более сложные формы волн стимуляции. ( A ) Синусоидальные стимулы ( верхний ), вызванные токи (темно-зеленый, нижний ) и прогнозируемый ответ (черный, нижний ). ( B ) Стимул нарастания и удержания (, верх, ), вызванные токи (темно-зеленый, , нижний ) и прогнозируемая реакция (черный, , нижний ).( C ) Произвольный профиль стимула (, верх, ), вызванные токи (темно-зеленый, , нижний ) и прогнозируемый ответ (черный, , нижний ). Экспериментальные данные взяты из записи 169, которая также показана на рис. S2, S5 и S6. Наши теоретические прогнозы также устойчивы в отношении некоторых деталей моделирования. Так называемая модель Кельвина, модель SLS в пределе исчезающей памяти о силе трения (9), уже в значительной степени отражает отклик канала MeT (рис.S5 – S7). Кроме того, хотя три состояния канала (закрытый, полностью открытый и субпроводимость) были введены для согласования экспериментальных наблюдений каналов, содержащих MEC-4 (14), токи MeT уже хорошо воспроизводятся более простой моделью с двумя состояниями, включающей одно закрытое и одно открытое состояние (рис. S6 и S7). В частности, конститутивная активность, наблюдаемая на фиг. 3 B или 4 D на высоких частотах синусоидальной стимуляции присутствует в обеих моделях. Действительно, при высокой частоте стимула переходы между различными конформационными состояниями больше не следуют входному стимулу (рис.S6 и S7), а инерция каналов MeT делает состояния заселенными примерно постоянными долями. Рис. S5.Сравнение токов механорецепторов с прогнозами, полученными на основе различных моделей. ( A ) Формы сигналов стимула, применяемые с помощью FALCON. ( B ) Токи механорецепторов, измеренные при -60 мВ (темно-зеленый), по сравнению с прогнозами, полученными на основе вязкоупругих моделей, обсуждаемых в основном тексте. Прогнозы, полученные с использованием модели SLS (уравнение S16, , черный), очень похожи на предсказания, данные моделью, включающей производные вдавливания более высокого порядка (уравнение. S18 , пурпурный). Улучшение совпадения экспериментальных трасс и прогнозов отражает лучшее описание быстрых изменений в динамике. Экспериментальные данные взяты из записи 169, которая также показана на рис. S2, S4 и S6. Рис. S6.Прогнозы, полученные на основе модели Кельвина (уравнение S2 ) с двумя или тремя конформационными состояниями для каналов MeT (запись 169). ( A ) Формы сигналов стимула, применяемые с помощью FALCON. ( B ) Токи механорецепторов, измеренные при -60 мВ (темно-зеленый), и прогнозы, полученные на основе модели Кельвина (уравнение. S4 ) с двумя конформационными состояниями (открытое и закрытое) и тремя конформационными состояниями (открытое, субпроводящее, закрытое) в пурпурном и черном цветах соответственно. Экспериментальные данные взяты из записи 169, которая также показана на рис. S2, S4 и S5. Рис. S7.Прогнозы, полученные на основе модели Кельвина (уравнение S4 ) с двумя или тремя конформационными состояниями для каналов MeT (запись 173). ( A ) Формы сигналов стимула, применяемые с помощью FALCON. ( B ) Токи механорецепторов, измеренные при -60 мВ (темно-зеленый), и прогнозы, полученные на основе модели Кельвина (уравнение. S4 ) с двумя конформационными состояниями (открытое и закрытое) и тремя конформационными состояниями (открытое, субпроводящее, закрытое) в пурпурном и черном цветах соответственно. Экспериментальные данные взяты из записи 169, которая также показана на рис. S3. Полоса пропускания FALCON была ограничена необходимостью вручную настраивать коэффициенты усиления контроллера для оптимальной доставки заданного стимула и сложностью перенастройки во время записи ( методы ). Это ограничение помешало нам полностью исследовать диапазон частотной характеристики C.elegans TRN и экспериментального тестирования того, ведет ли вся система себя больше как высокочастотный или полосовой механический фильтр. Тем не менее, поскольку физическая модель близко соответствует имеющимся экспериментальным данным (рис. 4 и 5), мы можем использовать модель для размышлений о механическом фильтре, который формирует отклик C. elegans TRN на изменяющиеся во времени синусоидальные механические нагрузки. (т.е. вибрация). Общие соображения относительно пассивных вязкоупругих материалов предполагают, что сила, необходимая для создания вдавливания кутикулы фиксированной амплитуды, должна увеличиваться с частотой на высоких частотах (9, 12, 13, 19, 26, 28).В этом сценарии ожидается, что амплитуда образовавшихся вмятин будет уменьшаться по мере увеличения их частоты. Это уменьшение амплитуды вдавливания в сочетании с неспособностью медленно движущихся стимулов активировать токи могло бы вызвать отклик полосового фильтра. Рис. 5 A показывает экспериментальные результаты вместе с моделями, основанными на этом сценарии. В моделировании, но не в экспериментах, мы также можем задаться вопросом, как вся механическая система работает в условиях, в которых приложенная максимальная сила не зависит от частоты стимула.Как показано на Рис. 5 B , этот анализ показывает, что вдавливание уменьшается с частотой и что пиковый ток и чувствительность этого препарата достигают максимальных значений при 150 и 725 Гц соответственно. Моделирование также показывает, что ток колеблется в два раза выше входной частоты и что амплитуда таких колебаний уменьшается с частотой (Рис. 5 C ). Одна из моделей, объясняющих это наблюдение, заключается в том, что на высоких частотах каналы находятся в открытых состояниях и редко посещают закрытые состояния.Мы отмечаем, что эти рассуждения о механической фильтрации у мягких животных не принимают во внимание различия в жесткости тела среди людей или активные механизмы модуляции жесткости тела во время сенсорных стимулов, которые наблюдались у других животных (например, ссылка 30) и которые могли бы обеспечивают механизмы на уровне организма для регулирования частотной зависимости ощущения прикосновения. Рис. 5.Экспериментально-вычислительное исследование АЧХ тактильных ощущений у мягких животных.( A ) Моделирование с использованием параметров, оптимизированных для соответствия ответам на механические стимулы (рис. 4), воспроизводит экспериментальные ответы на синусоидальные стимулы в репрезентативной записи от мягкого червя. В таблице S1 (третья строка) перечислены параметры для модели SLS. Показаны (сверху вниз) приложенная сила (от пика к пику), результирующее вдавливание (от пика к пику), пиковый ток и чувствительность (пА / мкм). Сплошные черные линии показывают экспериментальные результаты репрезентативной записи; сплошные синие линии показывают результаты, объединенные по четырем записям; пунктирные черные линии показывают моделирование; а заштрихованные области указывают на ошибки измерения и моделирования.Приложенная сила уменьшается с частотой из-за ограничений устройства FALCON. ( B ) Моделирование механической и физиологической реакции на приложенную силу до 3 кГц. Параметры модели как в A . Показаны (сверху вниз) приложенная сила (пик), результирующая вмятина (пик), пиковый ток и чувствительность (пА / мкм). Вдавливание уменьшается с частотой в результате свойств механической системы, несмотря на постоянную амплитуду приложенной силы. ( C ) Моделирование вдавливания и токов, вызванных синусоидальными силовыми стимулами.Параметры модели такие же, как у A и B . Экспериментально установлено, что частота колебаний тока примерно в два раза превышает частоту стимула, за исключением высоких частот, когда большие колебания тока уменьшаются. ОбсуждениеПредставленная здесь динамика ответа характерна для других быстро адаптирующихся механосенсорных нейронов, включая ноцицепторов C. elegans и Drosophila (12, 13, 16, 18, 20, 25) и нейронов, иннервирующих пачиниан и Тельца Мейснера и волосяные фолликулы у млекопитающих (см.31, 56). Тот факт, что сходная динамика ответа обнаруживается в типах и в сенсорных нейронах, которые радикально различаются по своей морфологии, убедительно свидетельствует о том, что это свойство возникает из общего физического механизма. Важно отметить, что представленная и проверенная здесь модель требует только канала, который реагирует и адаптируется к окружающей среде посредством вязкоупругой динамики. Несколько молекулярных вариантов осуществления совместимы с нашей моделью, например, одиночные или множественные эластичные нити, привязанные непосредственно к каналу MeT или к структуре, которая перекрывает путь проникновения ионов, который отодвигается латерально деформациями кожи.Более того, такие филаменты могут быть прикреплены к внеклеточному матриксу или к цитоскелету. В настоящее время экспериментальные данные делают маловероятной прямую связь между каналом MeT и цитоскелетом микротрубочек в TRN (32, 34). Однако такая связь была предложена и охарактеризована для колоколообразных сенсилл у взрослых особей Drosophila, и мультидендритных ноцицепторов у личинок (35, 57). Наконец, предлагаемая нами вязкоупругая динамика может возникать из самой плазматической мембраны, что предполагает, что белковая привязка к каналу MeT может не быть необходимым элементом для стробирования в физиологических условиях.Наша модель совместима с этой моделью «силы от липидов» (37). Выявление микроскопической и молекулярной природы механического устройства потребует целенаправленных экспериментов для идентификации вязкоупругих элементов и определения того, как такие элементы взаимодействуют с MeT-каналами на месте. Представленные здесь данные и методы предоставляют инструменты для манипулирования ключевыми белками и наблюдения за их влиянием на механику и адаптацию. Предлагаемый нами механизм устанавливает неожиданную связь между двумя различными механическими чувствами: осязанием и слухом.Система эластичных волокон напоминает аналогичные модели, первоначально предложенные для волосковых клеток (26), хотя и с одним существенным отличием. Быстро адаптирующиеся афференты симметрично реагируют на прикосновение как в начале, так и в момент смещения стимула (рис. 1 C — E и 4 C ). И наоборот, реакция волосковых клеток асимметрична по отношению к приложению силы, например, ответы наблюдаются только в начале стимуляции, указывающей на киноцилий пучка волос.Асимметрия обусловлена контролируемой геометрией звеньев кончика и менее выражена в незрелых волосковых клетках, когда присутствует несколько звеньев кончика, а их направления все еще ориентированы случайным образом (39). Симметрия, наблюдаемая в TRN C. elegans , по прогнозам, возникает из-за механики вдавливания тонкой кутикулы и последующей деформации филаментов, которая возникает как в начале, так и при смещении стимуляции в противоположных направлениях, но со сравнимыми амплитудами. Однако остается открытым вопрос, сохраняется ли симметрия на уровне отдельных каналов MeT или она сохраняется только на уровне всего механорецепторного нейрона.Для схемы, показанной на рис. 4, отдельные каналы MeT будут показывать симметричные отклики включения-выключения, если, например, прикрепление нити к каналу может скользить по окружности канала. Тогда эта система будет по существу аналогична люку, перекрывающему канал и скользящему вбок при механической стимуляции. И наоборот, если бы точка прикрепления нитей была фиксированной, отдельные каналы MeT имели бы предпочтение в направлении стимуляции, а симметрия включения-выключения была бы макроскопическим свойством всего нейрона из-за случайного положения каналов и их предполагаемые филаменты вдоль нейрита (32, 34).Таким образом, в отсутствие структур, нарушающих симметрию, таких как те, что встречаются в волосковых клетках позвоночных, щетине насекомых или остевых волосах млекопитающих (28, 58), мы ожидаем, что системы, характеризующиеся соматосенсорными нейронами, встроенными в тонкие ткани, обычно будут включать и выключать симметрия в их сенсорных реакциях. Как C. elegans может использовать чувствительность к деформации, скорости и вибрации? Давно известно, что C. elegans TRN участвуют в распознавании как нежного прикосновения к телу, так и нелокализованных механических нажатий (см.45). Черви меняют направление в ответ на переднее прикосновение, поведение избегания, которое позволяет им убегать от хищных грибов (47). Наши результаты показывают, что устойчивый ответ от C. elegans TRN требует краткого контакта с достаточной глубиной вдавливания. Этот временной и пространственный порог может гарантировать, что TRN не будут интерпретировать мелкие частицы, такие как бактерии, как отвращающие и уйти от потенциального источника пищи. Фильтрация низких частот также может позволить TRN игнорировать движения тела, которые включают частоты волнистости порядка 0.5 Гц при ползании по стандартным пластинам роста без еды (например, ссылки 48, 50). Таким образом, тонкая настройка системы может помочь TRN сосредоточиться на ответе на отталкивающие механические стимулы, оставляя при этом стимулы, такие как те, которые производятся структурой субстрата и самодвижением, другим нейронам механорецептора. МетодыШтаммы и культура нематод.Синхронизированные по возрасту нематод C. elegans выращивали на стандартных планшетах для выращивания OP50 при 20–22 ° C. Черви дикого типа представляли собой TU2769 [P mec-17 (uIs31) III ], интегрированный штамм, который использует промотор mec-17 для экспрессии GFP исключительно в TRN, которые проходят вдоль тела нематоды, как описано ранее. (12). Электрофизиология.Червей иммобилизовали на тонких подушечках из агарозы (2% вес / объем во внеклеточном солевом растворе) с помощью WormGlu (GluStitch). Наблюдения проводились на микроскопе Nikon Eclipse FN1, оснащенном оптикой Nomarski-DIC, водно-иммерсионным объективом 60 × / 1.0 N.A. и черно-белой камерой CCD (JAI CV-A55IR C). В большинстве экспериментов большая часть гонады и кишечника позади вульвы иссекалась для снятия внутреннего давления, как описано ранее (10).В некоторых экспериментах гонады и кишечник оставались на месте, как описано в ссылке. 49. Во всех экспериментах делали небольшой разрез непосредственно перед клеточным телом переднего нейрона рецептора прикосновения, ALM. Все разрезы были выполнены с использованием острого стеклянного инструмента для рассечения, установленного на гидравлическом манипуляторе (Narishige MMO-203). Тело клетки и задний нейрит ALM остались нетронутыми и на месте, что подтверждается просмотром флуоресценции GFP. Насосы через глотку и движения головы использовались для определения того, что черви были живы во время записи.Все записи были получены от нейрона ALM на левой стороне тела со стимулирующим кантилевером, расположенным сразу после луковицы глотки, на расстоянии ∼150 мкм от тела клетки (рис. 1 A ). Другие нейроны сенсорных рецепторов были недоступны из-за геометрических ограничений, налагаемых положением стимулирующего кантилевера и записывающей головки с фиксатором. Регистрирующие пипетки вытягивали из боросиликатного стекла до диаметра кончика 2–4 мм на съемнике для микропипеток P-97 (Sutter Instruments) и формировали путем полировки под давлением (59, 60).Пипетки имели сопротивление 6-17 МОм при заполнении физиологическим раствором (см. Ниже) и 20 мМ сульфородамина 101 (Invitrogen). Ток и напряжение мембраны были усилены и получены с помощью усилителя EPC-10 и программного обеспечения Patchmaster (HEKA Instruments / Harvard Biosciences). Аналоговые данные оцифровывались с частотой 10 кГц и фильтровались с частотой 2,9 кГц. Регистрация целых клеток была достигнута комбинацией всасывания и короткого импульса напряжения («zap»), где успех был подтвержден путем мониторинга диффузии GFP в пипетку и сульфородамина-101 в тело клетки. Внешний солевой раствор состоял из (в мМ): NaCl (145), KCl (5), MgCl 2 (5), CaCl 2 (1) и Hepes (10), pH доведен до 7,2 с помощью КОН. . Осмолярность всех внешних растворов доводили до ~ 325 мОсм с помощью 20 мМ D -глюкозы. Внутренний солевой раствор состоял из (в мМ): K-глюконат (125), KCl (18), NaCl (4), MgCl 2 (1), CaCl 2 (0,6), Hepes (1) и EGTA. (10), pH доводили до 7,2 с помощью КОН. Осмолярность внутриклеточных растворов составляла ~ 315 мОсм.Все химические вещества были закуплены у Sigma. СОКОЛ.Система FALCON сочетает в себе электрофизиологию патч-зажима с системой зажима-зажима. Система «усилие-зажим» похожа на системы, которые использовались ранее для характеристики механики тела и поведенческих реакций на прикосновение (5–7, 33, 36, 42, 43, 51, 52). Он обеспечивает управляемую обратной связью доставку заданных пользователем сил (или смещений) и состоит из пьезорезистивного кремниевого кантилевера, пьезоэлектрического привода со встроенным датчиком смещения тензодатчика (P-841.10, Physik Instrumente), и контроллер реального времени (National Instruments, программируемая вентильная матрица Compact Rio). Кантилеверы (ширина 30 мкм, длина 750 мкм, толщина 7 мкм) были изготовлены на микроорганизмах, как сообщалось ранее (8, 12, 40, 41, 43). Пьезорезистор служит встроенным тензодатчиком для измерения прогиба кантилевера; отклонение преобразуется в силу на основе калиброванной жесткости консольной пружины k c . Консоли приклеивались к печатным платам (ширина 5 мм, длина 29 мм, 0.Толщиной 8 мм) с эпоксидной смолой (Devcon) и подключается к измерительной цепи через алюминиевые провода. В ходе этих экспериментов использовались пять кантилеверов, которые имели значения k c от 0,773 до 0,868 Н / м и резонансные частоты в воздухе от 15,2 до 16,2 кГц (рис. S1 B ). Стеклянные микросферы (боросиликатное стекло диаметром 10 ± 1 мкм, ThermoFisher Scientific) прикрепляли к наконечникам кантилевера с помощью фотоотверждаемого акрилового клея (Loctite 352, Henkel) для создания определенной контактной поверхности.Наконец, алюминиевые проволочные соединения были покрыты эпоксидной смолой (Devcon), а затем 600 нм Parylene N (Specialty Coating Systems) были нанесены на каждое устройство. Этот последний шаг защищает электрические компоненты от воздействия физиологического раствора во время экспериментов. Печатная плата была изготовлена из FR4 (модуль Юнга = 11 ГПа) и была на несколько порядков жестче кантилеверов ( k PCB = 300 Н / м). Схема измерения состояла из консольного пьезорезистора, подключенного по схеме моста Уитстона, с двумя потенциометрами и резистором температурной компенсации.Смещение моста было установлено на 2 В, а его выход усилен в 1000 раз с помощью инструментального усилителя (INA103). Пьезорезистивные кантилеверы крепились к пьезоэлектрическому приводу под углом 10 °. Поскольку устройство помещалось непосредственно над поверхностью червя перед каждым экспериментом, глубина вдавливания образца ( z ) была рассчитана как z = x t — x c , где x t — это полное смещение привода, измеренное встроенным датчиком на приводе, а x c — отклонение кантилевера, измеренное пьезорезистором. Контроллер реального времени рассчитал и отрегулировал управляющее напряжение пьезоэлектрического привода, чтобы исправить ошибку между сигналом напряжения от пьезорезистивного кантилевера и желаемой уставкой. Обратная связь осуществлялась через контур управления, работающий на частоте 100 кГц. Контроллер был подключен к усилителю EPC-10 через систему цифрового ввода CompactRio и запускался цифровым сигналом от программного обеспечения Patchmaster (Harvard Bioscience) со временем задержки менее 2 мкс.Эта схема гарантировала, что система управления вырабатывала соответствующее командное напряжение привода для желаемого расстояния перемещения привода и приложенной силы. Система была откалибрована путем вдавливания предметного стекла и проверки выходного напряжения. Перед каждым экспериментом зонд располагался вне контакта с червем, мост Уитстона был сбалансирован, а усиление обратной связи регулировалось вручную для достижения самого быстрого времени нарастания с минимальным выбросом стимула в начале протокола стимуляции. Анализ данных.Емкость всей ячейки и последовательное сопротивление измеряли, как описано ранее (10, 12, 13, 38). Последовательное сопротивление не компенсировалось, а мембранное напряжение корректировалось с учетом потенциалов жидкого перехода, но не с учетом ошибок, возникающих из-за нескомпенсированного последовательного сопротивления. Анализ данных выполнялся с помощью Igor Pro (Wavemetrics) и MATLAB (MathWorks). Из-за дрожания во времени доставки импульсов механического стимула было необходимо согласовать реплики постфактум и перед усреднением ответов на предъявление стимулов.Выравнивание было достигнуто путем максимизации взаимной корреляции между небольшими регионами в одной реплике и идентичными регионами внутри каждой из других реплик (всего 6-14 повторов в типичной серии). После правильного выравнивания усреднялись данные о силе, смещении и токе мембраны. Чтобы оценить постоянные времени для активации и затухания канала MeT, мы аппроксимируем усредненные формы сигналов тока функцией I (t) = Gmax * (exp (-t / τ2) −exp (-t / τ1)) * (Vh − ENa ) + Io, , где G max — расчетная максимальная проводимость, V h — удерживающий потенциал, E Na — потенциал Nernst + для Na ионов в наших растворах, I o — базовый ток, а τ 1 и τ 2 — постоянные времени активации и адаптации соответственно.Спад приложенной силы, наблюдаемый при смещении зажима, описывался одной экспонентой. Повышение вдавливания или ползучесть, наблюдаемое при стимуляции мягких червей под действием зажима с усилием, соответствовало двойной экспоненте, где первая постоянная времени представляла скорость приложения стимула, а вторая постоянная времени представляла скорость ползучести. Нормы были усреднены для одного большого стимула (1 мкН для мягких червей с принудительным зажимом, 5 мкм для мягких червей с принудительным зажимом и 5 мкН для жестких червей с принудительным зажимом). Чтобы определить, как ток зависит от приложенной силы и вдавливания, пиковый ток был построен как функция силы или вдавливания, и полученные кривые были подогнаны с помощью функции Больцмана f (x) = Imax / (1 + exp ((X50-x ) / δ)), , где I max — расчетный максимальный ток мембраны, X 50 — расчетная половина максимального усилия или вдавливания, а δ — наклон, который контролирует крутизну кривой. . Затем данные были нормализованы к прогнозируемому I max и объединены по записям, полученным в аналогичных условиях в отношении процедуры вскрытия (жесткая, мягкая). Чтобы оценить скорость ползучести вдавливания в мягких червях, мы деконволюционировали временной ход вдавливания с временным ходом приложенной силы. Чтобы соответствовать диапазону вдавливаний, создаваемых для силы 1 мкН, мы ввели нелинейность, которая увеличивается с вдавливанием (15, 16, 40, 41). Точно так же, чтобы оценить скорость релаксации силы в мягких червях, мы деконволюционировали график силы во времени с примененным курсом времени вдавливания. Средние значения везде представлены как среднее ± стандартное отклонение. Статистический анализ выполнен с помощью IgorPro (Wavemetrics). Моделирование активации каналов MeT.Здесь мы описываем физические составляющие модели, разработанной для анализа и прогнозирования реакции TRN C. elegans; математическая формулировка модели подробно описана в SI Methods . Мы предположили, что каждый канал MeT в плазматической мембране TRN связан с механическими единицами (называемыми для простоты «якорями») через эластичные нити (рис. 4 B ). На рис. 4 B нить и якорь встроены во внеклеточный матрикс, но аналогичные результаты были бы получены, если бы эти элементы были встроены в другое место.Когда поверхность нематоды деформируется, в кутикуле возникает деформация (рис. 4 A ), и мы ожидаем, что такая деформация вызовет дифференциальные смещения между каналами и их якорями. Тонкость кутикулы (по сравнению с ее латеральным протяжением) диктует, что деформация, возникающая в результате вдавливания, перпендикулярного поверхности червя, наиболее сильна в тангенциальной плоскости (17⇓⇓ – 20, 42, 43). В результате эластичные нити вытянуты в противоположных направлениях, но с примерно симметричными амплитудами в начале и смещении стимула на поверхности нематоды (рис.4 A и B ). Две дополнительные силы определяют динамику систем нить / якорь: (–) сила Гука, возникающая в результате удлинения упругой нити, которая стремится восстановить расстояние релаксации нити; и ( ii ) силы трения между внеклеточным матриксом и системой филамент / якорь, которые сопротивляются их относительному движению. Мы представили комбинацию сил упругости и трения с моделями, обычно используемыми для вязкоупругих материалов (9, 11–13, 16, 18, 20–25, 44).В частности, модели Кельвина и SLS дают уравнения и результаты, представленные в основном тексте и в SI Methods . Модель Кельвина содержит пружину, установленную параллельно приборной панели, тогда как модель SLS содержит пружину, параллельную модулю Максвелла, который сам является еще одной пружиной, соединенной последовательно с приборной панелью (9, 11, 27, 29, 46). Кроме того, мы предположили, что активация каналов MeT следует за функцией Больцмана от удлинения их связанных нитей.Предыдущие экспериментальные наблюдения показали, что каналы MeT, содержащие MEC-4, принимают несколько открытых и закрытых состояний, включая заметное состояние субпроводимости (10, 14, 17). Следовательно, мы предположили, что каналы переходят между своими закрытыми и открытыми состояниями через третью конформацию с промежуточной проводимостью и что скорости переходов между этими конформационными состояниями соблюдают детальный баланс. Как подробно описано в SI Methods , допущения позволяют использовать экспериментальные профили вдавливания в качестве входных данных для получения прогнозируемых токов MeT.Затем мы сравнили экспериментальные кривые, чтобы они соответствовали параметрам нашей модели, и получили результаты, представленные здесь. SI МетодыКоличественная модель активации механорецепторных токов in vivo и ее приложение к сенсорному ощущению.Мы разработали теоретическую модель, которая связывает внешние нагрузки с активацией каналов MeT в нейронах рецептора касания C. elegans . Концептуальная основа этой модели представлена в основном тексте; здесь мы разрабатываем аналитическую и вычислительную основу модели и обсуждаем, как она была получена, реализована и использована для восстановления экспериментальных результатов.Вкратце, модель предполагает, что вдавливание тела вызывает боковую деформацию в теле червя, которая передается в каналы MeT посредством упругой нити, и что натяжение в упругой нити контролирует вероятность открытия канала. Локальный механический стимул активирует несколько каналов, распределенных по длине сенсорного нейрона, так что их вероятность открытия зависит от расстояния между каждым каналом и местом стимула. Как обсуждается ниже, мы использовали приближение среднего поля для упрощения модели с учетом влияния расстояния от точки контакта.Для конкретности мы сосредоточимся на конкретной микроскопической модели, в которой каналы связаны с якорем во внеклеточном матриксе. Отметим, однако, что наши результаты являются общими и совместимы с другими микроскопическими возможностями, такими как якоря в цитоскелете или искажение плазматической мембраны без какого-либо якоря, действующего как механический преобразователь. Динамика нити канал – якорь.Мы утверждаем, что каждый канал MeT через эластичную нить соединен с механическим узлом, который мы называем «якорем».«Приложение силы к поверхности C. elegans создает углубление глубиной ζ (t) и деформирует его кутикулу, которую мы рассматриваем как вязкоупругую среду. Учитывая, что кутикула представляет собой тонкую оболочку, следует, что доминирующая составляющая упругого напряжения возникает в плоскости, ортогональной отпечатку при умеренных деформациях (19). При больших деформациях доминирующий компонент напряжения остается локализованным в плоскости, локально касательной к поверхности червяка, которая изменяется, хотя при движении по поверхности (61).Мы ожидаем, что каналы MeT и их якоря будут смещены относительно друг друга в результате их различных вязкоупругих свойств. Эластичные нити, соединяющие каналы MeT с якорем, удлинены, что, как мы предполагаем, увеличивает вероятность того, что каналы войдут в свою открытую (проводящую) конформацию и приведут к значительным токам механорецепторов, как описано ниже. В частности, мы используем Xc, a для обозначения положения канала и анкера в отсутствие какой-либо деформации, xc, a (t) для обозначения их соответствующих смещений (которые зависят от исходных положений Xc, a) и S (X, t), чтобы указать смещение общей точки X в вязкоупругой среде, в которую встроен якорь.расстояния между каналом и якорем, которое предполагается постоянным на протяжении всего цикла стимуляции. Если направление изменится быстро, чего не будет в дальнейшем, потребуется многомерное описание динамики. В нижеследующем описании только первый член в разложении уравнения S1 достаточно, т. Е. Пружина гуковская, а сила упругости пропорциональна удлинению. Мы рассмотрели нелинейные члены в уравнении. S1 , и они не оказывают существенного влияния на результаты, представленные ниже. Под действием пружины анкер перемещается относительно вязкоупругой среды, в которую он встроен. Их относительному движению противодействует сила трения ℱ, которая в простейшем приближении принимает вид = −γd (xa − S (X ′, t)) dt≃ − γd (xa − S (Xa, t)) dt. [ S2] Здесь Xa + xa = X ‘+ S (X’, t), то есть X ‘- недеформированное положение той точки в вязкоупругой среде, которая находится в текущем местоположении якоря Xa + xa (t).Для второго приблизительного равенства мы предполагаем, что дифференциальное смещение между каналом и анкером невелико по сравнению с типичным масштабом изменения длины S . Ожидается, что порядок величины последнего будет аналогичен радиусу вдавливающего шарика и толщине кутикулы, которая составляет микрометры для рассматриваемой здесь ситуации. Разница в формуле. S2 выше переписывается как xa (t) −xc (t) + xc (t) −S (Xa, t) ≃x (t) −χ (Xa) ζ (t), [S3], где x = xa− xc, дифференциальное смещение S (Xa, t) −xc (t) размерно пропорционально отступу ζ (t), а функция χ (Xa) зависит от положения покоя Xa (должным образом безразмерного).Чтобы упростить обозначения, мы опускаем дополнительные зависимости × от фиксированных параметров, таких как размер и форма вдавливающего тела, внутреннее давление недеформированного червяка, вязкоупругие параметры и т. Д., И мы предполагаем, что для уравнения. S4 ниже, основная составляющая временной зависимости хорошо улавливается линейным членом ζ (t). Эффектом инерции обычно можно пренебречь в микроскопическом молекулярном мире, и обычно справедливо приближение сверхзатухания (62), которое влечет за собой приравнивание к нулю суммы сил.Используя уравнения. S1 — S3 , таким образом, окончательно получаем уравнение удлинения x = xa − xc: dxdt + 1τx = χdζ (t) dt, [S4], где τ = γ / k. Левая часть в уравнении. S4 описывает действие пружины параллельно с дроссельной заслонкой, которая известна как вязкоупругий модуль Кельвина (9, 11). Этого простого модуля уже достаточно, чтобы зафиксировать две основные особенности экспериментальных данных, представленных в основном тексте (рис. 1 и 2). Во-первых, внешнее вдавливание заставляет нить растягиваться пропорционально (dζ (t)) / dt, т.е.е., к производной отпечатка по времени. Таким образом, постоянное вдавливание не приведет к растяжению нити, тогда как резкое изменение вдавливания приведет к растяжению нити, которая затем расслабится из-за вязкоупругого комбинированного действия пружины и члена трения в формуле. S4 . Поскольку открытие каналов контролируется растяжением нити накала (см. Следующий раздел), модель естественным образом приводит к свойству адаптации, как показано на рис. 1 и 2. Кроме того, при приложении к поверхности силы C.elegans или облегчено, отступ (dζ (t)) / dt будет обратным, и x (t) изменит знак, но его модуль будет примерно таким же. Как мы подробно обсудим в следующем разделе, это свойство составляет основу симметрии в реакции на быстрое приложение и снятие механических нагрузок. Наконец, мы показываем в Сравнение с экспериментальными данными ниже, что уравнение простой модели. S4 (в сочетании с динамикой каналов, обсуждаемой в следующем разделе) выходит за рамки качественных аспектов отклика и также охватывает основные количественные аспекты. Б. Динамика стробирования каналов MeT.Ниже мы развиваем количественную зависимость между удлинением x в уравнении. S4 и вероятность того, что каналы находятся в открытых (проводящих) состояниях. MEC-4-зависимые каналы, ответственные за механорецепторные токи в рецепторах прикосновения, могут занимать закрытые, полностью открытые и промежуточные или субпроводящие состояния (14). Для простоты мы рассматриваем одно состояние субпроводимости и отмечаем, что этот подход обеспечивает отличную реконструкцию экспериментальных данных.Pc, Ps и Po — вероятности нахождения в закрытом, субпроводящем или открытом состоянии соответственно; Rji — это скорость перехода из состояния j в состояние i . Тогда динамика конформации канала определяется выражением {dPcdt = −Pc Rcs + Ps Rsc, dPsdt = Pc Rcs − Ps (Rsc + Rso) + Po Ros, dPodt = Ps Rso − Po Ros. [S5] Предполагая, что каналы соответствуют законам статистической физики равновесия, отношение двух вероятностей в состоянии равновесия Pieq и Pjeq задается фактором Больцмана Pieq / Pjeq = exp [−βΔGij], где ΔGij = Gi − Gj — разность свободной энергии между состояния i и j , β = 1 / kBT, T — термодинамическая температура, kB — постоянная Больцмана (см.г., исх. 62). Отсюда следует, что скорости перехода удовлетворяют соотношениям RcsRsc = e − βΔGsc, RsoRos = e − βΔGos. [S6] Наконец, для равновесных значений трех вероятностей Pc, Ps и Po получаем: Pseq = 11 + e − βΔGos + e − βΔGcs, Poeq = 11 + e − βΔGco + e − βΔGso, Pceq = 1 − Poeq − Pseq. [S7] Чтобы лучше понять влияние этой конкретной модели канала на количественные прогнозы, мы также исследовали более простая модель, которая не учитывала субпроводимость и включала одно открытое и одно закрытое состояние.Уравнения, управляющие Pc и Po, аналогичны уравнению. S5 и уравнение. S6 . Средний ионный ток через единственный канал определяется выражением j = Poio + Psis, где is и io представляют максимальные токи в субпроводимости и открытой конформации, соответственно; ток в замкнутом состоянии равен нулю. Средний макроскопический ток, протекающий через весь нейрон, представляет собой сумму токов, протекающих по его каналам, то есть I = ∑kjk, [S8], где jk — ток канала k -го.Для совокупности N идентичных каналов ожидаемое количество элементов в открытом состоянии и состоянии субпроводимости и соответствующий полный ток равны 〈ns〉 = N Ps, 〈no〉 = N Po, 〈I〉 = N [isPs + ioPo] , [S9] где ns, o — количество каналов в субпроводимости и открытой конформации, соответственно. Две экспериментальные оценки одноканального тока доступны для каналов C. elegans MeT, смоделированных здесь. Первая оценка получена из стационарного анализа шума in vivo (12), вторая — из одноканальных записей MEC-4-зависимых каналов, экспрессируемых в гетерологичных клетках (14).Мы используем значение одноканальных токов, согласующееся с обоими экспериментальными измерениями: -1,6 ± 0,2 пА. В то время как одноканальная проводимость фиксирована, ожидается, что количество каналов, активируемых во время данного механического воздействия, будет переменным. В частности, вероятность нахождения в открытом состоянии будет варьироваться в зависимости от положения канала относительно точки стимуляции. Экспериментальные данные показывают, что каналы локализуются в дискретных точках, распределенных вдоль нейрита, без явного базального / апикального смещения и что распределение межпунктовых интервалов приблизительно логнормально и со средним межпунктовым расстоянием около 2 мкм (32).Ожидается, что деформации тела червя, возникающие при механическом воздействии, будут сильнее в области, близкой к точке вдавливания. Отсюда следует, что различные каналы и их якоря будут подвергаться различным уровням механической стимуляции, которые отражены в формуле. S4 через зависимость функции χ от недеформированного положения Xa. Следующее приближение [типа среднего поля, распространенного в статистической физике (19)] позволяет нам упростить модель и оценить сумму в уравнении. S8 . Зависимость χ от Ха в уравнении. S4 сокращается до двух возможных классов: набор каналов с уникальным ненулевым значением χ , а остальные из них имеют χ = 0, например, потому что они слишком далеко от точки вдавливания. Количество активных каналов (χ ≠ 0) зависит от следующих факторов. Точечное вдавливание упругой сферической оболочки приводит к профилям деформации с масштабированием растяжения как степенным законом вдавливания; см., например, ссылки.19, 63 для случая без внутреннего давления или с внутренним давлением, и аналогичное поведение имеет место для шара, вдавливающего цилиндр с внутренним давлением. Каналы в пределах типичной шкалы длины деформации (микрометры) обеспечивают верхнюю оценку количества активных каналов, которая достигается в результате быстрых вдавливаний. С другой стороны, мы физически ожидаем, что если окончательная деформация будет производиться медленно, количество активных каналов будет уменьшено. Поэтому ожидается, что количество активных каналов будет увеличиваться по мере изменения вдавливания и уменьшаться в некоторых типичных временных масштабах релаксации, сравнимых с динамикой филамента, т.е.е., чтобы иметь поведение, подобное | x | как определено в предыдущем разделе. Это замечание предполагает, что вместо того, чтобы вводить независимую динамику с набором дополнительных параметров, мы могли бы экономно использовать | x | в качестве заместителя числа активных каналов и введите логарифмический член в разность свободной энергии между закрытыми и открытыми формами каналов: βΔGoc = xh− | x | xs − p log (| x |), [S10] с (положительная) экспонента p оставлена как подгоночный параметр. Логарифмический член в уравнении. S10 вводит зависимость | x | p в отношении Po / Pc, т. Е. Увеличивает истощение каналов в открытом состоянии и оставляет их закрытыми при малых удлинениях (малых | x |). Первый член в правой части уравнения. S10 — это стандартная форма Больцмана, которая способствует линейному открытию канала по мере удлинения нити накала. Две константы xh и xs являются свободными параметрами, которые также поглощают член, делающий логарифм безразмерным. Зависимость формы Больцмана от | x | для описания наблюдаемого симметричного ответа нейрона на приложение и снятие механических нагрузок.Наконец, свободная энергия состояния субпроводимости может априори иметь функциональную зависимость и / или параметры, отличные от уравнения. S10 , но, опять же, чтобы минимизировать свободные параметры, мы делаем предположение, что его свободная энергия является промежуточной между закрытым и открытым состояниями ΔGos = aΔGoc; ΔGsc = (1 − a) ΔGoc, [S11] с единственным параметром 0≤a≤1. Обратите внимание, что подход среднего поля резко снижает сложность проблемы: совокупность многих каналов заменена одним «эффективным» каналом, который реагирует на стимулы, кодируемые удлинением прикрепленной к нему нити эффективным потенциалом. Уравнение S10 , который включает свойства отдельных каналов и всего их ансамбля. В частности, ток, протекающий через нейрон, эквивалентен току, переносимому по единственному эффективному каналу, то есть средний ионный ток (уравнение S8 ) определяется выражением I = PoIo + PsIs, [S12], где Io и Is являются максимальные токи в открытом и субпроводящем состоянии эффективного канала соответственно. Максимальный ток I0 нашего эффективного канала примерно равен произведению максимального тока i0 для одного реального канала, умноженного на количество каналов, которые подвергаются максимальной стимуляции для наших условий подготовки и стимуляции.Сравнивая значения Io, которые мы сообщаем в таблицах S1 и S2, с экспериментальным значением io = -1,6 пА, упомянутым выше для одиночных каналов, мы заключаем, что наш эффективный канал включает в себя проводимость около N≃15-30 реальных каналов. Этот диапазон качественно согласуется с количеством активированных каналов, оцененным в предыдущей работе (12). Обратите внимание, что это число, как ожидается, будет варьироваться в зависимости от условий подготовки и стимуляции, а именно от максимального расширения поля деформации в экспериментальной установке, используемой для стимуляции животного.Связь Is со значениями, измеренными экспериментально (14), менее прямая. Это связано с тем, что Is не относится к состоянию, однозначно идентифицируемому, например, к максимальному значению тока, протекающего через нейрон, в случае Io. В частности, оценка Is чувствительна к промежуточным значениям тока, протекающего через нейрон, который в действительности представляет собой совокупность нескольких каналов, занимающих различные состояния проводимости. В нашей обработке среднего поля совокупность каналов фиксируется только эффективно, и значение Is, таким образом, связано с динамикой вероятностей Pc, s, o. Оцененные выше значения N не влияют ни на одно из последующих прогнозов, которые включают средний ток и, следовательно, значения Io и Is. В частности, значение N = 25 использовалось только для построения доверительных интервалов наших прогнозов через ожидаемую дисперсию тока, оцененную как σI2 = 1N [Is2Ps (1 − Ps) + Io2Po (1 − Po) −2Is IoPsPo. ]. [S13] В заключение отметим, что при выводе свободной энергии мы предполагали зависимость от | x | для обеспечения симметричной реакции на приложение и снятие механических нагрузок.Остается неизвестным, сохраняется ли симметрия на уровне отдельных каналов MeT или является макроскопическим свойством ансамбля каналов, которые украшают нейроны рецептора прикосновения. Для модели, схематически изображенной на рис. 4 основного текста, первая ситуация была бы реализована, если бы точка прикрепления нити к каналу могла скользить по окружности канала. Тогда эта система будет по существу аналогична люку, перекрывающему канал и скользящему вбок при механической стимуляции.И наоборот, если бы точка прикрепления нитей была фиксированной, отдельные каналы MeT имели бы предпочтение в направлении их стимуляции; симметрия реакции ансамбля будет восстановлена как следствие случайного положения каналов и их нитей вдоль нейрита. На уровне среднего тока нейрона несимметричный случай аналогичен симметричному с меньшей плотностью каналов вдоль нейрита. Дополнительные вязкоупругие модели.Чтобы улучшить качество теоретических предсказаний, мы представляем две дополнительные модели вязкоупругого взаимодействия между деформацией тела и активацией канала. Эти модели связаны с быстрыми изменениями внешних нагрузок, которые должны исследовать тонкую структуру вязкоупругой динамики. Вкратце, мы обнаружили, что в то время как уточненные вязкоупругие модели действительно улучшают описание экспериментальных данных, более простая модель Кельвина фиксирует основные закономерности. Член трения, введенный в уравнение. S2 предполагает мгновенный отклик среды. В действительности обычно требуется конечное время, и простейшая модель, отражающая этот эффект, следующая: (v (t)) = — γ∫ − ∞tK (t − u) v (u) du, [S14] где K — это ядро трения, а v (t) — относительная скорость объекта, движущегося в вязкоупругой среде. Ниже мы покажем, что ядро вида K (t) = 1ηe− (t / η), [S15] приводит к стандартной вязкоупругой линейной модели (9, 11) и согласуется с нашими экспериментальными данными. Если память ядра пренебрежимо мала относительно характерного времени изменения v , тогда уравнение трения S14 сводится к уравнению.(s) из x (t). Это выражение для стандартной модели линейного твердого тела (SLS) (также известной как обобщенная модель Максвелла – Вихерта в простейшем варианте с двумя элементами, пружиной параллельно модулю Максвелла, т. Е. Еще одной пружиной, включенной последовательно с приборной панелью. ) (9, 11). Как обсуждалось выше, модель SLS сводится к контрольной точке, параллельной пружине, то есть модулю Кельвина, когда память о фрикционном члене незначительна (9, 11). Интегральное уравнение. S16 решается путем введения вспомогательной переменной m (t) = ∫ − ∞tK (t − u) [x (u) −χ ζ (u)] du, интегрирования по частям и использования экспоненциальной формы Eq. S15 для получения дифференциальных уравнений {dm (t) dt = −1τ + η [m (t) + χζ (t)], x (t) = ττ + η [m (t) + χζ (t)] . [S17] Подтверждено, что свойство адаптации и двухпозиционная симметрия отклика, которые обсуждались в Динамика нити канал-якорь выше для уравнения. S4 для модели SLS Ур. S16 тоже. Вязкоупругие модели, более сложные, чем модуль Кельвина и модель SLS, включают рациональные функции более высокого порядка по переменной Лапласа и обычно исследуют производные более высокого порядка по времени (9, 11).Как обсуждалось, мы также ожидаем, что дифференциальные смещения и функция χ в уравнении. S3 имеют некоторую зависимость от скорости вдавливания. Эти дополнительные условия могут сильно повлиять на прогнозы, например, для протоколов стимуляции, которые включают экстремальные временные колебания. Чтобы оценить эти эффекты и надежность наших прогнозов, мы записали (и сравнили результаты с предыдущими моделями) следующую общую вязкоупругую модель: σ1d2xdt2 + dxdt + 1τx = χ (dζ (t) dt + σ2d2ζ (t) dt2), [ S18], который содержит производные по времени до второго порядка.Параметры τ , σ1 и σ2 в уравнении. S18 — три независимые постоянные времени. Эта структура уравнения. S18 можно получить, моделируя вязкоупругое взаимодействие между якорем и средой с помощью приборной панели последовательно с модулем Кельвина (9, 11) и заменяя уравнение. S3 через xa (t) −S (Xa, t) ∼x (t) — (χ (Xa) ζ (t) + χ1 (Xa) (dζ (t) / (dt)) +…), что учитывает возможные вязкоупругие зависимости от истории внешнего воздействия. Уравнение S18 затем получается с использованием приближения сверхдемпфирования, сохраняя производные по времени до второго порядка и изменяя масштаб константы первой производной. В заключение, мы ожидаем от сравнения между моделями уравнений. S4 , S16 , и S18 , что любые исправления или улучшения модели будут относительно незначительными, по крайней мере, для доступных в настоящее время профилей стимуляции. Таким образом, преждевременно рассматривать эффекты высшего порядка и нелинейные эффекты, что объясняет природу модельного уравнения. S18 и тот факт, что мы использовали уравнение модели SLS. S16 для прогнозов, показанных в основном тексте. Сравнение с экспериментальными данными.Мы оценили способность теоретических моделей восстанавливать динамику отклика тока MeT следующим образом. Прогнозы в основном тексте были получены путем оптимизации параметров по всему ансамблю форм сигналов стимула, применяемых во время данной записи. Затем мы проверили надежность прогнозов, варьируя модель и параметры, например, мы спросили, насколько хорошо параметры модели, полученные из реакции на импульсы вдавливания, могут воспроизводить ответы на сигналы произвольной формы и на синусоидальную стимуляцию.Наиболее строгое сравнение было проведено для двух записей (идентифицированных по их лабораторным индексам 169 и 173), в которых был получен полный набор данных, включая реакцию на серию импульсов вдавливания, синусоидальных стимулов и стимулов с изменением и удержанием. Таким образом, мы сосредотачиваемся на этих двух наборах данных и демонстрируем ниже, что модель достаточно надежна, чтобы параметров, полученных из одной записи, было достаточно, чтобы уловить основные особенности другой записи. Вывод параметров моделей.Для всех вязкоупругих моделей, представленных выше, параметр χ может быть установлен на единицу путем изменения масштаба x и переопределения параметров xh и xs, появляющихся в уравнении. S10 . Что касается скоростей конформационных переходов, скупая форма, соблюдая подробные уравнения баланса ограничений. S 6 и S11 isRsc = rcse (1 + b) (1-a) βΔGoc; Rcs = rcseb (1-a) βΔGoc; Ros = rsoe (1 + d) aβΔGoc; Rso = rsoedaβΔGoc. [S19] Здесь rcs (rso) управляет скоростью переходов между закрытым и субпроводящим состояниями (субпроводимостью и открытым состоянием), а параметры b и d управляют их глобальным сдвигом относительно вариациям разности свободных энергий.Поскольку ожидается, что вероятность открытия каналов будет расти с | x |, параметры b , d ограничены диапазоном −1≤b≤0. Параметры моделей выводятся из сравнения с экспериментальными кривыми с использованием функции оптимизации lsqcurvefit , доступной в MATLAB. Оптимизация находит параметры, которые лучше всего воспроизводят данные, , а именно ., Дают расстояние по методу наименьших квадратов между прогнозируемым и наблюдаемым профилями тока.Эта процедура дала параметрам различных моделей значения, показанные в таблицах S1 и S2 для записей 169 и 173, соответственно. Результаты.Прогнозы для модели SLS Ур. S16 находятся в основном тексте. Здесь мы приводим дополнительные кривые на рис. S2 и S3 для записей 169 и 173 соответственно. Один набор параметров используется для соответствия ансамблю кривых, то есть линейным изменениям, шагам и синусоидам для каждой из двух записей. Оптимальные параметры модели различаются между двумя записями, как и ожидалось, исходя из различий в механических свойствах вскрытых животных (рис.1 С ). Несмотря на это изменение, точная настройка не потребовалась, и значения для двух наборов параметров аналогичны. Принимая во внимание многомерный характер набора параметров, лучшая демонстрация представлена на рис. S3, где мы вычислили отклик записи 173, используя оптимальные параметры для записи 169, и сравнили результат с экспериментальными кривыми для запись 173. Несмотря на то, что некоторое расхождение очевидно, общее согласие очень хорошее и подтверждает согласованность двух наборов параметров. Соответствующее замечание к кривым на рис. S2 и S3 — это насыщение ответа на высоких частотах, то есть тот факт, что ответ не следует за стимуляцией и устанавливается на постоянный уровень. В основном это связано с инерционностью каналов; ожидаемые конформационные переходы не могут следовать за стимуляцией, когда его колебания слишком быстрые. Населения в конформационных состояниях каналов устанавливаются затем примерно до постоянных значений (с шумом). На рис.S4, мы показываем, как параметры модели, полученные из реакции только на импульсы вдавливания, могут воспроизводить ответ на стимулы с нарастанием и удержанием и синусоидальную стимуляцию (для той же записи). Другими словами, мы оптимизируем параметры на подмножестве экспериментальных данных, а затем сравниваем прогнозируемый ток для остальных экспериментальных стимулов. Несмотря на то, что глобальная оптимизация дает лучшее описание, прогнозы явно совместимы с экспериментами. Далее мы сравним качество прогнозов для различных моделей Eqs. S4 , S16 и S18 . Мы обнаружили, что в обеих записях характеристики моделей схожи, а различия можно увидеть только в тонкой структуре кривых. Некоторые репрезентативные графики показаны на рис. S5 для записи 169. Для ясности мы сообщаем только результаты SLS, как модели Кельвина и SLS в уравнениях. S4 и S16 дают практически одинаковые результаты. Это согласуется с тем фактом, что предполагаемое время запоминания η составляет порядка 10-5 с, т.е.е., примерно на 2 порядка быстрее, чем в любой временной шкале экспериментальных стимуляций. Общая модель второго порядка Eq. S18 немного улучшает качество прогнозов. В частности, мы наблюдаем, что реакция на шаги лучше отражает резкие изменения стимуляции и ближе к экспериментальным результатам по сравнению с другими моделями. Однако различия относительно незначительны и не вполне достаточны, чтобы количественно охарактеризовать характер поправок к основным уравнениям модели. S4 и S16 . Для этого потребуется экспериментальная установка следующего поколения, которая в настоящее время находится в стадии разработки, с более расширенным набором данных для однократной записи, более высокими частотами стимуляции и уменьшенным шумом приборов, чтобы точно измерить слабые токи, генерируемые медленными стимуляциями. Наконец, сравним на рис. S6 и S7 результаты для модели Кельвина с двумя или тремя конформационными состояниями. Для обеих записей 169 и 173 прогнозы с тремя состояниями дают немного лучшее соответствие, но основное поведение уже зафиксировано моделью с двумя состояниями (с меньшим количеством параметров).Суть в том, что поведение различных вязкоупругих моделей относительно похоже, и полученные прогнозы для имеющихся профилей стимуляции устойчивы по отношению к деталям моделей. БлагодарностиМы благодарим Валерию Васкес, Александра Ганьона, Фредерика Луазо и Сильвию Фехнер за вклад и Zhiwen Liao за техническую поддержку. Изготовление проводилось на Стэнфордском предприятии по нанотехнологиям, которое поддерживается Национальным научным фондом через Национальную сеть инфраструктуры нанотехнологий (грант ECS-9731293).A.L.E. был поддержан премией Рут Л. Киршштейн (F32NS065718) и B.C.P. была поддержана стипендиями для аспирантов Национального научного фонда. Стэнфордский университет оказал поддержку NIH (грант R01NS07715 для M.B.G. и грант R01EB006745 для M.B.G. и B.L.P.). Сноски
Доступен бесплатно в режиме онлайн через опцию открытого доступа PNAS. Морфомеханика супраструктур человеческого коллагена, выявленная с помощью полностью оптической корреляционной микроспектроскопииПодготовка образцаЭто исследование было проведено в соответствии с принципами Хельсинкской декларации. Здоровые роговицы человека были приобретены в Veneto Eye Bank Foundation (Венеция, Италия) после отбора среди тех, которые не подходят для трансплантации. После сбора образцы хранились в растворе для консервации тканей (CARRY-C, Alchimia srl, Падуя, Италия) не более трех дней с момента доставки, а затем обрабатывались в соответствии с протоколом, обеспечивающим сохранение их механической целостности и морфологии 52 .Сначала образцы фиксировали в течение 24 часов в фосфатно-солевом буфере с 4% параформальдегидом и промывали тем же буфером перед подготовкой к визуализации. Затем роговичную пуговицу отделяли от склеры с помощью Barron Donor Cornea Punche (Katena Products, Inc., Корт Денвилл, Нью-Джерси, США) и вставляли в самодельную камеру, сделанную путем смещения двух стеклянных покровных стекол, запечатанных клеем и заполненных фосфатом. забуференный физиологический раствор для поддержания физиологической осмолярности. Один образец, представленный на дополнительном рисунке 1, был проанализирован перед любым протоколом фиксации. Чтобы точно отобразить одно и то же поле зрения с помощью SHG, Бриллюэна и рамановской микроскопии, с помощью лазерной абляции на эпителии роговицы был выжжен характерный узор из меток, как показано на рис. 5a). Каждая метка была нанесена как фототермическое повреждение при использовании мощности лазера около 30 мВт и при освещении области 10 × 10 мкм 2 . Пространственное ограничение абляции и отсутствие повреждений нижележащей коллагеновой стромы было подтверждено путем получения стопки изображений в самой верхней строме, непосредственно под мембраной Боумена, с помощью ГВГ микроскопии (рис.5б). На рис. 5в показано объединение изображений на рис. 5а, б. Чтобы исследовать неповрежденную ткань роговицы и избежать любого возможного влияния процесса абляции, коррелятивное исследование ГВГ, комбинационного рассеяния света и Бриллюэна проводилось на расстоянии не менее 60 мкм в радиальном направлении и нескольких десятков микрон вдоль оптической оси от каждого реперного пятна. Рис. 5Экспериментальные установки для корреляционной ГВГ, Бриллюэновской и Рамановской микроскопии. a Эпителий роговицы, отображаемый с помощью двухфотонной флуоресценции, отображающий образец лазерной абляции, используемый в качестве реперных маркеров.Масштабные линейки: 60 мкм. b Проекция максимальной интенсивности пакета изображений ГВГ, полученная в строме роговицы под маркерами лазерной абляции, показывающая неповрежденный узор ламелл коллагена. c Объединение изображений, показанных в ( a ) и ( b ), с флуоресценцией, закодированной красным, и SHG серым. d Оптическая схема экспериментальной установки для ГВГ микроскопии. Путь возбуждения лазера показан красным, а пути обнаружения показаны зеленым и синим для флуоресценции и ГВГ соответственно.(Линза L , зеркало M , затвор S , полуволновая пластина λ /2, поляризатор PBS , λ /4 четвертьволновая пластина, гальванометрическое зеркало Gm , сканирующая линза SL , Трубчатая линза TL , дихроичное зеркало D , поляризационный сканер PS , линза объектива OBJ , блокирующий лазерный фильтр B , флуоресцентный фильтр FF , полосовой фильтр BF , фотоумножитель PMT трубка). e Оптическая схема экспериментальной установки, используемой для микроскопии Бриллюэна и комбинационного рассеяния света (BM и RM), состоящая из конфокального микроскопа, высококонтрастного тандемного интерферометра Фабри-Перо и рамановского спектрометра. Лазерный источник LS , эталон с регулируемой температурой TCF , зеркало M , расширитель луча BE , широкополосный поляризационный светоделитель BS , четвертьволновая пластина λ /4, коаксиальный светодиодный осветитель LI , Объектив OBJ , 3-осевой пьезоэлектрический преобразователь SH , настраиваемый ультракороткий короткочастотный фильтр TEF , спектрометр Бриллюэна TFP-2-HC Tandem Fabry Perot-2-High Contrast, SPAD однофотонная лавина фотодиод, LPF фильтр длинного прохода, RM Рамановский спектрометр) Установка для визуализации SHGИзготовленный на заказ нелинейный микроскоп с лазерным сканированием, установленный на вертикально расположенном сотовом макете из нержавеющей стали, использовался для визуализации SHG (Инжир.5г). В качестве источника лазера использовался Ti: Sapphire-лазер с синхронизацией мод (Mira 900 F, Coherent Inc., Санта-Клара, Калифорния, США), накачиваемый лазерной системой Nd: YVO 4 с удвоенной частотой, излучающей на длине волны 532 нм (Verdi V10 , Coherent Inc., Санта-Клара, Калифорния, США). Для визуализации коллагена с помощью SHG длина волны возбуждения была настроена на 840 нм. После коллимирующего телескопа (L1, L2) и электронного затвора (S) была реализована система, состоящая из вращающейся полуволновой пластины ( λ /2) и поляризатора (PBS) для точной регулировки мощности лазера, тогда как четвертьволновая пластинка ( λ /4) использовалась для управления состоянием поляризации в задней фокальной плоскости линзы объектива и для компенсации аберраций, вносимых оптическими компонентами.В этом исследовании использовалась либо линейная, либо круговая поляризация, чтобы соответственно получить отклик ГВГ, который не зависит от поляризации или зависит от поляризации. Лазерный луч сканировался в растре на образце с помощью двух ортогональных гальванометрических зеркал (Gmx, Gmy, VM500, GSI Lumonics, Карлсруэ, Германия), оптически ретранслированных двумя линзами (L3, L4, f = 60 мм) в конфигурации 4 ф. После прохождения через сканирующую головку лазерный луч был расширен до размера около 1 см с помощью телескопа, сделанного путем сканирования (SL) и линзы трубки (TL), перед фокусировкой линзой объектива Plan-Apochromat × 40. (OBJ1, NA 1.4, WD 0,13 мм, Carl Zeiss Microscopy, Йена, Германия). Для чувствительного к поляризации сбора поляризационный сканер, реализованный с полуволновой пластиной, вставленной в моторизованную вращающуюся опору, был помещен непосредственно перед диафрагмой объектива, чтобы возбуждать образец с линейной поляризацией контролируемой ориентации. Флуоресценция, испускаемая образцом, собиралась той же линзой объектива, которая использовалась для возбуждения, отражалась дихроичным зеркалом (D1, 685DCXRU Chroma Technology Corporation, Rockingham, VT, US) и направлялась в фотоэлектронный умножитель (PMT1, H7422 Hamamatsu, Hamamatsu Город, Япония).ГВГ прямого излучения собирали с помощью иммерсионного объектива Fluor × 40 (OBJ2, NA 0,8, WD 2 мм, Nikon Corporation, Токио, Япония), отраженного дихроичным зеркалом (D2, 685DCXRU Chroma Technology Corporation, Rockingham, VT, США) и регистрируется фотоэлектронным умножителем (PMT2, H7422 Hamamatsu, Hamamatsu City, Japan). Узкий полосовой фильтр с центром на 420 ± 10 нм (BF, HQ420BP Chroma Technology Corporation, Rockingham, VT, US) был помещен в тракт обнаружения для избирательного обнаружения света второй гармоники.Два короткопроходных фильтра были вставлены в тракты обнаружения флуоресценции и ГВГ (B1, B2, E700SP-2P Chroma Technology Corporation, Rockingham, VT, US), чтобы отклонить любой рассеянный лазерный свет. Получение и анализ изображений SHGИзображения и стопки SHG были получены из центральной части образцов роговицы с использованием геометрии оптического сечения спереди (оптическая ось, ортогональная поверхности ткани) и схемы прямого обнаружения. Параметры изображения: поле зрения 200 × 200 мкм 2 , разрешение 1024 × 1024 пикселей 2 , время задержки пикселя 20 мкс, длина волны 840 нм и средняя мощность лазера около 8 мВт.Пространственное разрешение составляло около 300 нм в радиальном направлении и 1000 нм по оптической оси. Чтобы сопоставить изображения ГВГ с изображениями, полученными в микроскопе Бриллюэна-Рамана, мы применили пространственное объединение данных ГВГ, чтобы реализовать эффективное согласование разрешения, которое можно получить с помощью двух других методов. Средний наклон шовных пластинок, которые видны в стопках ГВГ, был определен количественно с помощью основанного на автокорреляции метода 35 . Поляризация лазера в BFP в большинстве случаев была круговой и линейной только для измерений P-SHG, где его ориентация изменялась с шагом 20 ° путем вращения полуволновой пластинки (см.рис.{2} \ right), $$ , где d 22 = χ yyy , d 15 = χ xxz , d 31 = χ zxx , d 33 = χ zzz , — элементы тензора восприимчивости второго порядка, α — угол между осью фибриллы и ориентацией поляризации, A — нормировочный коэффициент. Поскольку χ yyy отклоняется от нуля и увеличивается по абсолютной величине по мере того, как тригональная симметрия возникает над цилиндрической (см. Следующий абзац), мы определили параметр симметрии, который отражает эту тенденцию.Для увеличения чувствительности этого параметра к супрамолекулярной симметрии коллагена мы использовали соотношение между модулем χ yyy и χ zxx , т.е. S = | d 22 | / d 31 = | χ ггг | / χ zxx. Мы реконструировали карты S с пространственным разрешением, анализируя каждый пиксель. Рис.6Стек изображений P-SHG. Пример набора изображений P-SHG, взятых из образца роговицы человека, полученного с использованием сагиттальной геометрии оптического сечения.Направление поляризации изменяется с шагом 20 °, что схематично показано вставками с красными стрелками в правом верхнем углу изображений. Ориентация поляризации относительно горизонтальной оси изображения следующая: a 0 °, b 20 °, c 40 °, d 60 °, e 80 °, f 100 °, g 120 °, h 140 °, i 160 °, j 180 °. Поле зрения: 200 × 200 мкм 2 . Разрешение: 1024 × 1024 пикселей 2 Математическая модель P-SHGВ нелинейной оптике оптические процессы второго порядка, такие как SHG, зависят от поляризации второго порядка, которая определяется уравнением: $ $ P_i \ left ({2 \ omega} \ right) = 2 \ mathop {\ sum} \ limits_ {jk} \ mathop {\ sum} \ limits_ {nm} \ chi _ {ijk} \ left ({\ omega _n + \ omega _m, \ omega _n, \ omega _m} \ right) E_j (\ omega _n) E_k (\ omega _m), $$ (1) Где ω n и ω m — две различные частоты падающего поля, χ ijk — элементы тензора восприимчивости второго порядка χ ( i, j, k ), соответствующие к направлениям главных осей, E j ( ω n ) и E k ( ω n амплитуд) являются компоненты электрического поля на частоте ω n и ω m соответственно. Для SHG ω n = ω m = ω и ω n + ω m = 2ω, так что уравнение для поляризации имеет вид: $$ P_i \ left ({2 \ omega } \ right) = 2 \ mathop {\ sum} \ limits_ {jk} \ chi _ {ijk} \ left ({2 \ omega; \, \ omega, \ omega} \ right) E_j (\ omega) E_k. $ $ (2) χ — это матрица ранга 3 из 27 элементов, которая может быть упрощена до матрицы из 18 ненулевых элементов из-за симметрии в последних двух индексах (поскольку ω n = ω m = ω в SHG) 53 $$ \ left ({\ begin {array} {* {20} {c}} {P_x} \\ {P_y} \\ {P_z} \ end {array}} \ right) = 2 \ left ({\ begin {array} {* {20} {c}} {\ chi _ {xxx}} & {\ chi _ {xyy}} & {\ chi _ {xzz}} & {\ chi _ {xyz }} & {\ chi _ {xxz}} & {\ chi _ {xxy}} \\ {\ chi _ {yxx}} & {\ chi _ {yyy}} & {\ chi _ {yzz}} & { \ chi _ {yyz}} & {\ chi _ {yxz}} & {\ chi _ {yxy}} \\ {\ chi _ {zxx}} & {\ chi _ {zyy}} & {\ chi _ { zzz}} & {\ chi _ {zyz}} & {\ chi _ {zxz}} & {\ chi _ {zxy}} \ end {array}} \ right) \ left ({\ begin {array} {* {20} {c}} {E_xE_x} \\ {E_yE_y} \\ {E_zE_z} \\ {2E_yE_z} \\ {2E_xE_z} \\ {2E_xE_y} \ end {array}} \ right).$ (3) В предыдущих исследованиях 54,55 , сфокусированных на характеристике коллагеновых фибрилл в образцах роговицы, данные P-SHG были смоделированы с упрощенной формулой х , полученной из предположения о симметрии Клейнмана для коллагеновых фибрилл. Из этого условия следует свободная коммутируемость всех трех индексов i, j, k . Более того, предположение о цилиндрической симметрии в пространственном расположении гармонофор сокращает количество ненулевых членов 56 .При этих предположениях χ принимает форму: $$ \ left ({\ begin {array} {* {20} {c}} 0 & 0 & 0 & 0 & {\ chi _ {xxz}} & 0 \\ 0 & 0 & 0 & {\ chi _ {xxz}} & 0 & 0 \\ {\ chi _ {xxz}} & {\ chi _ {xxz}} & {\ chi _ {zzz}} & 0 & 0 & 0 \ end {array}} \ right). $$ (4) Хотя симметрия Клейнмана часто предполагается для моделирования P-SHG-ответа коллагена, в нескольких приложениях было продемонстрировано, что ее достоверность не соответствует действительности 57 .Причина этой неудачи в том, что в большинстве практических контекстов симметрия Клейнмана выполняется только частично. Это происходит, когда электронные резонансные частоты гармонофоров примерно на порядок меньше, чем частота возбуждения. Второе предположение также наиболее часто используется в экспериментах с P-SHG и основывается на симметрии пространственного распределения гармонофоров, которое предполагается цилиндрическим. Условие цилиндрической симметрии выполняется, когда фибриллы коллагена расположены в шахматном порядке бок о бок и параллельны друг другу 58 .И наоборот, когда эта идеальная фибриллярная геометрия не соблюдается, предположение о цилиндрической симметрии немедленно не выполняется. Если фибриллы коллагена собираются в более общем геликоидальном распределении, тригональная симметрия (3 мкм) является более подходящей моделью для описания их ГВГ. Согласно гипотезе тригональной симметрии χ принимает новую форму: $$ \ left ({\ begin {array} {* {20} {c}} 0 & 0 & 0 & 0 & {\ chi _ { xxz}} & {- \ chi _ {yyy}} \\ {- \ chi _ {yyy}} & {\ chi _ {yyy}} & 0 & {\ chi _ {xxz}} & 0 & 0 \\ {\ chi _ {zxx}} & {\ chi _ {zxx}} & {\ chi _ {zzz}} & 0 & 0 & 0 \ end {array}} \ right).$ (5) Выражение [5] отличается от [4] элементом χ yyy , который не равен нулю, и неравенством: χ xxz ≠ χ zxx 929 . Элемент χ yyy принимает ненулевое значение, которое увеличивается в абсолютном выражении по мере того, как тригональная симметрия преобладает над цилиндрической. Нарушение симметрии Клейнмана вместо этого означает, что χ xxz ≠ χ zxx . Предполагая, что движущее поле распространяется вдоль x , коллагеновая фибрилла ориентирована вдоль z , а электрическое поле поляризовано вдоль направления, которое образует угол α по отношению к оси фибриллы, вектор электрического поля имеет вид: $ $ E_z \ left (\ omega \ right) = E \ left (\ omega \ right) \ cos \ left (\ alpha \ right). $$ (6) $$ E_y \ left (\ omega \ right) = E \ left (\ omega \ right) \ sin \ left (\ alpha \ right). 2 .2} \ right \}. \ End {array} $$ (15) Подгоняя экспериментальные результаты к уравнению [15], мы можем исследовать различные свойства коллагена роговицы, то есть, достаточно ли резонансная частота гармонофоров выше частоты возбуждения, чтобы соответствовать условию Клейнмана и, что более важно, супрамолекулярная сборка коллагеновых фибрилл соответствует геликоидальному или ступенчатому расположению бок о бок. Учитывая, что элемент χ yyy принимает значение, отличное от нуля, поскольку тригональная симметрия преобладает над цилиндрической симметрией, наше определение S (S = | d 22 | / d 31 = | χ yyy | / χ zxx , подробности см. В предыдущем абзаце) подчеркивает нарушение цилиндрической симметрии и служит удобным показателем для измерения степени скручивания коллагеновых пластинок.Этот параметр полезен для характеристики супрамолекулярной симметрии коллагена роговицы и, в частности, для различения шовных пластинок, то есть класса ламелл коллагена, которые локализуются в передней части стромы роговицы в нормальной ткани человека, проходят в случайных направлениях и часто разветвляются и переплетаются неравномерно 33 . Мультимодальная установка для построения изображений Бриллюэна-РаманаМы использовали изготовленную на заказ микроспектроскопическую установку, способную одновременно выполнять визуализацию Бриллюэна и Рамана.На рисунке 5e схематически показана экспериментальная установка: источником света является одномодовый твердотельный лазер (Spectra Physics Excelsior, Spectra Physics K.K., Санта-Клара, Калифорния, США), излучающий одну продольную моду на длине волны 532 нм. Свет направлялся в конфокальный микроскоп (CM-JRS Scientific Instruments) и фокусировался на образец линзой объектива M-Plan Apo × 20 (Mitutoyo, Kawasaki, Япония) с очень большим рабочим расстоянием (WD = 20 мм) и числовая апертура 0,42, что дает пространственное разрешение на образце ~ 2 × 2 × 10 мкм 3 . Линза объектива использовалась как для фокусировки, так и для сбора обратно рассеянного света, который отделялся в соответствии с его частотой настраиваемым ультракоротким короткопроходным фильтром (TEF, SP01-561RU, Semrock Inc., Рочестер, Нью-Йорк, США). ). Антистоксова квазиупруго рассеянная составляющая передавалась на интерферометр Фабри – Перо TFP-2 HC (JRS Scientific Instruments, Table Stable Ltd., Mettmenstetten, Швейцария), в то время как стоксово глубоко неупруго рассеянный свет отражался в сторону трехаксиального рамановского спектрометра iHR320. (RM-Horiba Ltd., Киото, Япония). TFP-2 HC — это высококонтрастный вариант оригинального тандемного многопроходного интерферометра типа Sandercock, обеспечивающий беспрецедентную контрастность более 10 15 с разрешением по частоте 100 МГц. Для построения 2D-изображений спектры комбинационного рассеяния света и Бриллюэна были получены из каждой точки путем пошагового перемещения образца с использованием трехосевого пьезоэлектрического преобразователя (PI 611-3 S Nanocube XYZ, Physik Instrumente (PI) GmbH & Co. KG, Карлсруэ , Германия) с разрешением 0.01 мкм и диапазон перемещения 100 мкм на ось. Для измерений Бриллюэна-Рамана время сбора данных составляло 65 с на точку, а мощность лазера на образце составляла около 10 мВт. Сбор и анализ Бриллюэна-РаманаДля выполнения последовательностей одновременных измерений Рамана / Бриллюэна, синхронизированных с позиционированием образца, была разработана специальная процедура с использованием программного обеспечения LabSpec 5 (Horiba Ltd., Киото, Япония) для получения спектров комбинационного рассеяния и JRS GHOST 7 (JRS Scientific Instruments, Table Stable Ltd., Метменштеттен, Швейцария) для спектров Бриллюэна. Спектроскопия Бриллюэна изучает свет, рассеянный акустическими фононами, термически активированными в материале. По сути, спектры Бриллюэна состоят из пиков, симметрично смещенных по частоте относительно падающего света на величину, ω b , которая относится к M ‘, то есть действительной части продольного модуля упругости, посредством уравнения ω b = q (M ′ / ρ ) 0.2}}. $$ (16) где 2Γ b — ширина пика. Рамановская спектроскопия исследует свет, неупруго рассеянный меж- и внутримолекулярными колебательными модами химических веществ, присутствующих в образце. Благодаря своей высокой молекулярной специфичности, рамановская спектроскопия подходит для анализа химического состава материалов. Пиковые интенсивности пропорциональны концентрации молекулярных частиц, умноженной на их оптическую активность.Следовательно, зондирование модуляции пиковых интенсивностей в различных областях образца дает изображения с контрастом, связанным с молекулярным составом. Однако спектры комбинационного рассеяния не имеют внутреннего спектроскопического маркера для их нормализации. Для устранения возможных паразитных эффектов, связанных с (i) флуктуациями интенсивности лазера, (ii) небольшими различиями в оптическом поглощении образца и (iii) небольшими изменениями в объеме рассеяния, обычно используется пик нормализации. решение.Этот подход позволяет исследовать относительные изменения концентраций одного и того же химического вещества в разных точках образца или проследить относительные изменения концентрации между различными веществами. В нашем случае мы выбрали сигнал амида I в качестве пика нормализации, который стал золотым стандартом как для исследований IR 59 , так и для исследований комбинационного рассеяния 7 . Анализ данных комбинационного рассеяния проводился с использованием специальных кодов Fortran и Matlab. Чтобы точно оценить площадь анализируемых пиков, из каждого сбора данных вычитался фон, снабженный сплайном, учитывающим темные подсчеты и слабую люминесценцию. ТЕМ-визуализацияОбразцы дополнительно получали с помощью просвечивающего электронного микроскопа CM12 (Philips, Амстердам, Нидерланды), работающего при 80 кВ и оснащенного камерой MegaViewG2 (Olympus Corporation, Токио, Япония). Для ПЭМ-визуализации образцы роговицы были разделены на 1 мм 2 фрагментов площади поверхности, которые дважды промывали фосфатно-солевым буфером (0,1 М, pH 7,2), а затем фиксировали свежим глутаральдегидом (2,5%) в том же буфере при 4 ° C в течение 12 ч. Затем все образцы последовательно промывали трижды (15 мин) фосфатно-солевым буфером с последующей фиксацией тетроксидом осмия (1.0%) в том же буфере в течение 1 ч, дважды промывали тем же буфером (по 15 мин), обезвоживали 30, 40 и 50% этанолом в течение 10 мин, затем 70% этанолом в течение 20 мин, затем 80, 95% и чистый этанол в течение 10 минут и с чистым оксидом пропилена в течение 10 минут и, наконец, пропитан смолой Spurr 60 . Ультратонкие срезы инфильтрированных образцов были собраны и нанесены на покрытые углеродом медные сетки с размером ячейки 200, окрашенные уранилацетатом в метаноле (50%) в течение 5 минут и цитратом свинца в течение 8 минут 61 .Цитрат свинца получали в соответствии с предписаниями Venable and Goggeshall 62 . Все процедуры отмывки проводили водой, не содержащей CO 2 , при барботировании азота в течение 30 мин. Сводка отчетовДополнительная информация о дизайне экспериментов доступна в Сводке отчетов по исследованиям природы, связанной с этой статьей. Живем ли мы в симуляции? Шансы примерно 50–50Нечасто, что комик вызывает у астрофизика мурашки по коже, обсуждая законы физики.Но комик Чак Найс сумел это сделать в недавнем выпуске подкаста StarTalk . Ведущий шоу Нил де Грасс Тайсон только что объяснил аргумент о симуляции — идею о том, что мы можем быть виртуальными существами, живущими в компьютерной симуляции. Если это так, симуляция, скорее всего, будет создавать восприятие реальности по запросу, а не моделировать всю реальность все время — во многом как в видеоигре, оптимизированной для визуализации только тех частей сцены, которые видны игроку. «Может быть, поэтому мы не можем путешествовать быстрее скорости света, потому что, если бы мы могли, мы бы смогли попасть в другую галактику», — сказала Найс, соведущая шоу, побудив Тайсона радостно прервать его.«Прежде, чем они смогут его запрограммировать», — сказал астрофизик, обрадовавшись этой мысли. «Итак, программист поставил этот предел». Такие разговоры могут показаться легкомысленными. Но с тех пор, как в 2003 году Ник Бостром из Оксфордского университета написал основополагающую статью об аргументе моделирования, философы, физики, технологи и, да, комики боролись с идеей, что наша реальность является симулякром. Некоторые пытались определить способы, с помощью которых мы можем различить, являемся ли мы симулированными существами.Другие пытались вычислить вероятность того, что мы виртуальные сущности. Новый анализ показывает, что шансы на то, что мы живем в базовой реальности, то есть в существовании, которое не моделируется, в значительной степени равны. Но исследование также демонстрирует, что если бы люди когда-либо развили способность имитировать сознательные существа, шансы в подавляющем большинстве увеличились бы в пользу нас, являющихся виртуальными обитателями чужого компьютера. (Предостережение к такому выводу состоит в том, что нет единого мнения о том, что означает термин «сознание», не говоря уже о том, как его можно моделировать.) В 2003 году Бостром вообразил технологически развитую цивилизацию, которая обладает огромной вычислительной мощностью и нуждается в небольшой части этой мощности для моделирования новых реальностей с сознательными существами в них. Учитывая этот сценарий, его аргумент о моделировании показал, что по крайней мере одно утверждение в следующей трилемме должно быть верным: во-первых, люди почти всегда вымирают, не дойдя до стадии моделирования. Во-вторых, даже если люди дойдут до этой стадии, они вряд ли будут заинтересованы в моделировании своего собственного прошлого.И в-третьих, вероятность того, что мы живем в симуляции, близка к единице. До Бострома фильм Матрица уже внес свою лепту в популяризацию понятия симулированной реальности. И эта идея имеет глубокие корни в западных и восточных философских традициях, от аллегории Платона о пещере до мечты Чжуан Чжоу о бабочке. Совсем недавно Илон Маск придал дополнительный импульс идее о том, что наша реальность — это симуляция: «Вероятность того, что мы находимся в базовой реальности, составляет один к миллиарду», — сказал он на конференции 2016 года. «Маск прав, если вы предполагаете, что [предположения] первая и вторая трилеммы ложны», — говорит астроном Дэвид Киппинг из Колумбийского университета. «Как вы можете это предположить?» Чтобы лучше понять аргумент Бострома о моделировании, Киппинг решил прибегнуть к байесовским рассуждениям. В этом типе анализа используется теорема Байеса, названная в честь Томаса Байеса, английского статистика и министра XVIII века. Байесовский анализ позволяет вычислить шансы того, что что-то произойдет (так называемая «апостериорная» вероятность), сначала сделав предположения об анализируемом объекте (присвоив ему «априорную» вероятность). Киппинг начал с превращения трилеммы в дилемму. Он объединил предложения один и два в одно утверждение, потому что в обоих случаях конечным результатом является отсутствие моделирования. Таким образом, дилемма противопоставляет физическую гипотезу (нет моделирования) гипотезе моделирования (существует базовая реальность — и есть моделирования). «Вы просто присваиваете каждой из этих моделей априорную вероятность», — говорит Киппинг. «Мы просто принимаем принцип безразличия, который является допущением по умолчанию, когда у вас нет никаких данных или склонностей в любом случае.” Таким образом, каждая гипотеза получает априорную вероятность равную половине, , как если бы кто-то подбрасывал монету, чтобы принять решение о ставке. Следующий этап анализа требовал размышлений о «родственных» реальностях — о тех, которые могут порождать другие реальности, — и о «нерожавших» реальностях — о тех, которые не могут моделировать дочерние реальности. Если бы физическая гипотеза была верна, то вероятность того, что мы живем в нерожавшей Вселенной, было бы легко вычислить: она составила бы 100 процентов.Затем Киппинг показал, что даже в гипотезе симуляции большинство симулируемых реальностей будут нерожавшими. Это связано с тем, что по мере того, как симуляции порождают больше симуляций, вычислительные ресурсы, доступные каждому последующему поколению, сокращаются до такой степени, что подавляющее большинство реальностей не будет иметь вычислительной мощности, необходимой для имитации дочерних реальностей, способных вместить сознательные существа. Подсоедините все это к формуле Байеса, и вы получите ответ: апостериорная вероятность того, что мы живем в базовой реальности, почти такая же, как апостериорная вероятность того, что мы являемся симуляцией — с вероятностью, склоняющейся в пользу базовой реальности всего лишь за счет немного. Эти вероятности резко изменились бы, если бы люди создали симуляцию с сознательными существами внутри, потому что такое событие изменило бы шансы, которые мы ранее приписывали физической гипотезе. «Вы можете сразу исключить эту [гипотезу]. Тогда остается только гипотеза моделирования », — говорит Киппинг. «В тот день, когда мы изобретаем эту технологию, шансы на то, что мы настоящие, чуть выше 50–50, почти наверняка не реальны, согласно этим расчетам.В тот день это было бы очень странным празднованием нашего гения ». Результат анализа Киппинга состоит в том, что, учитывая текущие данные, Маск ошибается в отношении вероятности один к миллиарду, которую он приписывает нам, живущим в базовой реальности. Бостром согласен с результатом — но с некоторыми оговорками. «Это не противоречит аргументу о моделировании, который только утверждает что-то о дизъюнкции», — утверждает он. Но Бостром не согласен с выбором Киппинга приписать равные априорные вероятности физической гипотезе и гипотезе моделирования в начале анализа.«Применение принципа безразличия здесь довольно шатко, — говорит он. «С равным успехом можно было бы применить его к трем моим первоначальным альтернативам, что тогда дало бы им по одной трети шанса каждой. Или можно каким-то другим способом разделить пространство возможностей и получить любой желаемый результат ». Такие придирки действительны, потому что нет никаких доказательств, подтверждающих одно утверждение над другими. Эта ситуация изменится, если мы найдем доказательства симуляции. Так можно ли обнаружить сбой в Матрице? Хоуман Овади, специалист по вычислительной математике Калифорнийского технологического института, задумался над этим вопросом.«Если симуляция обладает бесконечной вычислительной мощностью, вы ни за что не увидите, что живете в виртуальной реальности, потому что она может вычислить все, что вы хотите, с желаемой степенью реализма», — говорит он. «Если эта вещь может быть обнаружена, вы должны исходить из того принципа, что [у нее] ограниченные вычислительные ресурсы». Подумайте еще раз о видеоиграх, многие из которых полагаются на умное программирование, чтобы минимизировать вычисления, необходимые для создания виртуального мира. Для Оухади наиболее многообещающим способом поиска потенциальных парадоксов, порождаемых такими сокращениями, являются эксперименты по квантовой физике.Квантовые системы могут существовать в суперпозиции состояний, и эта суперпозиция описывается математической абстракцией, называемой волновой функцией. В стандартной квантовой механике акт наблюдения заставляет эту волновую функцию случайным образом коллапсировать до одного из многих возможных состояний. Физики расходятся во мнениях относительно того, является ли процесс коллапса чем-то реальным или просто отражает изменение наших знаний о системе. «Если это просто симуляция, коллапса не будет», — говорит Оухади. «Все решено, когда смотришь на это.Остальное — просто симуляция, как в этих видеоиграх ». С этой целью Оухади и его коллеги работали над пятью концептуальными вариациями эксперимента с двумя щелями, каждая из которых предназначена для сбивания с толку моделирования. Но он признает, что на данном этапе невозможно узнать, могут ли такие эксперименты работать. «Эти пять экспериментов — всего лишь предположения», — говорит Оухади. Зохре Давуди, физик из Мэрилендского университета в Колледж-Парке, также высказал идею о том, что моделирование с ограниченными вычислительными ресурсами может проявить себя.Ее работа сосредоточена на сильных взаимодействиях или сильном ядерном взаимодействии — одной из четырех фундаментальных сил природы. Уравнения, описывающие сильные взаимодействия, которые удерживают кварки, образуя протоны и нейтроны, настолько сложны, что их невозможно решить аналитически. Чтобы понять сильные взаимодействия, физики вынуждены проводить численное моделирование. И в отличие от любых предполагаемых суперцивилизаций, обладающих безграничной вычислительной мощностью, они должны полагаться на ярлыки, чтобы сделать эти симуляции вычислительно жизнеспособными — обычно рассматривая пространство-время как дискретное, а не непрерывное.Самый продвинутый результат, которого исследователям удалось добиться на основе этого подхода, — это моделирование одного ядра гелия, состоящего из двух протонов и двух нейтронов. «Естественно, вы начинаете спрашивать, если бы вы смоделировали атомное ядро сегодня, может быть, через 10 лет, мы могли бы создать более крупное ядро; возможно, через 20 или 30 лет мы сможем создать молекулу », — говорит Давуди. «Кто знает, может быть, через 50 лет вы сможете сделать что-то размером с несколько дюймов материи. Может быть, лет через 100 мы сможем создать [человеческий] мозг.” Давуди считает, что классические компьютеры скоро наткнутся на стену. «Возможно, в следующие 10-20 лет мы действительно увидим пределы наших классических моделей физических систем», — говорит она. Таким образом, она обращает внимание на квантовые вычисления, которые полагаются на суперпозиции и другие квантовые эффекты, чтобы сделать решаемыми определенные вычислительные проблемы, которые были бы невозможны с помощью классических подходов. «Если квантовые вычисления действительно материализуются в том смысле, что это крупномасштабный и надежный вариант вычислений для нас, то мы вступаем в совершенно другую эру моделирования», — говорит Давуди.«Я начинаю думать о том, как выполнить мое моделирование физики сильного взаимодействия и атомных ядер, если бы у меня был жизнеспособный квантовый компьютер». Все эти факторы заставили Давуди задуматься о гипотезе моделирования. Если наша реальность является симуляцией, то симулятор, вероятно, также дискретизирует пространство-время, чтобы сэкономить на вычислительных ресурсах (при условии, конечно, что он использует те же механизмы, что и наши физики для этой симуляции). Сигнатуры такого дискретного пространства-времени потенциально можно было бы увидеть в направлениях, откуда приходят космические лучи высоких энергий: они имели бы предпочтительное направление в небе из-за нарушения так называемой вращательной симметрии. Телескопы«еще не наблюдали никаких отклонений от этой инвариантности вращения», — говорит Давуди. И даже если бы такой эффект можно было увидеть, он не стал бы однозначным доказательством того, что мы живем в симуляции. Сама базовая реальность могла иметь аналогичные свойства. Киппинг, несмотря на собственное исследование, обеспокоен тем, что дальнейшая работа над гипотезой моделирования идет по тонкому льду. «Возможно, невозможно проверить, живем ли мы в симуляции или нет», — говорит он. «Если это невозможно опровергнуть, то как вы можете утверждать, что это настоящая наука?» Для него есть более очевидный ответ: бритва Оккама, которая говорит, что в отсутствие других доказательств наиболее простое объяснение с большей вероятностью будет правильным.Гипотеза моделирования является сложной, предполагая, что реальности вложены в реальности, а также моделируемые сущности, которые никогда не могут сказать, что они находятся внутри моделирования. «Поскольку это слишком сложная, тщательно продуманная модель, во-первых, с точки зрения бритвы Оккама, она действительно не заслуживает одобрения по сравнению с простым естественным объяснением», — говорит Киппинг. Может быть, мы все-таки живем в базовой реальности — Матрица, Маск и странная квантовая физика. Распределение времени пребывания молекулярного моторного миозина VЦитирование: Bierbaum V, Lipowsky R (2013) Распределение времени пребывания молекулярного моторного миозина V.PLoS ONE 8 (2): e55366. https://doi.org/10.1371/journal.pone.0055366 Редактор: Фредди-младший Салсбери, Университет Уэйк Форест, Соединенные Штаты Америки Поступила: 25.09.2012; Одобрена: 21 декабря 2012 г .; Опубликовано: 13 февраля 2013 г. Авторские права: © 2013 Bierbaum, Lipowsky. Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника. Финансирование: У авторов нет поддержки или финансирования, чтобы сообщить. Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов. ВведениеМолекулярный моторный миозин V представляет собой димерный белок с двумя идентичными моторными доменами или «головками», каждый из которых имеет нуклеотид-связывающий карман для гидролиза АТФ. Мотор преобразует свободную энергию, высвобождаемую при гидролизе АТФ, в дискретные механические ступени вдоль актиновых филаментов [1], [2].Свойства этих стадий характеризовались изменением концентрации АТФ и внешней нагрузки в различных экспериментах с одной молекулой и хемокинетике [2] — [10], включая живые клетки [11]. Детали механических шагов двигателя были исследованы с использованием сложных методов работы с одной молекулой [12] — [15]. Более того, движение двигателя было непосредственно визуализировано с помощью АСМ изображения [16]. За один шаг вперед двигатель отсоединяет заднюю головку от нити, перемещает эту головку вперед на 72 нм и повторно прикрепляет ее к нити перед другой головкой.Поскольку последняя головка остается в фиксированном положении нити накала, во время такого шага центр масс двигателя смещается на 36 нм. Это направленное движение требует координации гидролиза АТФ двумя головками двигателя. Принято считать, что эта координация включает следующие двигательные состояния и переходы. Большую часть своего времени моторная молекула находится в фиксированном положении филамента с АДФ, связанным с обеими головками. Последовательность, которая приводит к шагу вперед, начинается с высвобождения АДФ из задней головки двигателя с последующим связыванием АТФ с этой головкой, в то время как ведущая головка двигателя остается в состоянии АДФ.Таким образом, разные скорости выпуска ADP для ведомой и ведущей головок, которые мы будем описывать как стробирующие, важны для координации этих двух головок. Однако до сих пор не было возможности напрямую измерить эти две скорости для двуглавого миозина V. Эксперименты с одноголовым миозином V показывают, что силы сопротивления и поддержки нагрузки приводят к скоростям, которые могут различаться до 100 раз [ 8], [9], [17], [18]. В двуглавой молекуле внутримолекулярная деформация приводит к возникновению противоположных сил на двух головках двигателя.Следовательно, эксперименты с одноголовым миозином V предполагают, что разные скорости высвобождения будут зависеть также от силы. В настоящем исследовании мы будем называть разницу в скорости высвобождения АДФ стробированием. Обратите внимание, что последний термин используется разными авторами в несколько разном значении. Эта статья тесно связана с нашей предыдущей работой, в которой мы обсуждали сетевое описание миозина V, которое фиксирует шаговые свойства двигателя как функцию внешних управляющих параметров, таких как концентрация нуклеотидов и сила внешней нагрузки [19].Скорость шага миозина V зависит от концентрации АТФ и уменьшается с уменьшением [АТФ]. Для силы нагрузки, противоположной направлению шага двигателя, нагрузка снижает скорость двигателя до тех пор, пока эта скорость не исчезнет при силе срыва pN [3], [4], [6], [7]. При сопротивлении нагрузкам, превышающим усилие срыва, двигатель проявляет храповое поведение, т.е. е., он отступает, не подвергаясь сильному влиянию АТФ. Для вспомогательных нагрузок скорость шага двигателя не зависит от силы нагрузки.В нашем предыдущем исследовании [19] движение двигателя описывалось хемомеханической сетью, которая включает в себя как химические реакции, обеспечиваемые связыванием и высвобождением нуклеотидов, так и два механических ступенчатых перехода, оба из которых имеют одинаковый размер шага (нм ). Шаговые свойства мотора как для вспомогательных, так и для вспомогательных сил, были описаны тремя различными мотоциклетными циклами: хемомеханическим, ферментативным и механическим шаговым циклом. Более того, стробирующий эффект был включен за счет различной скорости высвобождения АДФ в ведущей и задней головках молекулы. В этой статье мы определим соотношение двух скоростей высвобождения АДФ путем анализа распределения времени задержки, измеренного для двуглавого двигателя. Мы выводим это соотношение, называемое параметром стробирования, путем сравнения трех циклов, обсуждаемых в [19], с экспериментальными распределениями времени пребывания, которые доступны для миозина V [4], [7], [10]. Таким образом, наша работа встроена в структуру разветвленных хемокинетических сетей, которые рассматривались преимущественно в контексте кинезина [20], [21].Наша цель состоит в том, чтобы напрямую связать экспериментально определенные хемокинетические параметры миозина V, такие как связывание и высвобождение нуклеотидов, с распределениями времени пребывания, измеренными в экспериментах с одной молекулой с двуглавым миозином V .В экспериментах с одной молекулой, в которых задействован двуглавый миозин V, шаги мотора отслеживаются посредством движения бусинки, прикрепленной к ножке мотора. Оценка траектории шага, как показано на рис. 1, приводит к распределению времени его ожидания, в течение которого двигатель находится между двумя шагами.Эти времена пребывания предоставляют информацию о хемомеханическом механизме молекулы и были рассчитаны для кинезина [22] и для сложных сетей миозина V [23]. Для кинезина трудно измерить распределение времени пребывания из-за быстрой кинетики двигателя [24]. Для миозина V, однако, более медленное движение позволяет экспериментально определить общую форму его распределения времени пребывания. Сетевое представление миозина V, представленное в работе. [19] и используемый здесь основан на экспериментально наблюдаемом разделении шкал времени между механическими и химическими переходами [13], [25].Подобное разделение шкалы времени наблюдалось для обычного кинезина [24] и использовалось для построения хемомеханических сетей с несколькими мотоциклами [21], [26], [27]. Рисунок 1. (а) Типичная траектория шага, т.е. пространственное смещение как функция времени и (б) распределение миозина V по времени пребывания, адаптированное из [4].(a) В экспериментах с одной молекулой с петлей обратной связи данные отслеживаются при постоянной внешней нагрузке. Следовательно, расстояние между шариком, контролирующим движение двигателя (верхняя серая траектория, с тонкой черной линией, показывающей отфильтрованную кривую), и центром ловушки (черная траектория) остается постоянным.(б) Распределение времени пребывания миозина V для насыщения [АТФ]. Сплошная линия соответствует модели из работы. [4], который включает две экспоненциальные функции со скоростью затухания 150 / с и 12,5 / с. https://doi.org/10.1371/journal.pone.0055366.g001 Этот документ организован следующим образом. Мы даем краткий обзор сетевых представлений для молекулярных двигателей и формализма для расчета распределений времени пребывания с использованием марковской динамики. Сначала мы описываем кинетику двигателя с помощью одного химико-механического цикла, который доминирует для внешних нагрузок ниже силы срыва, как следует из нашего предыдущего исследования [19], в котором мы использовали более сложную трехтактную сеть.Затем мы вычисляем распределения времени пребывания двигателя для различных концентраций нуклеотидов, что очень хорошо согласуется с экспериментальными данными. Использование сети, основанной на нескольких параметрах, позволяет количественно оценить влияние скорости связывания и высвобождения нуклеотидов на распределения времени пребывания. Во-вторых, принимая во внимание дополнительные пути от более сложной сети, мы количественно определяем стробирующий эффект двигателя. Чтобы обратиться к зависимому от силы распределению времени выдержки, мы обсудим диапазон внешних нагрузок, для которых применяется одноцикловая сеть.Наш подход позволяет нам определять отдельные распределения для шагов вперед и назад, и мы получаем информацию о шагах двигателя назад путем сравнения с экспериментальными данными. Наконец, мы подведем итоги и обсудим наши результаты. МетодыСетевые представительстваВ общем, шаговые свойства молекулярных двигателей могут быть описаны через сетевые представления с дискретными химико-механическими состояниями двигателя, дополненными марковской динамикой. Как объяснялось в предыдущих исследованиях [19], [26], [28], сеть для двуглавого двигателя, как правило, содержит много химических состояний, которые различаются заселенностью двух головок нуклеотидами. Интересно отметить, что каждое из этих химических состояний представляет собой точку разветвления сетей. Как показано в Ref. [19], поведение миозина V, наблюдаемое в экспериментах с одной молекулой, можно описать сокращенными сетками с четырьмя химическими состояниями, как на рис. 2 (а), или с шестью химическими состояниями на рис.2 (б). В этих сетях мотор движется по дискретной одномерной координате к зазубренному концу актиновой нити. Места связывания вдоль нити разделяются размером шага двигателя. На каждом участке двигатель может претерпевать несколько химических переходов, которые приводят либо к гидролизу, либо к синтезу одной молекулы АТФ. Эти переходы соединяют состояния двигателя, которые определяются химическим составом двух его головок. Каждая головка может содержать связанный АТФ (T) или ADP (D), и она может быть пустой (E), так что комбинация этих состояний ведущей и ведомой головки двигателя определяет, вместе с ее положением, его хемомеханическое состояние . .Чтобы определить время задержки между двумя шагами двигателя, мы рассматриваем сеть со всеми химическими состояниями в данном узле решетки с состояниями 3 ′ ′ и 4 ′ на соседних узлах x ′ ′ и x ′. Химический переход из состояния в состояние включает связывание или высвобождение АТФ, АДФ или P, в то время как механические переходы соответствуют шагам вперед и назад по размеру. На протяжении всей работы мы используем сети с поглощающими границами, т.е. е., сетевые представления, которые включают все моторные состояния на узле решетки и усекаются на соседних узлах и.Скорость шага двигателя может быть получена, если цикл сети периодически повторяется вдоль нити накала, см. Рис. 2 (а). Сеть, которая фиксирует шаговые свойства для экспериментально доступного диапазона сил нагрузки, как обсуждается в [19], показана на рис. 2 (b). Это расширенная версия сети на рис. 2 (а) с двумя дополнительными циклами и. Эти два цикла становятся доминирующими для движения двигателя в диапазоне сил, превышающих силу остановки двигателя. Сеть содержит два ступенчатых перехода: в цикл и в цикл.Из этой сети можно вывести скорость шага двигателя, используя несколько копий сети, см. [19]. Здесь мы сосредоточимся на одноцикловой сети, показанной на рис. 2 (а), которая, как подсеть трехтактной сети, описывает движение двигателя для ограниченного диапазона внешних нагрузок. Такой подход позволяет аналитически определять распределения времени пребывания. Более того, может быть установлена прямая связь между скоростью химического связывания и высвобождения мотора и распределением времени пребывания для различных концентраций нуклеотидов.Чтобы извлечь дополнительную информацию, в частности, об эффекте стробирования, мы вернемся к более сложной сети на рис. 2 (b). Хемомеханическая сеть на рис. 2 (а) описывает шаговое поведение миозина V в соответствии с экспериментальными исследованиями [4], [9] для сил, которые не превышают силу срыва двигателя pN. Подробнее о зависимости от внешней нагрузки мы расскажем ниже. Двигатель запускается из состояния DD с ADP, привязанным к обеим головкам, высвобождает ADP из своей задней головки для достижения состояния ED, связывает ATP со своей задней головкой (TD) и выполняет шаг вперед, во время которого обе головки меняют свое положение (DT ).Гидролиз в головной части приводит к состоянию DD, и, таким образом, траектория, соединяющая два химически эквивалентных состояния, завершает химико-механический цикл (DD ED TD DT DD). Обратный цикл (DD DT TD ED DD) приведет к обратному этапу DT TD, связанному с синтезом АТФ. Циклы и образуют сетевой цикл. Эксперименты in vitro обычно проводят для относительно низких концентраций АДФ и Ф, что означает, что как синтез АТФ, так и обратный цикл сильно подавлены.Кроме того, скорость диссоциации АТФ от задней головки V-мотора миозина, которая является частью обратного цикла, очень мала, как подробно обсуждается в [19]. Однако шаги назад все еще возможны, даже для относительно простой сети, показанной на рис. 2 (a), поскольку шаг назад может происходить сразу после шага вперед, соответствующего последовательности TD DT TD. Последняя последовательность переходов очень маловероятна при отсутствии нагрузки, но становится более вероятной с увеличением силы нагрузки [19]. Гейтинг и механические детали шага Myosin VПрежде чем мы обсудим реальную динамику сети, давайте кратко рассмотрим некоторые молекулярные детали миозина V, которые будут важны для того, чтобы связать наши теоретические результаты с экспериментальными наблюдениями. До сих пор мы делали упор на одноцикловую сеть. В этой сети высвобождение АДФ происходит в конце молекулы. Если бы состояние DD было «симметричным» по отношению к высвобождению ADP, вероятность высвобождения ADP из ведущей головки была бы равна таковой из ведомой головки.Однако общепризнано, что скорость высвобождения АДФ различна для ведущей и замыкающей головы [8], [9]. Таким образом, чтобы описать эффект стробирования в явной форме, нам необходимо рассмотреть трехцикловую сеть, показанную на рис. 2 (b). Считается, что разные скорости высвобождения АДФ из головок миозина V возникают из-за внутренних напряжений, которые испытывают головки, когда они одновременно связаны с филаментом [9]. В этом случае одна головка подвергается действию положительной внутренней силы, а другая — отрицательной.Эксперименты с одноголовыми конструкциями миозина V показали, что скорость высвобождения АДФ зависит от направления внешней нагрузки, накладываемой на молекулу [18]. Когда обе головки привязаны к нити, двигатель испытывает внутреннюю деформацию, возникающую из-за упругих свойств его рычагов, что соответствует силе, действующей на обе головки в противоположных направлениях. Однако до какой степени это напряжение распространяется в двуглавом двигателе, априори не ясно. Шаг миозина V состоит из большого направленного поворота его рычага, называемого силовым ударом, и диффузного поиска следующей цели в свободной головке.Упругая энергия, обеспечиваемая силовым ударом, индуцируется гидролитической реакцией, происходящей в миозиновой головке. Однако остается неясным, как эта упругая энергия распределяется в различных химических состояниях моторных головок. В одноголовых молекулах кинетические свойства рабочего удара подробно охарактеризованы [15], [29]. Ход вызывается конформационным изменением, которое влияет на положение головки двигателя на нити и вращает плечо рычага. Предполагается, что это конформационное изменение влияет на состояние двигателя, связанное с АДФ [15].В двуглавой молекуле упругая энергия, необходимая для удара, приводит к напряженному положению миозина V, как было установлено из изображений АСМ, которые показывают изгиб ведущего рычага молекулы [16], тем самым изменяя внутреннюю силу, действующую на моторные головки. Таким образом, и закрытие, и рабочий ход влияют на шаги двигателя. Подшаги миозина V наблюдались в различных экспериментах [6], [7], [13], [25] с разными номерами подшагов и размерами шагов. Имея в виду эти наблюдения, мы объединим предполагаемые подэтапы миозина V в один шаг и обсудим ограничения нашего подхода вместе с зависимостью времени пребывания от внешней нагрузки. Еще одно свойство, которое до конца не изучено, — это эффект стробирования. В экспериментальном исследовании с участием мутантов кинезина-1 возможные причины стробирующего эффекта выясняются с помощью одномолекулярных методов [30]. Авторы заключают, что гейтинг в kinesin-1 возникает как за счет внутримолекулярного напряжения, так и за счет стерических эффектов. Из-за размера шага миозина V 36 нм, который велик по сравнению с размером шага кинезина 8 нм, стерические эффекты стробирования, вероятно, будут играть второстепенную роль для миозина V.Для миозина V как Refs. [5] и [9] пришли к выводу, что внутримолекулярная деформация приводит к увеличению скорости высвобождения АДФ в задней головке молекулы и к снижению скорости высвобождения АДФ в передней головке. Сравнение с данными [18], в которых тестируются отдельные головки как функция силы, подтверждает вывод о том, что высвобождение АДФ из передней головки сильно снижено, в то время как высвобождение в задней головке только умеренно усиливается. Мы характеризуем стробирующий эффект, используя скорость высвобождения АДФ, которая измеряется в хемокинетических экспериментах [3], и накладываем асимметрию за счет снижения скорости высвобождения АДФ в ведущей головке.Несмотря на то, что мы используем здесь конкретную сеть, наш подход применим к любому описанию сети для миозина V, которое позволяет высвобождать АДФ из обеих головок молекулы, например, предложенной в [28]. Однако в целом параметризация будет отличаться для разных сетей, особенно в отношении силовой зависимости скорости перехода. Обратимся теперь к формализму, который позволяет вычислить распределения времени пребывания для миозина V .Цепи МарковаРаспределение вероятности для времени между двумя последовательными шагами двигателя определяется случайным блужданием, которое имеет одну или несколько поглощающих границ.Этот подход соответствует проблеме первого прохода в конкретной сети [31] и тесно связан с методами, используемыми в [22], [23]. Процесс начинается в фиксированном месте и останавливается, когда достигается состояние поглощения. Для цепи Маркова, которая состоит из двух состояний, начального состояния 0 и поглощающего состояния 1, связанных скоростью перехода, распределение вероятностей является экспоненциальным, что применимо к миозину V для сил сопротивления суперстолка. В траекториях, наблюдаемых в экспериментах с одной молекулой, время задержки между двумя последовательными шагами соответствует случайным блужданиям, динамика которых определяется лежащей в основе хемомеханической сетью.Эти случайные блуждания начинаются сразу после механического шага и заканчиваются после другого механического шага. Кроме того, эти состояния также завершают случайное блуждание, когда выполняется шаг через механический переход. Марковская цепь, которая соответствует замкнутой сети, таким образом, состоит из части этой сети, которая содержит все химические переходы в узле решетки и заканчивается на двух соседних узлах, см. Рис. 2 (а). Таким образом, последние два состояния — это , поглощающие состояний сети, а оставшиеся состояния — это переходных . Пусть для данной цепи Маркова с состояниями и первые состояния будут переходными, а остальные состояния — поглощающими. Мы обозначаем условную вероятность того, что процесс останется в состоянии во время, при условии, что он начался в состоянии во времени, через. Соответствующее главное уравнение: (1) где — скорость перехода или скачка из состояния в состояние. Эти скорости имеют общий вид (2) где учитывается силовая зависимость [26]. Для лучшей читаемости мы опускаем штрих для обозначения пространственной координаты как в скоростях перехода, так и в функциях.Для химических скоростей у нас есть (3) вида нуклеотидов X, что соответствует разбавленным растворам. Для скоростей шагов в и, мы имеем (4) для прямого и (5) для обратного шага с параметром в соответствии с условиями баланса из неравновесной термодинамики [27]. В принципе, все скорости химических переходов могут зависеть от силы, но эту зависимость трудно оценить. Силовая зависимость связывания или высвобождения определенного нуклеотида в сложной макромолекуле, такой как моторная головка, не может быть объяснена с помощью основных подходов, таких как теория скорости реакции.Таким образом, наш минимальный подход состоит в том, чтобы пренебречь предполагаемой зависимостью химических скоростей от силы, если такая зависимость не требуется для описания экспериментальных данных. В соответствии с экспериментальными исследованиями [9], [18], мы, таким образом, пришли к выводу в [19], что только скорости связывания и уменьшаются с сопротивлением нагрузкам, см. Раздел S. 2 текста S1 для получения подробной информации о параметризации. Силовой зависимости этих двух скоростей достаточно для описания шагового поведения миозина V для всех трех режимов внешней нагрузки.Таким образом, мы считаем, что все химические скорости не зависят от силы как для цикла в трехцикловой сети на рис. 2 (б), так и для одноцикловой сети на рис. 2 (а). Устойчивое решение главного уравнения задается для любого переходного состояния, потому что прогулка в конечном итоге всегда заканчивается в поглощающем состоянии. Для поглощающего состояния равняется вероятности быть поглощенным при условии, что прогулка началась, см. [22]. Динамика процесса до поглощения идентична динамике неограниченного марковского процесса.Это означает, что до тех пор, пока процесс не переходит в поглощающее состояние, его поведение идентично поведению закрытой сети: находясь в данном состоянии, на процесс не влияют поглощающие состояния, пока процесс не будет завершен. Перед достижением поглощающего состояния случайное блуждание продолжается с экспоненциально распределенным временем ожидания в каждом переходном состоянии (6) со средним временем пребывания. Процесс начинается в состоянии, пребывает в каждом состоянии в соответствии с вероятностью (7), пока в конечном итоге не будет поглощен состоянием.Время ожидания процесса определяется кратчайшим временем, которое требуется для достижения любого поглощающего состояния, учитывая, что прогулка началась, см. Раздел S. 1 текста S1. Для описания траекторий из экспериментов с одной молекулой нас интересуют все блуждания, которые, как упоминалось ранее, начинаются в состоянии непосредственно после механического перехода. Этот переход может состоять из шага вперед или назад, что подразумевает два возможных начальных состояния. Вдобавок, поскольку другой механический шаг в прямом или обратном направлении завершает процесс, у нас также есть два возможных состояния поглощения.Для того, чтобы различать подмножества времен ожидания, которые возникают в результате прямого и обратного шагов, требуется условное распределение плотности вероятности. Это распределение управляет подмножеством прогулок, которые начинаются и поглощаются, и, таким образом, относится к погружению в определенное состояние. Распределение условной плотности вероятности определяется как (8) Он задается зависящей от времени производной вероятности, масштабированной с учетом вероятности устойчивого состояния для поглощения,.Чтобы определить с помощью уравнения. В уравнении (8) мы явно решаем основное уравнение, чтобы получить зависящие от времени вероятности перехода, и, следовательно,. Соответствующее стационарное решение следует интегрированием, (9) Прежде чем обсуждать явный вид распределений времени пребывания, отметим, что в случае сети, которая не содержит каких-либо поглощающих состояний, соответствующее основное уравнение может быть переписано в терминах разностей потоков или избыточных потоков от состояния к состоянию (10) с избыточными потоками и скоростями перехода.Скорость шага двигателя связана с потоком через механические переходы сети в установившемся состоянии с. Для сетевого цикла, показанного на рис. 2 (а), скорость двигателя определяется формулой (11), т. Е. Избыточным потоком через переход. Условное распределение времени задержкиДавайте вычислим распределения, которые относятся к переходам, соединяющим два последовательных шага вперед или назад, и, или шаг назад, следующий за шагом вперед, и наоборот, и.Следовательно, четыре распределения имеют начальные состояния 3 и 4 и поглощающие состояния 3 ′ ′ и 4 ′ соответственно. В химико-механическом цикле скорости диссоциации АТФ и связывания P в случае [P] очень малы, в соответствии с экспериментальными условиями в [4], [7]. Для упрощения мы установили эти скорости равными нулю в наших расчетах, так что путь исчезает в сети на рис. 2 (а). Для сети на рис. 2 (b), состоящей из трех циклов, мы используем значения для скоростей переходов и, как определено в [5].[19], в то время как остальные ставки внутри идентичны для обеих сетей. Вероятности установившегося состояния читаются. (12) (13) (14) (15) С использованием уравнения 8, распределения времени пребывания для этих четырех условных шагов могут быть явно рассчитаны и сравнены с экспериментальными данными. Как показано в [22], распределения, которые относятся к вероятностям выполнения шага вперед и назад, и читаются. (16) (17) (18) Распределение для всех событий дается формулой (19) Распределения и являются многоэкспоненциальными функциями со скоростью затухания, причем хвост распределений определяется наименьшим собственным значением (20) Собственные значения для сети читаются (21) (22) (23) Для малого [ADP] первые два собственных значения уменьшаются до и. РезультатыЗависимость от концентраций нуклеотидовЧтобы сравнить наши результаты с экспериментально определенными распределениями, приведенными в [4], [7], мы изменили масштаб экспериментальных данных таким образом, чтобы область, покрытая гистограммой, была нормализована. В этой статье экспериментальные данные показаны в виде зеленых полос, в то время как распределения общего времени пребывания, полученные из сети, показанной на рис. 2 (а), отображаются в виде сплошных синих линий. В экспериментах [4], [7] использовались низкие концентрации ADP и P, так что мы можем положить [P] равным нулю, как обсуждалось в предыдущем разделе.Для сравнения мы также берем [P] = 0 в трехцикловой сети, однако наши результаты не меняются для [P] = 0,1, концентрации, используемой в [19]. Поскольку связывание ADP оказывает большее влияние на движение двигателя [2], [32], мы используем, если не указано иное, небольшую концентрацию [ADP] = 0,1 в наших расчетах как для одноцикловой, так и для трехтактной сети. . Мы также выполнили расчеты для нулевой концентрации АДФ и проверили, что точное значение [АДФ] не меняет каким-либо существенным образом распределения. На рис. 3 показано общее распределение времен пребывания,, для и различных концентраций нуклеотидов с использованием скоростей переходов, показанных в таблице 1, и экспериментальных данных из [4]. Скорости перехода для трехцикловой сети приведены в работе. [19]. Для, [ATP] = и малого [ADP], см. Рис. 3 (a), наши результаты (синие линии) хорошо согласуются с данными. У нас есть, и хвост распределения отражает скорость выпуска ADP. При добавлении 400 [АДФ] (рис. 3 (b)) распределение значительно расширяется, что отражает ингибирующий эффект АДФ на движение мотора, факт, хорошо установленный экспериментально [2], [6], [32].Для ограничения [АТФ] (рис. 3 (c, d)) скорость шага в отсутствие ADP определяется скоростью связывания ATP. Рис. 3. (a – d) Распределение времени пребывания для различных концентраций АТФ и АДФ, где [P] =, как обсуждается в тексте.Сравнение распределений, рассчитанных с использованием одноцикловой сети на рис. 2 (а) (синие сплошные линии), с экспериментальными данными (зеленые столбцы) из [4]. Вставки: Концентрации, применимые к обеим теоретическим кривым экспериментальных данных, показаны на серых панелях, а параметры, относящиеся к теоретическим результатам, приведены в рамках.В (a), (c – d) экспериментальная концентрация АДФ считается незначительной. Для насыщения [ATP] (a, b) распределения времени выдержки для одноцикловой сети (синяя линия) согласуются с таковыми для сети, показанной в 2 (b), для всех параметров стробирования (данные не показаны). Символы показывают смоделированные данные для сети в 2 (b) без стробирования (зеленые кружки) и стробирования с 10-кратным замедлением высвобождения ADP из ведущей головки двигателя (красные кружки). https://doi.org/10.1371 / journal.pone.0055366.g003 Сеть на рис. 2 (a) не содержит перехода, в котором ADP высвобождается из ведущей головки. Эффект стробирования необходимо учитывать для сетей, в которых используются переходы DD DE или ED EE. Последние переходы составляют утечек из простой сети на рис. 2 (а). Чтобы устранить эффект стробирования, мы также рассмотрели более сложную сеть, которая позволяет высвобождать ADP из ведущей головки, как показано на рис. 2 (b). Он содержит дополнительный шаговый переход вперед и назад и активен в режиме сил сопротивления надстройки, см. Раздел S.2 текста S1. Сети, которые включают выпуск ADP как для ведущей, так и для ведомой головок, могут быть дополнены упрощающим предположением, что эти ставки не различаются. Действительно, распределения времени пребывания, которые получены из сети, показанной на рис. 2 (b), действительно согласуются с экспериментальными данными для высоких концентраций АТФ без какого-либо стробирования. Опишем эффект стробирования соотношением между скоростями высвобождения АДФ из передней и задней головки молекулы, т.е. е., (24) В случае ограничения [АТФ], пренебрегая эффектом стробирования, предполагая равные скорости высвобождения АДФ для обеих головок, т.е.e« приводит к расхождениям между экспериментальными данными и смоделированными временами пребывания (зеленые кружки на рис. 3 (c, d)) для сети на рис. 2 (b). Эти несоответствия для низкого [АТФ] можно понять, потому что переход связывания АТФ, который ограничивает скорость кинетики двигателя, конкурирует с переходом для высвобождения АДФ из ведущей головки,. На движение не влияет, пока конкурирующие переходы в сети имеют небольшую вероятность по сравнению с связыванием АТФ. В отсутствие стробирующего эффекта скорость высвобождения АДФ в 10 раз выше по сравнению со скоростью связывания АТФ на [АТФ], что приводит к меньшему количеству механических шагов через ступенчатые переходы и.Это приведет к увеличению времени пребывания и, следовательно, к более широкому распределению, чем наблюдаемое экспериментально. Ширина этого распределения в первую очередь определяется параметром стробирования и уменьшается с уменьшением. Для хемомеханической сети на рис. 2 (b), которая включает переход ED EE, красные кружки на рис. 3 (c, d) показывают смоделированные времена выдержки, полученные для параметра стробирования, который находится в диапазоне, где мы находим лучшее согласие смоделированных времен пребывания с экспериментальными данными [5], [9]. Для определения оптимального параметра стробирования мы сравнили экспериментальные распределения времени пребывания и полученные из трехцикловой сети для различных значений. На рис. 4 (а) показано среднеквадратичное отклонение RMSD между экспериментальным временем пребывания и смоделированным как функция параметра стробирования для предельных концентраций АТФ, [АТФ] и [АТФ]. Среднеквадратичное отклонение было рассчитано между смоделированными временами выдержки и экспериментальными как. (25) где — время выдержки для эксперимента и моделирования соответственно, а — количество бинов для экспериментальных данных (зеленые столбцы на рис.3 (в, г)). Обратите внимание, что для сравнения мы скорректировали размер ячейки нашего моделирования в соответствии с экспериментальным размером ячейки. Для обеих концентраций RMSD уменьшается с увеличением и достигает насыщения для значений. Чтобы поддерживать поступательное движение миозина V вперед, связывание АТФ задней головкой и высвобождение АДФ из ведущей головки конкурируют за небольшие концентрации АТФ. Для, скорость связывания АТФ достаточно велика по сравнению с высвобождением АДФ из ведущей головки, и RMSD насыщается. Поскольку все другие параметры, используемые для описания скорости V миозина, получены из экспериментальных данных (в пределах), значение следует рассматривать как нижнюю границу для параметра стробирования. Согласие между рассчитанным распределением времени пребывания и экспериментальными данными можно дополнительно улучшить, если рассматривать скорость связывания АТФ в хемомеханическом цикле как подходящий параметр. Рис. 4 (b) показывает распределение времени пребывания для [АТФ] для скорости связывания АТФ, которая обеспечивает наилучшее соответствие для фиксированного параметра стробирования. Вставка на рис. 4 (b) показывает RMSD как функцию переменной скорости связывания АТФ, которая имеет минимум при. Отметим, что при варьировании положение минимума незначительно смещается в пределах диапазона, попадающего ниже.Как можно заключить из фиг. 4 (b), согласие между рассчитанными распределениями времени пребывания и экспериментальными данными можно улучшить, рассматривая скорость связывания АТФ в качестве подгоночного параметра. Для скорости связывания АТФ мы использовали значение, как сообщалось для связанного с актином миозина V в хемокинетических экспериментах с миозином V [3]. Значения связывания АТФ, оцененные из экспериментов с одной молекулой, охватывают диапазон [4], [33]. Так как наилучшее соответствие нашего моделирования данным приводит к скорости связывания АТФ, которая находится в пределах этого диапазона. Зависимость от внешней нагрузкиПрежде чем рассматривать распределение времени пребывания миозина V под действием внешней нагрузки, давайте обсудим скорость шага двигателя как функцию от внешней нагрузки. Соответствующее соотношение силы и скорости необходимо, чтобы прояснить (i) диапазон внешних нагрузок, в котором описание через сеть, образованную циклом, является действительным, а (ii) — набор экспериментальных данных, которые могут быть оценены в рамках наших теоретических расчетов. рамки. Используя скорости перехода, указанные в таблице 1, мы вычисляем скорость (26) двигателя по формуле. 11. Скорость зависит от силы внешней нагрузки и концентраций [АТФ] и [АДФ] через скорости перехода. Далее мы будем различать три различных режима внешней нагрузки: (I) вспомогательные и малые силы сопротивления, где pN; (II) силы, близкие к силе срыва с pN pN; и (III) большие силы сопротивления с pN. На рис. 5 показана скорость двигателя, рассчитанная для одноцикловой сети на рис.2 (a) с периодическими граничными условиями для различных концентраций АТФ, с [ADP] = [P] 0 и соответствующими экспериментальными данными, сообщенными различными группами [1], [6], [7], [10], [34 ]. Экспериментальные значения срывной силы охватывают диапазон 1,6–2,5 пН [1], [6], [7], [10], [34], в то время как 2 пН для сети, исследованной в [1]. [19]. Обратите внимание, что трехцикловое сетевое описание двигателя миозина V в работе. [19] адекватно фиксирует храповой механизм миозина V, наблюдаемый в [10] для больших сил сопротивления (режим (III)), в то время как описание одного цикла, основанное на сетевом цикле, недействительно в этом режиме нагрузки. Рисунок 5. Скорость двигателя как функция внешней нагрузки для сети, образованной циклом (линии), по сравнению с экспериментальными данными (символы) для изменения [ATP].Считается, что в экспериментах концентрации АДФ и Ф довольно малы. В расчетах учитывается предел [ADP] = [P] = 0. https://doi.org/10.1371/journal.pone.0055366.g005 Для насыщения [ATP] сравнение с экспериментальными данными показывает хорошее согласие для малых сил сопротивления в режиме (I).Однако в режиме (II) вокруг срывной силы наблюдается расхождение между теоретическими результатами и экспериментальными данными. Поскольку наша параметризация основана исключительно на параметре для учета силовой зависимости скорости шагов и, молекулярные детали шага не включены в наше описание. Следовательно, распределение времени остановки двигателя нельзя сравнивать с экспериментальными данными для сил, близких к силе срыва. Отметим, что, кроме того, вариация экспериментальных данных ограничивает возможность сравнения всех измеренных распределений времени пребывания в зависимости от внешней нагрузки.Скорости в [5] [7], показанные сплошными голубыми ромбами на рис. 5, соответствуют экспериментальным распределениям времени пребывания, приведенным в них. Распределения для сил pN, pN, pN и pN доступны из Ref. [7], а для pN — из [7]. [4]. Кроме того, распределения времени пребывания для pN можно найти в [7] (используется здесь) и [10]. Сравнение экспериментального распределения времени пребывания с теоретическим имеет смысл, если соответствующая скорость правильно воспроизводит данные, что имеет место для pN и pN.Распределение для pN будет рассмотрено ниже. Поскольку экспериментальные и теоретические результаты для скорости не совпадают для обоих и pN, теоретическое и экспериментальное распределения времени пребывания также не могут совпадать. Расхождение для pN отражает изменение экспериментальных данных, а последнее значение, pN, относится к силовому режиму (II), когда данные не воспроизводятся правильно нашей сетью. Ref. [7] обеспечивает более точное соответствие скоростным данным для сил, не превышающих pN, за счет включения большего количества параметров, зависящих от силы.Однако это не приводит к правильному прогнозированию силы срыва. Это иллюстрирует трудности правильного описания полного набора измеренных распределений времени пребывания. Распределение сил, которые не превышают силу срыва, показано на рис. 6 (a – c) для pN, pN и pN. При наличии внешней нагрузки распределения изменяются в зависимости от силы шага вперед и назад и с коэффициентом силы. Для сил надстройки, изображенных на рис.6 (d), двигатель движется назад принудительно, что может быть описано сетью на фиг. 2 (b), которая содержит состояние EE. Для pN мы находим хорошее согласие между нашими теоретическими результатами и экспериментальными данными, как показано на рис. 6 (а). Это подтверждает, что для вспомогательных сил шаговое поведение практически не изменилось по сравнению с рис. 6 (b), как наблюдалось в [7]. Все теоретические кривые, возникающие из сети на рис. 2 (а), показывают крутой спад быстрых событий на короткие времена 0.01 с. Ширина этого затухающего сигнала увеличивается с увеличением сопротивления нагрузки. Для силы pN, как на рис. 6 (c), ширина этого пика превышает экспериментальное разрешение s [7] (синяя линия). Эти кратковременные события связаны с распределением шагов назад, и отражают увеличение скорости обратного шага с увеличением нагрузки. Однако экспериментальные данные на рис. 6 (c) согласуются с распределением прямых ступенек (пунктирная коричневая линия). Число событий обратного шага, наблюдаемых в [7], могло быть недостаточным для определения распределений.Эти быстрые события также наблюдались при моделировании одноголовых конструкций миозина V [23]. Таким образом, было бы желательно провести экспериментальные исследования, посвященные этим коротким временам простоя, чтобы лучше понять механические свойства двигателя, такие как реверсирование его рабочего хода [15]. В режиме нагрузки (II), близком к силе срыва, параметризации с одним параметром, зависящим от силы, недостаточно для объяснения распределения времени простоя двигателя. Мы изменили масштаб теоретического распределения для pN таким образом, чтобы его максимум соответствовал экспериментальным данным в [5].[7]. Масштабированное распределение и экспериментальное распределение расходятся, что может быть связано с дополнительными переходами, например, теми, которые захватывают подэтапы, вызванные рабочим ходом двигателя, как обсуждалось в контексте эффекта стробирования. Поскольку скорость шага двигателя уменьшается в экспериментах медленнее, чем в нашей теории, можно предположить, что механические свойства молекулы стабилизируют ее химическую активность в присутствии внешней силы. Частично этот эффект стабилизации объясняется пороговым значением силы при параметризации химических скоростей, см. Раздел S.2 текста S1 и [19], который обеспечивает правильное воспроизведение храпового поведения миозина V, но не влияет на механический шаг мотора сам по себе. Из-за недостатков нашей модели для сил вокруг силы срыва, соответствующей силовому режиму (II), кажется правдоподобным ожидать, что эффекты в скорости механических шагов, возникающие из-за рабочего хода двигателя, также должны быть приняты во внимание для описания медленное снижение скорости с увеличением нагрузки. При высоких силах сопротивления, pN, двигатель работает принудительно с одной частотой шага, как определено в Ref.[19] на основе данных [10]. Для сверхустановленных сил механический цикл управляет движением молекулы в силовом режиме (III), так что двигатель проходит исключительно через переход. В этом случае распределение времени выдержки сводится к экспоненциальной функции со скоростью / с для pN, как показано на рис. 6 (d) в соответствии с данными. DiscussionВ этой статье мы сосредоточились на сетевом описании миозина V, которое состоит только из четырех хемомеханических состояний, и рассчитали распределения времени пребывания для этого молекулярного мотора.Наш подход обеспечивает прямую связь между скоростью связывания и высвобождения нуклеотидов, которая доступна в хемокинетических экспериментах, и распределениями времени пребывания, наблюдаемыми при измерениях одиночных молекул миозина V. Распределения времени пребывания, полученные из нашего сетевого описания, согласуются с экспериментальными данными для широкого диапазона концентраций нуклеотидов, рис. 3, и сил подстилающей нагрузки, рис. 6 (a – c). В случае малых концентраций АДФ хвосты распределений регулируются для насыщения [АТФ] скоростью высвобождения АДФ и скоростью связывания АТФ для малых концентраций АТФ.Сравнение с более сложной сетью (Рис. 2 (b)) позволяет нам выяснить эффект стробирования, см. Рис. 3 (c, d). В сетях, которые включают высвобождение АДФ из ведущей головки, связывание АТФ конкурирует с высвобождением АДФ из этой головки. Значительное влияние на скорость шага двигателя возникает, когда две скорости перехода имеют сопоставимую силу; скорость двигателя снижается выпуском ADP. Эффект стробирования приводит к регулированию этого торможения за счет подавления скорости высвобождения АДФ из передней головки двигателя по сравнению с его задней головкой.Путем сравнения с экспериментальными данными мы количественно оцениваем эффект стробирования по скорости высвобождения АДФ, которая различается в 10 раз для ведущей и ведомой головки двигателя. В случае силы внешней нагрузки, действующей на двигатель, мы определили диапазон сил, который может быть описан через сеть, состоящую из четырех состояний, путем анализа соотношения силы и скорости миозина V, рис. 5. Кроме того, мы различаем распределения времени задержки, возникающие при обратном и прямом шагах двигателя.Для промежуточных сил сопротивления экспериментальные данные согласуются с распределением времени выдержки, которое связано с шагами вперед. Пик для коротких событий может быть связан с шагом назад, см. Рис. 6 (c). Наш анализ сильно подкрепляет гипотезу о том, что движение двигателя регулируется для сил, вплоть до силы срыва, простым химико-механическим циклом, а не сложной разветвленной сетью, которая координируется зависимым от силы высвобождением АДФ. Следующий шаг — связать информацию о быстрых событиях с рабочим ходом двигателя. . |



