Для чего нужен дифференциал: что это, значение, принцип работы

Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?

Давайте начнем с дифференциала, а точнее с производной, потому что о ней речь заходит у всех еще в школе. Из школьного определения мы знаем «Производная это отношение приращения функции к приращению аргумента». Проще говоря это отношение изменения функции к изменению аргумента, но эта фраза тоже может быть понятна не всем. Функция это некая величина, которая меняется в некоторой зависимости от другой величины — аргумента. Таким образом производная показывает нам во сколько раз функция изменяется быстрее (или медленнее), чем аргумент. Теперь уточним что такое «приращение». Вообще производная это отношение дифференциалов, а дифференциал некоторой величины это бесконечно малое ее изменение, то есть разница между некоторым начальным и конечным значением, только эти значения мы берем максимально близко друг к другу, как бы изучая изменение функции на каждом максимально маленьком ее участке. Самое очевидное приложение в естественно научной области это описание зависимости изменения расстояния, пройденного некоторым объектом от времени. Разделив бесконечно малое изменение расстояния на соответствующий ему бесконечно малый момент времени (dS/dt, где буква d обозначает что мы берем не абсолютные величины а дифференциалы) мы получим так называемую мгновенную скорость, то есть скорость, которую имел объект в конкретный момент времени. Естественно что эта скорость в другой момент времени может отличаться и тут уже находит свое приложение интеграл. Интегрируя какое то дифференциальное уравнение мы проводим суммирование по некоторой переменной. Обращаясь к нашему примеру со скоростью проинтегрировав по dt в определенных пределах (эти пределы это тоже значения времени но уже не бесконечно близко стоящие друг к другу а какие то реальные, пусть от 0 секунд до 60, например) мы получим среднюю скорость объекта, которую он имел на протяжении этой минуты. Приложение дифференциалов и интегралов в естественных науках невероятно велико и данный пример с скоростью движения просто простейшая иллюстрация, переоценить вклад этого математического аппарата в естественные науки невозможно.

Вообще дифференциально-интегральные исчисления это огромная часть математики именуемая математическим анализом, она несет в себе гораздо гораздо больше чем я написал, это целые курсы лекций как на естественно-научных специальностях, так и на непосредственно математических. Добавлю так же что описное мной выше станет гораздо понятнее если обратится к какому нибудь учебнику, наверное даже, по школьной физике или математике, в котором будут графики зависимости расстояния от времени и на них будут схематично изображены дифференциалы, там же должны быть приведены схожие с моими рассуждения.

Для чего нужен дифференциал. Дифференциал. Назначение и основные типы. Устройство повышенного сопротивления

Его основное предназначение заключается в распределении, изменении и передачи крутящего момента, а при необходимости, для обеспечения вращения двух потребителей с различными угловыми скоростями.

Межколесный дифференциал – это дифференциал, предназначенный для привода ведущих колес, если же он установлен между ведущими мостами в полноприводном автомобиле – межосевой интервал.

Как правило, дифференциал автомобиля располагается в следующим местах:

• Привод ведущих мостов в полноприводном автомобиле – в раздаточной коробке
• Привод ведущих колес в полноприводном автомобиле – в картере заднего и переднего моста
• Привод ведущих колес в переднеприводном автомобиле — в коробке передач
• Привод ведущих колес в заднеприводном автомобиле – картер заднего моста

В основе дифференциала лежит планетарный редуктор. Используемый в редукторе вид зубчатой передачи условно делит дифференциал на три следующих вида:

• Червячный
• Цилиндрический
• Конический

Червячный – самый универсальный дифференциал и может быть установлен как между осями, так и между колесами. Цилиндрический тип, как правило, располагается в автомобилях между осями. Конический тип применяется в основном как межколесный.

Различают также несимметричный и симметричный дифференциалы автомобиля. Несимметричный тип устанавливается между двумя приводными осями и позволяет передавать крутящий момент в различных пропорциях.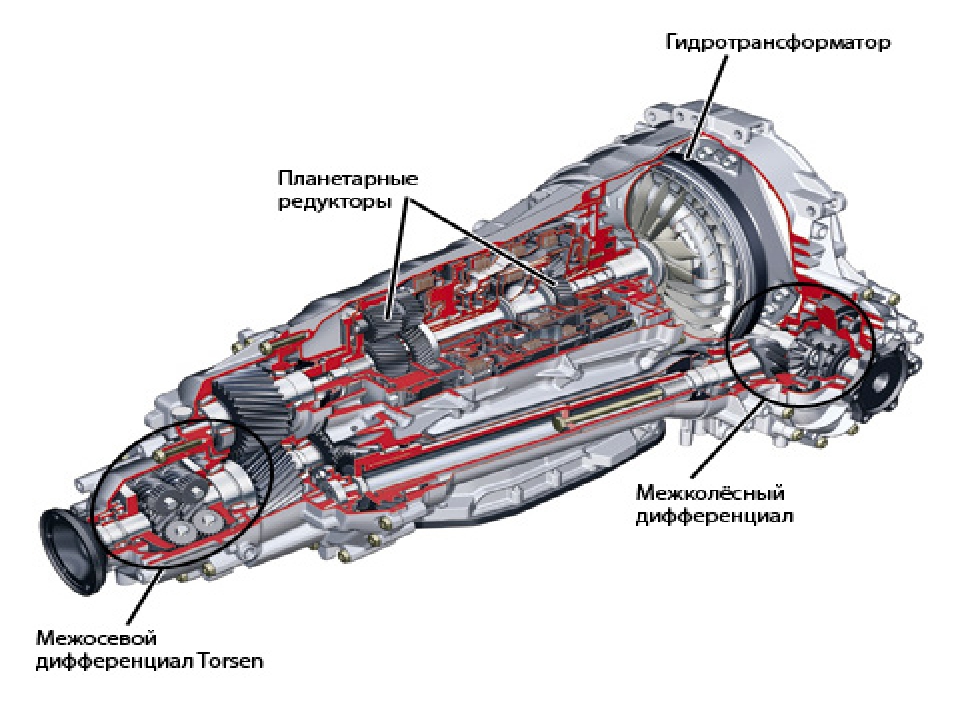 Симметричный тип, как правило, устанавливается на главных передачах и позволяет передает на два колеса равный по значению крутящий момент.

Устройство автомобильного дифференциала

Основными элементами дифференциала являются:

• Полуосевые шестерни
• Шестерни сателлитов
• Корпус

Схема дифференциала переднеприводного автомобиля:

1 — ведомая шестерня главной передачи; 2 — фрагмент ведущей шестерни главной передачи; 3 — ось сателлитов; 4 — сателлит; 5 — корпус дифференциала; 6 — правый фланцевый вал; 7 — сальник; 8 — конический роликовый подшипник; 9 — полуосевая шестерня; 10 — левый фланцевый вал; 11 — фрагмент картера коробки передач.

Шестерни сателлитов по своему принципу работы напоминают планетарный редуктор и служат для соединения между собой корпуса и полуосевой шестерни. Последние в свою очередь соединяются с помощью шлицов с ведущими колесами. В различных конструкциях используются четыре или два сателлита, в легковых автомобилей чаще используется второй вариант.

Чашка дифференциала или корпус – ее основное предназначение заключается в том, чтобы передавать через сателлиты крутящий момент от главной передачи к полуосевым шестерням. Внутри него располагаются оси для вращения сателлит.

Солнечные или полуосевые шестерни – предназначены для передачи крутящего момента с помощью полуосей на ведущие колеса. Левая и правая шестерни могут иметь как одинаковое, так и различное между собой число зубцов. В свою очередь шестерни с различным число зубов используются для образование несимметричного дифференциала, а с одинаковым количеством – для симметричного.

Принцип работы автомобильного дифференциала

Работает дифференциал следующим образом: вращая одно из ведущих колес автомобиля, второе начнет вращаться в противоположном направлении, но при этом должно выполняться условие неподвижности карданного вала. В данном случае стеллиты вращаются в свих осях, играя роль шестерни.

Если завести двигатель и включить сцепление и любую из передач, начнет свое вращение карданный вал, передающий свой крутящий момент через цилиндрические и конические шестерни коробке дифференциала.

Таким образом, во время движения автомобиля по кривой траектории одно колесо замедляет свой ход, второе наоборот увеличивает его. В результате устраняется пробуксовка и скольжение колес и каждое из них вращается с той скоростью, которая необходима для безопасного движения.

Во время движения автомобиля по прямой, ничего особенного не происходи и дифференциал передает крутящий момент на оба колеса в одинаковом соотношении. Шестерни полуосевые вращаются с одинаковой угловой скоростью, так как сателлиты в этом случае находятся в неподвижном состоянии.

При движении на скользких покрытиях дифференциал обладает одним существенным недостатком – он может вызвать боковой занос машины, так как на буксующем колесе низкая сила сцепления с покрытием и оно начинает вращаться в холостую.

Самые простейшие дифференциалы автомобиля обладают еще одним недостатком. При попадании грязи или прочих сторонних элементов между шлицами крутящий момент может передаваться в различном соотношении, даже 0 к 100.

Таким образом, одно колесо останется в абсолютно статичном положение.

Современные модели практически лишены данного недостатка. Их устройство отличается ручной или автоматической более жесткой . Более того, во многих легковых современных машинах устанавливаются системы стабилизации и курсовой устойчивости, позволяющие оптимизировать в зависимости от траектории движения автомобиля распределение крутящего момента.

Как работает дифференциал — видео:

На этом всё, теперь вы знаете устройство дифференциала.

Многие, кто собрался приобретать внедорожник, при выборе определённой модели, конечно могли столкнуться с термином «блокировка дифференциала». Но что это? Как это? И каков принцип работы и надобность этого самого дифференциала? Как показывает практика, знают не все будущие потенциальные «джиповоды».

В этой статье мы расскажем о том, что из себя представляет дифференциал

и зачем он в автомобиле. Каких разновидностей он бывает и на какие автомобили предусмотрена его установка?

История дифференциала

Появление дифференциала в автомобильном мире не заставило себя ждать. Спустя лишь несколько лет, после того, как с конвейера стали сходить первые автомобили с двигателем внутреннего сгорания (ДВС). Давно ведь дело обстояло не так сладко, как сейчас и первые автомобильные образцы, которые работали при помощи двигателя, очень плохо управлялись.

Колёса, расположенные на одной оси, во время поворота вращались с одинаковой угловой скоростью, а это уже приводило к тому, что колесо, идущее по внешнему диаметру, сильно пробуксовывало. Решили эту проблему достаточно просто: заимствованием дифференциала у паровых повозок.

Этот механизм был изобретён во Франции в 1828 году инженером Оливером Пекке-Ром. Это было устройство, которое состояло из валов и шестерней. Через него крутящий момент от ДВС передавался на ведущие колёса.Но вот случилась ещё одна незадача – стали пробуксовывать колёса, которые утрачивали сцепление с дорожным покрытием. Зачастую это проявлялось во время движения по дороге с обледенелыми участками.

Колесо, которое находилось на льду, вращалось с большей скоростью, чем колесо, что оставалось на более пригодной для движения поверхности. Это и приводило к заносу. После конструкторы и стали думать о том, как настроить дифференциал, чтобы колёса вращались с одинаковой скоростью, дабы воспрепятствовать появлению заносов.

Первым человеком, проводившим эксперименты над дифференциалом с минимальным проскальзыванием, стал ни кто иной как Фердинанд Порше. Для того, чтобы рынок повидал кулачковый дифференциал – «детище» Порше с ограниченным проскальзыванием, потребовалось не менее трёх лет. Им оснащали первые модели автомобилей марки . В следующие десятилетия инженерами были разработаны разнообразные виды дифференциалов, о которых мы расскажем Вам далее.

Принцип работы и устройство

Давайте, пожалуй, начнём с типа дифференциала, который является самым простым для рассмотрения – открытого дифференциала. Мы начнем с простейшего типа дифференциала, называемого открытым дифференциалом. Итак, конструкция дифференциала включает в себя следующие части:

— Ведущий вал. Его задача заключается в передаче крутящего момента. Вал ведёт его от трансмиссии к самому началу дифференциала.

— Ведущая шестерня ведущего вала. Шестерня в форме косозубого конуса, необходимая для сцепки дифференциальных механизмов.

— Коронная шестерня. Элемент, являющийся ведомым. Так же имеет форму конуса и вращается ведущей шестернёй. Система вместе взятых ведущей и ведомой шестерней называется главной передачей. Она служит на завершающем этапе по уменьшению скорости вращения, которое достигает колёс в конечном счёте.

Ведущая шестерня в своих размерах гораздо уступает коронной , поэтому для осуществления одного оборота ведомой, первой необходимо совершить не один оборот вокруг своей оси.

— Шестерни полуосей. Являются последним рубежом передачи вращения ведущего вала колёсам.

— Сателлиты – это планетарный механизм, осуществляющий ключевую роль в обеспечении разной угловой скорости колёс при осуществлении поворота.

Когда Вы двигаетесь по прямой на своём автомобиле, то весь дифференциальный механизм вращается с единой скоростью: входной вал вращается с идентичной скоростью, что и полуоси, соответственно, с той же скоростью происходит и вращение самих колёс. Но только Вы повернёте руль, ситуация моментально в корне изменяется. Главными игроками теперь

выступают сателлиты, которые разблокировываются под воздействием разности нагрузок на колёса , когда, например, одно колесо начинает пробуксовывать и поэтому движется быстрее.

Вся мощность мотора проходит непосредственно через них. А в результате того, что сателлиты представляют из себя две шестерни, которые независимы, то происходит передача разной частоты вращения двум полуосям. Но мощность не разделяется поровну, а передаётся на колесо, что движется во внешнем крае поворота машины . Следовательно оно и начинает крутиться гораздо быстрее за счёт количественного прибавления оборотов. И разность в распределении мощностей между колёсами тем больше, чем меньше радиус поворота автомобиля, то есть чем сильнее Вы выворачиваете рулевое колесо.

Что такое блокировка дифференциала и как она работает

Блокировка дифференциала – это один из эффективнейших способов повышения внедорожных характеристик автомобиля.

Любой автомобиль, который предназначается напрямую или косвенно для бездорожья, оснащается конструкторами на заводе механизмом, который блокирует межосевой дифференциал. Так же автомобили оснащают механизмами, блокирующими передний и задний мосты.

Блокировка данного механизма, как и любое технологическое решение имеет свои преимущества и недостатки. Чтобы понять, когда необходимо использовать блокировку дифференциалов, а какие случаи просто запрещают её использование, нужно разобраться в принципах, на которых её действие основывается.

Попробуйте в зимнее заснеженное время совершить с места прыжок в длину. Ага. А вот и не получается, а всё потому, что одна нога у вас оказалась на скользкой оледенелой поверхности, а вторая на сухом асфальте. Вот из-за этого и не получилось совершить чемпионский прыжок. Одна нога выскользнула из под Вас, а мозг не сориентировался вовремя и не дал команду вложить всю силу для толчка в другую ногу. Итог этого эксперимента достаточно весел и комичен: ноги разъехались и Вы чуть не рухнули на пятую точку.

Так что же сделать в данном случае, чтобы обе ноги возымели возможность прекрасно оттолкнуться от земли? А всё очень и очень просто. Необходимо просто две толчковые ноги превратить в одну, связав их прочно между собой прочным ремнём или жгутом. Теперь они будут работать, как одно целое и будет использоваться максимальная сила толчка от одной стабильной опорной поверхности с хорошим сцеплением. Аналогичный процесс происходит и в автомобиле в момент взаимодействия его ведущих колёс с дорогой.

Давайте представим ситуацию при которой заднеприводный автомобиль остановился случайным образом так, что его левое колесо оказалось на скользкой поверхности, а правое на асфальте. Как Вам известно, стандартный межосевой дифференциал малого трения , который находится на заднем мосту автомобиля, всегда предоставляет колёсам равную окружную силу. Левое колесо, находящееся на льду, не в состоянии сдвинуться со скользкой поверхности с применением больших усилий в силу недостаточности сцепления.

И-за этого дифференциал не в состоянии предоставить ему огромное усилие, так как это просто невозможно физически. А в этом случае аналогичная сила подведётся и к колесу , которое находится на асфальтированной поверхности. Он выровняет усилия, которые распределены между колёсами, ориентируясь на левое колесо.

В результате машина сдвинется с места с пробуксовкой, но медленно. Его колёса не смогут использовать достаточную для толчка силу, которая была бы необходима для сцепления правого колеса, которая в данных условиях будет ни много, ни мало, а в целых семь раз превышающую чем у левого. Из-за такого свойства распределять тяговую силу поровну, правое колесо будет использовать лишь седьмую часть его возможностей сцепления с асфальтом. Говоря проще, толчок мог бы случиться в семь раз мощнее, но дифференциалом не было подведено к нему достаточного количества силы для совершения этого манёвра.

Следовательно необходимо осуществить такую связь между колёсами, для обеспечения совместного вращения или пробуксовки, буд-то бы единого колеса. Для решения данной задачи используется специальный механизм, блокирующий вращение шестерней дифференциала и связывающий два колеса между собой условной жёсткой связью с постоянным вращением и одинаковой скоростью. Такой механизм называется «механизм блокировки (отключения) дифференциала», или в простонародье – блокировкой.

Дифференциал, что заблокирован не в состоянии выравнивать межколёсное усилие, тем самым делая их связанными единой осью. В результате чего каждое колесо получает максимально возможную силу, которая нужна для наилучшего сцепления колёс. Следовательно, где лучше сцепление колёс с дорожной поверхностью, туда и будет прилагаться большая сила.

Какие бывают дифференциалы

Основой дифференциала является планетарный редуктор. Вид зубчатой передачи, который используется, условно может разделить дифференциал на три вида:

— Червячный;

Цилиндрический;

Конический.

Червячный дифференциал является самым универсальным и устанавливается как между осями, таки между колёсами. Цилиндрический тип, зачастую, располагается во внедорожниках меж осей. Конический тип в основном применяется в качестве межколёсного дифференциала.

Выделяют так же симметричный и несимметричный дифференциалы. Несимметричная конструкция дифференциала устанавливается в полно приводных автомобилях между осями, распределяя крутящий момент в различных пропорциях. Симметричный тип передаёт на ось между двумя колёсами равный крутящий момент. Так же дифференциалы разделяют по виду блокирования: ручная блокировка и электронная блокировка.

Ручная блокировка дифференциала

Исходя из названия, блокировка дифференциала оси включается по инициативе водителя с помощью нажатия кнопки или переключения определённого тумблера. В данном случае происходит блокировка шестерней-сателлитов, в результате чего ведущие колёса начинают вращаться с одинаковой скоростью. Зачастую ручной блокировкой дифференциала оснащаются внедорожники. Включать её рекомендуется для преодоления тяжёлого бездорожья, а отключение производить при выезде на обычную асфальтированную дорогу.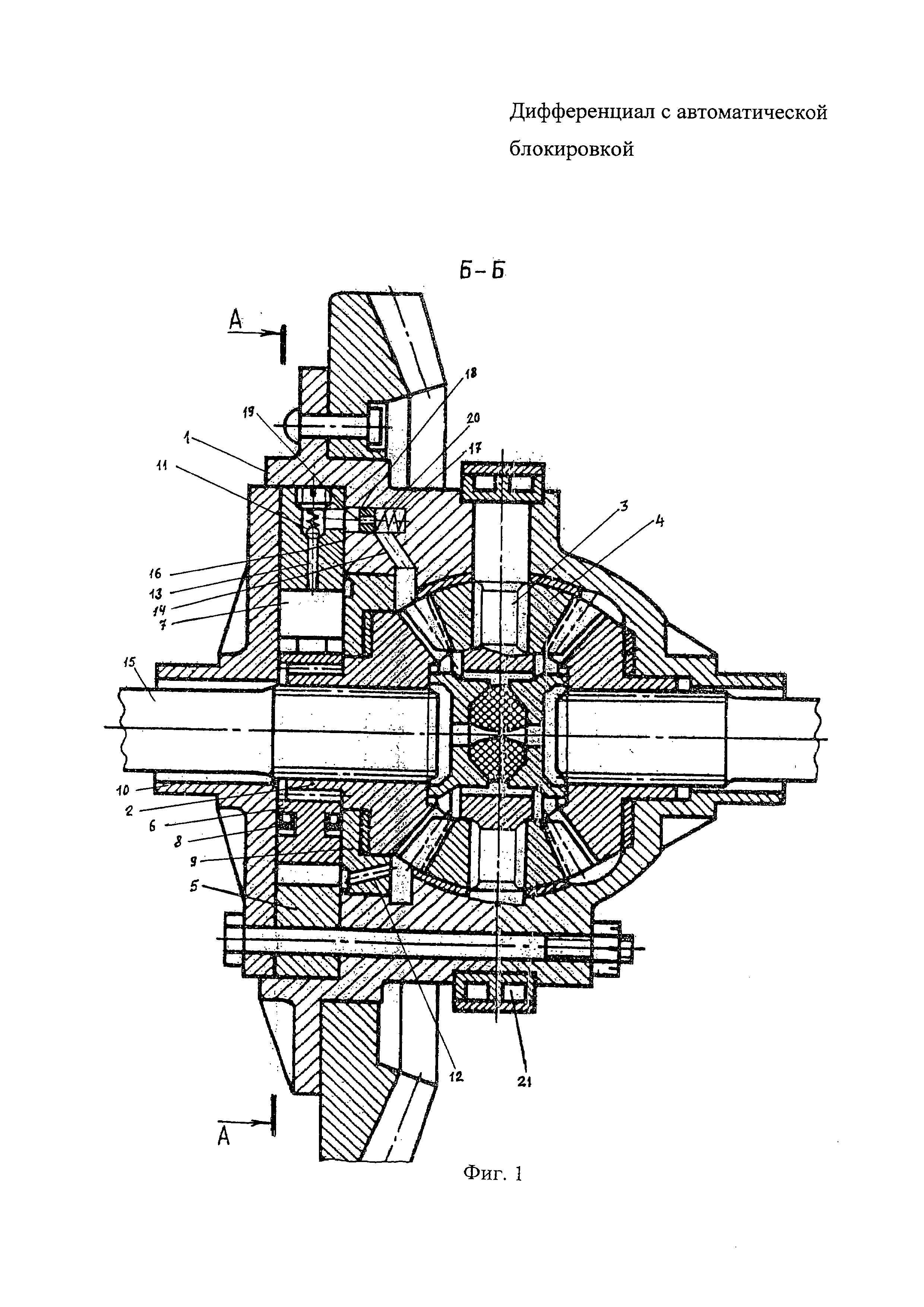

Электронная или автоматическая блокировка дифференциала

Автоматическое блокирование дифференциала осуществляется путём команд электронного блока управления, который анализирует состояние, в котором находится дорожное покрытие, используя ABSи ESP. Затем ЭБУ самостоятельно блокирует шестерни-сателлиты. По степени блокирования это устройство можно условно подразделить на дифференциал с полной и частичной блокировками.

Полная блокировка дифференциала

Включение такой блокировки подразумевает под собой тот факт, что шестерни-сателлиты останавливаются полностью, а механизм берётся за выполнение функций обычной муфты, тем самым передавая равностепенный крутящий момент на две полуоси. Вследствие этого оба колеса вращаются с одинаковой угловой скоростью. Если случится то, что хотя бы одно колесо потеряет сцепление с поверхностью, то крутящий момент с него в полной мере передаётся на другое колесо, которое осталось форсировать бездорожье. Такое дифференциальное устройство успешно реализовано на Toyota Land Cruiser, Mercedes-Benz G-Class и других.

Частичная блокировка дифференциала

Включение этой блокировки не полностью останавливает шестерни-сателлиты, а позволяет им проскальзывать. Такой эффект доступен благодаря самоблокирующимся дифференциалам. В зависимости от типа срабатывания данного механизма, делят его на два вида: Speed sensitive (задействуется, когда замечается разница в угловых скоростях вращения полуосей) и Torque sensitive (задействуется в случае уменьшения крутящего момента одной полуоси).Такой тип срабатывания дифференциального устройства можно встретить на внедорожниках Mitsubishi Pajero, Audi Q-серии и BMW X-серии.

Группа дифференциалов Speed sensitive различается строением конструкции. Одним из таких механизмов является тот, в котором дифференциальную функцию выполняет вискомуфта. Вискомуфта отличается от фрикционного дифференциала своей меньшей надёжностью. Именно из-за этого она имеет место устанавливаться на автомобили, которые не предназначены для преодоления непролазных дебрей и глубоких бродов или на автомобили со спортивным характером.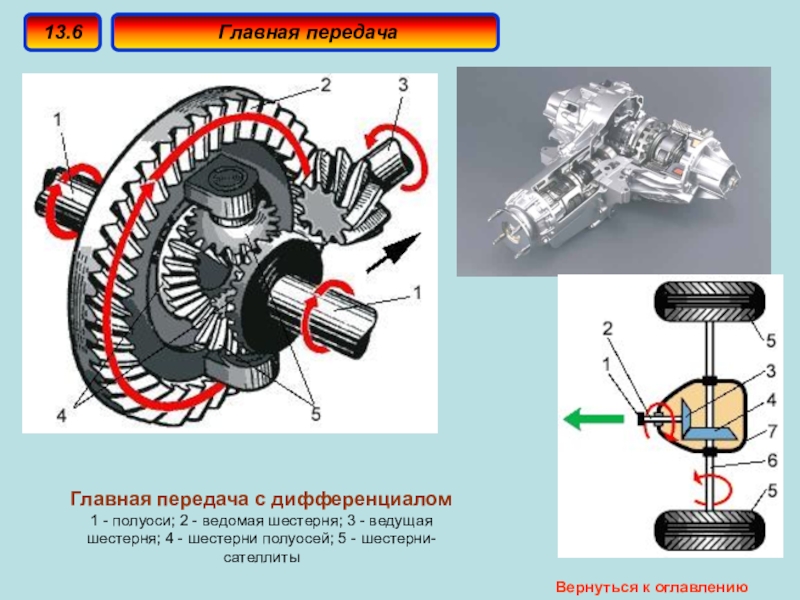

Ещё один механизм представляющий группу Speed sensitive называется героторный дифференциал. Роль блокирующих элементов здесь играют масляный насос и фрикционные пластины, монтируемые между корпусом дифференциала и шестернями-сателлитами полуосей. Хотя по принципу действия он схож с вискомуфтой.

Дифференциалы, которые относятся к группе Torque sensitive , также различны по своей конструкции. Например есть механизм с использованием фрикционного дифференциала. Особенность его заключается в разности угловых скоростей колёс в поворотах и при движении по прямой. Когда автомобиль движется по прямой, угловая скорость вращения обоих колёс одинакова, а во время прохождения поворота, крутящий момент для колёс различен.

Очередной тип дифференциалов — с гипоидным и косозубым зацеплением. Они условно подразделяются на три группы.

Первая – с гипоидным зацеплением

Здесь каждая полуось имеет свои собственные шестерни-сателлиты. Крепятся они между собой путём прямозубого зацепления, располагаясь перпендикулярно друг относительно друга.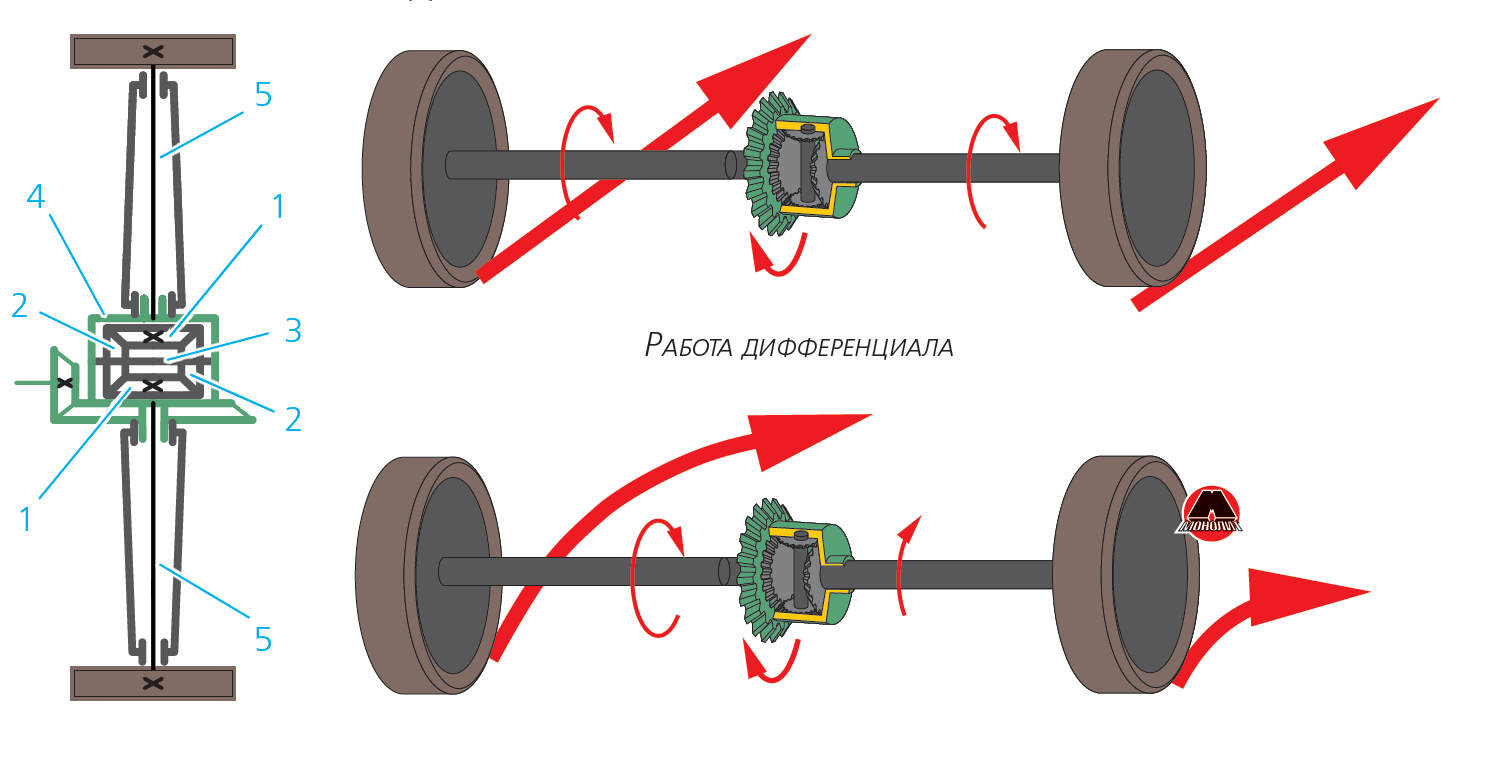 В случае возникновения разницы угловых скоростей ведущих колёс, происходит расклинивание шестерней полуосей. В результате чего шестерни трутся о корпус дифференциала. Дифференциал частично блокируется и происходит перераспределение крутящего момента на ось, с меньшей скоростью углового вращения. После выравнивания полуосевых скоростей, блокировка деактивируется.

Вторая – с косозубым зацеплением

Аналогична первой, но расположение шестерен-сателлитов параллельно относительно полуосей. Эти агрегаты крепятся между собой путём косозубого зацепления. Сателлиты этого механизма вмонтированы в специальные ниши на корпусе дифференциала.Когда наблюдается различие в угловой скорости колёсного вращения, шестерни расклиниваются и сопрягаются с шестернями, что находятся в нишах дифференциального корпуса. Происходит частичная блокировка. Направление крутящего момента определяется на ось с меньшей скоростью вращения.

Третья – с косозубыми шестернями полуосей и винтовыми шестернями сателлитов

Используется в межосевых дифференциалах. Принцип тот же – смещение крутящего момента на ось с меньшим вращением. Диапазон смещения этого вида достаточно велик — от 65/35 до 35/65. Когда угловая скорость колёсного вращения обоих осей стабилизируется и выравнивается, дифференциал разблокировывается. Эти дифференциальные группы широко применяются в автомобилестроении как на обычных моделях, так и на спортивных.

Преимущества и недостатки блокировки дифференциалов

+ возможность колёсного блокирования до 70%;

Минимальное обслуживание;

Отсутствие рывков на руле;

КПП не требует заливания специального масла;

Установка не влечёт никаких сложностей;

Обеспечение лучших внедорожных характеристик автомобиля;

Более длительный срок работы конструкции;

Лучшая управляемость автомобиля;

Способность прохождения поворотов на более высоких скоростях;

Автомобиль легче выводится из заноса.

По истечению времени падает преднатяг;

Требуется замена регулировочных элементов каждые 40 тысяч километров для лучшей работоспособности конструкции;

Не своевременное или запоздалое проведение регулировочных работ приведут к тому, что система будет работать не корректно.

Подписывайтесь на наши ленты в

Дифференциал предназначен для передачи, изменения и распределения крутящего момента между двумя потребителями и обеспечения, при необходимости, их вращения с разными угловыми скоростями.

Дифференциал является одним из основных конструктивных элементов трансмиссии . Расположение дифференциала в трансмиссии автомобиля:

Дифференциалы, используемые для привода ведущих колес, называются межколесными. Межосевой дифференциал устанавливается между ведущими мостами полноприводного автомобиля.

Конструктивно дифференциал построен на основе планетарного редуктора. В зависимости от вида зубчатой передач, используемой в редукторе, различают следующие виды дифференциалов: конический, цилиндрический и червячный.

Конический дифференциал применяется в основном в качестве межколесного дифференциала. Цилиндрический дифференциал устанавливается чаще между осями полноприводных автомобилей. Червячный дифференциал, ввиду своей универсальности, может устанавливаться как между колесами, так и между осями.

Устройство дифференциала рассмотрено на примере самого распространенного конического дифференциала. Составные части дифференциала являются характерными и для других видов дифференциалов. Конический дифференциал представляет собой планетарный редуктор и включает полуосевые шестерни с сателлитами, помещенные в корпус.

Корпус (другое наименование – чашка дифференциала) воспринимает крутящий момент от главной передачи и передает его через сателлиты на полуосевые шестерни. На корпусе жестко закреплена ведомая шестерня главной передачи. Внутри корпуса установлены оси, на которых вращаются сателлиты.

Сателлиты, играющие роль планетарной шестерни, обеспечивают соединение корпуса и полуосевых шестерен. В зависимости от величины передаваемого крутящего момента в конструкции дифференциала используется два или четыре сателлита. В легковых автомобилях применяется, как правило, два сателлита.

Полуосевые шестерни (солнечные шестерни) передают крутящий момент на ведущие колеса через полуоси, с которыми имеют шлицевое соединение. Правая и левая полуосевые шестерни могут иметь равное или различное число зубьев. Шестерни с равным числом зубьев образуют симметричный дифференциал, тогда как неравное количество зубьев характерно для несимметричного дифференциала.

Симметричный дифференциал распределяет крутящий момент по осям в равных соотношениях, независимо от величины угловых скоростей ведущих колес. Благодаря этим свойствам симметричный дифференциал используется в качестве межколесного дифференциала.

Несимметричный дифференциал делит крутящий момент в определенном соотношении, поэтому устанавливается между ведущими осями автомобиля.

Работа дифференциала

В работе симметричного межколесного дифференциала можно выделить три характерных режима:

1. прямолинейное движение;
2. движение в повороте;
3. движение по скользкой дороге.

При прямолинейном движении колеса встречают равное сопротивление дороги. Крутящий момент от главной передачи передается на корпус дифференциала, вместе с которым перемещаются сателлиты. Сателлиты, обегая полуосевые шестерни, передают крутящий момент на ведущие колеса в равном соотношении. Так как сателлиты на осях не вращаются, полуосевые шестерни движутся с равной угловой скоростью. При этом частота вращения каждой из шестерен равна частоте вращения ведомой шестерни главной передачи.

При движении в повороте внутреннее ведущее колесо (расположенное ближе к центру поворота) встречает большее сопротивление, чем наружное колесо. Внутренняя полуосевая шестерня замедляется и заставляет сателлиты вращаться вокруг своей оси, которые в свою очередь увеличивают частоту вращения наружной полуосевой шестерни. Движение ведущих колес с разными угловыми скоростями позволяет проходить поворот без пробуксовки. При этом, в сумме частоты вращения внутренней и наружной полуосевых шестерен всегда равна удвоенной частоте вращения ведомой шестерни главной передачи. Крутящий момент, независимо от разных угловых скоростей, распределяется на ведущие колеса в равном соотношении.

При движении по скользкой дороге одно из колес встречает большее сопротивление, тогда как другое проскальзывает — буксует. Дифференциал, в силу своей конструкции, заставляет вращаться буксующее колесо с увеличивающейся скоростью. Другое колесо при этом останавливается. Сила тяги на буксующем колесе, по причине низкой силы сцепления, мала, поэтому и крутящий момент на этом колесе тоже мал. А так как дифференциал у нас симметричный, то на другом колесе крутящий момент тоже будет небольшим. Тупиковая ситуация – автомобиль не может сдвинуться с места.

Для продолжения движения необходимо увеличить крутящий момент на свободном колесе. Это осуществляется с помощью

Многие покупатели при выборе внедорожника наверняка сталкивались в описании той или иной модели с термином «электронная блокировка дифференциала». Но что это такое, и как работает этот самый дифференциал, знают далеко не все потенциальные владельцы автомобилей этого класса. В нашем сегодняшнем материале мы подробно расскажем, для чего машине дифференциал, каковы его разновидности и на какие автомобили он устанавливается.

На фото самоблокирующиеся дифференциалы

История создания и назначение дифференциала

На автомобилях, оснащенных двигателем внутреннего сгорания, дифференциал появился через несколько лет после их изобретения. Дело в том, что первые экземпляры машин, приводимых в действие двигателем, имели очень плохую управляемость. Оба колеса на одной оси при повороте вращались с одинаковой угловой скоростью, что приводило к пробуксовке колеса, идущего по внешнему, большему, чем внутренний, диаметру. Решение проблемы было найдено просто: конструкторы первых автомобилей с ДВС позаимствовали у паровых повозок дифференциал – механизм, изобретенный в 1828 году французским инженером Оливером Пекке-Ром. Он представлял собой устройство, состоящее из валов и шестерней, через которые крутящий момент от двигателя передается на ведущие колеса. Но после установки на автомобиль дифференциала обнаружилась еще одна проблема – пробуксовка колеса, утратившего сцепление с дорогой.

Обычно это проявлялось, когда автомобиль двигался по дороге, покрытой участками льда. Тогда колесо, попавшее на лед, начинало вращаться с большей скоростью, чем то, которое находилось на грунте или бетоне, что в итоге приводило к заносу автомобиля. Тогда конструкторы задумались об усовершенствовании дифференциала с тем, чтобы при подобных условиях оба колеса вращались с одинаковой скоростью и автомобиль не заносило. Первым, кто проводил эксперименты с созданием дифференциала с ограниченным проскальзыванием, стал Фердинанд Порше.

Ему понадобилось три года, чтобы разработать, протестировать и выпустить на рынок так называемый кулачковый дифференциал – первый механизм с ограниченным проскальзыванием, который устанавливался на первые модели марки Volkswagen. Впоследствии инженеры разработали различные виды дифференциалов, о которых речь пойдет ниже.

В автомобиле дифференциал выполняет три функции: 1) передает от двигателя к ведущим колесам, 2) задает колесам разные угловые скорости, 3) служит в сочетании с главной передачей.

Устройство дифференциала

Усовершенствованный автомобильными конструкторами дифференциал устроен в виде планетарной передачи, где крутящий момент от двигателя передается через карданный вал и коническую зубчатую передачу на корпус дифференциала. Тот, в свою очередь, направляет крутящий момент на две шестерни, а уже они распределяют момент между полуосями. Сцепление между шестернями-сателлитами и полуосями имеет две степени свободы, что позволяет им вращаться с разными угловыми скоростями.

Таким образом, дифференциал обеспечивает разную скорость вращения колес, расположенных на одной оси, что предотвращает и пробуксовку при повороте. После того, как был изобретен , у автомобиля появилось два, а впоследствии и три (с межосевым) дифференциала, которые распределяли крутящий момент между ведущими осями.

Уже понятно, что без дифференциала не обходится ни один автомобиль. В передне- и заднеприводных автомобилях он расположен на ведущей оси. Если у автомобиля сдвоенная ведущая ось, то здесь в конструкции трансмиссии применяют два дифференциала — по одному на каждую ось. В полноприводных машинах дифференциалов два (для моделей с подключаемым полным приводом – по одному на каждую ось) или три (для моделей с постоянным полным приводом – по одному на каждую ось, плюс межосевой дифференциал, который распределяет крутящий момент между осями). Кроме количества механизмов, устанавливаемых на автомобили с разными типами приводов, дифференциалы различают по виду блокировки.

Разновидности дифференциалов

По виду блокировки дифференциалы делятся на два – ручная и электронная блокировка. Ручная, как следует из названия, производится водителем вручную при помощи кнопки или тумблера. В этом случае шестерни-сателлиты механизма блокируются, ведущие колеса двигаются с одинаковой скоростью. Обычно ручная блокировка дифференциала предусмотрена на внедорожниках.

Электронная или автоматическая блокировка дифференциала осуществляется при помощи электронного блока управления, который, анализируя состояние дорожного покрытия (используется информация с датчиков и антипробуксовочной системы), сам блокирует шестерни-сателлиты.

Задний дифференциал с электронным управлением Range Rover Sport

По степени блокировки это устройство делится на дифференциал с полной блокировкой и дифференциал с частичной блокировкой шестерен-сателлитов.

Полная блокировка дифференциала предполагает 100%-ную остановку вращения шестерен-сателлитов, при которой сам механизм начинает выполнять функцию обычной муфты, передавая равнозначный крутящий момент на обе полуоси. Вследствие этого оба колеса вращаются с одинаковой угловой скоростью. Если же одно из колес теряет сцепление с дорогой, весь крутящий момент передается на колесо с лучшим сцеплением, что позволит преодолеть бездорожье. Такое устройство дифференциала используется на внедорожниках , и других.

Частичная блокировка дифференциала предполагает неполную остановку вращения шестерен-сателлитов, то есть с проскальзыванием. Достигается такой эффект за счет так называемых самоблокирующихся дифференциалов. В зависимости от того, каким образом срабатывает этот механизм, их делят на два вида: Speed sensitive (функционируют при разнице в угловых скоростях вращения полуосей) и Torque sensitive (функционируют при уменьшении крутящего момента на одной из полуосей). Такое устройство дифференциала используется на внедорожниках Mitsubishi Pajero, Audi с , BMW с системой X-Drive и так далее.

Дифференциалы, относящиеся к группе Speed sensitive, имеют разную конструкцию. Существует механизм, в котором роль дифференциала играет вискомуфта. Она представляет собой резервуар, расположенный между полуосью и ротором карданного вала, заполненный специальной вязкой жидкостью, в которую, в свою очередь, погружены диски, сочлененные с полуосью и ротором. Когда угловая скорость вращения колес разнится (одно колесо вращается быстрее другого), диски в резервуаре тоже начинают вращаться с разными скоростями, но вязкая жидкость постепенно выравнивает их скорость, и, соответственно, крутящий момент. Как только угловые скорости обоих колес сравняются, вискомуфта отключается. По своим характеристикам вискомуфта менее надежна, чем фрикционный дифференциал, поэтому ее устанавливают на машины, предназначенные для преодоления бездорожья средней степени или спортивные модификации автомобилей.

Еще один механизм дифференциала, относящийся к группе Speed sensitive – героторный дифференциал. Здесь роль блокировки, в отличие от вискомуфты, играет масляный насос и фрикционные пластины, которые монтируются между корпусом дифференциала и шестерней-сателлитом полуосей. Но принцип действия во многом схож с таковым у вискомуфты: при возникновении разницы в угловых скоростях ведущих колес насос нагнетает масло на фрикционные пластины, которые под давлением блокируют корпус дифференциала и шестерню полуоси до тех пор, пока скорости вращения колес не сравняются. Как только это происходит, насос перестает работать и блокировка отключается.

Дифференциалы, относящиеся к группе Torque sensitive, тоже имеют разную конструкцию. К примеру, есть механизм, в котором используется фрикционный дифференциал. Его особенностью является разность угловых скоростей вращения колес при движении автомобиля на прямой и в повороте. При езде по прямой дороге угловая скорость обоих колес одинаковая, а при прохождении поворота ее значение различно для каждого колеса. Это достигается за счет установки между корпусом дифференциала и шестерней-саттелитом фрикциона, который способствует улучшению передачи крутящего момента на колесо, утратившее сцепление с дорогой.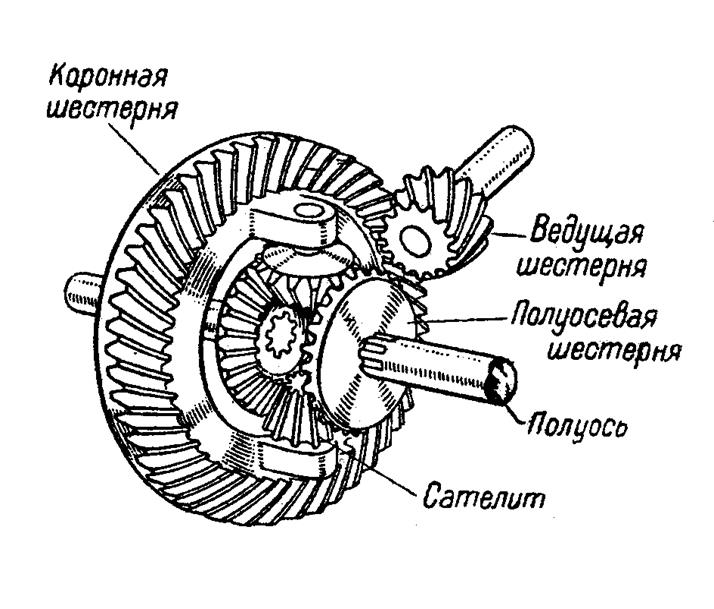

Еще один тип дифференциалов — с гипоидным (червячным или винтовым) и косозубым зацеплением. Их условно делят на три группы.

Первая – с гипоидным зацеплением, в которой у каждой полуоси есть собственные шестерни-сателлиты. Они объединятся между собой при помощи прямозубого зацепления, причем ось шестерни располагается по отношению к полуоси перпендикулярно. При возникновении разницы в угловых скоростях ведущих колес, шестерни полуосей расклиниваются, образуется трение между корпусом дифференциала и шестернями. Происходит частичная блокировка дифференциала и крутящий момент передается на ту ось, угловая скорость вращения которой меньше. Как только угловые скорости колес выровняются, происходит деактивация блокировки.

Вторая – с косозубым зацеплением, в которой у каждой полуоси также есть свои шестерни-сателлиты (они винтовые), но их оси располагаются параллельно полуосям. А объединяются эти агрегаты между собой при помощи косозубого зацепления. Сателлиты в этой механизме установлены в специальных нишах на корпусе дифференциала. Когда угловая скорость вращения колес различается, происходит расклинивание шестерен, и они, сопрягаясь с шестернями в нишах корпуса дифференциала, частично блокируют его. При этом крутящий момент направляется на ту полуось, скорость вращения которой меньше.

Третья – с косозубыми шестернями полуосей и винтовыми шестернями сателлитов, которые располагаются параллельно друг другу. Такой тип используется в конструкции межосевого дифференциала. Благодаря планетарной конструкции дифференциала, имеется возможность посредством частичной блокировки смещать крутящий момент на ту ось, угловая скорость вращения колес которой меньше. Диапазон такого смещения весьма широк – от 65/35 до 35/65. При установлении равнозначной угловой скорости вращения колес передней и задней оси дифференциал разблокируется.

Эти группы дифференциалов получили самое широкое применение в автомобилестроении: их устанавливают как на «гражданские» модели, так и на спортивные.

Дифференциал как автомобильный механизм скоро отметит двухвековой юбилей, однако его конструкция за эти долгие годы хоть и совершенствовалась, но сохранила ключевые особенности. Что же такое дифференциал, и какую роль он выполняет в автомобиле?

1. Что такое дифференциал?

Д ифференциал в автомобиле – это механизм, который позволяет передавать мощность и, следовательно, вращение от коробки передач к колесам, разделяя поток этой мощности на два, для каждого из колес одной оси, с возможностью изменять соотношение передаваемой к ним мощности, и, следовательно, позволяя колесам вращаться с разной скоростью. Проще говоря, дифференциал разделяет 100% мощности, передаваемой коробкой передач, на два потока для каждого из колес на одной оси, и эти потоки могут перераспределяться в зависимости от условий движений от 50:50 до 100:0.

2. Для чего нужен дифференциал?

Основное предназначение дифференциала – обеспечить возможность вращения колес на одной оси с разной скоростью с сохранением неразрывного потока крутящего момента. Для автомобиля это важно прежде всего в поворотах: ведь при движении по дуге колеса на внешней стороне поворота проходят больший путь, чем колеса на внутренней, а значит, должны вращаться с большей скоростью для сохранения стабильности машины.

Если же колеса на оси будут соединены жестко, то внутреннее колесо в повороте будет пробуксовывать. Для заднеприводного автомобиля это повышает риск заноса, а для переднеприводного радикально ухудшает управляемость и контроль автомобиля в повороте. Таким образом, обеспечение свободного и независимого вращения колес на одной оси с сохранением постоянства передачи на них крутящего момента от двигателя было одной из принципиальных задач с момента создания автомобиля – и это задача была успешно решена.

3. Как устроен дифференциал?

Дифференциал являет собой частный случай планетарной передачи. Физически он обычно представляет собой набор из четырех шестерней, вращение к которым передается пятой – ведомой шестерней главной передачи, объединенной с корпусом дифференциала, выполняющим роль водила. Главная передача – это набор из двух шестерней: ведущая получает вращение от КПП и передает его ведомой. Ведомая же шестерня главной передачи передает вращение через корпус на шестерни-сателлиты, а они, в свою очередь, находятся в зацеплении с солнечными шестернями, жестко закрепленными на приводных полуосях колес.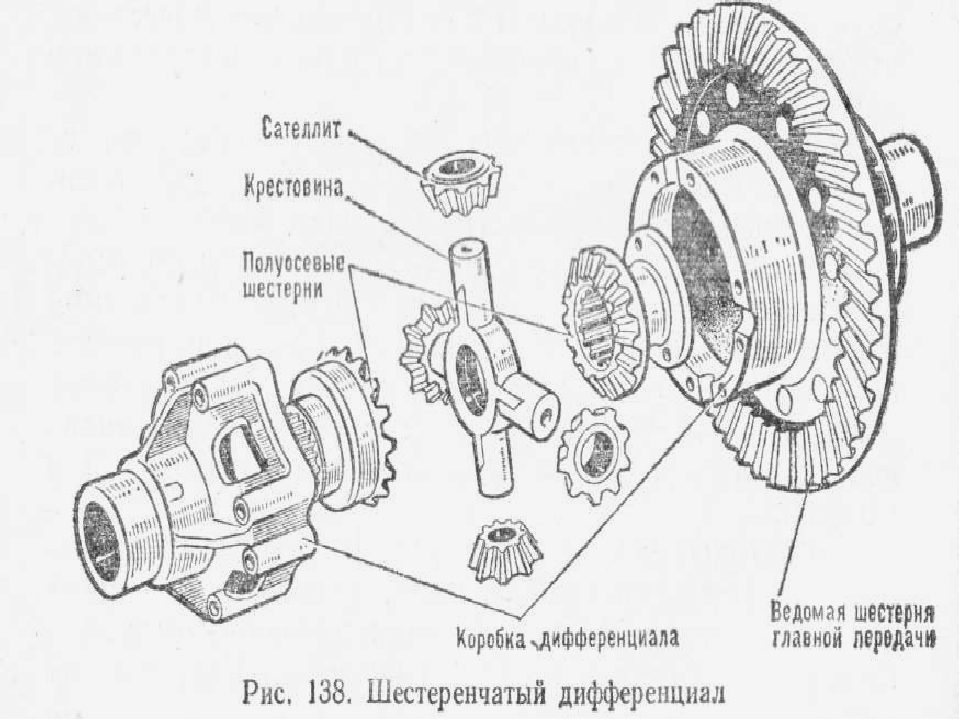

Когда автомобиль движется по прямой, шестерни-сателлиты неподвижны, и скорость вращения шестерни главной передачи равна скоростям вращения солнечных шестерней: колеса вращаются с одинаковой скоростью. В повороте же шестерни-сателлиты начинают вращаться, обеспечивая разницу скоростей солнечных шестерней и, следовательно, колес на внешней и внутренней стороне поворота.

4. Каковы недостатки дифференциала?

Главным недостатком дифференциала одновременно является его главное преимущество – возможность передавать до 100% мощности на одно из колес. Исходя из этого, в условиях, когда одно колесо имеет недостаточное сцепление с поверхностью, основная часть мощности будет передаваться именно на него. Таким образом, порой даже имея одно колесо на поверхности с достаточным сцеплением, автомобиль не может тронуться с места.

Для устранения этой проблемы были разработаны разнообразные конструкции – дифференциалы с повышенным внутренним сопротивлением (так называемые самоблоки) и дифференциалы с принудительной блокировкой, ручной или автоматизированной. В зависимости от конструкции и назначения они могут как изменять перераспределение потока мощности в пользу колеса с хорошим сцеплением с поверхностью, так и полностью замыкать дифференциал, заставляя колеса на оси вращаться с одинаковой скоростью. Разные типы таких дифференциалов мы рассмотрим в отдельных материалах.

Главная передача и дифференциал автомобиля

Расскажем про устройство главной передачи и для чего нужен дифференциал автомобиля. Как происходит обслуживание и основные неисправности в работе.

Для чего нужны

Крутящий момент от коленвала двигателя заднеприводной машины через сцепление, коробку передач и карданную передачу передается на пару косозубых шестерен, которые находятся в постоянном зацеплении. Оба колеса будут вращаться с одинаковой угловой скоростью. Но ведь поворот автомобиля невозможен, т.к. колеса должны пройти неодинаковое расстояние при этом маневре! Внешнее от центра поворота колесо проходит путь значительно больший, чем внутреннее.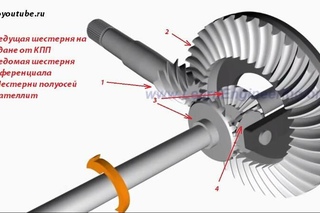

Если бы каждому колесу передавалось одинаковое количество оборотов, то поворот автомобиля, без черных следов, был бы невозможен. Следовательно, любой автомобиль имеет некий механизм, позволяющий ему делать повороты без «черчения» резиной колес по асфальту. Этот механизм называется – дифференциалом.

Дифференциал автомобиля предназначен для распределения крутящего момента между полуосями ведущих колес при повороте автомобиля и при движении по неровностям дороги. Дифференциал позволяет колесам вращаться с разной угловой скоростью и проходить неодинаковый путь без проскальзывания относительно покрытия дороги.

Иными словами 100% крутящего момента, который приходит на дифференциал, могут распределяться между ведущими колесами 50 х 50 или в другой пропорции (например, 60 х 40). К сожалению, пропорция может быть — 100 х 0. Значит одно из колес стоит на месте, а другое буксует. Зато данная конструкция позволяет автомобилю поворачивать без заноса, а водителю не менять каждый день изношенные шины.

Из чего состоит

• двух шестерен полуосей
• двух шестерен сателлитов

Главная передача с дифференциалом: 1 — полуоси; 2 — ведомая шестерня; 3 — ведущая шестерня; 4 — шестерни полуосей; 5 — шестерни-сателлиты.

У переднеприводных автомобилей главная передача и дифференциал расположены в корпусе коробки передач. Двигатель у таких автомобилей расположен не вдоль, а поперек оси движения, значит, изначально крутящий момент от двигателя передается в плоскости вращения колес. Поэтому нет необходимости изменять направление крутящего момента на 90^О, как у заднеприводных машин. Но, функция увеличения крутящего момента и распределения его по осям колес, остается неизменной.

Основные неисправности

Шум («вой» главной передачи) при движении на большой скорости возникает из-за износа шестерен, неправильной их регулировке или при отсутствии масла в картере главной передачи. Для устранения неисправности необходимо отрегулировать зацепление шестерен, заменить изношенные детали, восстановить уровень масла. Подтекание масла может быть через сальники и неплотные соединения. Для устранения неисправности следует заменить сальники, подтянуть крепления.

Как происходит обслуживание

Шестерни главной передачи и дифференциала требуют смазки. Хотя детали выглядят массивными «железяками», но тоже имеют запас прочности. Поэтому рекомендации относительно резких стартов и торможений, грубых включений сцепления и прочей перегрузки машины остаются в силе.

Трущиеся детали и зубья шестерен должны постоянно смазываться. Поэтому в картер заднего моста (у заднеприводных авто) или в картер блока – коробка передач, главная передача, дифференциал (у переднеприводных авто), заливается масло, уровень которого необходимо периодически контролировать. Масло, в котором работают шестерни, имеет склонность к «утеканию» через неплотности в соединениях и через изношенные сальники.

При возникновении подозрений на какую-либо неприятность с трансмиссией, поднимите домкратом одно из ведущих колес автомобиля. Запустите двигатель и, включив передачу, заставьте вращаться это колесо. Просмотрите и прослушайте всё, что крутится, издает подозрительные звуки. Затем поднимите домкратом колесо с другой стороны. При повышенном шуме, вибрациях и подтеканиях масла – ищите сервис.

LSD дифференциал — что это, для чего нужен и как работает

LSD дифференциал — что это, как работает и какую помощь может оказать на бездорожье? Дифференциал повышенного трения LSD работает также, как и аналогичные автоматические неполные блокировки. Он срабатывает в тех случаях, когда колеса на одной оси начинают крутиться со слишком разной по отношению друг к другу скоростью. Чаще всего LSD дифференциал ставят на внедорожники и спортивные автомобили, но считать его 100% блокировкой от застревания в грязи или диагонального вывешивания ошибочно.

LSD дифференциал — что это такое

Как уже было сказано выше, дифференциал повышенного трения LSD не обеспечивает полной блокировки, допуская определенную разницу между скоростями вращения валов. Он срабатывает лишь в том случае, когда разница ощутима. Выше уже было сказано, что LSD часто ставят в различные автомобили: как в спортивные, так и во внедорожники
В пример можно привести LSD дифференциал Toyota — в определенный момент блокировка срабатывает и крутящий момент обеих валов сравнивается, становится одинаковым. Равные пропорции всё равно дают возможность завязшему колесу прокручиваться, но то колесо, которое имеет хорошее сцепление, тоже начинает крутиться и джип выезжает с засады на нормальное место (во многих, но далеко не во всех случаях).

Как работает LSD дифференциал и какие типы бывают
Классический — дифференциал чувствителен к разнице скоростей между валами, блокируя при определенном моменте. Это классическая блокировка, аналогичная вискомуфте. Применяется всё чаще, особенно во внедорожниках, так как лёгок в обслуживании и крайне прост по своей конструкции и принципу действия;

Традиционный — дифференциал срабатывает при разнице между передачей крутящего момента. Его уже почти никуда не устанавливают, встречается только на старых авто и то, чаще в нерабочем или полумертвом состоянии. Дифференциал LSD такого типа можно отнести к червячному типу, он блокирует автоматом при определенной разнице между КМ самого дифференциала и, непосредственно приводного вала.

Классический задний дифференциал LSD очень популярен, но на многих старых машинах доведен до ужасного состояния. В новые его тоже периодически устанавливают, но, как уже говорилось выше, его эффективность в серьезной грязи не очень высока. Многое зависит от прокладки между сиденьем и рулем, поэтому в умелых руках автомобиль лишь с такой блокировкой тоже способен на небольшие подвиги, но заменить 100% блокировку он не способен.

Также начинающие джиперы часто интересуются, как определить LSD дифференциал — делается это очень просто: задняя сторона машины домкратиться так, чтобы колеса отрывались от земли. Передняя часть авто при этом стоит на земле (не забывайте ставить под колеса противооткаты и держать авто на передаче в момент подъема). Колесо, которое оказывается в воздухе, можно попробовать покрутить. Если второе колесо крутится в ту же сторону, то у вас установлен LSD. Если второе колесо начинает крутиться в другую сторону, то в мосту или ничего нет, или дифференциал с блокировкой сломан и не функционирует. Также определить наличие или отсутствие LSD в мосту можно по наклейкам на самом узле или на арке водительской двери, но как показывает практика, чаще всего на старых авто такие наклейки не сохраняются.

LSD (англ. Limited slip differential) — Дифференциал ограниченного проскальзывания/повышенного трения.

Содержание

[править] Общая информация

Принцип действия LSD моста заключен в том, что имеется пакет фрикционных дисков которые через один цепляются то за полуось то за корпус дифа. Диски сжаты пружиной и проскальзывают друг относительно друга с определенным усилием. Вот это усилие и не дает колесу, потерявшему связь с дорогой бешено крутиться в то время как второе стоит на месте.

Подобная схема имеет весьма ограниченные возможности даже близко не приближаясь к 100% — ой блокировке. При этом, данный тип дифа очень капризен к качеству применяемого масла. В любом случае, масло должно быть строго для редукторов с LSD. В противном случае, фрикционы быстро засаливаются и перестают что либо блокировать. Возможно, именно с этим связано то обстоятельство, что большинство подобных дифов на подержанных машинах уже ничего не блокируют.

Проверить это можно следующим образом: включив нейтральную передачу и вывесив одно из колёс, пытаемся покрутить его. По усилию, необходимому для проворота можно судить о степени убитости системы LSD. Чем оно больше, тем лучше. Если же колесо крутиться свободно — частичная блокировка полностью мертва.

Иногда фрикционы можно тщательно помыть бензином и немного оживить. Чаще же, придется менять.

[править] Устройство LSD

В стандартном дифференциале, когда одно из колес теряет сцепление с дорогой, вся мощность и крутящий момент передается именно на это колесо, тогда как другое бездействует. Основная идея блокировки дифференциала — распределение мощности между колесами, когда одно из колес «теряет дорогу». Существует множество различных блокировок, число которых входит и дифференциал повышенного трения L.S.D. limited-slip differential).

Собственно существует несколько основных типов дифференциалов повышенного трения:

• REACTIVE LSD
• PLATE CLUTCH LSD
• CONE CLUTCH LSD
• FERGUSON LSD(Viscous LSD)
• DIRECTIONAL LSD
• LOCKER LSD
• GLEASON (TORSEN) LSD
• QUAIFE LSD

Рассмотрим дифференциал, состоящий из сборки фрикционных дисков и колец, которые несут фунциональную нагрузку по распределению мощности между колесами.

Дифференциал с LSD:

Состоит из двух частей скрепленных болтами. Крышка и основная часть, внутри которой есть четыре большие проточки параллелные линии оси. Крышка крепится болтами к зубчатому венцу ведущей шестерни.

Эта шестерня в LSD слегка отличается от стандартной. Во-первых по центру проточена «звездочка», в которую вставляется конец оси, а во-вторых есть 6 проточек по наржному диаметру для установки фрикцоннных дисков и колец.

• Прижимные кольца (Pressure Rings)

Два больших кольца которые устанавливаются в корпусе дифференциала.

Почти не отличается от стандартного. Устанавливается на оси со специальным профилем (установка на сечение B-B на рисунке ниже), входит в зацепление с шестернями полуосей.

Как сказано выше, на оси крепятся сателлиты (сечение B-B), но кроме этого средняя часть имееет прлоскости (сечение C-C), и единственное отличие от стандартной — это наличие V-образного профиля на концах (сечение A-A). Этот профиль нужен для установки прижимных колец.

• Фрикционные диски (Friction Disks)

Эти диски имеют отверстие с 6 вырезами для крепления на шестерне полуоси. Изготавливаются из стали и имеют различную толщину 1.5 мм, или 1.6 мм.

• Фрикционные кольца (Friction Plates)

Кольца выглядят как диски, только имеют 4 выступа на внешней стороне. Эти выступы входят в пазы на корпусе дифференциала. По толщине идентичны фрикционным дискам.

• Пружинные диски и кольца (Spring Disks and Spring Plates)

Некоторые LSD имеют их, а некоторые нет. Они такие же как фрикционные диски и кольца — единственное отличие — те плоские а эти слегка вогнутые. Техническое название пружина Бельвиля (Belleville spring). Основное назначение сделать работу LSD более эффективной. Когда эта система установлена, то сборка состоит из пары диск-кольцо на каждой стороне.

Рисунок ниже показывает, как соединены фрикционные кольца, диски, придавливающие диски и шестерни полуосей.

• Последовательность сборки

• Фрикционное кольцо или пружинное кольцо
• Фрикционный диск или пружинный диск
• Фрикционное кольцо
• Фрикционный диск
• Фрикционное кольцо
• Фрикционный диск
• Прижимное кольцо (заштриховано)
• Шестерня полуоси (не показано на рисунке)
• Оси сателлитов с сателлитами (центр рисунка)
• Шестерня полуоси (не показано на рисунке)
• Прижимное кольцо (заштриховано)
• Фрикционный диск
• Фрикционное кольцо
• Фрикционный диск
• Фрикционное кольцо
• Фрикционный диск или пружинный диск
• Фрикционное кольцо или пружинное кольцо

[править] Принцип действия

Основа — взаимодействие дисков и колец. Диск крепится к шестерне полуоси, а кольцо на корпусе дифференциала. Если шестерня полуоси крутится со скоростью, иной чем, скорость корпуса дифференциала (он приккреплен к зубчатому венцу ведущей шестерни) то возникает вращение дисков между кольцами. Принцип трения в связке диск-кольцо-масло и положен в основу действия LSD.

Причем сопротивление скольжению пропорционально приложенной силе, чем больше сила тем больше сопротивление.

Одним словом в обычном режиме передача силы происходит по схеме ведущая шестерня -> зубчатый венец, прикрепленный к корпусу дифференциала, и фрикционные кольца, которые тоже соединенны с корпусом. Прижимные кольца вращаются вместе корпусом дифференциала, и передают вращение на оси сателлитов, те в свою очередь на сателлиты, а сателлиты на шестерни полуосей.

Соответственно при потере сцепления одного колеса с дорогой возникает разница скоростей между дисками и кольцами. Давление прижимает фрикционные диски к кольцам, и как следствие увеличивается сопротивление скольжению. Если в вашем LSD нет пружин Бельвиля (Belleville spring plates and disks), то срабатывание будет происходить внезапно, а применение этого механизма делает блокировку более плавной.

[править] Техника ремонта и восстановления

• Разблокирующее давление (Breakaway Pressure)

Разблокирующее давление определяется крутящим моментом необходимым для того чтобы диски и кольца начали скользить. На практике, это момент который образуется во время пробуксовки колес. Если приложите крутящий момент на одну ось, а другую ось заблокируете на месте, то эта ось не будет крутиться до достижения определенного давления. Затем ось начнет крутиться.

Собственно говоря сама эта операция проводится лишь на спортивных машинах и зависит от ряда причин: от колес, которые будут установлены, до настройки подвески. Настройка осуществляется специальными проставками причем их толщина меняется на десятые доли миллиметра. Так же имеет значение толщина фрикционных дисков и колец. В обычной машине используются стандартные диски и кольца.

Как и в любом деле необходимо соблюдать очередность и собственно говоря разборка производится по обратному сборке алгоритму приведенному выше.

[править] LSD 1 way/1.5 way/2 way

Многие производители дифференциалов повышенного трения делят свою продукцию в соответствии с режимом работы на 1 way, 1.5 way и 2 way. Это деление зависит от вида разреза в камере под ось сателлитов (Сателлит — зубчатое колесо планетарной передачи с подвижной осью вращения). Форма разреза непосредственно влияет на работу дифференциала.

1 way означает, что из-за формы разреза блокировка дифференциала происходит только при ускорении. Дифференциал с индексом 2 way блокируется как при ускорении, так и при торможении. Дифференциал 1.5 way также как и 2 way блокирует и при ускорении и при замедлении, но блокировка при замедлении имеет более «мягкий» характер. Этот тип обеспечивает «щадящую» блокировку при торможении и лучше всего подходит для новичков, и менее эффективен, чем 2 way в профессиональном автоспорте. Самое эффективное применение данного типа — это ведущая ось переднеприводного автомобиля.

• Применение типа 1.5 way целесообразнее всего на автомобилях для дорог общего пользования. Более мягкая блокировка при торможении позволяет плавно «смещать» автомобиль в повороте при замедлении (чем при использовании типа 2 way).

• Применение типа 2 way обеспечивает оптимальную блокировку при ускорении и замедлении. Идеально подходит для дрифтинга, особенно для пилотов, которые предпочитают постоянную блокировку при прохождении поворотов. Основное применение типа 2 way — автоспорт.

По принципу действия, самоблокирующиеся дифференциалы можно подразделить на два основных типа: Speed sensitive – срабатывающих при возникновении разницы в угловых скоростях вращения полуосей. Torque sensitive – срабатывающих при падении усилия (крутящего момента) на одной из полуосей.

[править] SPEED SENSITIVE LSD

• Автоматическая блокировка с использованием Вискомуфты в качестве «Slip Limiter»

В данном случае применяется блокировка одной из полуосей с чашкой дифференциала.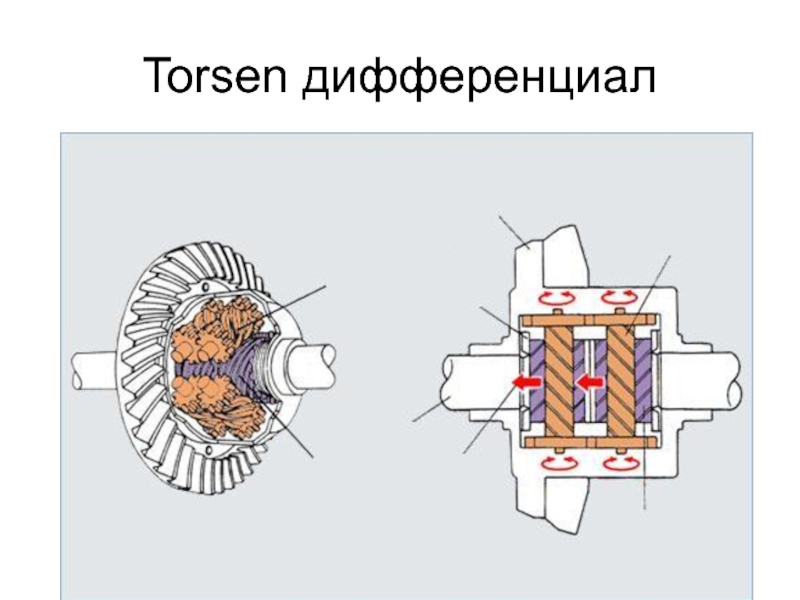 Вискомуфта монтируется соосно полуоси таким образом, что один её привод жестко крепится к чашке дифференциала, а другой – к полуоси.

При нормальном движении угловые скорости вращения чашки и полуоси одинаковые, либо незначительно отличаются (в повороте). Соответственно, рабочие плоскости вискомуфты имеют такое же небольшое расхождение в угловых скоростях и муфта остаётся разомкнутой. Как только одна из осей начинает получать более высокую угловую скорость вращения относительно другой, в вискомуфте появляется трение и она начинает блокироваться. Причем, чем больше разница в скоростях, тем сильнее трение внутри вискомуфты и степень её блокировки, а следовательно и степень блокировки дифференциала. За счет полученного момента трения между чашкой дифференциала и полуосью, дифференциал перераспределяет крутящий момент в пользу оси с наилучшим дорожным сцеплением (отстающую полуось).

По мере увеличения степени блокировки вискомуфты и выравнивания угловых скоростей чашки и полуоси, трение внутри вискомуфты начинает падать, что ведёт к плавному размыканию вискомуфты и к отключению блокировки.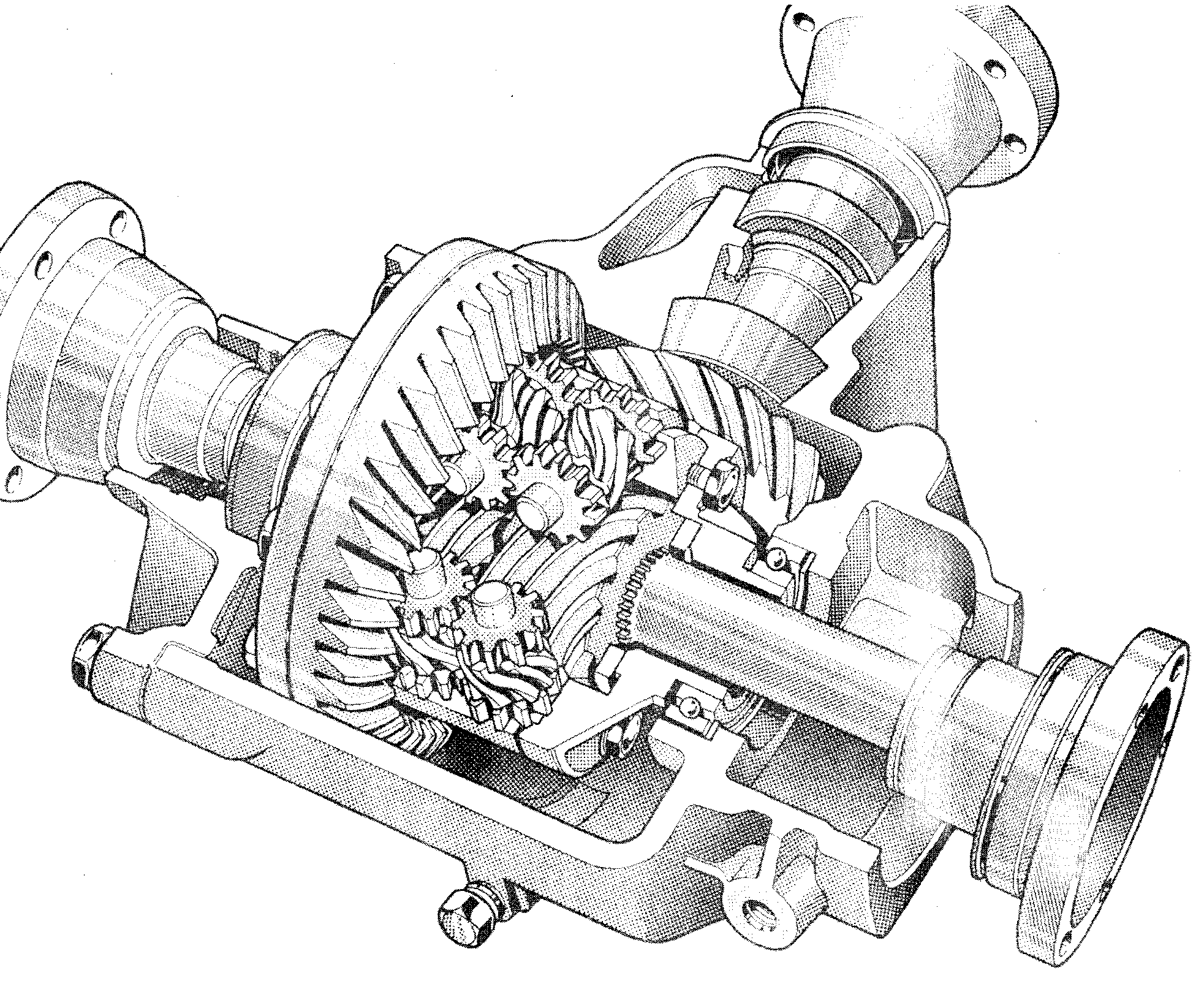

Данная схема применяется для межосевых дифференциалов, так как её конструкция слишком массивна для установки на мостовой редуктор. (Схема на картинке) Подобный механизм блокировки хорошо подходит для эксплуатации в условиях плохого дорожного покрытия, однако, в условиях настоящего бездорожья его способности далеко не выдающиеся: вискомуфта не справляется с постоянными сменами состояний сцепления мостов с грунтом, запаздывает при включении, перегревается и выходит из строя. Данный тип блокировки межосевого дифференциала можно встретить как в качестве основного и единственного средства блокировки на «паркетных» внедорожниках: Toyota Rav4, Lexus RX300 и.т.п., так и в качестве дополнительной блокировки (в дополнение к 100%-ой принудительной блокировке) на полноразмерных внедорожниках Toyota Land Cruiser

• Героторный дифференциал (Gerodisk или Hydra-lock)

Американская компания ASHA Corp. снабдила классический дифференциал устройством блокировки, состоящим из масленого насоса с поршнем и комплекта фрикционных пластин (фрикционного блока), установленного между чашкой дифференциала и шестерней одной из полуосей. Принцип действия данной блокировки практически ни чем не отличается от рассмотренной выше блокировки при помощи вискомуфты.

Масляный насос монтируется соосно полуоси таким образом, что его корпус крепится к чашке дифференциала, а нагнетающий ротор – к полуоси. При возникновении разности в угловых скоростях полуоси и чашки дифференциала, насос начинает нагнетать масло на поршень и сдавливать фрикционный блок, блокируя тем самым шестерню полуоси с чашкой дифференциала. За счет полученного момента трения, дифференциал перераспределяет крутящий момент на отстающую полуось (полуось с наилучшим сцеплением).

Данная конструкция получила название Gerodisk (Hydra-Lock) и штатно устанавливается на внедорожники Chrysler. Детальную компоновку устройства можно увидеть, кликнув на картинку. Практически для всех friction based дифференциалов необходимо применять специальное масло, которое содержит присадки, обеспечивающие нормальную работу фрикционных блоков.

[править] TORQUE SENSITIVE LSD

• Дифференциалы с фрикционными блоками предварительного натяга

Устройство таких дифференциалов довольно простое и принципиально ни чем не отличается от устройства обычного открытого дифференциала. Для создания дополнительного трения, между полуосями и чашкой дифференциала добавлены комплекты блоков фрикционных пластин (которые помечены на картинке справа красными точками). Именно поэтому, подобные дифференциалы часто именуют «friction based LSD». Довольно часто, фрикционные блоки подпружинивают. Когда начинается забегание одной из полуосей (буксование колеса), дифференциал перераспределяет крутящий момент в пользу отстающей полуоси за счет момента трения на фрикционных пластинах. Данный тип блокировки имеет очень большой недостаток – под действием трения пластин дифференциал препятствует возникновению даже небольшой разницы в угловых скоростях полуосей (которая необходима в поворотах), что негативно влияет на управляемость автомобиля, а так же на расход покрышек и топлива. В связи с этим, коэффициент блокировки данных дифференциалов обычно выбирают небольшим (иначе, автомобиль будет иметь неадекватную управляемость на дороге).

Тем не менее, для автоспорта выпускаются модели таких дифференциалов с довольно высоким конструктивно заложенным трением пластин и соответственно высоким коэффициентом блокировки. Помимо вышеперечисленных недостатков, можно выделить еще один – срок службы фрикционных блоков в таких дифференциалах небольшой и со временем, фрикционные блоки изнашиваются, снижая тем самым коэффициент блокировки дифференциала. Для всех friction based дифференциалов необходимо применять специальное масло, которое содержит присадки, обеспечивающие нормальную работу фрикционных блоков. Данные дифференциалы штатно устанавливаются в задний мост многих внедорожников — Toyota 4Runner (Hilux Surf), Toyota Land Cruiser, Nissan Terrano, Kia Sportage и.т.п.

• Самоблокирующиеся дифференциалы с гипоидным (червячным или винтовым) и косозубым зацеплением

Это одна из самых интересных, эффективных, технологичных и практически применяемых форм блокировки дифференциалов. Принцип работы основан на свойстве гипоидной или косозубой пары «расклиниваться» . В связи с этим, основные (или все) зацепления в таких дифференциалах косозубые или гипоидные. Разновидностей конструкций не так уж и много — можно выделить три основных типа.

Первый тип производит компания Zexel Torsen [1]. (T-1) Гипоидными парами являются шестерни ведущих полуосей и сателлиты. При этом каждая полуось имеет собственные сателлиты, которые парно связанны с сателлитами противоположной полуоси обычным прямозубым зацеплением. Следует отметить, что ось сателлита перпендикулярна полуоси. При нормальном движении и равенстве передаваемых на полуоси крутящих моментов, гипоидные пары «сателлит / ведущая шестерня» либо остановлены, либо проворачиваются, обеспечивая разницу угловых скоростей полуосей в повороте. Как только одна из полуосей начинает буксовать и крутящий момент на ней падает, гипоидные пары «полуось/сателлит» начинают вращаться и расклиниваться, создавая трение с чашкой дифференциала и друг с другом, что приводит к частичной блокировке дифференциала. За счет момента трения, дифференциал перераспределяет крутящий момент в пользу отстающей полуоси. Данная конструкция работает в самом большом диапазоне распределения крутящего момента — от 2. 5/1 до 5.0/1. Диапазон срабатывания регулируется углом наклона зубцов червяка.

Автором второго типа является англичанин Rod Quaife[2]. В данном дифференциале используются косозубые шестерни полуосей и винтовые шестерни сателлитов. Оси сателлитов параллельны полуосям. Сателлиты расположены в своеобразных карманах чашки дифференциала. При этом парные сателлиты имеют не прямозубое зацепление, а образуют между собой еще одну гипоидную пару, которая расклиниваясь, так же участвует в процессе блокировки (на картинке слева). Подобное устройство имеет и дифференциал True Trac компании Tractech[3]. Даже у нас в России появилось производство аналогичных дифференциалов под отечественные автомобили УАЗ и.т.д. А вот компания Zexel Torsen[4] в своём дифференциале T-2 предложила немного другую компоновку по сути, того же устройства (на картинке справа). Благодаря своей необычной конструкции, парные сателлиты соединены между собой со внешней стороны солнечных шестерней. По сравнению с первым типом, эти дифференциалы имеют меньший коэффициент блокировки, однако они более чувствительны к разнице передаваемого момента и срабатывают раньше (начиная от 1.4/1). Компания Tractech недавно выпустила мостовой torque sensitive дифференциал Electrac, снабженный принудительной электроприводной блокировкой.

Третий тип производится компанией Zexel Torsen (Т-3) и используется в основном для межосевых дифференциалов. Как и во втором типе, в данном дифференциале используются косозубые шестерни полуосей и винтовые шестерни сателлитов. Оси сателлитов параллельны полуосям. Планетарная структура конструкции позволяет сместить номинальное распределение крутящего момента в пользу одной из осей. Например, используемый на 4Раннере 4-го поколения дифференциал Т-3 имеет номинальное распределение момента 40/60 в пользу задней оси. Соответственно, смещен и весь диапазон работы частичной блокировки: от (front/rear) 53/47 до 29/71. В целом, смещение номинального распределения момента между осями возможно в диапазоне от 65/35 до 35/65. Срабатывание частичной блокировки обеспечивает 20-30% перераспределение передаваемых на полуоси моментов. Так же, подобная структура дифференциала делает его компактным, что в свою очередь, упрощает конструкцию и улучшает компоновку раздаточной коробки.

Вышеописанные дифференциалы очень популярны в автоспорте. Более того, многие производители устанавливают такие дифференциалы на свои модели штатно, как в качестве межосевых, так и межколёсных дифференциалов. Например, Тойота устанавливает такие дифференциалы как на легковые автомобили (Supra, Celica, Rav4, Lexus IS300, RX300 и.т.д), так и на внедорожники (4Runner (Hilux Surf), Land-Cruiser, Mega-Cruiser, Lexus GX470) и автобусы (Coaster Mini-Bus). Данные дифференциалы не требуют применения специальных присадок к маслу (в отличии от friction-based дифференциалов), однако лучше использовать качественное масло для нагруженных гипоидных передач.

Самоблокирующийся дифференциал — тип дифференциала с блокировкой, срабатывающей в случае появления большой разницы в скорости вращения полуосей привода колес. Существует несколько конструкций блокировок для разных дорожных покрытий и типов автомобилей.

Вместо введения

Прошлая статья о дифференциалахзакончилась на обещании рассказать о видах блокировок дифференциалах, и придётся снова пугать вас длительным техническим текстом. Поехали, как сказал Ю.А.Гагарин 58 лет назад.

О чём речь?

Итак, аббревиатура LSD, которая указана в названии статьи, является сокращением от Limited Slip Differential, а по-русски — дифференциал с повышенным внутренним сопротивлением. В прошлой статье мы рассказали вам о принципах работы свободного дифференциала, и тут мы уже не будем на этом останавливаться. В конструкции LSD предусмотрен момент блокировки, который допускает разницу скорости вращения валов, но срабатывать блокировка будет только в случае большой диспропорции.

Это про бездорожье, правда?

Процентов на 50%. Такие блокировки применяются и во внедорожниках, и в спорткарах. Первый случай — автомобиль не должен застрять. Второй случай — необходим ровный старт, без проскальзывания на асфальте.

Как работает LSD?

Такая блокировка вне зависимости от конструкции будет работать только после момента, в который разница угловых скоростей колёс превышает определённый лимит. После этого срабатывает блокировка, и крутящий момент распределяется в равных частях на оба колеса. Продолжаться это будет либо до восстановления контакта с дорогой, либо до полной потери сцепления. Это вы можете выбрать самостоятельно.

А я слышал про Вискомуфты. Что это такое?

Хороший вопрос. Ведущие мосты в легковых автомобилях обычно имеют в своём запасе два варианта блокировок. Первый тип основан на чувствительности к разнице скоростей, а второй тип блокировки чувствителен к разнице в передаче крутящего момента. Современные автомобили в подавляющем большинстве наслаждаются блокировками первого типа. Именно в этом месте появляется слово «вискомуфта». Вискомуфта представляет собой пакет круглых плоских фрикционных дисков, установленных внутри герметичного корпуса. В пакете есть диски двух типов, соединенные с ведущим и ведомым валами соответственно. На поверхности дисков есть отверстия и небольшие выступы. Пакет дисков собран так, чтобы ведомые и ведущие диски чередовались между собой и находились на малом расстоянии. Внутренняя полость муфты заполнена силиконовым гелем.

Такая муфта проста в производстве и неприхотлива в обслуживании. Второй тип механических блокировок дороже и может сломаться раньше.

Хорошие и разные LSD

Дифференциалы такого типа различаются по своим типам. Про них мы вам расскажем ниже.

Вязкостные дифференциалы

Этот распространённый тип дифференциала основан на действии вискомуфты.

Такие дифференциалы заслужили популярность из-за плавности своей работы. Принцип действия у них основан на изменениях свойств специального геля, которые меняются бесступенчато. Такое свойство удовлетворяет желанию производителей повысить комфорт для водителя.

Конечно, вязкостные здания имеют свои недостатки.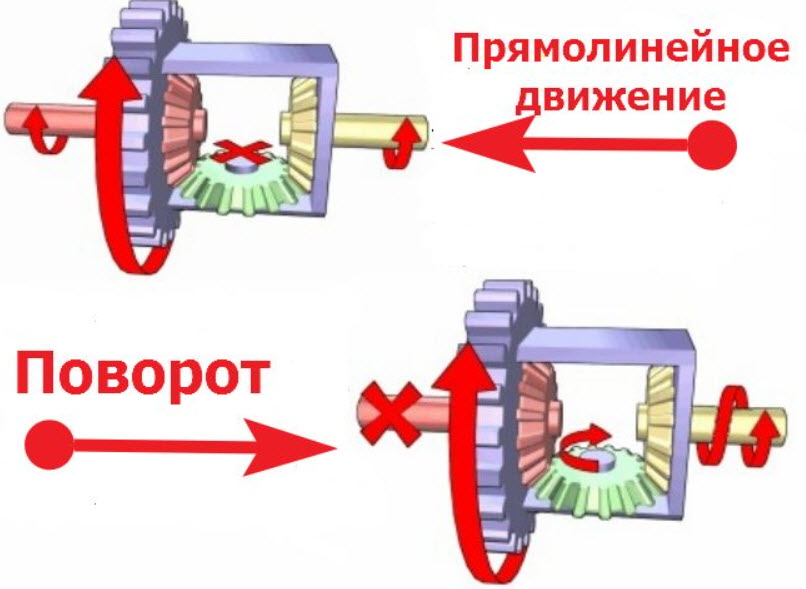 Любой узел, который работает за счёт давления жидкости, теряет часть энергии при работе, что вызывает увеличение расхода топлива. Также они крайне чувствительны к перегревам и просто повышенным нагрузкам. Вискогель теряет рабочие свойства при повышении температур. Соответственно? если вы побуксовали в снегу продолжительное время — работа блокировки в следующий раз может быть и хуже. Механические блокировки в этом же случае работают одинаково, вплоть до поломки.

Такие дифференциалы могут требовать замены каждые 100 тысяч километров.

Такие системы очень чувствительны к состоянию уплотнений в системе, ведь внутренняя часть дифференциала полностью герметична. Если произошла разгерметизация — вискомуфту меняют.

Героторный насос

В этих дифференциалах с внутренней стороны установлен героторный насос, а на вращающемcя валу привода укрепили зубчатое колесо, которое находится внутри насоса. Если при вращении корпуса героторного насоса и зубчатого колеса появляется разница в скорости — жидкость сжимается. После этого крутящий момент уходит на «отстающее» колесо, которое имеет сцепление с дорогой. Эти системы стремительно набирают популярность по мере увеличения степени компьютерного управления узлами автомобиля (системы EBD и тому подобные), так как, в отличие от вискомуфты, работой героторного насоса можно управлять.

Про крутящий момент

К этому типу относятся механически дифференциалы червячного типа, обеспечивающие автоматическую блокировку при возникновении разности крутящих моментов между корпусом и приводным валом. Если одно из колес проскальзывает, крутящий момент падает, червячный дифференциал перераспределяет крутящий момент на свободное колесо. При этом колесо блокируется не полностью, и степень блокировки зависит от степени падения крутящего момента. Самоблокирующиеся дифференциалы типа «Торсен» Слово Torsen в наше время — торговая марка, а образовалось оно при сложении двух слов «torque» — «крутящий момент» и «sensing» — «чувствительный». Под маркой Torsen выпускаются конструкции двух типов. Самоблокирующиеся дифференциалы типа «Квайф»

Вместо послесловия

Данный текст предназначен для понимания вами механики работы того самого узла, который помогает вам выехать из сугроба в тот самый день, когда коммунальщики забыли поработать. Ну или вы очень хотите прокатиться по полю на дачу. Думаю, на этом можно заканчивать цикл статей про этот узел, и готовить вам очередную техническую информацию про другие узлы автомобиля, которыми вы пользуетесь каждый день, но даже не подозреваете, как они работают.

Английскую аббревиатуру LSD (limited slip differential) на русский язык можно перевести как дифференциал с повышенным внутренним сопротивлением. Стандартный (открытый, свободный) дифференциал допускает наличие разницы в угловых скоростях выходных валов, вплоть до полной остановки одного из них. Это можно наблюдать на застрявшей в грязи машине, когда одно колесо прокручивается, а другое стоит на месте. В конструкции дифференциала LSD предусмотрена блокировка, допускающая небольшую разницу в скорости вращения валов, но срабатывающая в случае большой диспропорции между ними. В автомобилях такие дифференциалы с блокировкой используются в двух основных случаях: если это внедорожник, или если это — спортивный автомобиль с двигателем, обеспечивающим чрезмерный крутящий момент. В первом случае блокировка срабатывает, чтобы автомобиль не застревал, а во втором — для обеспечения эффективного старта с места, чтобы колеса не проскальзывали на асфальте.

Принцип работы дифференциала LSD

Блокировка, вне зависимости от конструкции, срабатывает, когда разницы в угловых скоростях колёс превышает определенный, заранее установленный предел. После срабатывания блокировки крутящий момент передаётся на оба колеса в равной пропорции. Это продолжается либо до восстановления контакта с дорогой обоими колесами, либо до полной потери сцепления с поверхностью.

Популярные виды LSD-дифференциалов

В конуструкции блокировок, использующихся в ведущих мостах легковых автомобилях, преобладают два основных типа.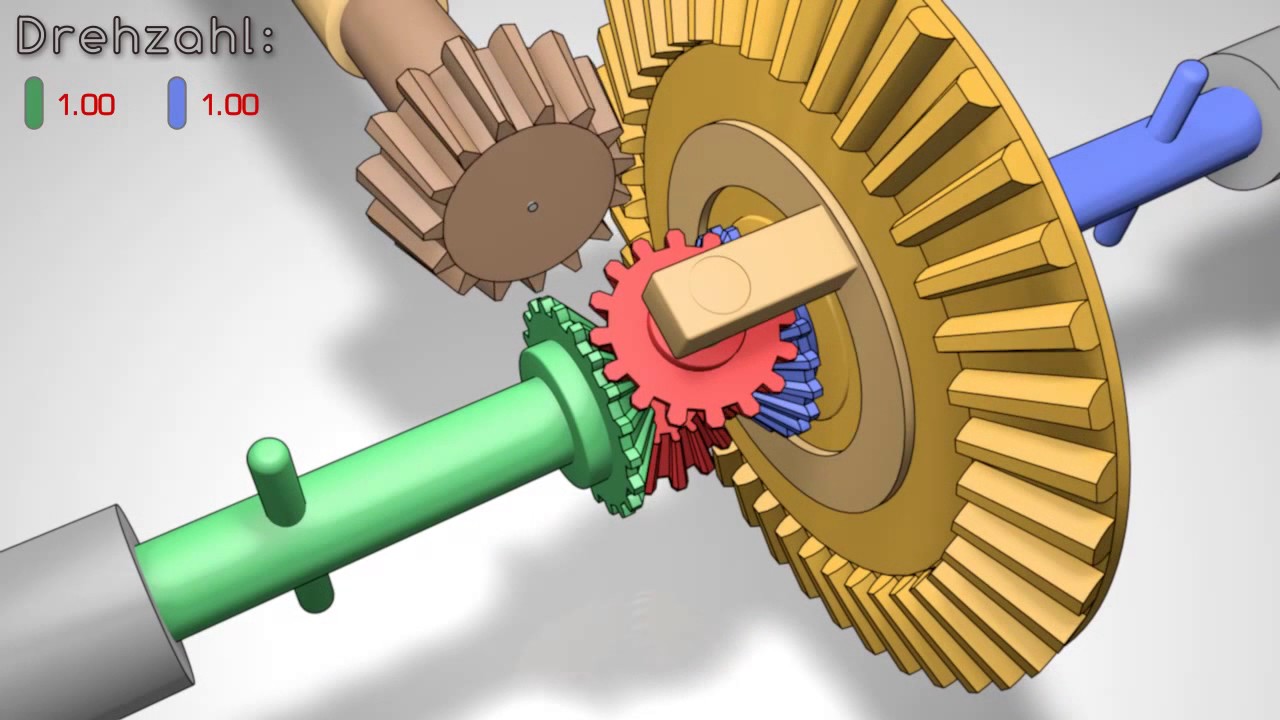 Конструкция первого типа основана на чувствительности к разнице скоростей. Второй тип конструкции — механизм, чувствительный к появлению разницы в передаче крутящего момента. В современных автомобилей чаще встречаются блокировки первого типа становятся всё более популярными. Причина в том, что к первому типу относятся блокировки на основе вискомуфты, то есть простые в производстве и неприхотливые в обслуживании. Относящиеся ко второму типу механические блокировки дороже и раньше выходят из строя за счет применения большого количества деталей.

Дифференциалы LSD, чувствительные к разнице скоростей

Распространенный тип дифференциала повышенного трения, основанный на действии вискомуфты. Помимо надежности заслужили популярность плавностью работы — их действие основано на изменениях в свойствах специального геля, меняющихся бесступенчато. Поскольку основная тенденция в развитии современных автомобилей — стремление любыми способами повысить комфорт для водителя, это свойство оказалось ценным. Однако у вязкостных дифференциалов есть и свои недостатки. Как и в любом узле, в котором передача усилия производится за счет давления жидкости, при их работе теряется часть энергии, что приводит к повышению расхода топлива. Во-вторых, они крайне чувствительны к повышенным нагрузкам — перегрев отрицательно действует на гель, лишая его рабочих свойств. Иными словами, побуксовав в снегу в течение продолжительного времени, можно быть уверенным, что работа блокировки ухудшилась и в следующий раз будет уже менее эффективной. Механические блокировки, например, работают одинаково вплоть до поломки. В общем случае вязкостный дифференциал требует замены при пробеге 100 тысяч километров.

Как и любой другой резервуар с жидкостью, вискомуфта чувствительна к состоянию уплотнений. Поэтому внутреннюю часть дифференциала делают полностью герметичной, чтобы силиконовый гель не смешивался с трансмиссионным маслом, смазывающим шестерни. В случае разгерметизации вискомуфту извлекают и заменяют новой.

Дифференциалы на основе героторного насоса

В дифференциалах этого типа с внутренней стороны установлен вращающийся героторный насос, а на вращающемся приводном валу укреплено зубчатое колесо, которое находится внутри насоса. При возникновении разницы в в скорости вращения корпуса героторного насоса и зубчатого колеса, происходит сжатие жидкости внутри насоса. Находящаяся под давлением жидкость передает крутящий момент на «отстающее» колесо, которое в данный момент стремится остановиться, так как имеет сцепление с дорогой. Эти системы стремительно набирают популярность по мере увеличения степени компьютерного управления узлами автомобиля (системы EBD и тому подобные), так как, в отличие от вискомуфты, работой героторного насоса можно управлять.

Дифференциалы LSD, чувствительные к разнице в передаче крутящего момента

К этому типу относятся механически дифференциалы червячного типа, обеспечивающие автоматическую блокировку при возникновении разности крутящих моментов между корпусом и приводным валом. Если одно из колес проскальзывает, крутящий момент, падает, червячный дифференциал перераспределяет крутящий момент на свободное колесо. При этом колесо блокируется не полностью, и степень блокировки зависит от степени падения крутящего момента. Самоблокирующиеся дифференциалы типа «Торсен»

Слово Torsen в наше время — торговая марка, а образовалось оно при сложении двух слов «torque» — «крутящий момент» и «sensing» — «чувствительный». Под маркой Torsen выпускаются конструкции двух типов. Самоблокирующиеся дифференциалы типа «Квайф»

Сателлиты дифференциала типа Quaife (их обычно 10) не крепятся на осях, как у аналогов, а находятся в закрытых нишах корпуса. Все они параллельны полуосям, однако в отличие от Torsen Т-2, где каждый сателлит постоянно контактирует с обеими полуосевыми шестернями, в Quaife правый ряд сателлитов находится в контакте с правой полуосевой шестерней, левый – с левой.

Математика онлайн

Решение математики онлайн

Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.

Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.

Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.

О калькуляторах

По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.

Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]

Преимущества

1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.

2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.

3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.

4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.

5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.

Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.

Межосевой дифференциал

Что такое межосевой дифференциал?

Как правило, секрет выносливости внедорожников заключается в их особой конструкции, в основе которой задействована рама повышенной жесткости, мощном двигателе, а также присутствии системы полного привода и раздаточной коробки, осуществляющей распределение крутящего момента на автомобильные оси, и, в случае необходимости, увеличивающей его до нужного значения. В свою очередь, «раздатка» нового поколения состоит из таких элементов, как межосевой дифференциал, передача цепного типа, служащая для передачи крутящего момента двигателя на переднюю ось авто, и понижающая передача.

При этом именно присутствие межосевого дифференциала можно назвать главной отличительной особенностью строения раздаточной коробки, являющейся неотъемлемой частью полноприводной системы. Данный элемент необходим для обеспечения возможности вращения ведущих осей автомобиля с разными скоростями. А, для полной реализации возможностей системы, в ней существует такая функция, как блокировка межосевого дифференциала, представляющая собой самый эффективный способ улучшения проходимости автомобиля.

Реализация данной функции может осуществляться автоматически и вручную. Во втором случае блокировка производится самим водителем. Происходит это при помощи специального устройства – привода, который может быть механическим, гидравлическим, электрическим или пневматическим. Данный тип блокировки носит название принудительного.

Принудительная блокировка межосевого дифференциала подразумевает фактически полное прекращение выполнения своих функций и трансформирмацию в обычную муфту, осуществляющую жесткую сцепку полуосей или карданов авто и передающую им одинаковую величину крутящего момента с одинаковой угловой скоростью. Применяется для преодоления машиной труднопроходимых участков, а при их прохождении обязательно выключается.

Автоматическая блокировка, иначе именуемая блокировкой дифференциалов с частичным проскальзыванием, производится при помощи таких конструкций, как:

• Вискомуфта,
• Дифференциал Torsen,
• Фрикционная муфта.

Вискомуфта, ее строение и механизм действия

Крепление вискомуфты производится одним приводом к чашке дифференциала, в то время как второй его конец прикрепляется к полуоси авто. Когда автомобиль находится в обычном режиме движения, чашка и полуось вращаются с одинаковыми угловыми скоростями. Данные показатели могут лишь незначительно отличаться между собой при прохождении поворотов. То есть и сами рабочие плоскости вискомуфты в это время имеют минимальный процент расхождения, и сама она находится в раскрытом виде. Если же на какую-либо из осей автомобиля передается большее значение крутящего момента, в результате чего скорость ее вращения значительно превышает аналогичный показатель других осей, в вискомуфте возникает трение, из-за чего происходит ее блокировка.

Получается, что, чем больше отличаются друг от друга угловые скорости вращения осей авто, тем больше трения возникает в вискомуфте и тем сильнее становится степень ее блокировки. В свою очередь, после их выравнивания, трение постепенно снижается, что приводит к плавному размыканию вискомуфты и отключению блокировки.

Данный межосевой блокируемый дифференциал наиболее хорошо показывает себя при использовании автомобиля на покрытии низкого качества, однако в условиях настоящего бездорожья он показывает себя не самым лучшим способом. Дело в том, что вискомуфта просто не в состоянии справиться с быстрыми и частыми сменами состояния сцепления мостов авто с грунтом, из-за чего она перегревается и выходит из строя.

Особенности устройства дифференциала Torsen и его типы

В свою очередь, самоблокирующийся дифференциал Torsen представляет собой одну из самых высокотехнологичных и эффективных форм блокировки. Он отличается лучшей реакцией и способностью в минимально короткое время «откликаться» на изменения величины крутящего момента, отвечая на это изменением степени блокировки. Именно внедорожники с межосевым дифференциалом данного типа блокировки являются наиболее надежными. В основе его действия используются свойства гипоидной или косозубой пары зацеплений, которые, при необходимости, могут «расклиниваться». Конструкция данного типа имеет три разновидности:

Тип 1

В качестве гипоидных пар здесь задействованы шестерни и сателлиты ведущих полуосей. Сателлиты противоположных полуосей, расположенные по отношению к ним в перпендикулярном положении, связываются между собой зацеплениями прямозубого типа.

При обычном режиме движения, когда крутящие моменты распределяются на оси авто в одинаковой степени, эти пары находятся в стационарном положении либо двигаются с небольшой интенсивностью, обеспечивая оптимальную разницу угловых скоростей осей при прохождении поворотов. В случаях, когда отмечается «пробуксовка» одной из осей, что выражается в падении на ней крутящего момента, пары «сателлит-полуось» начинают вращательные движения, что приводит к возникновению трения и частичной блокировке дифференциала. В свою очередь, в этот же момент происходит распределение крутящего момента в пользу менее интенсивно работающей полуоси.

Стоит отметить, что дифференциал Torsen  1го типа имеет самкю мощную конструкцию в классе, так как работает в самом широком диапазоне отношений крутящего момента — от 2.5/1 до 5.0/1.

Тип 2

В основе конструкции данного дифференциала, созданного английским конструктором Родом Квайфом, используются шестерни полуосей косозубого типа и винтовые шестерни сателлитов, расположенных параллельно полуосям. Если сравнивать их с предыдущим типом, можно заметить, что схема межосевого дифференциала данного типа отличается меньшим коэффициентом блокировки, компенсирующимся более высокой скоростью срабатывания и большей чувствительностью к изменениям передаваемого крутящего момента. Подобные механизмы используются на автомобилях отечественного производства, включая УАЗы.

Тип 3

Устройство межосевого дифференциала Torsen третьего типа от компании Zexel Torsen по своим конструктивным особенностям и принципу действия во многом схоже со вторым типом. Здесь также задействованы шестерни полуосей косозубого типа и винтовые шестерни сателлитов, оси которых находятся в параллельном положении по отношению к полуосям.

Благодаря планетарной структуре строения данной конструкции обеспечивается смещение номинального распределения крутящего момента в пользу той или другой оси авто. Главным же достоинством данного типа блокирующего устройства является его функциональность и компактность, что дает возможность для упрощения конструкции раздаточной коробки и уменьшения ее размеров.

Конструкционные отличия фрикционных муфт

В конструкцию фрикционной муфты входит барабан, который имеет непосредственную связь со ступицей авто, несколько фрикционных дисков трения (два и более), поршень, осуществляющий сжатие этих дисков и пружину, возвращающую поршень в исходное положение.

Между барабаном и ступицей существует жесткая связь. При этом внутри последней располагается кольцо, выполняющее функцию стопора, на котором находится тарельчатая пружина, опирающаяся на поршень. В свою очередь, ступица оборудуется специальными каналами, осуществляющими передвижение масла между поршнем и барабаном. В автомобилях легкового типа чаще всего используются дисковые фрикционные муфты, имеющие две поверхности трения, состоящие из одного диска и двух полумуфт, а многодисковую конструкцию чаще можно встретить на специализированном транспорте, в том числе, на тракторах.

Рассмотрим, как работает межосевой дифференциал с фрикционной муфтой: в момент нахождения автомобиля в обычном, плавном режиме движения, распределение угловых скоростей между осями авто происходит равномерно. Однако когда какая-либо из полуосей начинает вращаться быстрее, фрикционные диски начинают сближаться между собой, притормаживая ее при помощи возникающих сил трения.

Подобная система блокировки отличается хорошей эффективностью, однако на серийных легковых автомобилях ее можно увидеть достаточно редко. Данная тенденция объясняется сложностью конструкции и особой спецификой обслуживания фрикционных дифференциалов, а также небольшим ресурсом работоспособности, вызванным быстрым износом их составляющих.

Принцип работы межосевого дифференциала фрикционного типа применяется в муфте Haldex, выпуск которой, начиная с 1998 года, осуществляет шведская фирма с одноименным названием. В основе действия данного устройства производители использовали работу электрогидравлической связки элементов. Но, несмотря на прогрессивность и инновационный дух муфты Haldex, первые ее версии были скорее провальными, чем успешными, что вызвало необходимость проведения многочисленных доработок конструкции, причем последние разработки оказались, весьма удачными и востребованными.

На данный момент осуществляется выпуск 5-го поколения муфты Haldex, отличающейся улучшенными характеристиками, включающими:

• возможность управления устройством вне зависимости от режима движения;
• способность быстрого увеличения крутящего момента с использованием упреждающего управления;
• возможность постоянной работы задней главной передачи;
• совместимость с различными системами управления тормозами авто, включая ABS.

Заключение

Проанализировав данную информацию, можно понять, зачем нужен межосевой дифференциал. Говоря простым языком, его можно назвать распределителем вращательного момента на колеса авто, функционирующим по принципу аптечных весов: если на оба плеча механизма оказывается одинаковая нагрузка, то при «поднятии за хвост» они поднимаются одинаково, если же на одно из них оказывается большая нагрузка – второе плечо будет подниматься для сохранения равновесия.

Дифференциал функции

Определение дифференциала функции

Рассмотрим функцию \(y = f\left( x \right),\), которая непрерывна в интервале \(\left[ {a,b} \right].\) Предположим, что в некоторой точке \({x_0 } \in \left[ {a,b} \right]\) независимая переменная увеличивается на \(\Delta x.\) Приращение функции \(\Delta y\), соответствующее изменению независимой переменной \(\Delta x\) равно

\[\Delta y = \Delta f\left( {{x_0}} \right) = f\left( {{x_0} + \Delta x} \right) — f\left( {{x_0}} \right ).\]

Для любой дифференцируемой функции приращение \(\Delta y\) можно представить в виде суммы двух членов:

\[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right),\]

, где первый член (называемый главной частью приращения) линейно зависит от приращения \(\Delta x,\), а второй член имеет более высокий порядок малости по отношению к \(\Delta x.\) выражение \(A\Delta x\) называется дифференциалом функции и обозначается \(dy\) или \(df\left( {{x_0}} \right).2.\)

Обратите внимание, что в этом примере коэффициент \(A\) равен значению производной от \(S\) в точке \({x_0}:\)

\[А = 2{х_0}.\]

Оказывается, для любой дифференцируемой функции справедлива следующая теорема:

Коэффициент \(A\) при главной части приращения функции в точке \({x_0}\) равен значению производной \(f’\left( {{x_0}} \right )\) в этот момент, то есть приращение \(\Delta y\) равно

\[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right) = f’\left({{x_0}} \right)\Delta x + \omicron\left( {\ Дельта х} \справа).\]

Деление обеих частей уравнения на \(\Delta x \ne 0\) дает

\[\frac{{\Delta y}}{{\Delta x}} = A + \frac{{\omicron\left({\Delta x} \right)}}{{\Delta x}} = f ‘\left( {{x_0}} \right) + \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}}.\]

В пределе как \(\Delta x \to 0\) мы получаем значение производной в точке \({x_0}:\)

\[y’\left( {{x_0}} \right) = \lim\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = A = f’ \влево( {{x_0}} \вправо).\]

Здесь мы учли, что для малой величины \(\omicron\left( {\Delta x} \right)\) более высокого порядка малости, чем \(\Delta x,\) предел равен

\[\lim\limits_{\Delta x \to 0} \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}} = 0.\]

Предполагая, что дифференциал независимой переменной \(dx\) равен ее приращению \(\Delta x:\)

\[дх = \Дельта х,\]

получаем из отношения

\[dy = A\Delta x = y’dx\]

то

\[y’ = \frac{{dy}}{{dx}},\]

я.т. е. производную функции можно представить как отношение двух дифференциалов.

Геометрический смысл дифференциала функции

На рис. \(2\) схематично показано разбиение приращения \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член более высокого порядка малости \(\ омикрон\влево({\Delta x}\вправо).\)

Рис. 2.

Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M,\), как известно, имеет угол наклона \(\alpha,\) тангенс которой равен производной:

\[\tan \alpha = f’\left( {{x_0}} \right).\]

Когда независимая переменная изменяется на \(\Delta x\), тангенс увеличивается на \(A\Delta x.\) Это линейное приращение, образованное тангенсом, является просто дифференциалом функции. Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\)

Свойства дифференциала

Пусть \(и\) и \(v\) — функции переменной \(х\).Дифференциал имеет следующие свойства:

1. Постоянная может быть вынесена за знак дифференциала:

   \[d\влево( {Cu} \вправо) = Cdu,\]

   где \(С\) — постоянное число.
2. Дифференциал суммы (разности) двух функций равен сумме (разности) их дифференциалов:

   \[d\left( {u \pm v} \right) = du \pm dv.\]

3. Дифференциал константы равен нулю:

   \[d\влево(С\вправо) = 0.\]

4. Дифференциал независимой переменной \(x\) равен ее приращению:

   \[dx = \Delta x.{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\]

   и так далее.

   Формоинвариантность дифференциала

   Рассмотрим композицию двух функций \(y = f\left( u \right)\) и \(u = g\left( x \right).\). Ее производную можно найти по цепному правилу:

   \[{y’_x} = {y’_u} \cdot {u’_x},\]

   , где субиндекс обозначает переменную дифференцирования.

   Дифференциал «внешней» функции \(y = f\left( u \right)\) можно записать как

   \[dy = {y’_u}\,du. 2}}} = — \ frac {\ pi }{ 2}.2}дх.\]

   Дополнительные проблемы см. на стр. 2.

   Дифференциалы

   Производную функции часто можно использовать для аппроксимации определенных значений функции с удивительной степенью точности. Для этого необходимо ввести понятие дифференциала независимой переменной и зависимой переменной.

   Определение производной функции y = f(x) , как вы помните, равно

    

   , который представляет наклон касательной к кривой в некоторой точке ( x, f(x) ).Если Δ x очень мало (Δ x ≠ 0), то наклон касательной примерно такой же, как наклон секущей через ( x, f(x) ). То есть

    

   Дифференциал независимой переменной x записывается как dx и совпадает с изменением x , Δ x . То есть

    

   Дифференциал зависимой переменной y , записанный как dy , определяется как

    

   Из предыдущего обсуждения можно сделать вывод, что дифференциал y(dy ) примерно равен точному изменению y (Δ y ) при условии, что изменение x (Δ x = dx ) относительно мала.Чем меньше изменение x , тем ближе dy будет к Δ y , что позволит вам аппроксимировать значения функции, близкие к f(x) (рис. ) .

   Рисунок 1 Аппроксимация функции с помощью дифференциалов.

   Пример 1: Найдите dy для y = x ³ + 5 x −1.

    

   Пример 2: Используйте дифференциалы, чтобы приблизить изменение площади квадрата, если длина его стороны увеличивается с 6 см до 6.23 см.

   Пусть х = длина стороны квадрата. Площадь может быть выражена как функция x , где y = x ² . Дифференциал dy это

    

   Поскольку x увеличивается с 6 до 6,23, вы обнаружите, что Δ x = d x = 0,23 см; следовательно,

    

   Площадь квадрата увеличится примерно на 2,76 см ² по мере увеличения длины его стороны с 6 до 6.23. Обратите внимание, что точное увеличение площади (Δ y ) составляет 2,8129 см ² .

   Пример 3: Используйте дифференциалы для аппроксимации значения до ближайшей тысячной.

   Поскольку функция, которую вы применяете, имеет вид , выберите подходящее значение x , которое представляет собой идеальный куб и относительно близко к 26,55, а именно x = 27. Дифференциал dy равен

    

   Потому что x уменьшается с 27 до 26.55, вы обнаружите, что Δ x = dx = -0,45; следовательно,

    

   , что означает, что это будет примерно на 1/60 меньше, чем ; следовательно,

      

   с точностью до тысячной.

   Обратите внимание, что значение калькулятора равно 2,983239874, которое округляется до того же ответа до ближайшей тысячной!

   1. Дифференциал

   Ранее в главе о дифференцировании мы написали `dy/dx` и `f'(x)`, чтобы обозначить одно и то же. Мы использовали `d/dx` как оператор .

   Теперь мы видим другой способ записи и осмысления производной.

   Мы будем использовать эту новую форму производной на протяжении всей главы, посвященной интеграции.

   Определения

   Дифференциалы бесконечно малые величины. Обычно мы записываем дифференциалы как `dx,` `dy,` `dt` (и так далее), где:

   `dx` — бесконечно малое изменение `x`;

   `dy` — это бесконечно малое изменение `y`; и

   `dt` — это бесконечно малое изменение `t`.

   При сравнении небольших изменений величин, которые связаны друг с другом (например, в случае, когда `y` является некоторой функцией f `x`, мы говорим дифференциал `dy`, `y = f(x)` записывается:

   `dy = f'(x)dx`

   Примечание: Теперь мы рассматриваем `dy/dx` больше как дробь (где мы можем манипулировать частями по отдельности), а не как оператор .5-x.2−4x+2`, тогда f(x)=10x-4`.

   Таким образом, дифференциал определяется как:

   `dy = (10x-4)dx`

   Примечание

   Мы могли бы использовать дифференциал для оценки реальное изменение значения функции (`Δy`), вызванное небольшим изменение `x` (записывается как `Δx`). Много учебников сделать это, но это довольно глупо, так как мы можем легко найти точное изменение — зачем приближать его?

   Мы вводим здесь дифференциалы как введение в нотация, используемая в интеграции .

   Как dy, dx и Δ у и Δ x связаны?

   `Дельта y` означает «изменение `y`, а `Дельта x` означает «изменение `x`».

   Ранее в главе «Дифференциация» мы узнали, что наклон кривой в точке P определяется как «dy/dx».

   Наклон пунктирной линии определяется отношением `(Delta y)/(Delta x).` По мере того, как `Delta x` становится меньше, этот наклон становится ближе к фактическому наклону P , что является «мгновенным» отношением `dy/dx`.

   То есть

   `lim_(Дельта x->0) (Дельта y)/(Дельта x)=dy/dx`

   См. «Наклон касательной», чтобы узнать об этом.

   Теперь мы переходим к изучению того, как дифференциал используется для выполнения противоположного процесса дифференциации, который сначала мы назовем антидифференцировкой , а затем интеграцией .

   Деловой расчет

   Дифференциальное уравнение — это уравнение, включающее производную функции. Они позволяют нам выразить простым уравнением связь между величиной и скоростью ее изменения.

   Пример 1

   Банк выплачивает 2% годовых по своим депозитным сертификатам, но взимает ежегодную комиссию в размере 20 долларов. Напишите уравнение для скорости изменения баланса \( B'(t) \).

   Если баланс \( B(t) \) выражен в долларах, то \( B'(t) \) выражен в долларах в год.Когда мы думаем о том, что меняет баланс счета, есть два фактора:

   1. Проценты, увеличивающие остаток, и
   2. Комиссия, уменьшающая баланс.

   Учитывая проценты, мы знаем, что каждый год баланс будет увеличиваться на 2%, но 2% чего? Каждый год это будет меняться, поскольку мы зарабатываем проценты на любом текущем балансе. Мы можем представить сумму увеличения как 2% от баланса: \(0,02B(t)\) долларов/год.

   Плата уже указана в долларах/год. Поскольку все теперь имеет одинаковые единицы измерения, мы можем сложить их вместе и составить уравнение: \[ B'(t)=0,02B(t)-20. \]

   Результат представляет собой пример дифференциального уравнения. Обратите внимание, что это конкретное уравнение включает в себя как производную , так и исходную функцию, поэтому мы не можем просто найти \( B(t) \) с помощью базового интегрирования.

   Алгебраические уравнения содержат константы и переменные, а решениями алгебраического уравнения обычно являются числа.3 — 4\).

   Вы уже решили множество дифференциальных уравнений: каждый раз, когда вы находили первообразную функции \(f(x)\), вы решали дифференциальное уравнение \(y’ = f(x)\), чтобы получить решение \( у\). Однако дифференциальное уравнение \(y’ = f(x)\) — это только начало. Другие приложения генерируют другие дифференциальные уравнения, как в приведенном выше примере банковского баланса.

   Проверка решений дифференциальных уравнений

   Независимо от того, легко или трудно решить дифференциальное уравнение, важно иметь возможность проверить, действительно ли возможное решение удовлетворяет дифференциальному уравнению.2} = 2, \] результат, который мы хотели проверить.

Разделимые дифференциальные уравнения

Дифференциальное уравнение называется разделимым, если переменные можно разделить алгебраически так, что все \(х\) и \(дх\) являются одной частью уравнения, а все \(у\) и \(dy\) находятся на другой стороне уравнения. Другими словами, уравнение имеет вид \( f(x)\, dx=g(y)\, dy \).

После разделения разделимые дифференциальные уравнения могут быть решены путем интегрирования обеих частей уравнения.2+х+С. \]

Как и ожидалось, существует целое семейство решений этого дифференциального уравнения.

Задача начального значения (IVT)

Задача с начальным значением представляет собой дифференциальное уравнение, которое предоставляет дополнительную информацию о начальном или начальном значении функции. Это позволяет нам найти константу и найти единственное решение.

Пример 4

Найдите решение \( y’=\frac{6x+1}{2y} \), которое удовлетворяет \( y(2)=3 \).2+х-5}. \]

Пример 5

Банк выплачивает 2% годовых по своим депозитным сертификатам, но взимает ежегодную комиссию в размере 20 долларов. Если вы изначально инвестируете 3000 долларов, сколько у вас будет через 10 лет?

Вы можете узнать это по примеру из начала раздела, для которого мы составили уравнение \( B'(t)=0,02B(t)-20 \) или, проще говоря, \[ \frac{dB {dt}=0,02B-20. \]

Мы можем разделить это уравнение, умножив на \(dt\) и разделив на все выражение справа: \[ \frac{dB}{0.02B-20}=дт. \]

Интегрирование левой части этого уравнения требует подстановки. Пусть \(u=0,02B-20\), значит, \(du=0,02\, дБ\). Произведя замену, \[ \begin{выравнивание*} \int\frac{dB}{0.02B-20}=& \int\frac{du/0.02}{u} \\ =& \int\frac{1}{u}\frac{du}{0,02} \\ =& \frac{1}{0.02}\int\frac{1}{u}\, du \\ =& \frac{1}{0.02}\ln|u|+C_1\\ =& \frac{1}{0,02}\ln|0,02B-20|+C_1 \end{выравнивание*} \]

Интегрировать правую часть дифференциального уравнения проще: \[\int dt = t+C_2\]

Вместе это дает нам общее решение дифференциального уравнения (мы также комбинируем \( C \) на этом шаге): \[ \frac{1}{0.{0,02(10)}+1000\приблизительно \$3442,81. \]

Стоит отметить, что этот ответ не совсем правильный. Дифференциальные уравнения предполагают 90 353 непрерывных 90 354 изменений, и маловероятно, что проценты непрерывно начисляются или комиссия взимается непрерывно. Однако ответ, вероятно, близок к реальному ответу, а дифференциальные уравнения дают относительно простую модель сложной ситуации.

Модели роста

Пример с банковским счетом продемонстрировал одну базовую модель роста: рост пропорционален существующему количеству.Банковские счета и население имеют тенденцию расти таким образом, если их не ограничивать. Этот тип роста называется неограниченным ростом .

Неограниченный рост

Если количество или население y растет со скоростью, пропорциональной размеру этого количества, его можно смоделировать с неограниченным ростом, который имеет дифференциальное уравнение: \[ y’=ry, \], где \(r\) — константа.

Пример 6

Население увеличивается на 8% каждый год. Если текущая численность населения составляет 5000 человек, найдите уравнение для численности населения через \(t\) лет.{0,08 т}. \]

Обратите внимание, что решение уравнения неограниченного роста является показательным уравнением.

Когда продукт активно рекламируется, продажи будут расти очень быстро, но в конце концов рынок достигнет насыщения, и продажи замедлятся. В этом типе роста, называемом ограниченным ростом , популяция растет со скоростью, пропорциональной расстоянию от максимального значения.

Ограниченный рост

Если величина растет со скоростью, пропорциональной расстоянию от максимального значения \(M\), ее можно смоделировать с ограниченным ростом, который имеет дифференциальное уравнение \[ y’=k(My), \], где \ (k\) — константа, а \(M\) — максимальный размер \(y\).

Пример 7

Представлен новый сотовый телефон. По оценкам компании, они продадут 200 тысяч телефонов. Через 1 месяц они продали 20 тысяч. Сколько они продадут через 9 месяцев?

В этом случае есть максимальное количество телефонов, которые они рассчитывают продать, поэтому \(M = 200\) тысяч. Моделируя продажи \(y\) в тысячах телефонов, мы можем написать дифференциальное уравнение \[ y’=k(200-y). \]

Так как это был новый телефон, \( y(0)=0 \).{-0,105(9)}+200\около 122,26\текст{тыс. телефонов}. \]

Ограниченный рост также обычно используется для моделей обучения, поскольку при изучении нового навыка люди обычно сначала учатся быстро, а затем скорость их совершенствования замедляется по мере приближения к мастерству.

Раньше мы использовали неограниченный рост для моделирования населения, но часто население будет ограничено едой, пространством и другими ресурсами. Когда популяция растет как пропорционально ее размеру, так и относительно расстояния от некоторого максимума, это называется логистическим ростом .Это приводит к дифференциальному уравнению \(y’=ky(M-y)\), которое является точным, но не всегда удобным в использовании. Мы будем использовать небольшую модификацию. Поскольку для решения этого дифференциального уравнения требуются методы интегрирования, которые мы не изучили, форма решения дана.

Логистический рост

Если количество растет со скоростью, пропорциональной его размеру и расстоянию от максимального значения \(M\), его можно смоделировать с помощью логистического роста , который имеет дифференциальное уравнение: \[ y’=ry\ влево(1-\frac{y}{M}\вправо).{-1,1404t}=& \ гидроразрыва {\ гидроразрыва {5} {3}-1} {49} \ приблизительно 0,01361 \\ t = & \ frac {\ ln (0,01361)} {-1,1404} \ приблизительно 3,77 \ text {лет}. \end{выравнивание*} \]

Рост логистики также является хорошей моделью для нерекламируемых продаж. Продажи нового продукта, который не рекламируется, сначала будут медленно расти, а затем расти по мере распространения молвы и знакомства людей с продуктом. Продажи будут выравниваться по мере приближения к насыщению рынка.

Дифференциальные уравнения — Введение

Дифференциальное уравнение — это уравнение с функцией и одной или несколькими ее производными:

Пример: уравнение с функцией y и ее производная ды дх  

Решение

Мы решим его, когда найдем функцию y (или набор функций y).

Есть много «приемов» решения дифференциальных уравнений (, если их можно решить!).

Но сначала: почему?

Чем полезны дифференциальные уравнения?

В нашем мире вещи меняются, и , описывающее, как они меняются, часто заканчивается дифференциальным уравнением:

Пример: Кролики!

Чем больше у нас будет кроликов, тем больше у нас будет крольчат.

Потом эти кролики вырастают и тоже рожают! Население будет расти все быстрее и быстрее.

Важными частями этого являются:

• население N в любое время т
• скорость роста р
• скорость изменения населения dN dt

Думайте о dN dt как о «насколько население меняется с изменением времени в любой момент времени».

Представим, что скорость роста r равна 0.01 новых кроликов в неделю за каждого текущего кролика.

Когда популяция составляет 1000 , скорость изменения dN dt составляет 1000×0,01 = 10 новых кроликов в неделю.

Но это верно только для конкретного времени , и это не включает в себя то, что население постоянно увеличивается. Чем больше популяция, тем больше новых кроликов мы получаем!

Когда население составляет 2000 , мы получаем 2000×0.01 = 20 новых кроликов в неделю и т.д.

Таким образом, лучше сказать, что скорость изменения (в любой момент) равна скорости роста, умноженной на численность населения в этот момент:

дН дт = рН

И это Дифференциальное уравнение , потому что оно имеет функцию N(t) и ее производную.

 

А как сильна математика! В этом коротком уравнении говорится, что «скорость изменения численности населения с течением времени равна скорости роста, умноженной на численность населения».

Дифференциальные уравнения

могут описать, как меняется население, как перемещается тепло, как вибрируют пружины, как распадается радиоактивный материал и многое другое. Это очень естественный способ описать многие вещи во Вселенной.

Что с ними делать?

Дифференциальное уравнение само по себе является прекрасным способом что-то выразить, но его трудно использовать.

Итак, мы пытаемся решить их, превратив дифференциальное уравнение в более простое уравнение без дифференциальных битов, чтобы мы могли выполнять вычисления, строить графики, предсказывать будущее и так далее.

Пример: сложные проценты

Деньги приносят проценты. Проценты могут рассчитываться в фиксированное время, например, ежегодно, ежемесячно и т. д., и добавляться к исходной сумме.

Это называется сложным процентом.

Но когда он начисляется непрерывно , то в любой момент проценты добавляются пропорционально текущей стоимости кредита (или инвестиции).

И по мере роста кредита проценты по нему увеличиваются.

Использование t для времени, r для процентной ставки и V для текущей стоимости кредита:

dV dt = rV

 

А вот и крутая вещь: это то же самое уравнение, которое мы получили с Кроликами! Просто там разные буквы.Итак, математика показывает нам, что эти две вещи ведут себя одинаково.

 

Решение

Дифференциальное уравнение говорит об этом хорошо, но его трудно использовать.

Но не волнуйтесь, это можно решить (используя специальный метод разделения переменных) и получить:

В = ПЭ ^рт

Где P — основная сумма (первоначальный заем), а e — число Эйлера.

Таким образом, непрерывно начисляемый кредит в размере 1000 долларов США на 2 года с процентной ставкой 10% становится:

В = 1000 × e ^{(2 × 0.1)}

В = 1000 × 1,22140…

V = 1221,40 доллара США (с точностью до цента)

Итак, дифференциальные уравнения отлично описывают вещи, но их нужно решать, чтобы они были полезными.

Дополнительные примеры дифференциальных уравнений

Уравнение Ферхюльста

Пример: Снова кролики!

Помните о нашем росте Дифференциальное уравнение:

дН дт = рН

Ну, этот рост не может продолжаться вечно, так как скоро у них закончится доступная еда.

Итак, давайте улучшим его, включив:

• максимальное население, которое может поддерживать еда k

Парень по имени Ферхулст все понял и получил дифференциальное уравнение:

dN dt = rN(1−N/k)

Уравнение Ферхюльста

Простое гармоническое движение

В физике простое гармоническое движение — это тип периодического движения, при котором восстанавливающая сила прямо пропорциональна смещению.Примером этого является масса на пружине.

Пример: пружина и груз

К пружине прикреплен груз:

• груз опускается под действием силы тяжести,
• по мере растяжения пружины ее натяжение увеличивается,
• вес замедляется,
• затем натяжение пружины тянет его обратно,
• , затем он падает вниз, вверх и вниз, снова и снова.

Опиши это математически!

 

Груз притягивается вниз под действием силы тяжести, и из второго закона Ньютона мы знаем, что сила равна массе, умноженной на ускорение:

F = м а

А ускорение есть вторая производная положения по времени, поэтому:

F = м d ² x dt ²

 

Пружина тянет ее обратно в зависимости от того, насколько она растянута ( k — жесткость пружины, а x — степень ее растяжения): F = -kx

Две силы всегда равны:

м d ² x dt ² = −kx

У нас есть дифференциальное уравнение!

Имеет функцию x(t) и вторую производную г ² х дт ²

 

Примечание: мы не включили «демпфирование» (замедление отскоков из-за трения), что немного сложнее, но вы можете поиграть с ним здесь (нажмите play ):

 

Создание дифференциального уравнения является первым важным шагом.Но нам также нужно решить , чтобы узнать, как, например, пружина подпрыгивает вверх и вниз с течением времени.

Классифицируйте, прежде чем пытаться решить

Так как же нам решить их?

Это не всегда просто!

За годы работы мудрые люди разработали специальных методов для решения некоторых типов дифференциальных уравнений.

Итак, нам нужно сначала узнать какой тип дифференциального уравнения.

Это как путешествие: разные виды транспорта решили, как добраться до определенных мест. Это близко, так что мы можем просто пройтись? Есть ли дорога, чтобы мы могли взять машину? Или он находится в другой галактике, и мы просто пока не можем туда добраться?

Итак, давайте сначала классифицируем дифференциальное уравнение .

 

Обычный или частичный

Первая основная группа:

• «Обычные дифференциальные уравнения» (ОДУ) имеют единственную независимую переменную (например, y )
• «Уравнения с частными производными» (УЧП) имеют две или более независимых переменных.

Мы изучаем обыкновенных дифференциальных уравнений здесь!

 

Орден и степень

Далее прорабатываем Орден и Степень:

Заказ

Орден является высшей производной (это первая производная? вторая производная? и т.д.):

Пример:

dy dx + y ² = 5x

Имеет только первую производную ды дх , так и «Первый Орден»

Пример:

d ² y dx ² + xy = sin(x)

Имеет вторую производную г ² г дх ² , так и «Заказ 2»

Пример:

d ³ y dx ³ + x dy dx + y = e ^x

Имеет третью производную г ³ г дх ³ который превосходит ды дх , так и «Заказ 3»

Степень

Степень является показателем старшей производной.

Пример:

( dy dx ) ² + y = 5x ²

Наивысшая производная — это просто dy/dx, и ее показатель степени равен 2, так что это «вторая степень»

На самом деле это обыкновенное дифференциальное уравнение первого порядка второй степени

Пример:

d ³ y dx ³ + ( dy dx ) ² + y = 5x ²

Высшая производная d ³ y/dx ³ , но у нее нет показателя степени (на самом деле, степени 1, которая не показана), так что это «Первая степень».

(Показатель степени 2 для dy/dx не считается, так как это не самая высокая производная).

Итак, это обыкновенное дифференциальное уравнение первой степени третьего порядка

 

Будьте осторожны, не путайте порядок со степенью. Некоторые люди используют порядок слов, когда имеют в виду степень!

Линейный

Это Линейная , когда переменная (и ее производные) не имеет степени или другой функции, наложенной на нее.

So no y ² , y ³ , √y, sin(y), ln(y) и т.д.,
просто y (или любая другая переменная)

Более формально Линейное дифференциальное уравнение имеет форму:

dy dx + P(x)y = Q(x)

Решение

Хорошо, мы классифицировали наше дифференциальное уравнение, теперь нужно решить его.

И у нас есть руководство по решению дифференциальных уравнений, чтобы помочь вам.

 

Лаборатория дифференциального анализатора

Дифференциальный анализатор (ДА) — это механическое устройство, которое решает дифференциальные уравнения, моделируя их на физических компонентах. DA широко использовались в первой половине 20-го века, до того, как цифровые компьютеры смогли решать дифференциальные уравнения. Сегодня DA по-прежнему полезны, поскольку позволяют нам «увидеть» то, как решение дифференциального уравнения меняется с течением времени.Абстрактные изменения математических величин можно визуализировать в физических движениях и вращениях в рамках DA .

Ключевым компонентом DA является интегратор , механическое устройство, которое принимает механическое представление производной в качестве входных данных и возвращает механическое представление чистого изменения в качестве выходных данных. Количество интеграторов в DA говорит о том, какие дифференциальные уравнения он может решать. DA с двумя интеграторами может решать одно ОДУ второго порядка или систему из двух ОДУ первого порядка . DA с четырьмя интеграторами может решить систему из двух ОДУ второго порядка или одного ОДУ второго порядка с принудительным членом, который сам является решением ОДУ второго порядка .

Узнайте больше о дифференциальных анализаторах в Википедии.

 

Изображения лаборатории дифференциального анализатора

---

Кафедра математики – двухинтегратор Дифференциальный анализатор по прозвищу «Лиззи».

---

Дифференциальный анализатор полностью аналоговый.Результат состоит из графика решения, нарисованного на бумаге.

---

Два интегратора на главном четырехинтеграторном дифференциальном анализаторе лаборатории, прозванном «Искусство» в честь Артура Портера.

---

Вид сверху на «Искусство».

 

Свяжитесь с нами по поводу лаборатории дифференциальных анализаторов:

Доктор Бонита Лоуренс
Офис: Smith Hall 614

Лаборатория дифференциального анализатора
Местонахождение: Smith Hall 614
Телефон: 304-696-3854

 

Разница между дифференциалом и производной

Чтобы лучше понять разницу между дифференциалом и производной функции, необходимо сначала понять концепцию функции.

Функция — это одно из основных понятий математики, определяющее отношение между набором входных данных и набором возможных выходных данных, где каждый вход связан с одним выходом. Одна переменная является независимой переменной, а другая переменная является зависимой переменной.

Понятие функции — одна из самых недооцененных тем в математике, но она необходима для определения физических взаимосвязей. Возьмем, к примеру, утверждение «у есть функция от х» означает, что что-то, связанное с у, напрямую связано с х по некоторой формуле.Допустим, если на входе 6 и функция состоит в том, чтобы добавить 5 к входу 6. Результат будет 6 + 5 = 11, что и является вашим выходом.

В математике есть несколько исключений или можно сказать задачи, которые не могут быть решены обычными методами геометрии и алгебры. Для решения этих задач используется новая область математики, известная как исчисление.

Исчисление коренным образом отличается от математики, которая не только использует идеи геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.

Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других разделов математики. Дифференциальное — это подполе исчисления, относящееся к бесконечно малой разнице в некоторой переменной величине и являющееся одним из двух фундаментальных разделов исчисления. Другая ветвь называется интегральным исчислением.

 

Что такое дифференциал?

Дифференциальное исчисление является одним из основных разделов исчисления, наряду с интегральным исчислением.Это подполе исчисления, которое имеет дело с бесконечно малыми изменениями в некоторой переменной величине. Мир, в котором мы живем, полон взаимосвязанных величин, которые периодически меняются.

Например, площадь круглого тела, которая изменяется при изменении радиуса, или снаряда, скорость которого изменяется. Эти изменяющиеся объекты, в математических терминах, называются переменными, а скорость изменения одной переменной по отношению к другой является производной. А уравнение, которое представляет связь между этими переменными, называется дифференциальным уравнением.

Дифференциальные уравнения — это уравнения, содержащие неизвестные функции и некоторые их производные.

 

Что такое производная?

Понятие производной функции — одно из самых мощных понятий в математике. Производная функции обычно представляет собой новую функцию, которая называется функцией производной или функцией скорости.

Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной по отношению к изменению значения независимой переменной.Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной. Он измеряет, насколько крутым является график функции в некоторой заданной точке графика.

Проще говоря, производная — это скорость, с которой функция изменяется в определенной точке.

 

Разница между дифференциалом и производной

Определение дифференциала Vs. Производная

Термины «дифференциал» и «производный» тесно связаны друг с другом с точки зрения взаимосвязи.В математике изменяющиеся объекты называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.

Уравнения, определяющие связь между этими переменными и их производными, называются дифференциальными уравнениями. Дифференциация – это процесс нахождения производной. Производная функции — это скорость изменения выходного значения по отношению к ее входному значению, тогда как дифференциал — это фактическое изменение функции.

Связь дифференциала с.Производная

Дифференцирование — это метод вычисления производной, которая представляет собой скорость изменения выходного сигнала y функции по отношению к изменению переменной x.

Проще говоря, производная относится к скорости изменения y по отношению к x, и это соотношение выражается как y = f(x), что означает, что y является функцией x. Производная функции f(x) определяется как функция, значение которой порождает наклон f(x), где она определена и f(x) дифференцируема.Это относится к наклону графика в данной точке.

Представление дифференциала против. Производная

Дифференциалы представлены как d x, d y, d t и т. д., где d x представляет небольшое изменение x, d y представляет небольшое изменение y, а d t — небольшое изменение t. При сравнении изменений связанных величин, где y является функцией x, дифференциал d y можно записать как:

d у = f ^’ (х) d х

Производная функции представляет собой наклон функции в любой точке и записывается как d / d x.Например, производная sin(x) может быть записана как:

d / d x sin(x) = sin(x) ^’ = cos(x)

Дифференциал и производная: сравнительная таблица

 

Резюме Дифференциал Vs. Производная

В математике скорость изменения одной переменной по отношению к другой называется производной, а уравнения, выражающие связь между этими переменными и их производными, называются дифференциальными уравнениями.Короче говоря, дифференциальные уравнения включают производные, которые фактически определяют, как одна величина изменяется по отношению к другой. Решив дифференциальное уравнение, вы получите формулу величины, не содержащую производных. Метод вычисления производной называется дифференцированием. Проще говоря, производная функции — это скорость изменения выходного значения по отношению к ее входному значению, тогда как дифференциал — это фактическое изменение функции.

Сагар Хиллар — плодовитый автор контента/статей/блогов, работающий старшим разработчиком/писателем контента в известной фирме по обслуживанию клиентов, базирующейся в Индии.У него есть стремление исследовать разносторонние темы и разрабатывать высококачественный контент, чтобы сделать его лучше всего читаемым. Благодаря своей страсти к писательству, он имеет более 7 лет профессионального опыта в написании и редактировании текстов на самых разных печатных и электронных платформах.

Вне своей профессиональной деятельности Сагар любит общаться с людьми из разных культур и происхождения. Можно сказать, что он любопытен по натуре. Он считает, что каждый — это опыт обучения, и это приносит определенное волнение, своего рода любопытство, чтобы продолжать идти.Поначалу это может показаться глупым, но через какое-то время это расслабит вас и вам будет легче начать разговор с совершенно незнакомыми людьми — вот что он сказал». : Если вам понравилась эта статья или наш сайт. Пожалуйста, распространите информацию. Поделитесь им с друзьями/семьей.

См.
APA 7
Хиллар, С. (2018, 20 сентября). Разница между дифференциалом и производной. Разница между похожими терминами и объектами.http://www.differencebetween.net/science/mathematics-statistics/difference-between- Differential-and-derivative/.
MLA 8
Хиллар, Сагар. «Разница между дифференциалом и производной». Разница между похожими терминами и объектами, , 20 сентября 2018 г., http://www.differencebetween.net/science/mathematics-statistics/difference-between- Differential-and-derivative/.