Высота проведенная из вершины прямого угла равна: Высота в прямоугольном треугольнике. Свойства. Как найти?

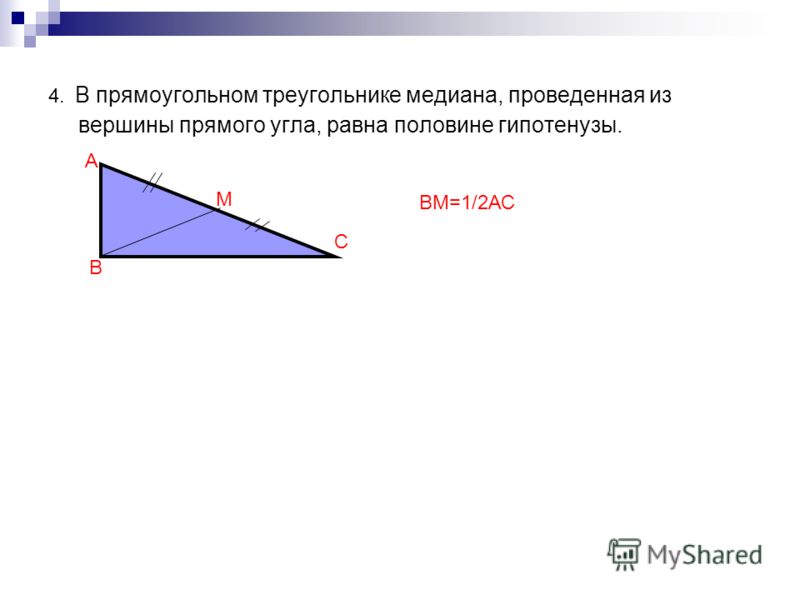
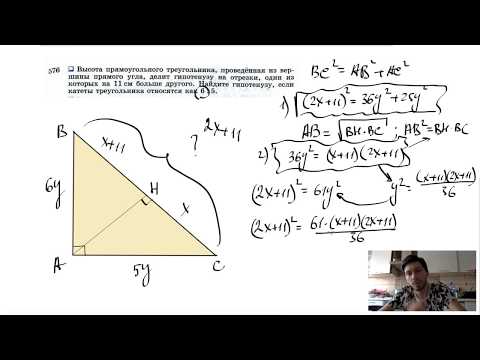
из прямого угла и острого

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые (<90°).

• Свойства высоты в прямоугольном треугольнике
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
• Пример задачи

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

1. △ABD ∼ △ABC по двум равным углам: ∠ADB = ∠BAC (прямые), ∠ABD = ∠ABC.

2. △ADC ∼ △ABC по двум равным углам: ∠ADC = ∠BAC (прямые), ∠ACD = ∠ACB.

3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC.
Следовательно, ∠BAD = ∠ACD.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c² = a² + b² = 9² + 12² = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Поиск по сайту:

Справочник по математике

Геометрия (Планиметрия)

Треугольники

Фигура	Рисунок	Формулировка
Прямоугольный треугольник		Треугольник, у которого один из углов равен 90°, называют прямоугольным треугольником. Сторону, лежащую против угла в 90°, называют гипотенузой, две другие стороны называют катетами.
Катеты прямоугольного треугольника		Длины катетов прямоугольного треугольника меньше длины гипотенузы.
Равнобедренный прямоугольный треугольник		Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Острые углы равнобедренного прямоугольного треугольника равны 45°.
Прямоугольный треугольник с углом в 30°		Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Катет, равный половине гипотенузы		Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°.
Медиана, проведённая к гипотенузе прямоугольного треугольника		Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Посмотреть доказательство
Медиана треугольника, равная половине стороны, к которой она проведена		Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.
Центр описанной окружности		Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Посмотреть доказательство
		Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.
Теорема Пифагора		В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2 Посмотреть доказательство
Обратная теорема Пифагора		Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Прямоугольный треугольник

Определение прямоугольного треугольника: Треугольник, у которого один из углов равен 90°, называют прямоугольным треугольником. Сторону, лежащую против угла в 90°, называют гипотенузой, две другие стороны называют катетами. Свойство катетов прямоугольного треугольника: Длины катетов прямоугольного треугольника меньше длины гипотенузы.

Равнобедренный прямоугольный треугольник

Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45°.

Прямоугольный треугольник с углом в 30°

Свойство прямоугольного треугольника с углом в 30°: Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30°: Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°.

Медиана, проведённая к гипотенузе прямоугольного треугольника

Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Посмотреть доказательство Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

Центр описанной окружности

Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Посмотреть доказательство Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

Теорема Пифагора

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2 Посмотреть доказательство Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

До ЕГЭ по математике осталось
дней	часов	минут	секунд

./ris/b1_45.gif»>НАШИ ПАРТНЕРЫ «НПО Астек» «Fastvideo» Бюро переводов «Медтран» Независимый бизнес-консультант Е.Самаров

Что такое высота треугольника? Определение, формулы и примеры

Высота треугольника — это отрезок перпендикулярной линии, проведенный из вершины к противоположной стороне треугольника. Он может лежать внутри или снаружи треугольника, в зависимости от типов треугольников. Высота треугольника в основном определяет высоту, когда мы должны измерить площадь треугольника по отношению к основанию.

Содержание: Определение Использовать Свойства Высота треугольников Тупоугольный треугольник Равносторонний треугольник Прямоугольный треугольник Равнобедренный треугольник Формулы Медиана против высоты Решенные примеры Практические задачи Часто задаваемые вопросы

Что такое высота треугольника?

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне. Также известная как высота треугольника, высота образует прямоугольный треугольник с основанием. Ниже приведено изображение, показывающее высоту треугольника.

Какая польза от высоты треугольника?

Основным применением высоты является то, что она используется для расчета площади треугольника, т. е. площадь треугольника равна (½ основания × высота). Теперь, используя площадь треугольника и его высоту, можно легко вычислить основание как Основание = [(2 × Площадь)/Высота]

Свойства высоты треугольника

Различные свойства высоты треугольника перечислены ниже:

• Треугольник может иметь максимум три высоты
• Высота треугольника перпендикулярна противоположной стороне. Таким образом, он образует угол 90 градусов с противоположной стороной.
• В зависимости от типа треугольника высота может лежать внутри или снаружи треугольника
• Точка пересечения трех высот называется ортоцентром треугольника

Высоты различных треугольников

О высоте: разные треугольники имеют разные типы высоты.

Ниже приведен обзор различных типов высот в различных треугольниках.

Для тупоугольного треугольника высота находится вне треугольника. У таких треугольников основание продлевается, а затем из противоположной вершины к основанию проводится перпендикуляр. Для тупоугольного треугольника высота показана в треугольнике ниже.

Высота тупоугольного треугольника

Высота равностороннего треугольника

Высота или высота равностороннего треугольника — это отрезок прямой от вершины, перпендикулярной противоположной стороне. Интересно отметить, что высота равностороннего треугольника делит пополам его основание и противолежащий угол. На изображении ниже показан равносторонний треугольник ABC, где BD — высота (h), AB = BC = AC, ∠ABD = ∠CBD и AD = CD.

В равностороннем треугольнике все углы равны 60°.

В треугольнике ADB,

sin 60° = h/AB

Мы знаем, что AB = BC = AC = s (поскольку все стороны равны)

∴ sin 60° = ч/с

√3/2 = ч/с

ч = (√3/2)с

Следовательно, высота равностороннего треугольника = h = (√3/2) × s

Высота прямоугольного треугольника

Высота прямоугольного треугольника делит существующий треугольник на два подобных треугольника. Согласно Теорема о высоте прямоугольного треугольника , высота на гипотенузе равна среднему геометрическому отрезков, образованных высотой на гипотенузе.

В прямоугольном треугольнике при проведении перпендикуляра из вершины к гипотенузе образуются два подобных прямоугольных треугольника. Это называется теоремой о высоте прямоугольного треугольника.

На приведенном выше рисунке

△АДБ ∼ △БДК

Таким образом,

AD/BD = BD/DC

BD2 = AD.DC

ч3 = х, у

ч = √xy

Следовательно, высота прямоугольного треугольника.

Высота равнобедренного треугольника

Высота равнобедренного треугольника делит пополам угол вершины и основание. Следует отметить, что равнобедренный треугольник — это треугольник с двумя конгруэнтными сторонами, поэтому высота делит пополам основание и вершину.

Высоты Треугольников Формулы

Треугольный	Формула высоты
Равносторонний треугольник	ч = (½) × √3 × с
Равнобедренный треугольник	ч =√(а 2 −b 2 /4)
Прямоугольный треугольник	ч =√(ху)

Разница между медианой и высотой треугольника

Медиана треугольника	Высота треугольника
Медиана — это отрезок, проведенный от вершины к середине противоположной стороны треугольника.	Высота отсчитывается от вершины и перпендикулярна противоположной стороне треугольника
Делит противоположную сторону пополам	Он может делить или не делить противоположную сторону пополам в зависимости от типа треугольника
Всегда лежит внутри треугольника	Может лежать или не лежать внутри треугольника, в зависимости от типа треугольника
Делит треугольник на две равные части	Не делит треугольник на две равные части
Точка пересечения трех медиан называется центром треугольника	Точка пересечения трех высот называется ортоцентром треугольника

Решенные примеры

Q.1: Какова высота равностороннего треугольника, если длина его стороны равна 4 см?

Решение: Дана длина стороны равностороннего треугольника 4 см.

Высота равностороннего треугольника, h = s√3/2

= 4√3/2

= 2√3 см

Q. 2: Если стороны треугольника a = 3, b = 6 и c = 7, то какова высота треугольника?

Решение: Так как все стороны данного треугольника неравны по длине, то это разносторонний треугольник.

Используя формулу высоты разностороннего треугольника, имеем;

ч = [2√(s(s−a).(s−b).(s−c))]/b

с = (а+b+с)/2 = (3+6+7)/2 = 16/2 = 8

ч = [2√(8(8-3)(8-6)(8-7))]/2

ч = [2√(8.5.2.1)]/2

ч = 4√5

Практические вопросы

1. Какова высота равнобедренного треугольника, если длина равных сторон 8 см, а неравных 6 см?
2. Три стороны данного треугольника равны 8 единицам, 11 единицам и 13 единицам. Найдите длину высоты треугольника.
3. Найдите высоту равностороннего треугольника, сторона которого равна 10 см.

Связанные статьи

• Треугольники
• Площадь треугольника
• Высота и медиана треугольника
• Равнобедренный треугольник
• Прямоугольный треугольник
• Равносторонний треугольник

Часто задаваемые вопросы – Часто задаваемые вопросы

Что такое высота треугольника?

Высота треугольника — это расстояние по перпендикуляру, проведенное из вершины к противоположной стороне треугольника.

Какова формула высоты треугольника?

Формула высоты треугольника различается для разных треугольников.
Для разностороннего треугольника высота равна [2√(s(s−a).(s−b).(s−c))]/b
Для равностороннего треугольника высота равна a√3/2
Для высота равнобедренного треугольника √(a ² – b ² /4)
Для прямоугольного треугольника высота равна √xy

Где находится высота остроугольного треугольника?

Высота остроугольного треугольника лежит внутри треугольника.

Какое свойство высоты треугольника?

Высота треугольника лежит внутри или вне треугольника. Он находится под углом 90 градусов к противоположной стороне. Точка пересечения трех высот называется ортоцентром треугольника.

Находится ли высота тупоугольного треугольника внутри треугольника?

Нет, высота тупоугольного треугольника лежит вне треугольника.

Продолжайте посещать BYJU’S, чтобы изучать различные темы по математике интересным и эффективным способом. Кроме того, зарегистрируйтесь сейчас и загрузите BYJU’S — The Learning App, чтобы получать увлекательные видеоуроки и персонализированные обучающие программы.

Объяснение урока: Медианы треугольников

В этом объяснении мы научимся определять медианы треугольника и использовать их свойства пропорциональности, чтобы найти недостающую длину.

Медианы треугольников — это специальные линии с особыми свойствами. Давайте начнем с определением медианы.

Определение: медиана

Медианы треугольника — это три отрезка, идущие от каждой вершины к середина противоположной стороны.

На следующей диаграмме показан пример, содержащий медиану треугольника и две другие линии в треугольнике, которые не являются медианами.

Так как в треугольнике 3 вершины, то и 3 медианы. Когда мы рисуем все мы видим, что все они пересекаются. Это общее свойство медиан которые мы изложим в следующей теореме.

Теорема: совпадение медиан треугольника

Три медианы треугольника пересекаются в одной точке (то есть они параллельны). Точка их пересечения называется точкой совпадение медиан.

Другое свойство медиан треугольника состоит в том, что относительное положение точка пересечения медиан всегда одна и та же. Действительно, точка совпадение расположено на двух третях длины медианы от вершина.

Давайте представим себе это. Мы можем разделить каждую медиану на три трети, как показано на диаграмма. Две трети находятся между вершиной и точкой пересечения, и одна треть находится между точкой пересечения и серединой сторона.

Эквивалентно это означает, что длина отрезка между вершиной и точка совпадения в два раза больше, чем между точкой совпадения и середина противоположной стороны.

Это можно найти и с помощью алгебры.

Если 𝐴𝑃=23⋅𝐴𝐸 и 𝑃𝐸=13⋅𝐴𝐸, то из второго уравнения (умножая обе части на 3) получаем 𝐴𝐸=3𝑃𝐸, и заменив 𝐴𝐸 на 3𝑃𝐸 в первое уравнение, получаем 𝐴𝑃=23⋅3𝑃𝐸, что дает 𝐴𝑃=2𝑃𝐸.

Подведем итоги.

Теорема: положение точки пересечения медиан треугольника

Расстояние от каждой вершины треугольника до точки пересечения его medians составляет две трети длины медианы от этой вершины.

Эквивалентно расстоянию от точки пересечения медиан до вершина в два раза больше, чем расстояние до противоположной средней точки.

Давайте посмотрим на наш первый пример, где нам нужно использовать свойство, указанное в эта теорема о положении точки пересечения медиан треугольник.

Пример 1: Свойства точки пересечения медиан треугольника

В треугольнике 𝐴𝐵𝐶 𝑀 является точкой совпадение его медиан. Если 𝐴𝐷 медиана, тогда 𝐴𝑀=𝑀𝐷.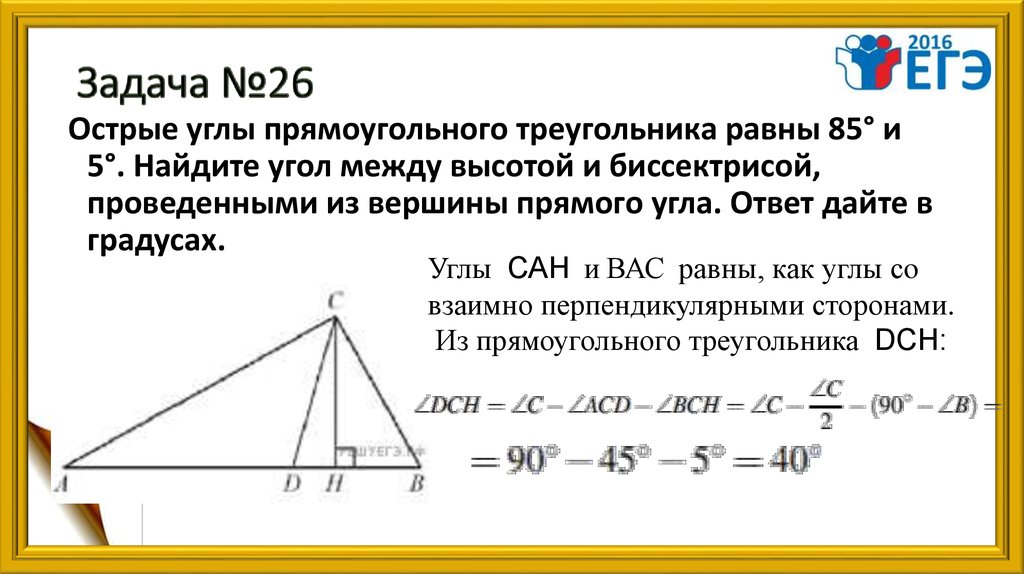

Ответ

Напомним, что медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны. Нарисуем все медианы треугольник 𝐴𝐵𝐶 с точкой 𝑀 совпадение. 𝐴𝐷 — медиана, соединяющая вершину 𝐴 с 𝐷; следовательно, 𝐷 — середина стороны 𝐵𝐶.

Мы знаем из теоремы о точке пересечения трех медиан треугольника, что расстояние от каждой вершины до точки пересечения медиан составляет две трети длины медианы от этой вершины. Это значит у нас тут 𝐴𝑀=23𝐴𝐷.

Это означает, что если мы разрежем 𝐴𝐷 на три равных сегмента, 𝐴𝑀 будет сделан из двух из них. Следует, что 𝑀𝐷 состоит из третьего. Поэтому, 𝐴𝑀 в два раза длиннее 𝑀𝐷.

Следовательно, 𝐴𝑀=2𝑀𝐷.

Во втором примере нам нужно определить медианы, а затем использовать свойство точка пересечения медиан, чтобы найти длину от вершины до точки согласия.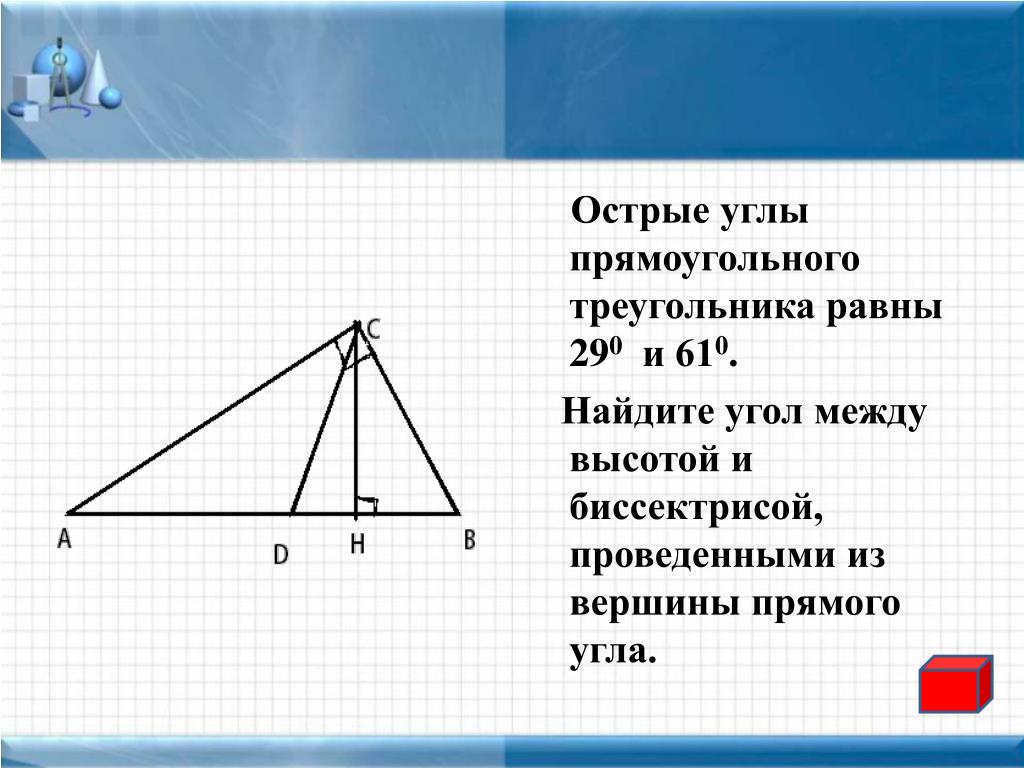

Пример 2. Определение медиан и использование свойства их точки пересечения с Найдите недостающую длину

Найдите длину 𝐴𝑀, учитывая, что 𝐴𝐸=54.

Ответ

Глядя на диаграмму, мы видим, что оба 𝐴𝐸 и 𝐶𝐷 — отрезки, соединяющие вершину с середина противоположной стороны. Следовательно, 𝐴𝐸 и 𝐶𝐷 медианы треугольника 𝐴𝐵𝐶. Таким образом, точка 𝑀 является точкой совпадения медиан треугольника 𝐴𝐵𝐶.

Напомним, что длина 𝐴𝑀, т. е. расстояние от вершины до точки пересечения составляет две трети от медианы 𝐴𝐸: 𝐴𝑀=23⋅𝐴𝐸=23⋅54=36.

Таким образом, длина 𝐴𝑀 равна 36.

Теперь рассмотрим пример, где мы используем наши знания о медианах треугольник, чтобы составить и решить линейное уравнение.

Пример 3. Использование свойств точки пересечения медиан Треугольник для формирования и решения линейного уравнения

В △𝐾𝑀𝐻, 𝐾𝑄=2 и 𝑄𝑃=(5𝑥−7).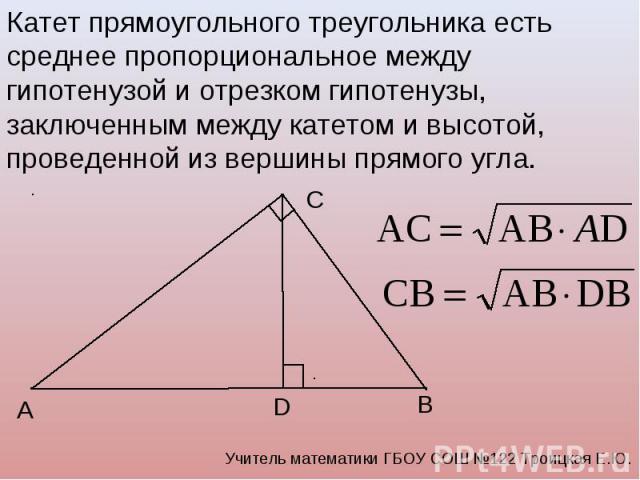 Найдите 𝑥.

Ответ

В треугольнике 𝐾𝑀𝐻 точка 𝑄 совпадение его медиан. 𝐾 является вершиной и 𝑃 — середина противоположной стороны, 𝐻𝑀. Напомним, что расстояние от каждой вершины треугольника до точки совпадение его медиан составляет две трети общей длины медианы из этой вершины. Следовательно, для медианы 𝐾𝑃 имеем 𝐾𝑄=23𝐾𝑃 и 𝑄𝑃=13𝐾𝑃.

Как 𝐾𝑄=2×13𝐾𝑃, Мы видим, что 𝐾𝑄=2𝑄𝑃.

В вопросе сказано, что 𝐾𝑄=2 и 𝑄𝑃=5𝑥−7.

Отсюда имеем 2=2(5𝑥−7).

Деление обеих частей этого уравнения на 2 дает 1=5𝑥−7.

Прибавление 7 к обеим сторонам дает 8=5𝑥.

И, наконец, разделив обе части на 5, находим, что 𝑥=85=1,6.

Теперь посмотрим на медианы прямоугольного треугольника. Помните, что право треугольник является половиной прямоугольника, как показано на следующей диаграмме, где 𝐴𝐵𝐶𝐷 — прямоугольник, а △𝐴𝐵𝐶 и △𝐶𝐷𝐴 — конгруэнтные прямоугольные треугольники.

В △𝐴𝐵𝐶, 𝐵𝐸 является медианой. В прямоугольнике 𝐴𝐵𝐶𝐷, 𝐵𝐸 составляет половину диагонали. Так как диагонали прямоугольников делят друг друга пополам (это свойство параллелограмма) и равны по длине (это свойство прямоугольники; это происходит от того, что △𝐴𝐵𝐶 и △𝐶𝐷𝐴 конгруэнтны), имеем 𝐵𝐷=𝐴𝐶, поэтому 12𝐵𝐷=12𝐴𝐶, то есть 𝐵𝐸=𝐴𝐸=𝐸𝐶.

Мы доказали следующее свойство.

Теорема: длина медианы прямоугольного треугольника

В прямоугольном треугольнике длина медианы, проведенной из вершины правого треугольника угол равен половине длины гипотенузы треугольника.

Стоит отметить, что одно из следствий этой теоремы состоит в том, что проведенная медиана из вершины прямого угла всегда делит прямоугольный треугольник на два равнобедренные треугольники.

Давайте воспользуемся этой последней теоремой в нашем следующем примере и в то же время обнаружим его следствием в специальном прямоугольном треугольнике, а именно, 30∘-60∘ прямоугольный треугольник.

Пример 4. Нахождение длины меньшей стороны прямоугольного треугольника с углами 30°-60° с помощью свойства его медианы, проведенной под прямым углом

Определите длины 𝐵𝐷 и 𝐴𝐵.

Ответ

Из диаграммы видно, что △𝐴𝐵𝐶 — прямоугольный треугольник в точке 𝐵, а поскольку 𝐷 — середина 𝐴𝐶, 𝐵𝐷 — медиана △𝐴𝐵𝐶 нарисовано под прямым углом.

Напомним, что в прямоугольном треугольнике длина медианы, проведенной из вершина прямого угла равна половине длины гипотенуза треугольника. Следовательно, у нас есть 𝐵𝐷=12𝐴𝐶=12×49=24.5.cm

Нас также просят найти длину 𝐴𝐵. Мера угла при вершине 𝐶 указана на диаграмме: это 30∘. Так как угол в 𝐵 — прямой угол, это означает, что мера угла при вершина 𝐴 равна 180−(30+90)=60∘. Кроме того, как мы нашли выше, что 𝐵𝐷=12𝐴𝐶, это означает, что 𝐵𝐷=𝐴𝐷.

Значит, △𝐴𝐵𝐷 равнобедренный, значит, два угла, образованные каждой конгруэнтной стороной и третьей стороной, равны, то есть 𝑚∠𝐴𝐵𝐷=𝑚∠𝐴=60. ∘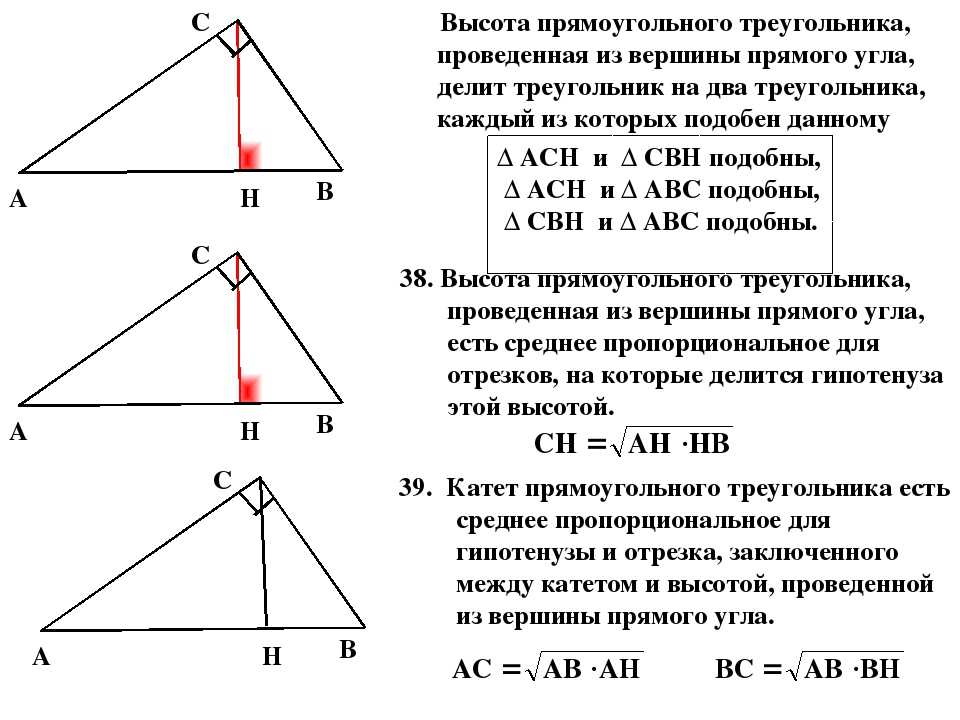

Это означает, что третий угол в △𝐴𝐵𝐷 также имеет меру 60∘ (поскольку 180−(60+60)=60∘), и поэтому △𝐴𝐵𝐷 равносторонний. Таким образом, у нас есть 𝐴𝐵=𝐵𝐷=𝐴𝐷=24.5.cm

Обратите внимание, что в последнем примере мы используем тот факт, что △𝐴𝐵𝐷 равнобедренный, чтобы доказать, что 𝑚∠𝐴𝐵=60∘. Мы могли бы также заметили, что △𝐵𝐷𝐶 равнобедренный, Который означает, что 𝑚∠𝐷𝐵𝐶=𝑚∠𝐶=30.∘

Отсюда, как 𝑚∠𝐴𝐵𝐷=90−30=60.∘

Подытожим наши выводы из последнего примера.

Теорема: Длина меньшей стороны в прямоугольном треугольнике 30°-60°

В треугольнике 30°-60° прямоугольного треугольника, длина меньшей стороны (т. е. стороны, противоположной угол 30∘) равен половине длина гипотенузы треугольника.

В нашем последнем примере мы будем использовать свойства медиан и их точку согласие на решение задачи по геометрии.

Пример 5. Нахождение периметра треугольника с помощью медиан треугольника

Учитывая, что 𝐴𝐷=9см и 𝐸𝐵=𝐴𝐵, найдите периметр △𝑀𝐷𝐸.

Ответ

Нас попросили найти периметр △𝑀𝐷𝐸. Заметим, что длины 𝐶𝐷 и 𝐷𝐵 отмечены на диаграмме как равны, поэтому 𝐷 является средней точкой. Сходным образом, 𝐶𝐸=𝐸𝐴, поэтому 𝐸 также является средней точкой. Следовательно, 𝐸𝐷 — это отрезок, соединяющий середины двух сторон △𝐴𝐵𝐶, а 𝐴𝐷 и 𝐵𝐸, которые соединяют каждую вершину △𝐴𝐵𝐶 с середина противоположной стороны, две медианы △𝐴𝐵𝐶.

Напомним, что теорема о середине треугольника утверждает, что отрезок, соединяющий середины двух сторон треугольника параллельны третьей стороне и равны половину своей длины. 𝐸𝐷 поэтому параллелен 𝐴𝐵 и составляет половину его длины; то есть половина от 12 см, или 6 см.

Теперь мы можем найти длину 𝑀𝐸 и 𝑀𝐷, вспомнив, что расстояние от каждого вершины треугольника до точки пересечения его медиан составляет две трети длина медианы от этой вершины. Отсюда следует, что расстояние от точки совмещения с серединой одной стороны составляет одну треть длины медиана от вершины, противоположной этой стороне. Следовательно, у нас есть 𝑀𝐸=13𝐸𝐵 и 𝑀𝐷=13𝐴𝐷.

Дано, что 𝐸𝐵=𝐴𝐵 и указано на на схеме 𝐴𝐵=12см. Следовательно, 𝐸𝐵=12см. Нам также дано, что 𝐴𝐷=9см. Подставляя эти значения в приведенные выше уравнения, мы получаем 𝑀𝐸=13×12=4см и 𝑀𝐷=13×9=3.cm

Чтобы найти периметр △𝑀𝐷𝐸, нам нужно чтобы сложить длины его трех сторон следующим образом: Периметрсм=𝐸𝐷+𝑀𝐸+𝑀𝐷=6+4+3=13.

Давайте теперь обобщим то, что мы узнали в этом объяснителе.

Ключевые точки

• Медианы треугольника — это три отрезка, идущие от каждой вершины к середина противоположной стороны.
• Три медианы треугольника пересекаются в одной точке: мы говорим, что они одновременны. Точка их пересечения называется точкой совпадение медиан.

  No related posts.