Динамометрический ключ КМШ-140 НИЗ 2774-140 предназначен для затягивания болтов и гаек с заранее установленным усилием. Посадочное место данного ключа 1/2 дюйма. При затягивании стрелка остается на месте, а корпус со шкалой инструмента смещается, что позволяет точно определить рабочие параметры. Предел допускаемой относительной погрешности: +-6%.
Этот товар из подборокКомплектация *
Параметры упакованного товара Единица товара: Штука Длина, мм: 423
Произведено
Указанная информация не является публичной офертой Отзывы о НИЗ КМШ-140Оставить свой отзыв На данный момент для этого товара нет расходных материаловСпособы получения товара в МосквеДоставка Вес брутто товара: 0.76 кг В каком городе вы хотите получить товар? выберите городАбаканАксайАктауАлександровАлыкельАльметьевскАнадырьАнгарскАрзамасАрмавирАрсеньевАртемАрхангельскАстраханьАхтубинскАчинскБалаковоБалашовБалезиноБарнаулБатайскБелгородБелогорскБерезникиБийскБиробиджанБлаговещенскБодайбоБокситогорскБорБорисоглебскБратскБрянскБугульмаБугурусланБуденновскБузулукВеликие ЛукиВеликий НовгородВеликий УстюгВельскВитебскВладивостокВладикавказВладимирВолгоградВолгодонскВолжскВолжскийВологдаВолховВольскВоркутаВоронежВоскресенскВыборгВыксаВышний ВолочекВязьмаВятские ПоляныГеоргиевскГлазовГорно-АлтайскГрозныйГубкинскийГусь-ХрустальныйДальнегорскДедовскДербентДзержинскДимитровградДмитровДонецкДудинкаЕвпаторияЕгорьевскЕкатеринбургЕлецЕссентукиЗаводоуковскЗеленодольскЗлатоустЗубовоИвановоИгнатовоИжевскИзбербашИнтаИркутскИшимЙошкар-ОлаКазаньКалининградКалугаКаменск-УральскийКаменск-ШахтинскийКамень-на-ОбиКанашКанскКарагандаКарасукКаргопольКемеровоКерчьКинешмаКиришиКировКиселевскКисловодскКлинКлинцыКоломнаКолпашевоКомсомольск-на-АмуреКоролевКостромаКотласКраснодарКрасноярскКропоткинКудьмаКузнецкКуйбышевКумертауКунгурКурганКурскКызылЛабинскЛабытнангиЛаговскоеЛангепасЛенинск-КузнецкийЛесосибирскЛипецкЛискиЛуневоЛюдиновоМагаданМагнитогорскМайкопМалые КабаныМахачкалаМеждуреченскМиассМинскМихайловкаМичуринскМоскваМуравленкоМурманскМуромНабережные ЧелныНадеждаНадымНазраньНальчикНаро-ФоминскНарьян-МарНаходкаНевинномысскНерюнгриНефтекамскНефтеюганскНижневартовскНижнекамскНижний НовгородНижний ТагилНовая ЧараНовозыбковНовокузнецкНовороссийскНовосибирскНовочебоксарскНовочеркасскНовый УренгойНогинскНорильскНоябрьскНурлатНяганьОбнинскОдинцовоОзерскОктябрьскийОмскОнегаОрелОренбургОрехово-ЗуевоОрскПавлодарПангодыПензаПермьПетрозаводскПетропавловскПетропавловск-КамчатскийПикалевоПлесецкПолярныйПригородноеПрокопьевскПсковПятигорскРеутовРоссошьРостов-на-ДонуРубцовскРыбинскРязаньСалаватСалехардСамараСанкт-ПетербургСаранскСарапулСаратовСаянскСвободныйСевастопольСеверныйСеверобайкальскСеверодвинскСеверскСерпуховСимферопольСлавянск-на-КубаниСмоленскСоликамскСочиСтавропольСтарый ОсколСтерлитамакСургутСызраньСыктывкарТаганрогТаксимоТамбовТаштаголТверьТихвинТихорецкТобольскТольяттиТомскТуапсеТулаТуркестанТюменьУдомляУлан-УдэУльяновскУрайУральскУрюпинскУсинскУсолье-СибирскоеУссурийскУсть-ИлимскУсть-КутУсть-ЛабинскУфаУхтаФеодосияХабаровскХанты-МансийскХасавюртЧайковскийЧебоксарыЧелябинскЧеремховоЧереповецЧеркесскЧитаЧусовойШарьяШахтыЭлектростальЭлистаЭнгельсЮгорскЮжно-СахалинскЯкутскЯлтаЯлуторовскЯрославль Самовывоз: бесплатно
г. Котельники, Яничкин проезд, д. 3 пн. – пт.: 6:00 – 20:00 сб. – вс.: 9:00 – 18:00 В корзинуул. Борисовские пруды, д. 26 пн. – вс.: 10:00 – 20:00 В корзинуул. Перерва, д. 54 пн. – вс.: 9:00 – 20:00 В корзинуМосковская обл., р.п. Андреевка, ул. Жилинская, стр. 1 пн. – вс.: 10:00 – 21:00 В корзинуСервис от ВсеИнструменты.руМы предлагаем уникальный сервис по обмену, возврату и ремонту товара! Вернем вам деньги, если данный товар вышел из строя в течение 6 месяцев с момента покупки. Обратиться по обмену, возврату или сдать инструмент в ремонт вы можете в любом магазине или ПВЗ ВсеИнструменты.ру.Гарантия производителяГарантия производителя 18 месяцев | Может понадобиться |
Динамометрический ключ JTC 1203, 465 мм, 28-210 Нм 1/2″ DR — цена, отзывы, характеристики, фото
Кузьмин Вадим
21.04.2021
Как его открыть для ремонта храповика? Открутил два винтика, а дальше что? Институт в интернете к сожалению не нашел для этого ключа.
ВсеИнструменты
21.04.2021
Здравствуйте! Вам надо обратить в сервисный центр, адреса указаны во вкладке «гарантия».
Никита
23.12.2020
Здравствуйте, купил данный ключ у вас. Вопрос по использованию. В руководстве по эксплуатации написано, что "после работы следует установить нулевое значение для того, чтобы разгрузить пружину". Что значит, "в нулевое значение"?Это значит, установить на минимальную отметку в 28Нм или выкрутить рукоятку ключа ниже отметки 28Нм до упора?
ВсеИнструменты
24.12.2020
Здравствуйте, Никита! Установить минимально допустимое значение.
Гусев Артём
30.10.2017
Если этот ключ не закручивает болты с левой резьбой но при этом реверс есть,можно им тогда срывать болты просто как воротком без вреда инструменту?
ВсеИнструменты
31.10.2017
Здравствуйте, Гусев Артём ! Теоретически такой вид работы возможен, но Если гайки затянуты очень сильно, никто гарантии не даст, что он будет их срывать без вреда себе.
Буторин Илья
25.08.2017
Ключ для затяжки правой и левой резьбы?
ВсеИнструменты
26.08.2017
Здравствуйте, Буторин Илья !Динамометрический механизм ключа срабатывает только при затяжке болтов и гаек с правой резьбой.
Ярославский Константин
13.03.2017
Завод изготовитель гарантирует настройку ключа и поверку диапазонов момента? Какова погрешность?
ВсеИнструменты
13.03.2017
Здравствуйте, Ярославский Константин !Инструмент прошел тестирование и настрои?ку на фабрике производителя. Является высокоточным инструментом с минимальнои? погрешностью +-4%.
Евгений
13.12.2016
Здравствуйте! Подскажите, к ключу идёт индивидуальный сертификат проверки?
ВсеИнструменты
14.12.2016
Здравствуйте, Евгений! Индивидуальный сертификат проверки не входит в комплект. ВсеИнструменты.ру
Алексей
02.07.2016
Скажите ключ реверсивный?
ВсеИнструменты
04.07.2016
Здравствуйте, Алексей! Реверс в данной модели присутствует. ВсеИнструменты.ру
Динамометрический ключ KING TONY 34223-1A, 1/4″, 5-25 Нм, футляр — цена, отзывы, характеристики, 1 видео, фото
Динамометрический ключ KING TONY 34223-1A, 1/4″, 5-25 Нм, футляр внесен в госреестр средств измерений.
- Тип предельный
- Квадрат 1/4 дюйма
- Min усилие, Нм 5
- Max усилие, Нм 25
- Трещотка есть
- Поверка нет
- Материал CrV
- Номер СИ в госреестре 67026-17
- Вес, кг 0,717
- Диэлектрическое покрытие нет
- Насадки в комплекте нет
- Показать еще
Этот товар из подборок
Комплектация *
Параметры упакованного товара
Единица товара: Штука
Вес, кг: 0,71
Длина, мм: 315
Ширина, мм: 70
Высота, мм: 70
Произведено
- Тайвань — родина бренда
- Тайвань — страна производства*
- Информация о производителе
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
Динамометрический ключ 1/4″ 2,5-25 Нм Hazet 5108-3CT
Динамометрический ключ Hazet 5108-3CT.
Посадочный квадрат 1/4″
Измеряемый диапазон 2,5-25 Нм
Точность срабатывания ± 3%
Длина 234 мм
Динамометрический ключ SYSTEM 5000-3 CT -классический ключ для мастерской – Полностью новая концепция, хорошее оснащение на будущее.
Новейшая технология !
Больше никакой обратной установки на минимальное значение момента!
Третье поколение динамометрических ключей 5000-3CT: Теперь более мощные и точные !
Привод-квадрата реверсивной трещотки 1/4
Точность ± 3 % от установленной на шкале величины (в направлении операции)
Надежность:
— «Щелчок на руку» (в момент размыкания)
— «Щелчок на слух»
Сконструирован для жестких условий в мастерской.
Широкий спектр применения для контролируемой затяжки винтов при ремонте и обслуживания ТС, легковых и грузовых автомобилей, а также для разнообразного применения в промышленности и мастерской.
Оптимальное уплотнительное кольцо для защиты от попадания посторонних веществ
Набор для ремонта трещотки, ориентированный на самостоятельное выполнение монтажа
пользователем, сохраняет работоспособность инструмента в течение десятилетий
Регулировка с помощью точек фиксации для оптимального управления инструментом обеспечивает надежную и быструю установку нужного крутящего момента поворотом рукоятки
Надежная фиксация установленного значения благодаря функции блокировки на голубом поворотном кольце
Символы на замке показывают соответствующие состояние блокировки
Тригонометрическая форма голубого поворотного кольца предупреждает неконтролируемое прокручивание.
Через отверстия на фиксирующем поворотном кольце можно закрепить петлю
Удобная для считывания, контрастная шкала
Надежное считывание благодаря лазерной маркировке на шкале
Встроенный переключающий рычаг
Контроль в соответствии с DIN EN ISO 6789-2:2017
С Калибровочным сертификатом и серийным номером
Поставляется в пластиковом тубусе Нexa
Квадрат согласно DIN 3120, ISO 1174-1, DIN EN ISO 6789-2:2017
Производство: Hazet (Германия)
Больше никакой обратной установки на минимальное значение момента!
На что раньше нужно было обращать внимание в большинстве механических динамометрических ключей?
Большинство динамометрических ключей после использования или при долгом хранении нужно было устанавливать обратно на самое маленькое значение момента на шкале, чтобы разгрузить пружину сжатия.
В динамометрических ключах HAZET серии 5000 и 6000 в результате многочисленных длительных испытаний на долговечность было установлено, что для практического применения больше нет необходимости в обратной установке на минимальное значение на шкале.
Ключ к тригонометрическим формулам
Когда учащиеся 10 класса приступают к изучению формул тригонометрии, их прежде всего отпугивает их количество. Заучивать их, не зная доказательства, довольно сложно, учить доказательства –трудоемко, да и нет надобности. Поэтому хочу предложить мнемонический подход к запоминанию тригонометрических формул. Изучение предлагаю начать с внимательного рассмотрения 4 формул сложения, помещенных на странице учебника:
COS(-?) =COSCOS? + SINSIN
COS(+) =CosCOS — SINSIN
SIN( –) = SINCOS — COSSIN
SIN( +) = SINCOS + COSSIN
После внимательного изучения можно сделать следующий вывод: если слева стоит косинус, то после знака « = » стоят произведения одноименных функций: COSCOS и SINSIN, кроме этого замечаем, что знак, стоящий в левой части, противоположен знаку в правой части, т. е. произошла смена знака. Если слева стоит SIN, то после знака равно стоят произведения разноименных функций: SINCOS и, проведя аналогичные рассуждения относительно знака, делаем вывод, что знак в левой и в правой части одинаковый т. е. сохраняется. Итак, подведем итог наших наблюдений.
1 — Косинус берет функции одноименные и знак меняет.
2 — Синус берет функции разноименные, знак не меняет.
После этих рассуждений и сделанных выводов предложить записать эти 4 формулы на доске (можно к доске пригласить 3,4 учеников) и в тетрадях. При такой подаче материала очень высокий коэффициент усвоения. И самое главное, что у учащихся пропадает неуверенность. У них возникает чувство успешности, уверенности и самое главное — это желание освоить и остальные формулы.
Изучение формул замены суммы и разности на произведение и формул замены произведения на сумму и разность нужно вести параллельно.
Записать все формулы и начать их анализировать, опираясь на выше приведенные мнемонические правила .
COS+COS = 2 COS ( – ) \ 2•COS ( + ) \ 2
COS – COS = — 2 SIN( + ) \ 2•SIN ( – ) \ 2
SIN + SIN = 2 SIN( + ) \ 2• COS ( – ) \ 2
SIN — SIN = 2 SIN( — ) \2• COS ( + ) \ 2
Если внимательно присмотреться, то замечаем, что косинус «берет» функции одноименные и знак меняет: COS+COS и COS ( – ) \ 2 COS ( + ) \ 2 ; COS – COS и — 2 SIN( + ) \ 2• SIN ( – ) \ 2
причем, когда косинусы связаны знаком «+», т. е. «положительно», «хорошо», то он (косинус) берет своих « собратьев» — 2 COS ( – ) \ 2•COS ( + ) \ 2, а когда косинусы связаны знаком « — », т.е. «отрицательно», «плохо», то косинус берет функции одноименные, но не «собратьев», «подкрепляя» коэффициентом «-2».
Для синуса наше правило тоже сохраняется: он (синус) берет функции разноименные и знак не меняет: SIN + SIN = 2 SIN( + ) \ 2 и SIN — SIN = 2 SIN( — ) \2.
После таких рассуждений учащиеся вновь записывают и на доске и в тетрадях.
Для формул:
COSCOS = 0,5( COS ( – ) + COS ( + ) )
SINSIN == 0,5( COS ( – ) — COS ( + ) )
SINCOS =0,5( SIN ( – ) + COS ( + ) )
предложить учащимся самим применить рассмотренные мнемонические правила к этим формулам.
Ключ к решению тригонометрических задач
Школьница из Владимира успешно выступила во всероссийском конкурсе научно-исследовательских работ учащихся. Поездка на столь ответственные соревнования для ученицы гимназии №35 Елены Донской стала возможной благодаря поддержке депутата Госдумы Григория Викторовича Аникеева. Он уже много лет ведет в регионе системную работу по воспитанию и развитию детей и молодежи. Все подробности у Татьяны Даниловой.
Один из любимых школьных предметов Елены Донской — математика. Числа, уравнения, теоремы — тут ученица старших классов чувствует себя, как рыба в воде. Свою исследовательскую работу «Решение тригонометрических задач с помощью геометрических построений» на всероссийский конкурс Лена готовила три месяца, пройдя городскую и областную конференцию. В своём выступлении перед жюри — докторами наук ведущих вузов Москвы — Елена доказала, что сложные задачи из тригонометрии можно решать без длинных формул, а более лёгким способом, например, с помощью построения треугольника.
ЕЛЕНА ДОНСКАЯ, УЧЕНИЦА 10 КЛАССА ГИМНАЗИИ №35 г .ВЛАДИМИРА
Эта работа поможет некоторым людям, которые не понимают некоторые формулы по тригонометрии. Просто не могли их запомнить, не могли понять, откуда это берётся. Она всё-таки поможет взглянуть с другой стороны и с помощью геометрии, которая там используется, очень простые теоремы по геометрии, которые любой, наверное, человек может понять.
Доклад Елены Донской можно с уверенностью назвать методическим пособием по математике, как для педагогов, так и для учеников. В исследовательскую работу включён сборник задач. Он станет весомым подспорьем при подготовке к ЕГЭ, всевозможным олимпиадам по математике.
ИРИНА КУЛЕШОВА, ДИРЕКТОР ГИМНАЗИИ №35 Г.ВЛАДИМИРА
Мы, во-первых, очень рады, что у нас есть такие дети, которые хотят заниматься наукой, хотят заниматься исследовательской деятельностью. И есть педагоги, которые их поддерживают. + Педагоги видят результат своего труда, «глаз горит», работать хочется. Потому что мы видим, что дети проявляют себя всесторонне.
На финальное выступление в Москве старшеклассницу сопровождала её педагог по математике Елена Владимировна. Всего на всероссийский конкурс имени Дмитрия Ивановича Менделеева было подано свыше 3000 тысяч заявок, из которых было отобрано 500 лучших работ. Их авторы и боролись за призовые места. За 10 минут нужно было защитить свой проект и ответить на вопросы жюри. С чем Елена Донская блестяще справилась. Попадание в финал конкурса — большое достижение для региона. И очень важно, когда талантливые ребята чувствуют внимание со стороны общества. Елену Донскую поддержал депутат Григорий Аникеев. Вот уже второе десятилетие он ведет во Владимирской области работу по созданию условий для развития детей и молодежи: школьники получают персональные стипендии, участвуют в интеллектуальных турнирах и спортивных соревнованиях.
ЕЛЕНА ДУБОВА, УЧИТЕЛЬ МАТЕМАТИКИ ГИМНАЗИИ №35 Г.ВЛАДИМИРА
Григорий Викторович всегда поддерживает одарённую молодёжь, способствует их развитию и росту, за что ему огромное спасибо, потому, что позволяет нам дальше развиваться, и мне как педагогу, и детям.
Лауреат всероссийского конкурса — Елена Донская — на достигнутом точно не остановится. Она планирует и дальше совершенствовать свои знания, покорять новые вершины. Уже в мае старшеклассница отправится в лагерь «Артек», где встретится с такими же талантливыми детьми со всей России.
Татьяна Данилова, Егор Хрыпко
| За последние несколько страниц вы видели довольно много тригонометрических отождествлений. Для справки удобно иметь их краткое изложение. Эти тождества в основном относятся к одному углу, обозначенному θ , но есть некоторые, которые включают два угла, и для них два угла обозначены α и β . | |
Более важные идентичности.Вам не нужно знать все личности с головы до ног.Но вы должны это сделать. | |
| Определение отношений для тангенса, котангенса, секанса и косеканса в терминах синуса и косинуса. | |
| Формула Пифагора для синусов и косинусов. Это, наверное, самая важная триггерная идентичность. | |
| Идентификаторы, выражающие триггерные функции в терминах их дополнений. В этом нет ничего особенного.Каждая из шести триггерных функций равна своей совместной функции, оцениваемой под дополнительным углом. | |
| Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2 π , а тангенс и котангенс имеют период π . | |
| Обозначения для отрицательных углов. Синус, тангенс, котангенс и косеканс являются нечетными функциями, а косинус и секанс — четными функциями. | |
| Тождества Птолемея, формулы суммы и разности для синуса и косинуса. | |
| Формулы двойного угла для синуса и косинуса. Обратите внимание, что существует три формы формулы двойного угла для косинуса. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. | |
Менее важные идентичности.Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из вышеперечисленных, но иногда для этого требуется немного поработать. | |
| Формула Пифагора для касательных и секущих. Есть еще один для котангенсов и косекансов, но поскольку котангенсы и косекансы нужны редко, в нем нет необходимости. | |
| Идентификаторы, выражающие триггерные функции в терминах их дополнений. | |
| Формулы суммы, разности и двойного угла для тангенса. | |
| Формулы половинных углов. Для синуса и косинуса берут положительный или отрицательный квадратный корень в зависимости от квадранта угла θ /2. Например, если θ /2 — острый угол, тогда будет использоваться положительный корень. | |
Действительно неясные личности.Они здесь как раз для извращенности. Нет, не совсем. У них есть несколько приложений, но обычно это узкие приложения, и о них также можно забыть, пока они не понадобятся. | |
| Идентификаторы суммы продукта. Эта группа идентичностей позволяет вам преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов. | |
| Идентификационные данные продукта. Кроме того: как ни странно, эти идентификаторы продуктов использовались до того, как были изобретены логарифмы для выполнения умножения. Вот как можно использовать второй. Если вы хотите умножить x на y, используйте таблицу, чтобы найти угол α , косинус которого равен x , и угол β , косинус которого равен y . Найдите косинусы суммы α + β . а разность α — β . Усредните эти два косинуса.Вы получаете товар xy ! Три просмотра таблиц и вычисление суммы, разницы и среднего, а не одно умножение. Тихо Браге (1546–1601), среди прочих, использовал этот алгоритм, известный как простафаэрез . | |
| Формулы тройного угла. Вы можете легко восстановить их по формулам сложения и двойного угла. | |
| Еще формулы полууглов. Они описывают основные триггерные функции в терминах тангенса половины угла. Они используются в исчислении для определенного вида подстановки в интегралах, иногда называемой подстановкой Вейерштрасса t . | |
Тригонометрия
Тригонометрия (от греч. Тригонон «треугольник» + метрон «мера»)
Хотите изучить тригонометрию? Вот краткое изложение.
Чтобы узнать больше, перейдите по ссылкам или перейдите в Индекс тригонометрии
| Тригонометрия … это всего около треугольника. |
Тригонометрия помогает нам находить углы и расстояния и широко используется в науке, технике, видеоиграх и многом другом!
Прямоугольный треугольник
Наибольший интерес представляет прямоугольный треугольник. Прямой угол показан маленькой рамкой в углу:
Другой угол часто обозначается как θ, и тогда три стороны называются:
- Соседний : Соседний (рядом) угол θ
- Напротив : напротив угла θ
- , а самая длинная сторона — Гипотенуза
Почему прямоугольный треугольник?
Почему этот треугольник так важен?
Представьте, что мы можем измерять по длине и вверх, но хотим знать прямое расстояние и угол:
Тригонометрия может найти недостающий угол и расстояние.
Или, может быть, у нас есть расстояние и угол, и нам нужно «нарисовать точку» вдоль и вверх:
Подобные вопросы часто встречаются в инженерии, компьютерной анимации и т. Д.
И тригонометрия дает ответы!
Синус, косинус и тангенс
Основные функции в тригонометрии: Синус, косинус и тангенс
Это просто одна сторона прямоугольного треугольника, разделенная на другую.
Для любого угла « θ «:
(Синус, косинус и тангенс часто сокращаются до sin, cos и tan.)
Пример: Что такое синус 35 °?
Используя этот треугольник (длины до одного десятичного знака):
sin (35 °) = Напротив Гипотенуза = 2,8 4,9 = 0,57 …
Треугольник может быть больше, меньше или повернутым, но этот угол всегда будет иметь это соотношение .
В калькуляторах есть sin, cos и tan, чтобы помочь нам, поэтому давайте посмотрим, как ими пользоваться:
Пример: Насколько высокое дерево?
Мы не можем дотянуться до вершины дерева, поэтому мы уходим и измеряем угол (с помощью транспортира) и расстояние (с помощью лазера):
- Мы знаем Гипотенузу
- И мы хотим знать напротив
Синус — это отношение Противоположность / Гипотенуза :
грех (45 °) = напротив Гипотенуза
Возьмите калькулятор, введите «45», затем нажмите клавишу «sin»:
sin (45 °) = 0.7071 …
Что означает 0,7071 … ? Это отношение длин сторон, так что Противоположность примерно на 0,7071 в раз длиннее Гипотенузы.
Теперь мы можем поставить 0,7071 … вместо sin (45 °):
0,7071 … = Напротив Гипотенуза
И мы также знаем, что гипотенуза — 20 :
0,7071 … = Напротив 20
Чтобы решить, сначала умножьте обе части на 20:
20 × 0.7071 … = Напротив
Наконец:
Напротив = 14,14 м (с точностью до 2 знаков после запятой)
Когда вы наберетесь опыта, вы сможете сделать это быстро следующим образом:Пример: Насколько высокое дерево?
Начать с: sin (45 °) = напротив Гипотенуза
Мы знаем: 0,7071 … = напротив 20
Поменять местами: напротив 20 = 0.7071 …
Умножить обе стороны на 20 : Противоположное = 0,7071 … × 20
Вычислить: Противоположное = 14,14 (до 2 десятичных знаков)
Дерево 14,14 м высотой
Попробуйте Sin Cos and Tan
Поиграйте с этим некоторое время (перемещайте мышь) и ознакомьтесь со значениями синуса, косинуса и тангенса для разных углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °.
Также попробуйте 120 °, 135 °, 180 °, 240 °, 270 ° и т. Д. И обратите внимание, что позиции могут быть положительными или отрицательными, по правилам декартовых координат, поэтому синус, косинус и тангенс также изменяются между положительным и отрицательным .
Итак, тригонометрия — это тоже окружности !
Единичный круг
То, с чем вы только что играли, — это Unit Circle.
Это круг радиусом 1 с центром в 0.
Поскольку радиус равен 1, мы можем напрямую измерить синус, косинус и тангенс.
Здесь мы видим синусоидальную функцию, выполняемую единичной окружностью:
Примечание: вы можете увидеть красивые графики, состоящие из синуса, косинуса и тангенса.
Градусов и радианов
Углы могут быть в градусах или радианах. Вот несколько примеров:
| Уголок | Градусов | Радианы |
|---|---|---|
| Прямоугольный | 90 ° | π / 2 |
| __ Прямой угол | 180 ° | π |
| Полное вращение | 360 ° | 2π |
Повторяющийся узор
Поскольку угол равен вращению вокруг окружности , функции синуса, косинуса и тангенса повторяются один раз при каждом полном вращении (см. Амплитуда, Период, Фазовый сдвиг и Частота).
Когда мы хотим вычислить функцию для угла, превышающего полный оборот на 360 ° (2π радиан), мы вычитаем столько полных оборотов, сколько необходимо, чтобы вернуть его ниже 360 ° (2π радиан):
Пример: каков косинус 370 °?
370 ° больше 360 °, поэтому вычтем 360 °
370 ° — 360 ° = 10 °
cos (370 °) = cos (10 °) = 0,985 (до 3 знаков после запятой)
А когда угол меньше нуля, просто добавьте полные обороты.
Пример: какой синус у −3 радиан?
−3 меньше 0, поэтому добавим 2π радиан
−3 + 2π = −3 + 6,283 … = 3,283 … радиан
sin (−3) = sin (3,283 …) = −0,141 (до 3 знаков после запятой)
Решение треугольников
Тригонометрия также полезна для обычных треугольников, а не только для прямоугольных.
Это помогает нам решать треугольники. «Решение» означает поиск недостающих сторон и углов.
Мы также можем найти недостающие стороны.Общее правило:
Зная любые 3 стороны или углы, мы можем найти остальные 3
(за исключением случая с тремя углами)
См. Раздел «Решение треугольников» для более подробной информации.
Другие функции (котангенс, секанс, косеканс)
Подобно синусу, косинусу и касательности, есть еще три тригонометрические функции , которые выполняются делением одной стороны на другую:
Косекансная функция: | csc ( θ ) = Гипотенуза / Напротив |
Секущая функция: | сек ( θ ) = Гипотенуза / Соседний |
Функция котангенса: | детская кроватка ( θ ) = рядом / напротив |
Тригонометрические и треугольные идентичности
И по мере того, как вы станете лучше разбираться в тригонометрии, вы сможете выучить эти:
Станьте экспертом в области треугольников (и кругов)!
тригонометрия | Определение, формулы, соотношения и тождества
Слово тригонометрия происходит от греческих слов trigonon («треугольник») и metron («измерять»).Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений недостающих частей треугольника (или любой формы, которую можно разрезать на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина замкнутого угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая в основном исследует качественные отношения.Конечно, это различие не всегда является абсолютным: например, теорема Пифагора представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своей первоначальной форме тригонометрия в целом была порождением геометрии; только в 16 веке эти два направления стали отдельными разделами математики.
Древний Египет и Средиземноморский мир
Несколько древних цивилизаций, в частности египетская, вавилонская, индуистская и китайская, обладали значительными знаниями практической геометрии, включая некоторые концепции, которые были прелюдией к тригонометрии.Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 годом до н. Э., Содержит пять задач, касающихся секед . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для огромных строительных проектов, таких как пирамиды. Например, в задаче 56 задается вопрос: «Если пирамида имеет высоту 250 локтей, а длина стороны ее основания — 360 локтей, то какой у нее секед ?» Решение дается как 5 1 / 25 ладоней на локоть, и, поскольку один локоть равен 7 ладоням, эта фракция эквивалентна чистому соотношению 18 / 25 .На самом деле это отношение «бега к подъему» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне имели хоть какое-то представление о числовых отношениях в треугольнике, своего рода «прото-тригонометрии».
Египетский секедЕгиптяне определили секед как отношение пробега к подъему, что является обратной величиной современного определения наклона.
Британская энциклопедия, Inc. Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасТригонометрия в современном понимании началась с греков. Гиппарх ( ок. 190–120 до н. Э.) Был первым, кто построил таблицу значений тригонометрической функции. Он считал каждый треугольник — плоский или сферический — вписанным в круг, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником A B C на рисунке).Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который его образует, или, что то же самое, длину хорды как функцию соответствующей ширины дуги. Это стало главной задачей тригонометрии на следующие несколько столетий. Как астроном, Гиппарх в основном интересовался сферическими треугольниками, такими как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии.Во времена Гиппарха эти формулы были выражены в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их соединяют; современные символы для тригонометрических функций не были введены до 17 века.
треугольник, вписанный в кругЭтот рисунок иллюстрирует взаимосвязь между центральным углом θ (углом, образованным двумя радиусами в круге) и его хордой A B (равной одной стороне вписанного треугольника).
Encyclopædia Britannica, Inc.Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения
Теория Птолемея о солнечной системе.
Encyclopædia Britannica, Inc. См. Все видео к этой статьеПервой крупной древней работой по тригонометрии, которая дошла до Европы нетронутой после Средневековья, была Almagest Птолемея ( c. 100–170 гг. Н. Э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но о нем мало что известно.Хотя Птолемей написал работы по математике, географии и оптике, он в основном известен благодаря Альмагест , сборнику из 13 книг по астрономии, который стал основой для картины мира человечества до тех пор, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея. в середине 16 века. Чтобы создать эту картину мира, сутью которой была неподвижная Земля, вокруг которой Солнце, Луна и пять известных планет движутся по круговым орбитам, Птолемею пришлось использовать элементарную тригонометрию.Главы 10 и 11 первой книги Альмагест посвящены построению таблицы хорд, в которой длина хорды в окружности дается как функция от центрального угла, который ее образует, для углов в диапазоне от От 0 ° до 180 ° с интервалом в половину градуса. По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину вытянутой хорды c , чтобы получить c = 2 r sin А / 2 .Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса r = 60 единиц, так что c = 120 sin A / 2 . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin A / 2 и, следовательно, (путем удвоения дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические измерения мира и уточнил модель движения небесных тел Гиппарха.
построение таблицы хордОбозначив на рисунке центральный угол A , радиусы r и хорду c , можно показать, что c = 2 r sin ( A /2). Следовательно, таблица значений хорд в круге фиксированного радиуса также является таблицей значений синуса углов (путем удвоения дуги).
Encyclopædia Britannica, Inc.Тригонометрические функции и единичная окружность
Радианы
Радианы — это еще один способ измерения углов, и величина угла может быть преобразована между градусами и радианами.\ circ} {\ pi}} [/ латекс].
Ключевые термины
- дуга : Непрерывная часть окружности круга.
- окружность : длина линии, ограничивающей круг.
- радиан : Стандартная единица измерения углов в математике. Мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Введение в радианы
Напомним, что деление круга на 360 частей дает измерение в градусах. Это произвольное измерение, и мы можем выбрать другие способы разделить круг.Чтобы найти другую единицу, представьте себе процесс рисования круга. Представьте, что вы останавливаетесь до того, как круг замкнется. Нарисованная вами часть называется дугой. Дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется окружностью этого круга.
Окружность круга
[латекс] C = 2 \ pi r [/ латекс]
Если мы разделим обе части этого уравнения на [латекс] r [/ латекс], мы получим отношение длины окружности, которое всегда равно [латексу] 2 \ pi [/ латексу] к радиусу, независимо от длины радиус.Таким образом, длина окружности любого круга равна [латексу] 2 \ пи \ приблизительно в 6,28 [/ латексу] раз больше длины радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных длин струны и чуть больше четверти седьмой, как показано на диаграмме. ниже.
Длина окружности по сравнению с радиусом : Длина окружности чуть более чем в 6 раз превышает длину радиуса.
Это подводит нас к нашей новой угловой мере. Радиан — это стандартная единица измерения углов в математике. Один радиан — это мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Один радиан: Угол [латекс] t [/ латекс] выметает величину в один радиан. Обратите внимание, что длина перехваченной дуги равна длине радиуса круга.
Поскольку общая длина окружности равна [латексу] 2 \ pi [/ latex], умноженному на радиус, полный круговой поворот составляет [латекс] 2 \ pi [/ латекс] радиан.\ circ [/ латекс].
Обратите внимание, что когда угол описывается без конкретной единицы измерения, он относится к радианам. Например, величина угла 3 означает 3 радиана. Фактически, радиан безразмерен, так как это частное от длины (окружности), деленной на длину (радиус), а единицы длины сокращаются. Иногда вы можете увидеть радианы, представленные символом [latex] \ text {rad} [/ latex].
Сравнение радианов с градусами
Поскольку теперь мы знаем, что полный диапазон круга может быть представлен либо в 360 градусах, либо в [латексных] 2 \ пи [/ латексных] радианах, мы можем заключить следующее:
[латекс] \ displaystyle {\ begin {align} 2 \ pi \ text {радианы} & = 360 ^ {\ circ} \\ 1 \ text {radian} & = \ frac {360 ^ {\ circ}} {2 \ pi} \\ 1 \ text {radian} & = \ frac {180 ^ {\ circ}} {\ pi} \ end {align}} [/ latex]
Как указано, один радиан равен [latex] \ displaystyle {\ frac {180 ^ {\ circ}} {\ pi}} [/ latex] градусам или чуть меньше 57. {\ circ}} [/ latex].
Измерение угла в радианах
Длина дуги [латекс] s [/ латекс] — это длина кривой вдоль дуги. Так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, образованная любым заданным углом, также имеет постоянную связь с радиусом, независимо от длины радиуса.
Это отношение, называемое радианной мерой, одинаково независимо от радиуса круга — оно зависит только от угла. Это свойство позволяет нам определять меру любого угла как отношение длины дуги [latex] s [/ latex] к радиусу [latex] r [/ latex].
[латекс] \ displaystyle {\ begin {align} s & = r \ theta \\ \ theta & = \ frac {s} {r} \ end {align}} [/ latex]
Измерительные радианы: (a) под углом 1 радиан; длина дуги равна радиусу [латекс] r [/ латекс]. (b) Угол в 2 радиана имеет длину дуги [латекс] s = 2r [/ латекс]. (c) Полный оборот составляет [латекс] 2 \ pi [/ латекс], или около 6,28 радиана.
Пример
Какова мера данного угла в радианах, если длина его дуги равна [латекс] 4 \ pi [/ latex], а радиус — [латекс] [/ латекс] 12?
Подставьте значения [latex] s = 4 \ pi [/ latex] и [latex] r = 12 [/ latex] в формулу угла:
[латекс] \ displaystyle {\ begin {align} \ theta & = \ frac {s} {r} \\ & = \ frac {4 \ pi} {12} \\ & = \ frac {\ pi} {3 } \\ & = \ frac {1} {3} \ pi \ end {align}} [/ latex]
Угол имеет размер [latex] \ displaystyle {\ frac {1} {3} \ pi} [/ latex] радиан.
Определение тригонометрических функций на единичной окружности
Определение точек на единичной окружности позволяет применять тригонометрические функции к любому углу.
Цели обучения
Используйте прямоугольные треугольники, нарисованные в единичной окружности, чтобы определить тригонометрические функции для любого угла
Основные выводы
Ключевые моменты
- Координаты [latex] x [/ latex] — и [latex] y [/ latex] в точке единичной окружности, заданной углом [latex] t [/ latex], определяются функциями [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex].{\ circ} [/ латекс].
- Единичный круг демонстрирует периодичность тригонометрических функций, показывая, что они приводят к повторяющемуся набору значений через равные промежутки времени.
Ключевые термины
- периодичность : качество функции с повторяющимся набором значений через равные промежутки времени.
- единичная окружность : окружность с центром в начале координат и радиусом 1.
- квадрантов : Четыре четверти координатной плоскости, образованные осями [latex] x [/ latex] — и [latex] y [/ latex].
Тригонометрические функции и единичная окружность
Мы уже определили тригонометрические функции в терминах прямоугольных треугольников. В этом разделе мы переопределим их в терминах единичной окружности. Напомним, что единичный круг — это круг с центром в начале координат и радиусом 1. Угол [латекс] t [/ латекс] (в радианах) образует дугу длиной [латекс] s [/ латекс].
Оси x- и y- делят координатную плоскость (и единичную окружность, поскольку она центрирована в начале координат) на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление, в котором развернется положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [latex] t [/ latex] мы можем обозначить пересечение его стороны и единичного круга его координатами, [latex] (x, y) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f (t) = \ cos t [/ latex] и [latex] f (t). = \ sin t [/ latex] соответственно. Это означает:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ y & = \ sin t \ end {align}} [/ latex]
Эти координаты показаны на диаграмме единичного круга.
Единичный круг: Координаты точки на единичной окружности, центральный угол которой составляет [латекс] t [/ латекс] радиан.
Обратите внимание, что значения [latex] x [/ latex] и [latex] y [/ latex] задаются длинами двух сторон треугольника, окрашенных в красный цвет. Это прямоугольный треугольник, и вы можете видеть, как длины этих двух сторон (и значения [latex] x [/ latex] и [latex] y [/ latex]) задаются тригонометрическими функциями [latex] t [/латекс].
В качестве примера того, как это применимо, рассмотрим диаграмму, показывающую точку с координатами [latex] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] по единичной окружности.
Точка на единичном круге: точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] на единичном круге. .
Мы знаем, что для любой точки единичного круга координата [latex] x [/ latex] равна [latex] \ cos t [/ latex], а координата [latex] y [/ latex] — [latex] ] \ sin t [/ латекс]. Применяя это, мы можем определить, что [latex] \ displaystyle {\ cos t = — \ frac {\ sqrt2} {2}} [/ latex] и [latex] \ displaystyle {\ sin t = — \ frac {\ sqrt2} {2}} [/ латекс] для угла [латекс] t [/ латекс] на схеме.
Напомним, что [латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]. Применяя эту формулу, мы можем найти тангенс любого угла, обозначенного единичной окружностью. Для угла [латекс] t [/ латекс], указанного на диаграмме единичного круга, показывающего точку [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2 } \ right)} [/ latex], касательная:
[латекс] \ displaystyle {\ begin {align} \ tan t & = \ frac {\ sin t} {\ cos t} \\ & = \ frac {- \ frac {\ sqrt2} {2}} {- \ гидроразрыв {\ sqrt2} {2}} \\ & = 1 \ end {align}} [/ latex]
Ранее мы обсуждали тригонометрические функции в применении к прямоугольным треугольникам.{\ circ} [/ латекс].
Дальнейшее рассмотрение единичной окружности
Координаты определенных точек на единичной окружности и мера каждого угла в радианах и градусах показаны на диаграмме координат единичной окружности. Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.
Координаты единичной окружности : Единичная окружность, показывающая координаты и угловые размеры определенных точек.
Мы можем найти координаты любой точки единичной окружности.Учитывая любой угол [латекс] t [/ латекс], мы можем найти координату [latex] x [/ latex] или [latex] y [/ latex] в этой точке, используя [latex] x = \ text {cos} t [/ latex] и [latex] y = \ text {sin} t [/ latex].
Единичный круг демонстрирует периодичность тригонометрических функций. Периодичность относится к способу, которым тригонометрические функции приводят к повторяющемуся набору значений через равные промежутки времени. Взгляните на [latex] x [/ latex] -значения координат в единичном круге выше для значений [latex] t [/ latex] от [latex] 0 [/ latex] до [latex] 2 {\ pi} [/ latex]:
[латекс] {1, \ frac {\ sqrt {3}} {2}, \ frac {\ sqrt {2}} {2}, \ frac {1} {2}, 0, — \ frac {1} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {\ sqrt {3}} {2}, -1, — \ frac {\ sqrt {3}} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {1} {2}, 0, \ frac {1} {2}, \ frac {\ sqrt {2}} {2}, \ frac { \ sqrt {3}} {2}, 1} [/ латекс]
Мы можем определить закономерность в этих числах, которые колеблются между [латекс] -1 [/ латекс] и [латекс] 1 [/ латекс].Обратите внимание, что этот шаблон будет повторяться для более высоких значений [latex] t [/ latex]. Напомним, что эти значения [latex] x [/ latex] соответствуют [latex] \ cos t [/ latex]. Это показатель периодичности функции косинуса.
Пример
Решите [латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)}} [/ latex].
Похоже, это будет сложно решить. Однако обратите внимание, что диаграмма единичного круга показывает координаты в [latex] \ displaystyle {t = \ frac {7 \ pi} {6}} [/ latex].Поскольку координата [latex] y [/ latex] соответствует [latex] \ sin t [/ latex], мы можем идентифицировать, что
[латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)} = — \ frac {1} {2}} [/ latex]
Специальные уголки
Единичный круг и набор правил можно использовать для вызова значений тригонометрических функций специальных углов.
Цели обучения
Объясните, как свойства синуса, косинуса и тангенса и их знаки в каждом квадранте дают свои значения для каждого из специальных углов
Основные выводы
Ключевые моменты
- Тригонометрические функции для углов в единичной окружности можно запомнить и вызвать с помощью набора правил.
- Знак тригонометрической функции зависит от квадранта, в который попадает угол, и мнемоническая фраза «Умный класс триггера» используется для определения того, какие функции в каком квадранте положительны.
- Базовые углы в квадранте I используются для определения значения любого угла в квадрантах II, III или IV. Базовый угол образует тот же угол с осью [latex] x [/ latex], что и рассматриваемый угол.
- В единичную окружность включаются только функции синуса и косинуса для особых углов.Однако, поскольку тангенс получается из синуса и косинуса, его можно вычислить для любого из специальных углов.
Ключевые термины
- специальный угол : угол, кратный 30 или 45 градусам; тригонометрические функции легко записываются под этими углами.
Тригонометрические функции специальных углов
Напомним, что определенные углы и их координаты, которые соответствуют [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex] для данного угла [latex] t [/ latex], можно определить по единичному кругу.{\ circ} \ right)} & = 1 \\ \ end {align}} [/ latex]
Выражения для косинусных функций этих специальных углов также просты.
Обратите внимание, что, хотя только синус и косинус определяются непосредственно единичной окружностью, касательную можно определить как частное, включающее эти два:
[латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]
Касательные функции также имеют простые выражения для каждого из специальных углов.
Мы можем наблюдать эту тенденцию на примере.{\ circ} \ right)}} \\ & = \ frac {\ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \\ & = \ frac {\ sqrt {3 }} {2} \ cdot \ frac {2} {1} \\ & = \ sqrt {3} \ end {align}} [/ latex]
Запоминание тригонометрических функций
Понимание единичной окружности и способность быстро решать тригонометрические функции для определенных углов очень полезно в области математики. Применение правил и ярлыков, связанных с единичным кругом, позволяет быстро решать тригонометрические функции. Ниже приведены некоторые правила, которые помогут вам быстро решить такие проблемы.
Признаки тригонометрических функций
Знак тригонометрической функции зависит от квадранта, в который попадает угол. Чтобы помочь запомнить, какие из тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который является «А», все тригонометрических функций положительны.В квадранте II, «Умный», только синус является положительным. В квадранте III «Триггер» только , касательная положительна. Наконец, в квадранте IV «Класс» только , косинус положительный.
Правила знаков для тригонометрических функций: Каждая тригонометрическая функция перечислена в тех квадрантах, в которых она положительна.
Определение значений с использованием опорных углов
Внимательно посмотрите на единичный круг и обратите внимание, что [latex] \ sin t [/ latex] и [latex] \ cos t [/ latex] принимают определенные значения, поскольку они колеблются между [latex] -1 [/ latex] и [латекс] 1 [/ латекс]. {\ circ} [/ латекс].
Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса является координатой [latex] y [/ latex] на единичной окружности, другой угол с таким же синусом будет иметь такое же значение [latex] y [/ latex], но будет иметь противоположное значение [latex] x [/ latex] -значение. Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол.Угол с таким же косинусом будет иметь одно и то же значение [latex] x [/ latex], но будет иметь противоположное значение [latex] y [/ latex]. Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на схемах ниже, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны. Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ Displaystyle {\ begin {align} \ sin t = \ sin \ alpha \ quad & \ text {and} \ quad \ cos t = — \ cos \ alpha \\ \ sin t = — \ sin \ beta \ quad & \ text {and} \ quad \ cos t = \ cos \ beta \ end {align}} [/ latex]
Контрольные углы: На левом рисунке [латекс] t [/ latex] является контрольным углом для [латекс] \ альфа [/ латекс].{\ circ} [/ latex] или [latex] 0 [/ latex] и [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex] радиан. Для любого угла в квадранте II, III или IV существует опорный угол в квадранте I.
Контрольные углы в каждом квадранте: Для любого угла в квадрантах II, III или IV существует контрольный угол в квадранте I.
Таким образом, чтобы вызвать любой синус или косинус особого угла, вам необходимо определить его угол с осью [latex] x [/ latex], чтобы сравнить его с опорным углом.{\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]
Синус и косинус как функции
Функции синуса и косинуса можно изобразить, используя значения из единичной окружности, и на обоих графиках можно наблюдать определенные характеристики.
Цели обучения
Опишите характеристики графиков синуса и косинуса
Основные выводы
Ключевые моменты
- Как синусоидальную функцию [латекс] (y = \ sin x) [/ latex], так и косинусную функцию [латекс] (y = \ cos x) [/ latex] можно изобразить, нанеся точки, полученные из единичной окружности, с каждая координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] представляет собой соответствующее значение функции под этим углом.
- Синус и косинус — периодические функции с периодом [латекс] 2 \ пи [/ латекс].
- И синус, и косинус имеют домен [latex] (- \ infty, \ infty) [/ latex] и диапазон [latex] [- 1, 1] [/ latex].
- График [latex] y = \ sin x [/ latex] симметричен относительно начала координат, потому что это нечетная функция, в то время как график [latex] y = \ cos x [/ latex] симметричен относительно [latex ] y [/ latex] -axis, потому что это четная функция.
Ключевые термины
- период : интервал, содержащий значения, которые повторяются в функции.
- четная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = f (x) [/ latex], с симметрией относительно оси [латекс] y [/ латекс].
- нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , с симметрией относительно начала координат.
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], повторяющихся через равные промежутки времени.
Графические функции синуса и косинуса
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами [latex] x [/ latex] и [latex] y [/ latex] точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции [latex] y = \ sin x [/ latex]. Мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения для функции синуса на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ sin х [/ латекс]:
[латекс] \ displaystyle {(0, 0) \ quad (\ frac {\ pi} {6}, \ frac {1} {2}) \ quad (\ frac {\ pi} {4}, \ frac { \ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {2}, 1 ) \\ (\ frac {2 \ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {3 \ pi} {4}, \ frac {\ sqrt {2} } {2}) \ quad (\ frac {5 \ pi} {6}, \ frac {1} {2}) \ quad (\ pi, 0)} [/ latex]
Построение точек из таблицы и продолжение по оси [latex] x [/ latex] дает форму синусоидальной функции.
График синусоидальной функции: График точек с координатами [latex] x [/ latex], являющимися углами в радианах, и координатами [latex] y [/ latex], являющимися функцией [latex] \ sin x [/ latex] .
Обратите внимание, что значения синуса положительны между [latex] 0 [/ latex] и [latex] \ pi [/ latex], которые соответствуют значениям синусоидальной функции в квадрантах I и II на единичной окружности, и синусоидальной значения отрицательны между [латекс] \ пи [/ латекс] и [латекс] 2 \ пи [/ латекс], которые соответствуют значениям синусоидальной функции в квадрантах III и IV на единичной окружности.
Построение значений синусоидальной функции: Точки на кривой [латекс] y = \ sin x [/ latex] соответствуют значениям синусоидальной функции на единичной окружности.
Теперь давайте аналогичным образом посмотрим на функцию косинуса, [latex] f (x) = \ sin x [/ latex]. Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]:
[латекс] \ displaystyle {(0, 1) \ quad (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {4} , \ frac {\ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {1} {2}) \ quad (\ frac {\ pi} {2}, 0 ) \\ (\ frac {2 \ pi} {3}, — \ frac {1} {2}) \ quad (\ frac {3 \ pi} {4}, — \ frac {\ sqrt {2}} { 2}) \ quad (\ frac {5 \ pi} {6}, — \ frac {\ sqrt {3}} {2}) \ quad (\ pi, -1)} [/ latex]
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса.
График функции косинуса: Точки на кривой [latex] y = \ cos x [/ latex] соответствуют значениям функции косинуса на единичной окружности.
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичном круге, становится ясно, что диапазон обеих функций должен быть интервалом [latex] \ left [-1, 1 \ right] [/ latex].
Определение периодических функций
На графиках для функций синуса и косинуса форма графика повторяется после [latex] 2 \ pi [/ latex], что означает, что функции являются периодическими с периодом [latex] 2 \ pi [/ latex].Периодическая функция — это функция с повторяющимся набором значений через равные промежутки времени. В частности, это функция, для которой определенный горизонтальный сдвиг, [латекс] P [/ латекс], приводит к функции, равной исходной функции:
[латекс] f (x + P) = f (x) [/ латекс]
для всех значений [latex] x [/ latex] в домене [latex] f [/ latex]. Когда это происходит, мы называем наименьший такой сдвиг по горизонтали с [latex] P> 0 [/ latex] периодом функции. На приведенной ниже диаграмме показаны несколько периодов функций синуса и косинуса.
Периоды функций синуса и косинуса: Функции синуса и косинуса являются периодическими, что означает, что определенный горизонтальный сдвиг, [latex] P [/ latex], приводит к функции, равной исходной функции: [latex] f (x + P) = f (x) [/ латекс].
Четные и нечетные функции
Еще раз взглянув на функции синуса и косинуса в домене с центром на оси [latex] y [/ latex], можно выявить симметрии. Как мы можем видеть на графике синусоидальной функции, она симметрична относительно начала координат, что указывает на то, что это нечетная функция.На всем протяжении графика любые две точки с противоположными значениями [latex] x [/ latex] также имеют противоположные значения [latex] y [/ latex]. Это характерно для нечетной функции: два входа, которые являются противоположными, имеют выходы, которые также являются противоположными. Другими словами, если [латекс] \ sin (-x) = — \ sin x [/ latex].
Нечетная симметрия синусоидальной функции: Синусоидальная функция нечетная, что означает, что она симметрична относительно начала координат.
График функции косинуса показывает, что он симметричен относительно оси y .Это указывает на то, что это четная функция. Для четных функций любые две точки с противоположными значениями [latex] x [/ latex] имеют одинаковое значение функции. Другими словами, [латекс] \ cos (-x) = \ cos x [/ latex]. Мы можем видеть из графика, что это правда, сравнивая значения [latex] y [/ latex] графика с любыми противоположными значениями [latex] x [/ latex].
Четная симметрия функции косинуса: Функция косинуса четная, что означает, что она симметрична относительно оси [latex] y [/ latex].
Касательная как функция
Характеристики касательной функции можно увидеть на ее графике.
Цели обучения
Опишите характеристики графика касательной функции
Основные выводы
Ключевые моменты
- Функция касательной не определена при любом значении [latex] x [/ latex], где [latex] \ cos x = 0 [/ latex], и ее график имеет вертикальные асимптоты при этих значениях [latex] x [/ latex] .
- Касательная — периодическая функция с периодом [латекс] \ пи [/ латекс].
- График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией.
Ключевые термины
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex] с набором значений, повторяющихся через равные промежутки времени.
- период : интервал, содержащий минимальный набор значений, которые повторяются в периодической функции.
- нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , и есть симметрия относительно начала координат.
- вертикальная асимптота : прямая линия, параллельная оси [латекс] y [/ латекс], к которой кривая приближается произвольно близко, когда кривая уходит в бесконечность.
Построение касательной функции
Касательную функцию можно построить графиком путем нанесения точек [latex] \ left (x, f (x) \ right) [/ latex]. Форму функции можно создать, найдя значения тангенса под определенными углами. Однако невозможно найти касательные функции для этих особых углов с единичной окружностью.Мы применяем формулу [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], чтобы определить касательную для каждого значения.
Мы можем проанализировать графическое поведение касательной функции, посмотрев на значения некоторых специальных углов. Рассмотрим точки ниже, для которых координаты [latex] x [/ latex] представляют собой углы в радианах, а координаты [latex] y [/ latex] — [latex] \ tan x [/ latex]:
[латекс] \ displaystyle {(- \ frac {\ pi} {2}, \ text {undefined}) \ quad (- \ frac {\ pi} {3}, — \ sqrt {3}) \ quad (- \ frac {\ pi} {4}, -1) \ quad (- \ frac {\ pi} {6}, — \ frac {\ sqrt {3}} {3}) \ quad (0, 0) \\ (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {3}) \ quad (\ frac {\ pi} {4}, 1) \ quad (\ frac {\ pi} {3 }, \ sqrt {3}) \ quad (\ frac {\ pi} {2}, \ text {undefined})} [/ latex]
Обратите внимание, что [latex] \ tan x [/ latex] не определено в [latex] \ displaystyle {x = — \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ латекс].Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются по мере того, как [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы видим, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.
Напомним, что существует несколько значений [latex] x [/ latex], которые могут дать [latex] \ cos x = 0 [/ latex]. В любой такой точке [latex] \ tan x [/ latex] не определено, потому что [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex]. При значениях, при которых функция касания не определена, на ее графике наблюдаются разрывы. При этих значениях график касательной имеет вертикальные асимптоты.
График функции касательной: функция касательной имеет вертикальные асимптоты в [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ пи} {2}} [/ латекс].
Характеристики графика касательной функции
Как и функции синуса и косинуса, тангенс является периодической функцией. Это означает, что его значения повторяются через равные промежутки времени. Период касательной функции равен [latex] \ pi [/ latex], потому что график повторяется на [latex] x [/ latex] -осных интервалах [latex] k \ pi [/ latex], где [latex] k [/ latex] — это константа. На графике функции касательной на интервале [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex] к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex], мы можем увидеть поведение графика за один полный цикл функции.Если мы посмотрим на
любой больший интервал, мы увидим, что характеристики графика повторяются.
График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией. Другими словами, [latex] \ text {tan} (- x) = — \ text {tan} x [/ latex] для любого значения [latex] x [/ latex]. Любые две точки с противоположными значениями [latex] x [/ latex] производят противоположные значения [latex] y [/ latex]. Мы можем видеть, что это правда, рассматривая значения [latex] y [/ latex] графика при любых противоположных значениях [latex] x [/ latex].Рассмотрим [латекс] \ displaystyle {x = \ frac {\ pi} {3}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ pi} {3}} [/ latex]. Выше мы уже определили, что [латекс] \ displaystyle {\ tan (\ frac {\ pi} {3}) = \ sqrt {3}} [/ latex] и [latex] \ displaystyle {\ tan (- \ frac { \ pi} {3}) = — \ sqrt {3}} [/ latex].
Секанс и тригонометрические функции
Тригонометрические функции имеют обратные величины, которые можно вычислить с помощью единичной окружности.
Цели обучения
Вычислить значения тригонометрических функций, которые являются обратными синусу, косинусу и тангенсу
Основные выводы
Ключевые моменты
- Секущая функция обратна функции косинуса [latex] \ displaystyle {\ left (\ sec x = \ frac {1} {\ cos x} \ right)} [/ latex].Его можно найти для угла [латекс] t [/ latex], используя координату [latex] x [/ latex] связанной точки на единичной окружности: [latex] \ displaystyle {\ sec t = \ frac { 1} {x}} [/ латекс].
- Функция косеканса является обратной функцией синусоидальной функции [latex] \ displaystyle {\ left (\ csc x = \ frac {1} {\ sin x} \ right)} [/ latex]. Его можно найти для угла [латекс] t [/ latex], используя координату [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ csc t = \ frac { 1} {y}} [/ латекс].
- Функция котангенса является обратной функцией касательной [латекс] \ displaystyle {\ left (\ cot x = \ frac {1} {\ tan x} = \ frac {\ cos t} {\ sin t} \ right) }[/латекс]. Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].
Ключевые термины
- секанс : величина, обратная функции косинуса
- косеканс : функция, обратная синусоиде
- котангенс : величина, обратная тангенциальной функции
Введение в взаимные функции
Мы обсудили три тригонометрические функции: синус, косинус и тангенс.Каждая из этих функций имеет обратную функцию, которая определяется обратной величиной отношения исходной тригонометрической функции. Обратите внимание, что обратные функции отличаются от обратных функций. Обратные функции — это способ работы в обратном направлении или определения угла с учетом тригонометрического отношения; они предполагают работу с теми же соотношениями, что и исходная функция.
Три взаимные функции описаны ниже.
Секант
Секущая функция обратна функции косинуса и обозначается сокращенно как [латекс] \ сек [/ латекс].
Его можно описать как отношение длины гипотенузы к длине соседней стороны в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ sec x & = \ frac {1} {\ cos x} \\ \ sec x & = \ frac {\ text {hypotenuse}} {\ text {смежный}} \ end {align}} [/ latex]
Секанс легко вычислить со значениями в единичной окружности. Напомним, что для любой точки круга значение [latex] x [/ latex] дает [latex] \ cos t [/ latex] для соответствующего угла [latex] t [/ latex].Следовательно, секущая функция для этого угла равна
[латекс] \ displaystyle {\ sec t = \ frac {1} {x}} [/ latex]
Косеканс
Косекансная функция является обратной функцией синусоидальной функции и сокращенно обозначается как [latex] \ csc [/ latex]. Его можно описать как отношение длины гипотенузы к длине противоположной стороны треугольника.
[латекс] \ displaystyle {\ begin {align} \ csc x & = \ frac {1} {\ sin x} \\ \ csc x & = \ frac {\ text {hypotenuse}} {\ text {напротив}} \ end {align}} [/ latex]
Как и секанс, косеканс может быть вычислен со значениями в единичной окружности.Напомним, что для любой точки круга значение [latex] y [/ latex] дает [latex] \ sin t [/ latex]. Следовательно, функция косеканса для того же угла равна
[латекс] \ displaystyle {\ csc t = \ frac {1} {y}} [/ латекс]
Котангенс
Функция котангенса обратна функции тангенса и обозначается сокращенно как [latex] \ cot [/ latex]. Его можно описать как отношение длины соседней стороны к длине гипотенузы в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ cot x & = \ frac {1} {\ tan x} \\ \ cot x & = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align}} [/ latex]
Также обратите внимание, что поскольку [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], его обратная величина равна
[латекс] \ displaystyle {\ cot x = \ frac {\ cos x} {\ sin x}} [/ latex]
Котангенс также можно вычислить со значениями в единичной окружности.Применяя координаты [latex] x [/ latex] и [latex] y [/ latex], связанные с углом [latex] t [/ latex], получаем
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ \ cot t & = \ frac {x} {y} \ end {align}} [/ латекс]
Вычисление взаимных функций
Теперь мы распознаем шесть тригонометрических функций, которые можно вычислить, используя значения в единичном круге. Напомним, что мы использовали значения функций синуса и косинуса для вычисления функции тангенса.Мы будем следовать аналогичному процессу для обратных функций, ссылаясь на значения в единичном круге для наших расчетов.
Например, давайте найдем значение [latex] \ sec {\ left (\ frac {\ pi} {3} \ right)} [/ latex].
Применяя [latex] \ displaystyle {\ sec x = \ frac {1} {\ cos x}} [/ latex], мы можем переписать это как:
[латекс] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)} = \ frac {1} {\ cos {\ left ({\ frac {\ pi} {3}} \ right)}}} [/ латекс]
Из единичного круга мы знаем, что [латекс] \ displaystyle {\ cos {\ left ({\ frac {\ pi} {3}} \ right)} = \ frac {1} {2}} [/ latex] .Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]:
[латекс] \ displaystyle {\ begin {align} \ sec {\ left (\ frac {\ pi} {3} \ right)} & = \ frac {1} {\ frac {1} {2}} \\ & = 2 \ end {align}} [/ латекс]
Остальные взаимные функции могут быть решены аналогичным образом.
Пример
Используйте единичный круг, чтобы вычислить [латекс] \ sec t [/ latex], [latex] \ cot t [/ latex] и [latex] \ csc t [/ latex] в точке [latex] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex].
Точка на единичном круге: Точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex] , показанный в единичном круге.
Поскольку нам известны координаты [latex] (x, y) [/ latex] точки на единичной окружности, обозначенной углом [latex] t [/ latex], мы можем использовать эти координаты для поиска трех функций.
Напомним, что координата [latex] x [/ latex] дает значение для функции косинуса, а координата [latex] y [/ latex] дает значение для функции синуса.Другими словами:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ & = — \ frac {\ sqrt {3}} {2} \ end {align}} [/ latex]
и
[латекс] \ displaystyle {\ begin {align} y & = \ sin t \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Используя эту информацию, можно вычислить значения обратных функций под углом [латекс] t [/ латекс]:
[латекс] \ displaystyle {\ begin {align} \ sec t & = \ frac {1} {\ cos t} \\ & = \ frac {1} {x} \\ & = \ left (\ frac {1 } {- \ frac {\ sqrt {3}} {2}} \ right) \\ & = — \ frac {2} {\ sqrt {3}} \\ & = \ left (- \ frac {2} { \ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} \ right) \\ & = — \ frac {2 \ sqrt {3}} {3} \ end {align} } [/ латекс]
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ & = \ frac {x} {y} \\ & = \ left (\ frac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \ right) \\ & = \ left (- \ frac {\ sqrt {3}} {2} \ cdot \ frac {2} {1} \ right) \\ & = — \ sqrt {3} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} \ csc t & = \ frac {1} {\ sin t} \\ & = \ frac {1} {y} \\ & = \ left (\ frac {1 } {\ frac {1} {2}} \ right) \\ & = 2 \ end {align}} [/ latex]
Обратные тригонометрические функции
У каждой тригонометрической функции есть обратная функция, которую можно изобразить в виде графика. {- 1} x = y [/ latex].{-1} [/ латекс]
Введение в обратные тригонометрические функции
Обратные тригонометрические функции используются для нахождения углов треугольника, если нам заданы длины сторон. Обратные тригонометрические функции могут использоваться, чтобы определить, какой угол даст определенное значение синуса, косинуса или тангенса.
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной.{-1} (б) = а [/ латекс]. Однако функции синуса, косинуса и тангенса — это , а не взаимно однозначные функции. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область определения каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем домен для каждой функции, который включает число [latex] 0 [/ latex].
Функции синуса и косинуса в ограниченных областях: (a) Функция синуса, показанная в ограниченной области [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ справа] [/ латекс]; (b) Функция косинуса, показанная в ограниченной области [latex] \ left [0, \ pi \ right] [/ latex].
График функции синуса ограничен областью [latex] [- \ frac {\ pi} {2}, \ frac {\ pi} {2}] [/ latex] и графиком функции косинуса ограничено [латексом] [0, \ pi] [/ латексом]. График касательной функции ограничен [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Касательная функция в ограниченной области
Касательная функция, показанная в ограниченной области [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Эти варианты ограниченных доменов в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает взаимно однозначную функцию, которая является обратимой. Традиционный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он простирается от одной вертикальной асимптоты к другой вместо того, чтобы разбиваться на части асимптотой.{-1} x \ quad \ text {имеет домен} \ quad \ left (- \ infty, \ infty \ right) \ quad \ text {и диапазон} \ quad \ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right)} [/ latex]
Графики обратных тригонометрических функций
Функция синуса и функция обратного синуса (или арксинуса): функция арксинуса является отражением функции синуса относительно линии [latex] y = x [/ latex].
Чтобы найти область определения и диапазон обратных тригонометрических функций, мы меняем область определения и диапазон исходных функций.
Функция косинуса и функция обратного косинуса (или арккосинуса): Функция арккосинуса является отражением функции косинуса относительно линии [латекс] y = x [/ latex].
Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Функция тангенса и функция арктангенса (или арктангенса): Функция арктангенса является отражением функции касательной относительно линии [latex] y = x [/ latex].{-1} х = у [/ латекс].
36 триггерных идентификаторов, которые необходимо знать
Если вы посещаете уроки геометрии или тригонометрии, одна из тем, которые вы будете изучать, — это тригонометрические тождества. Существует множество триггерных идентификаторов, некоторые из которых вам необходимо знать, а другие вы будете использовать редко или никогда. В этом руководстве объясняются триггерные идентификаторы, которые вам следует запомнить, а также другие, о которых вы должны знать. Мы также объясняем, что такое триггерные идентификаторы и как вы можете проверить триггерные идентификаторы.
В математике «идентичность» — это уравнение, которое всегда верно, каждый раз. Тригонометрические тождества — это всегда истинные тригонометрические уравнения, которые часто используются для решения задач тригонометрии и геометрии и понимания различных математических свойств. Знание ключевых триггерных идентификаторов поможет вам запомнить и понять важные математические принципы и решить множество математических задач.
25 самых важных триггерных идентичностей
Ниже приведены шесть категорий триггерных тождеств, которые вы будете часто видеть. Каждый из них является идентификатором ключевого триггера и должен быть запомнен. Поначалу кажется, что это много, но как только вы начнете их изучать, вы увидите, что многие следуют шаблонам, которые облегчают их запоминание.
Основные личности
Эти идентификаторы определяют шесть триггерных функций. 2 $ ).2 (θ) $$
Совместные функции
Каждая из триггерных функций равна своей совместной функции, оцениваемой под дополнительным углом.
$$ sin (θ) = cos ({π / 2} — θ) $$
$$ cos (θ) = sin ({π / 2} — θ) $$
$$ tan (θ) = детская кроватка ({π / 2} — θ) $$
$$ детская кроватка (θ) = загар ({π / 2} — θ) $$
$$ csc (θ) = сек ({π / 2} — θ) $$
$$ сек (θ) = csc ({π / 2} — θ) $$
Идентификаторы с отрицательным углом
Синус, тангенс, котангенс и косеканс являются нечетными функциями (симметричными относительно начала координат).Косинус и секанс — четные функции (симметричны относительно оси y).
$$ sin (-θ) = -sin (θ) $$
$$ cos (-θ) = cos (θ) $$
$$ загар (-θ) = -тан (θ) $$
Тождества суммы и разности
Иногда их называют идентичностями Птолемея, поскольку он первый доказал их.
$$ sin (α + β) = sin (α) cos (β) + cos (α) sin (β) $$
$$ sin (α — β) = sin (α) cos (β) — cos (α) sin (β) $$
$$ cos (α + β) = cos (α) cos (β) — sin (α) sin (β) $$
$$ cos (α — β) = cos (α) cos (β) + sin (α) sin (β) $$
Двойные уголки
Вам нужно запомнить только одно из тождеств двойного угла для косинуса.2 (θ)} $$
Дополнительные идентификаторы триггеров
Эти три категории триггерных идентификаторов используются реже. Вы должны просмотреть их, чтобы убедиться, что вы их понимаете, но их обычно не нужно запоминать.
Полуугловые идентичности
Это инверсия тождеств с двойным углом.
$$ sin2 (θ) = {1/2} (1-cos (2θ)) $$
$$ cos2 (θ) = {1/2} (1+ cos (2θ)) $$
$$ tan2 (θ) = {1-cos (2θ)} / {1+ cos (2θ)} $$
Сумма идентичностей
Эти триггерные тождества позволяют вам преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов.
$$ sin (α) + sin (β) = 2sin ({α + β} / 2) cos ({α — β} / 2) $$
$$ sin (α) — sin (β) = 2cos ({α + β} / 2) sin ({α — β} / 2) $$
$$ cos (α) + cos (β) = 2cos ({α + β} / 2) cos ({α — β} / 2) $$
$$ cos (α) — cos (β) = -2sin ({α + β} / 2) sin ({α — β} / 2) $$
Обозначения продукта
Эта группа триггерных идентификаторов позволяет вам преобразовать произведение синусов или косинусов в произведение или разность синусов и косинусов.
$$ sin (α) cos (β) = {1/2} (sin (α + β) + sin (α — β)) $$
$$ cos (α) sin (β) = {1/2} (sin (α + β) — sin (α — β)) $$
$$ sin (α) sin (β) = {1/2} (cos (α — β) — cos (α + β)) $$
$$ cos (α) cos (β) = {1/2} (cos (α — β) + cos (α + β)) $$
Проверка тригонометрических идентичностей
После того, как вы изучите все ключевые триггерные идентификаторы в своем классе математики, следующим шагом будет их проверка. Проверка идентичности триггеров означает приравнивание двух сторон данного уравнения друг к другу, чтобы доказать, что оно истинно. Вы будете использовать триггерные идентификаторы, чтобы изменить одну или обе стороны уравнения, пока они не станут одинаковыми.
Для проверки идентичности триггеров может потребоваться множество различных математических методов, включая FOIL, распределение, подстановки и конъюгации. Для каждого уравнения потребуются разные методы, но есть несколько советов, которые следует помнить при проверке тригонометрических тождеств.
# 1: Начните с более жесткой стороны
Несмотря на то, что вы можете изначально захотеть сделать, мы рекомендуем начинать с той стороны уравнения, которая выглядит более запутанной или более сложной. Сложно выглядящие уравнения часто дают вам больше возможностей для опробования, чем более простые уравнения, поэтому начните с более сложной стороны, чтобы у вас было больше возможностей.
# 2: Помните, что вы можете менять обе стороны
Вам не нужно ограничиваться изменением только одной части уравнения. Если вы застряли на одной стороне, вы можете переключиться на другую сторону и также начать менять ее. Ни одна из сторон уравнения не должна совпадать с исходной; до тех пор, пока обе части уравнения оказываются идентичными, идентичность подтверждена.
# 3: Превратите все функции в синусы и косинусы
Большинство студентов, изучающих триггерные тождества, чувствуют себя наиболее комфортно с синусами и косинусами, потому что это триггерные функции, которые они видят чаще всего. Облегчите себе жизнь, преобразовав все функции в синусы и косинусы!
Пример 1
Проверить идентичность $ cos (θ) sec (θ) = 1 $
Давайте заменим секанс на косинус. Используя основные тождества, мы знаем, что $ sec (θ) = 1 / {cos (θ)} $. Это дает нам:
$$ cos (θ) (1 / {cos (θ)}) = 1 $$
Косинусы слева компенсируют друг друга, в результате чего получается $ 1 = 1 $.
Личность подтверждена!
Пример 2
Проверить тождество $ 1 — cos (2θ) = tan (θ) sin (2θ) $
Давайте начнем с левой стороны, так как с ней происходит еще кое-что.2 (θ) $$
Обе стороны идентичны, т. Е. Идентичность подтверждена!
Пример 3
Проверить идентичность $ sec (-θ) = sec (θ) $
Левая часть уравнения немного сложнее, поэтому давайте заменим секанс на синус или косинус. Из основных триггерных тождеств мы знаем, что $ sec (θ) = 1 / {cos (θ)} $, что означает, что $ sec (-θ) = 1 / {cos (-θ)} $. Замените левую часть:
$$ 1 / {cos (-θ)} = сек (θ) $$
Тождества с отрицательным углом говорят нам, что $ cos (-θ) = cos (θ) $, поэтому sub that:
$$ 1 / {cos (θ)} = сек (θ) $$
Опять же, мы знаем, что $ sec (θ) = 1 / {cos (θ)} $, поэтому получаем:
$$ сек (θ) = сек (θ) $$
Личность подтверждена!
Резюме: Решатель идентификаторов триггеров
Вам необходимо запомнить ключевые тригонометрические характеристики, чтобы хорошо учиться на уроках геометрии или тригонометрии. Хотя может показаться, что существует множество тригонометрических отождествлений, многие следуют схожему шаблону, и не все нужно запоминать.
При проверке идентификаторов триггеров помните следующие три совета:
- Начните с более сложной стороны
- Помните, что вы можете изменить обе стороны уравнения
- Превратите функции в синусы и косинусы
Что дальше?
Хотите знать, какие уроки математики выбрать в средней школе? Изучите лучшие уроки математики для старшеклассников, прочитав наше руководство!
Хотите знать, следует ли вам использовать исчисление AB или BC? В нашем руководстве описаны различия между двумя классами и объясняется, кто должен проходить каждый курс.
Заинтересованы в математических соревнованиях, таких как Международная математическая олимпиада ? Смотрите наше руководство по прохождению квалификационных тестов.
Тригонометрические функции
М. Борна
Зачем изучать тригонометрические функции …?
Триггерные функции очень важны в технических предметах, таких как наука, инженерия, архитектура и даже медицина. Вы будете сталкиваться с ними постоянно, так что их стоит хорошо изучить!
Геодезия — одно из многих приложений.Дорожники, строители мостов и те, кто ставит строения в нужное место, используют тригонометрию в своей повседневной работе.
Чтобы узнать о других приложениях и примерах тригонометрии в интерактивной математике, ознакомьтесь со многими вариантами использования тригонометрии. См. Также: Подсказки по математике — Тригонометрия.
В этой главе мы начнем с объяснения основных тригонометрических функций, используя градусы (°), а в более поздней части главы мы узнаем о радианах и о том, как они используются в тригонометрии.
Связанные разделы в «Интерактивной математике»
Графики тригонометрических функций, которые действительно помогают понять, что происходит в тригонометрии.
Аналитическая тригонометрия, которая включает формулы двойного угла, тригонометрические отношения суммы двух углов, тригонометрические уравнения и обратные тригонометрические уравнения.
Полярные координаты, которые работают примерно так же, как и темы в этой главе.
Производные трансцендентных функций, в котором показано, как различать функции sin, cos, tan, csc, sec и cot.
Интеграция с использованием тригонометрических форм, где мы видим, как наши знания тригонометрии могут упростить исчисление.
Линейный спектр в рядах Фурье, который представляет собой передовое приложение тригонометрии.
И, конечно же, не пропустите обзор использования тригонометрии.
В этой главе
1. Углы — строительные блоки тригонометрии. В градусах .
2. Синус, косинус, касательная и обратные дроби — эти дроби являются ключевыми для всех будущих исследований тригонометрии.
3. Значения тригонометрических функций — Почему sin 30 ° = 0,5?
4. Прямой треугольник и приложения — включает угол наклона ° n и угол возвышения ° .
5. Знаки тригонометрических функций — в этом нет ничего страшного, если вы помните, как мы определяем основные соотношения. Включает интерактивный документ , чтобы увидеть, как работают отношения углов, превышающих 90 градусов.
6. Тригонометрические функции под любым углом — не сдавайтесь в этом разделе!
7.Радианы — альтернатива градусам — и многое другое.
8. Приложения Radian Measure — включает длину дуги , площадь сектора , угловую скорость , игру и шкивы.
9. Радианы и тригонометрические соотношения — как работает тригонометрия, когда угол составляет радиан .
Эта глава начинается с некоторых напоминаний об углах.
7.4 Другие тригонометрические функции — алгебра и тригонометрия
Цели обучения
В этом разделе вы:
- Найдите точные значения тригонометрических функций секанса, косеканса, тангенса и котангенса чисел π3, π4, π3, π4 и π6.π6.
- Используйте базовые углы для вычисления секанса, тангенса и котангенса тригонометрических функций.
- Используйте свойства четных и нечетных тригонометрических функций.
- Признавайте и используйте фундаментальные идентичности.
- Оценивайте тригонометрические функции с помощью калькулятора.
Пандус для инвалидных колясок, соответствующий стандартам Закона об американцах с ограниченными возможностями, должен образовывать угол с землей, касательная которого равна 112112 или меньше, независимо от его длины.Касательная представляет собой отношение, поэтому это означает, что на каждый 1 дюйм подъема у рампы должен быть 12 дюймов пробега. Тригонометрические функции позволяют нам определять формы и пропорции объектов независимо от точных размеров. Мы уже определили функции синуса и косинуса угла. Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции.
Нахождение точных значений секанса, косеканса, тангенса и котангенса тригонометрических функций
Мы также можем определить остальные функции в терминах единичной окружности с точкой (x, y) (x, y), соответствующей углу t, t, как показано на рисунке 1. Как и в случае с синусом и косинусом, мы можно использовать координаты (x, y) (x, y), чтобы найти другие функции.
Рисунок 1
Первая функция, которую мы определим, — это касательная. Тангенс угла — это отношение значения y к значению x соответствующей точки на единичной окружности.На рисунке 1 тангенс угла tt равен yx, x ≠ 0.yx, x ≠ 0. Поскольку значение y равно синусу t, t, а значение x равно косинусу t, t, тангенс угла tt также можно определить как sintcost, cost cost 0. синткост, стоимость ≠ 0. Функция касательной обозначается как tan.tan. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили.
- Секущая функция обратна функции косинуса.На рисунке 1 секущая угла tt равна 1cost = 1x, x ≠ 0,1cost = 1x, x ≠ 0. Секущая функция сокращается до sec.sec.
- Функция котангенса обратна функции тангенса. На рисунке 1 котангенс угла tt равен costint = xy, y 0.costsint = xy, y ≠ 0. Функция котангенса сокращенно обозначается как cot.cot.
- Функция косеканса обратна функции синуса. На рисунке 1 косеканс угла tt равен 1sint = 1y, y ≠ 0,1sint = 1y, y ≠ 0. Функция косеканса сокращенно обозначается csc.csc.
Функции касания, секанса, косеканса и котангенса
Если tt — действительное число и (x, y) (x, y) — точка, в которой конечная сторона угла tt радиан пересекает единичный круг, то
tan t = yx, x ≠ 0sec t = 1x, x ≠ 0csc t = 1y, y ≠ 0cot t = xy, y ≠ 0tan t = yx, x ≠ 0sec t = 1x, x ≠ 0csc t = 1y, y ≠ 0cot t = xy, y ≠ 0Пример 1
Нахождение тригонометрических функций из точки единичной окружности
Точка (−32,12) (- 32,12) находится на единичной окружности, как показано на рисунке 2.Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott.
Рисунок 2
Решение
Поскольку нам известны координаты (x, y) (x, y) точки на единичной окружности, обозначенной углом t, t, мы можем использовать эти координаты для нахождения шести функций: sin t = y = 12cos t = x = −32tan t = yx = 12−32 = 12 (−23) = — 13 = −33sec t = 1x = 1−32 = −23 = −233csc t = 1y = 112 = 2cot t = xy = −3212 = −32 (21) = — 3sin t = y = 12cos t = x = −32tan t = yx = 12−32 = 12 (−23) = — 13 = −33sec t = 1x = 1−32 = −23 = −233csc t = 1y = 112 = 2cot t = xy = −3212 = −32 (21) = — 3
Попробуй # 1
Точка (22, −22) (22, −22) находится на единичной окружности, как показано на рисунке 3.Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott.
Рисунок 3
Пример 2
Нахождение тригонометрических функций угла
Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott. когда t = π6.t = π6.
Решение
Ранее мы использовали свойства равносторонних треугольников, чтобы продемонстрировать, что sinπ6 = 12sinπ6 = 12 и cosπ6 = 32.cosπ6 = 32. Мы можем использовать эти значения и определения тангенса, секанса, косеканса и котангенса как функций синуса и косинуса, чтобы найти остальные значения функции.
tanπ6 = sinπ6cosπ6 = 1232 = 13 = 33secπ6 = 1cosπ6 = 132 = 23 = 233cscπ6 = 1sinπ6 = 112 = 2cotπ6 = cosπ6sinπ6 = 3212 = 3tanπ6 = sinπ6cosπ6 = 1232 = 13 = 33secπ6 = 1cosπ6 = 132 = 23 = 233cπ6 = 1cosπ6 = 132 = 23 = 233c 2cotπ6 = cosπ6sinπ6 = 3212 = 3Попробуй # 2
Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott. когда t = π3.t = π3.
Поскольку мы знаем значения синуса и косинуса для общих углов первого квадранта, мы можем найти другие значения функций для этих углов, установив xx равным косинусу и yy равным синусу, а затем используя определения тангенса, секанс, косеканс и котангенс.Результаты представлены в таблице 1.
| Угол | 00 | π6, или 30 ° π6, или 30 ° | π4, или 45 ° π4, или 45 ° | π3, или 60 ° π3, или 60 ° | π2, или 90 ° π2, или 90 ° |
|---|---|---|---|---|---|
| Косинус | 1 | 3232 | 2222 | 1212 | 0 |
| Синус | 0 | 1212 | 2222 | 3232 | 1 |
| Касательная | 0 | 3333 | 1 | 33 | Неопределенный |
| Секант | 1 | 233233 | 22 | 2 | Неопределенный |
| Косеканс | Неопределенный | 2 | 22 | 233233 | 1 |
| Котангенс | Неопределенный | 33 | 1 | 3333 | 0 |
Таблица 1
Использование опорных углов для вычисления тангенса, секанса, косеканса и котангенса
Мы можем оценивать тригонометрические функции углов вне первого квадранта, используя опорные углы, как мы уже делали с функциями синуса и косинуса.Процедура такая же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке 4 показано, какие функции в каком квадранте положительны.
Чтобы запомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера.Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который представляет собой « A », ll из шести тригонометрических функций положительны. В квадранте II « S mart» только s ine и его обратная функция, косеканс, положительны. В квадранте III «установка T » только t angent и его обратная функция, котангенс, положительны.Наконец, в квадранте IV « C девушка» только c осин и его реципрокная функция, секанс, положительны.
Рис. 4 Каждая тригонометрическая функция перечислена в тех квадрантах, в которых она положительна.
Учитывая угол не в первом квадранте, используйте опорные углы, чтобы найти все шесть тригонометрических функций.
- Измерьте угол, образованный конечной стороной данного угла и горизонтальной осью. Это опорный угол.
- Оцените функцию под опорным углом.
- Обратите внимание на квадрант, в котором расположена конечная сторона исходного угла. Основываясь на квадранте, определите, будет ли выходной сигнал положительным или отрицательным.
Пример 3
Использование опорных углов для поиска тригонометрических функций
Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −5π6. − 5π6.
Решение
Угол между конечной стороной этого угла и осью x равен π6, π6, так что это опорный угол.Поскольку −5π6−5π6 находится в третьем квадранте, где и xx, и yy отрицательны, косинус, синус, секанс и косеканс будут отрицательными, а тангенс и котангенс будут положительными.
cos (−5π6) = — 32, sin (−5π6) = — 12, tan (−5π6) = 33, сек (−5π6) = — 233, csc (−5π6) = — 2, детская кроватка (−5π6) = 3cos (−5π6) = — 32, sin (−5π6) = — 12, tan (−5π6) = 33, sec (−5π6) = — 233, csc (−5π6) = — 2, детская кроватка (−5π6) = 3
Попробуй # 3
Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −7π4. − 7π4.
Использование четных и нечетных тригонометрических функций
Чтобы иметь возможность свободно использовать наши шесть тригонометрических функций с входными положительными и отрицательными углами, мы должны изучить, как каждая функция обрабатывает отрицательный вход.Как оказалось, в этом отношении между функциями есть важное различие.
Рассмотрим функцию f (x) = x2, f (x) = x2, показанную на рисунке 5. График функции симметричен относительно оси y . На всем протяжении кривой любые две точки с противоположными значениями x имеют одинаковое значение функции. Это соответствует результату расчета: (4) 2 = (- 4) 2, (- 5) 2 = (5) 2, (4) 2 = (- 4) 2, (- 5) 2 = (5) 2 , и так далее. Таким образом, f (x) = x2f (x) = x2 — четная функция, такая функция, что два противоположных входа имеют одинаковый выход.Это означает, что f (−x) = f (x) .f (−x) = f (x).
Рисунок 5 Функция f (x) = x2f (x) = x2 — четная функция.Теперь рассмотрим функцию f (x) = x3, f (x) = x3, показанную на рисунке 6. График несимметричен относительно оси y . На всем протяжении графика любые две точки с противоположными значениями x также имеют противоположные значения y . Итак, f (x) = x3f (x) = x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f (−x) = — f (x) .f (−x) = — f (x).
Рисунок 6 Функция f (x) = x3f (x) = x3 — нечетная функция.Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичный круг с положительным и отрицательным углом, как на рисунке 7. Синус положительного угла равен y.y. Синус отрицательного угла равен −y.−y. Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице 2.
Рисунок 7
| sin t = ysin (−t) = — ysin t ≠ sin (−t) sin t = ysin (−t) = — ysin t ≠ sin (−t) | cos t = xcos (−t) = xcos t = cos (−t) cos t = xcos (−t) = xcos t = cos (−t) | tan (t) = yxtan (−t) = — yxtan t ≠ tan (−t) tan (t) = yxtan (−t) = — yxtan t ≠ tan (−t) |
| сек t = 1xsec (−t) = 1xsec t = sec (−t) sec t = 1xsec (−t) = 1xsec t = sec (−t) | csc t = 1ycsc (−t) = 1 − ycsc t ≠ csc (−t) csc t = 1ycsc (−t) = 1 − ycsc t ≠ csc (−t) | детская кроватка t = xycot (−t) = x − ycot t ≠ детская кроватка (−t) детская кроватка t = xycot (−t) = x − ycot t ≠ детская кроватка (−t) |
Таблица 2
Четные и нечетные тригонометрические функции
Четная функция — это функция, в которой f (−x) = f (x).f (−x) = f (x).
Нечетная функция — это функция, в которой f (−x) = — f (x) .f (−x) = — f (x).
Косинус и секанс четные:
cos (−t) = cos tsec (−t) = sec tcos (−t) = cos tsec (−t) = sec tСинус, тангенс, косеканс и котангенс нечетные:
sin (−t) = — sin ttan (−t) = — tan tcsc (−t) = — csc tcot (−t) = — cot tsin (−t) = — sin ttan (−t) = — tan tcsc ( −t) = — csc tcot (−t) = — cot tПример 4
Использование четных и нечетных свойств тригонометрических функций
Если секанс угла tt равен 2, каков секанс угла −t? −t?
Решение
Секанс — четная функция.Секущая угла равна секущей его противоположности. Таким образом, если секанс угла tt равен 2, секанс угла −t − t также равен 2.
Попробуй # 4
Если котангенс угла tt равен 3,3, то каков котангенс угла −t? −t?
Распознавание и использование основных идентичностей
Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности. Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены.Обычно идентичность можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Фундаментальные личности
Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции могут быть связаны с функциями синуса и косинуса с помощью следующих основных соотношений:
tant = sintcosttant = sintcost cott = 1tant = costintcott = 1tant = costintПример 5
Использование идентичностей для оценки тригонометрических функций
- Учитывая sin (45 °) = 22, cos (45 °) = 22, sin (45 °) = 22, cos (45 °) = 22, оцените tan (45 °).загар (45 °).
- Дано sin (5π6) = 12, cos (5π6) = — 32, sin (5π6) = 12, cos (5π6) = — 32, вычисляем sec (5π6) .sec (5π6).
Решение
Поскольку мы знаем значения синуса и косинуса для этих углов, мы можем использовать тождества для оценки других функций.
-
tan (45 °) = sin (45 °) cos (45 °) = 2222 = 1tan (45 °) = sin (45 °) cos (45 °) = 2222 = 1 -
сек (5π6) = 1cos (5π6) = 1−32 = −231 = −23 = −233sec (5π6) = 1cos (5π6) = 1−32 = −231 = −23 = −233
Попробуй # 5
Вычислить csc (7π6).csc (7π6).
Пример 6
Использование тождеств для упрощения тригонометрических выражений
Упростите secttant.secttant.
Решение
Мы можем упростить это, переписав обе функции в терминах синуса и косинуса.
sec ttan t = 1cos tsin tcos t = 1cos t · cos tsin t Умножьте на обратную величину. = 1sin t = csc t Упростите и используйте тождество. sec ttan t = 1cos tsin tcos t = 1cos t · cos tsin t Умножьте на обратную величину. 1sin t = csc t Упростите и используйте идентичность.Показав, что secttantsecttant можно упростить до csct, csct, мы фактически установили новую идентичность.
сектант = csctsecttant = csctПопробуй # 6
Упростить (тант) (стоимость). (Тант) (стоимость).
Альтернативные формы пифагорейской идентичности
Мы можем использовать эти фундаментальные тождества, чтобы вывести альтернативные формы пифагорейской идентичности, cos2t + sin2t = 1. cos2t + sin2t = 1. Одна форма получается делением обеих частей на cos2t.cos2t.
cos2tcos2t + sin2tcos2t = 1cos2t1 + tan2t = sec2tcos2tcos2t + sin2tcos2t = 1cos2t1 + tan2t = sec2tДругая форма получается делением обеих частей на sin2t.sin2t.
cos2tsin2t + sin2tsin2t = 1sin2tcot2t + 1 = csc2tcos2tsin2t + sin2tsin2t = 1sin2tcot2t + 1 = csc2tАльтернативные формы пифагорейской идентичности
1 + tan2t = sec2t1 + tan2t = sec2t cot2t + 1 = csc2tcot2t + 1 = csc2tПример 7
Использование идентичностей для связи тригонометрических функций
Если cos (t) = 1213cos (t) = 1213 и tt находится в квадранте IV, как показано на рисунке 8, найдите значения других пяти тригонометрических функций.
Рисунок 8
Решение
Мы можем найти синус, используя тождество Пифагора, cos2t + sin2t = 1, cos2t + sin2t = 1, и остальные функции, связав их с синусом и косинусом.
(1213) 2 + sin2t = 1sin2t = 1− (1213) 2sin2t = 1−144169sin2t = 25169sin t = ± 25169sin t = ± 25169sin t = ± 513 (1213) 2 + sin2t = 1sin2t = 1− (1213) 2sin2t = 1 −144169sin2t = 25169sin t = ± 25169sin t = ± 25169sin t = ± 513Знак синуса зависит от значений y в квадранте, где расположен угол. Поскольку угол находится в квадранте IV, где значения y отрицательны, его синус отрицательный, −513. − 513.
Остальные функции можно вычислить с помощью тождеств, связывающих их с синусом и косинусом.
tan t = sin tcos t = −5131213 = −512sec t = 1cos t = 11213 = 1312csc t = 1sin t = 1−513 = -135cot t = 1tan t = 1−512 = −125tan t = sin tcos t = −5131213 = −512 сек t = 1cos t = 11213 = 1312csc t = 1sin t = 1−513 = -135cot t = 1tan t = 1−512 = −125Попробовать # 7
Если sec (t) = — 178sec (t) = — 178 и 0 Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция.Тригонометрические функции периодические. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или 2π, 2π приведет к одинаковым выходным данным для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты. Другие функции также могут быть периодическими. Например, продолжительность месяцев повторяется каждые четыре года. Если xx представляет собой продолжительность, измеряемую в годах, а f (x) f (x) представляет количество дней в феврале, тогда f (x + 4) = f (x).е (х + 4) = е (х). Этот образец повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и 4 годами ранее. Положительное число 4 — это наименьшее положительное число, которое удовлетворяет этому условию и называется периодом. Период — это самый короткий интервал, в течение которого функция выполняет один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней. Период PP повторяющейся функции ff — это число, представляющее интервал, такой что f (x + P) = f (x) f (x + P) = f (x) для любого значения x.x. Период функций косинуса, синуса, секанса и косеканса равен 2π.2π. Период функций касательной и котангенса равен π.π. Найдите значения шести тригонометрических функций угла tt по рисунку 9 . Рисунок 9 Найдите значения шести тригонометрических функций угла tt по рисунку 10. Рисунок 10 Если sin (t) = — 32andcos (t) = 12, findsec (t), csc (t), tan (t), cot (t).sin (t) = — 32 и cos (t) = 12, findsec (t), csc (t), tan (t), cot (t). sin (t) = 22 и cos (t) = 22, findsec (t), csc (t), tan (t) и cot (t) sin (t) = 22andcos (t) = 22, findsec (t), csc (t), tan (t) и cot (t) Мы научились оценивать шесть тригонометрических функций для общих углов первого квадранта и использовать их в качестве опорных углов для углов в других квадрантах.Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерное программное обеспечение. Если в калькуляторе есть режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем производить вычисления. Вычисление касательной функции с помощью научного калькулятора в отличие от графического калькулятора или системы компьютерной алгебры похоже на вычисление синуса или косинуса: введите значение и нажмите клавишу TAN. Для обратных функций может не быть каких-либо специальных клавиш с надписью CSC, SEC или COT.В этом случае функция должна быть вычислена как обратная величина синуса, косинуса или тангенса. Если нам нужно работать с градусами, а наш калькулятор или программное обеспечение не имеет режима градусов, мы можем ввести градусы, умноженные на коэффициент преобразования π180π180, чтобы преобразовать градусы в радианы. Чтобы найти секущую 30 °, 30 °, мы могли бы нажать Заданная величина угла в радианах , используйте научный калькулятор, чтобы найти косеканс. Учитывая угловую меру в радианах, используйте графическую утилиту / калькулятор, чтобы найти косеканс. Вычислите косеканс 5π7.5π7. Для научного калькулятора введите следующую информацию: Попробуй # 10 Вычислите котангенс −π8. − π8. Могут ли значения синуса и косинуса радианной меры когда-либо быть равными на интервале [0,2π), [0,2π)? Если да, то где? Каким должен быть косинус ππ градусов? Объясните свои рассуждения. Для любого угла во втором квадранте, если бы вы знали синус угла, как бы вы могли определить косинус угла? Опишите секущую функцию. Тангенс и котангенс имеют период π.π. Что это говорит нам о выходе этих функций? Для следующих упражнений найдите точное значение каждого выражения. В следующих упражнениях используйте исходные углы для оценки выражения. Если sint = 34, sint = 34 и tt находится в квадранте II, найдите стоимость, секту, csct, tant, стоимость, секту, csct, tant и cott.cott. Если cost = −13, cost = −13 и tt находится в квадранте III, найдите sint, sect, csct, tant, sint, sect, csct, tant и cott.Котт. Если tant = 125, tant = 125 и 0≤t <π2,0≤t <π2, найдите sint, cost, sect, csct, andcott.sint, cost, sect, csct иcott. Если sint = 32sint = 32 и cost = 12, cost = 12, найдите sect, csct, tant, sect, csct, tant и cott.cott. Если sin40 ° ≈0,643sin40 ° ≈0,643 и cos40 ° ≈0,766, cos40 ° ≈0,766, найдите sec40 °, csc40 °, tan40 °, sec40 °, csc40 °, tan40 ° и cot40 ° .cot40 °. Если sint = 22, sint = 22, что такое sin (−t)? Sin (−t)? Если стоимость = 12, стоимость = 12, что такое cos (−t)? Cos (−t)? Если sect = 3.1, sect = 3.1, что такое sec (−t)? Sec (−t)? Если csct = 0,34, csct = 0,34, что такое csc (−t)? Csc (−t)? Если tant = −1,4, tant = −1,4, что такое tan (−t)? Tan (−t)? Если cott = 9,23, cott = 9,23, что такое детская кроватка (-t)? Cot (-t)? В следующих упражнениях используйте угол в единичной окружности, чтобы найти значение каждой из шести тригонометрических функций. Для следующих упражнений используйте графический калькулятор, чтобы вычислить до трех десятичных знаков. Для следующих упражнений используйте удостоверения, чтобы оценить выражение. Если tan (t) ≈2,7, tan (t) ≈2,7 и sin (t) ≈0,94, sin (t) ≈0,94, найти cos (t) .cos (t). Если tan (t) ≈1,3, tan (t) ≈1,3 и cos (t) ≈0,61, cos (t) ≈0,61, найти sin (t) .sin (t). Если csc (t) ≈3,2, csc (t) ≈3,2 и cos (t) ≈0,95, cos (t) ≈0,95, найти tan (t) .tan (t). Если cot (t) ≈0,58, cot (t) ≈0,58 и cos (t) ≈0,5, cos (t) ≈0,5, найти csc (t) .csc (t). Определите, является ли функция f (x) = 2sinxcosxf (x) = 2sinxcosx четной, нечетной или ни одной из них. Определите, является ли функция f (x) = 3sin2xcosx + secxf (x) = 3sin2xcosx + secx четной, нечетной или ни одной из них. Определите, является ли функция f (x) = sinx − 2cos2xf (x) = sinx − 2cos2x четной, нечетной или ни одной из них. Определите, является ли функция f (x) = csc2x + secxf (x) = csc2x + secx четной, нечетной или ни одной из них. В следующих упражнениях используйте тождества, чтобы упростить выражение. Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 15cos (1600d), h = 15cos (1600d), где hh представляет количество солнечных часов, а dd — день в году. Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света 10 февраля, 42 -й день в году. Укажите период функции. Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 16cos (1500d), h = 16cos (1500d), где hh представляет количество солнечных часов, а dd — день в году.Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света 24 сентября, 267-й день в году. Укажите период функции. Уравнение P = 20sin (2πt) + 100P = 20sin (2πt) +100 моделирует артериальное давление, P, P, где tt представляет время в секундах. (а) Определите кровяное давление через 15 секунд. б) Какое максимальное и минимальное артериальное давление? Высота поршня h, h в дюймах может быть смоделирована уравнением y = 3sinx + 1, y = 3sinx + 1, где xx представляет угол поворота коленчатого вала.Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55 ° 0,55 °. Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 5, y = 2cosx + 5, где xx представляет угол поворота коленчатого вала. Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55 ° 0,55 °. Период функции
Пример 8
Поиск значений тригонометрических функций
Решение
sin t = y = −32cos t = x = −12tan t = sin tcos t = −32−12 = 3sec t = 1cos t = 1−12 = −2csc t = 1sin t = 1−32 = −233cot t = 1tan t = 13 = 33sin t = y = −32cos t = x = −12tan t = sin tcos t = −32−12 = 3sec t = 1cos t = 1−12 = −2csc t = 1sin t = 1−32 = — 233котт t = 1тан t = 13 = 33 Попробовать # 8
Пример 9
Определение значения тригонометрических функций
Решение
сек t = 1cos t = 112 = 2csc t = 1sin t = 1−32−233tan t = sin tcos t = −3212 = −3cot t = 1tan t = 1−3 = −33sec t = 1cos t = 112 = 2csc t = 1sin t = 1−32−233tan t = sin tcos t = −3212 = −3cot t = 1tan t = 1−3 = −33 Попробовать # 9
Оценка тригонометрических функций с помощью калькулятора
Пример 10
Оценка косеканса с использованием технологии
Решение
7.Упражнения из 4 частей
Устные
1. Алгебраические
Графический
Технологии
Расширения
Реальные приложения
72.



 Аннино, Варшавское шоссе, д. 143А В магазине 2 шт., забирайте сегодня В корзину
Аннино, Варшавское шоссе, д. 143А В магазине 2 шт., забирайте сегодня В корзину 10к2 По предзаказу на завтра, после 11:00 В корзину
10к2 По предзаказу на завтра, после 11:00 В корзину 20Г По предзаказу на завтра, после 11:00 В корзину
20Г По предзаказу на завтра, после 11:00 В корзину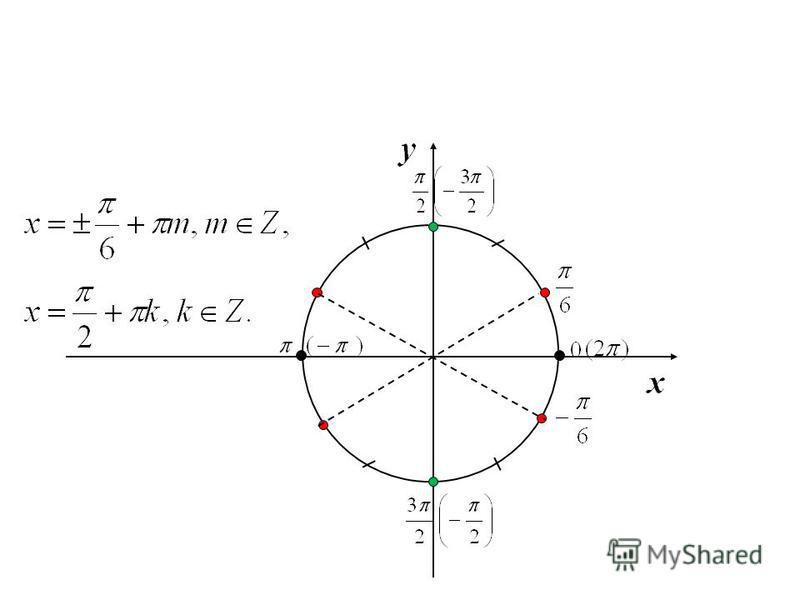 Люблино, ул. Люблинская, д. 61 По предзаказу на завтра, после 11:00 В корзину
Люблино, ул. Люблинская, д. 61 По предзаказу на завтра, после 11:00 В корзину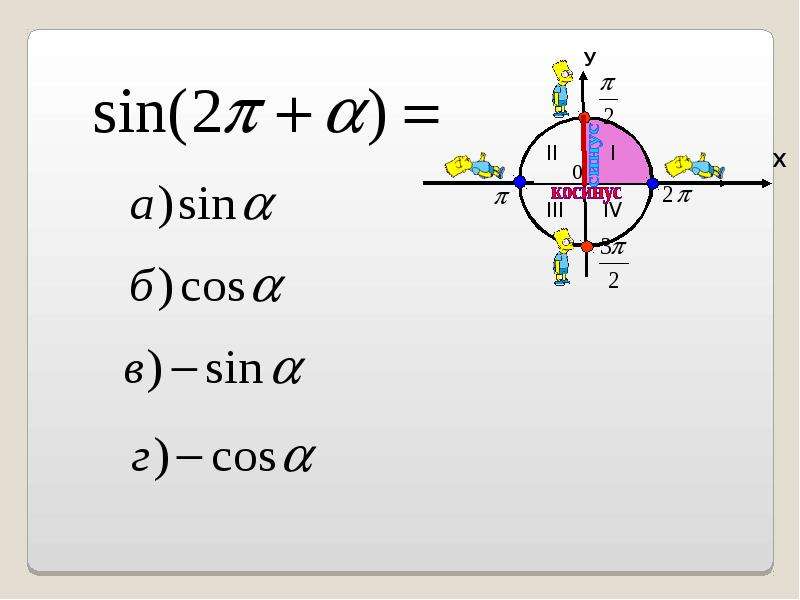 , р.п. Андреевка, ул. Жилинская, стр. 1 По предзаказу на завтра, после 11:00 В корзину
, р.п. Андреевка, ул. Жилинская, стр. 1 По предзаказу на завтра, после 11:00 В корзину Озерная, ул. Озерная, д. 42 По предзаказу на завтра, после 11:00 В корзину
Озерная, ул. Озерная, д. 42 По предзаказу на завтра, после 11:00 В корзину Савеловская, ул. Сущевский Вал, д. 9, строение 7 По предзаказу на 10 мая, после 11:00 В корзину
Савеловская, ул. Сущевский Вал, д. 9, строение 7 По предзаказу на 10 мая, после 11:00 В корзину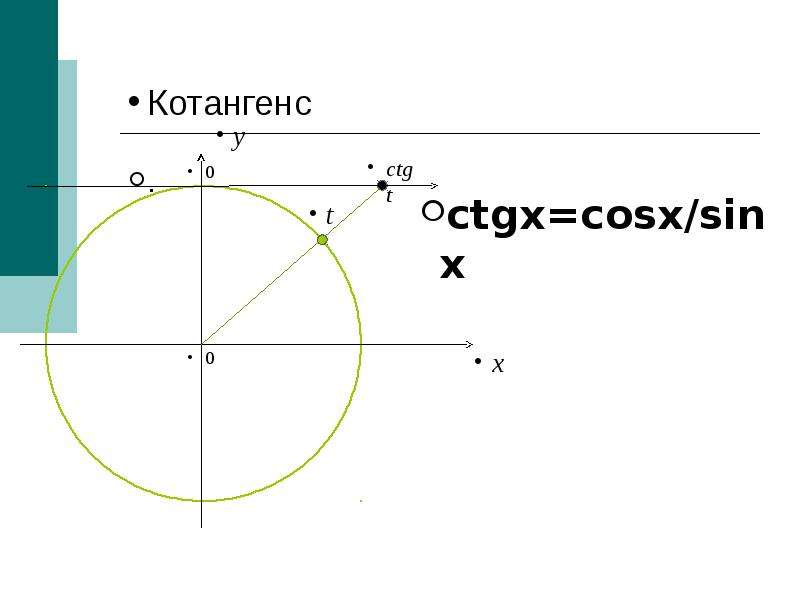 Тушинская, ш. Волоколамское, д. 92к2 По предзаказу на завтра, после 12:00 В корзину
Тушинская, ш. Волоколамское, д. 92к2 По предзаказу на завтра, после 12:00 В корзину Воскресенск, ул. Менделеева, д. 12 По предзаказу на завтра, после 11:00 В корзину
Воскресенск, ул. Менделеева, д. 12 По предзаказу на завтра, после 11:00 В корзину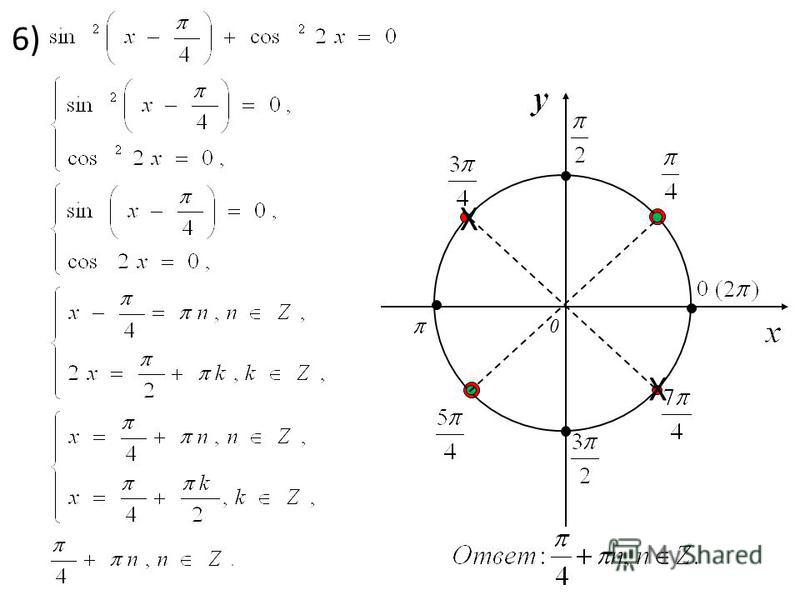 Жуковский, ул. Гагарина, д. 24 По предзаказу на завтра, после 11:00 В корзину
Жуковский, ул. Гагарина, д. 24 По предзаказу на завтра, после 11:00 В корзину Коломна, пр-т Кирова, д. 20А По предзаказу на завтра, после 11:00 В корзину
Коломна, пр-т Кирова, д. 20А По предзаказу на завтра, после 11:00 В корзину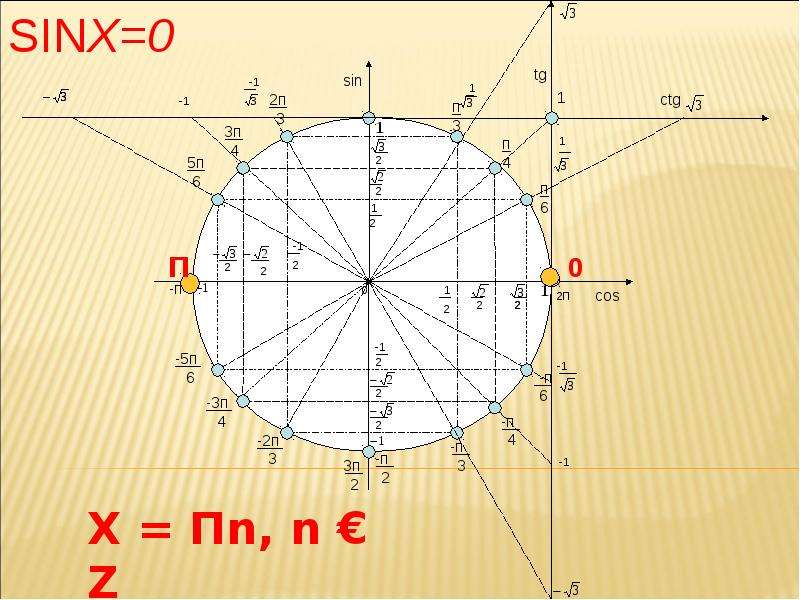 Московский, 1-й микрорайон, д. 32А По предзаказу на завтра, после 11:00 В корзину
Московский, 1-й микрорайон, д. 32А По предзаказу на завтра, после 11:00 В корзину 76 По предзаказу на завтра, после 11:00 В корзину
76 По предзаказу на завтра, после 11:00 В корзину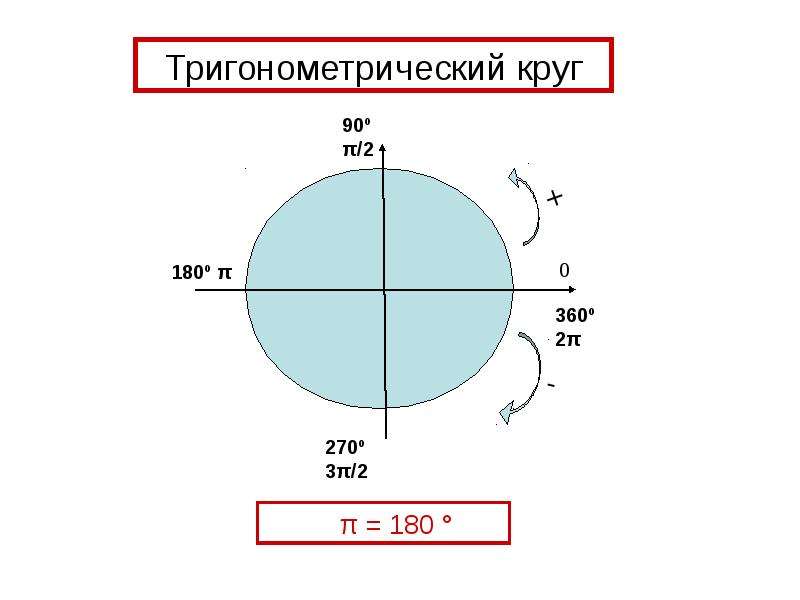 Серпухов, ул. Ворошилова, д. 82 По предзаказу на завтра, после 11:00 В корзину
Серпухов, ул. Ворошилова, д. 82 По предзаказу на завтра, после 11:00 В корзину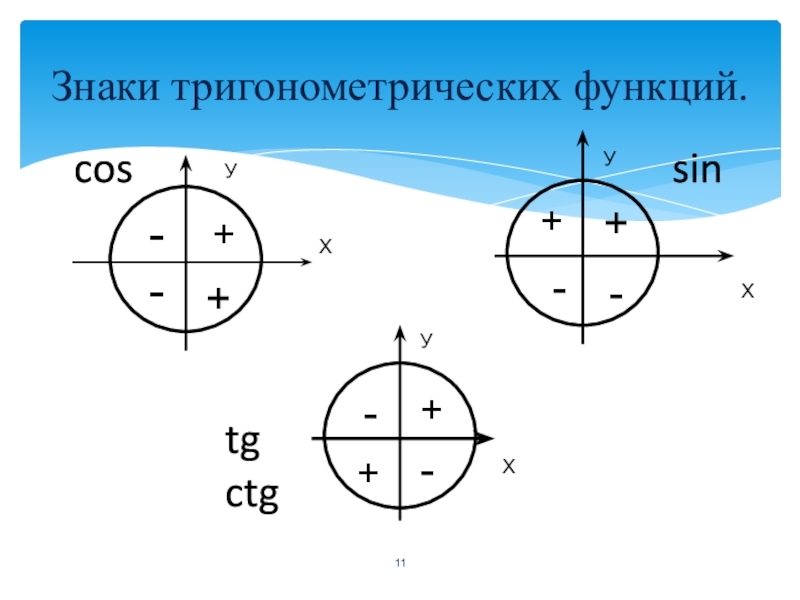 Чехов, Вишневый бульвар, д. 3-1 По предзаказу на завтра, после 11:00 В корзину
Чехов, Вишневый бульвар, д. 3-1 По предзаказу на завтра, после 11:00 В корзину 58, строение 7
58, строение 7 Генерала Белова, д. 29
Генерала Белова, д. 29 Косино,
Косино,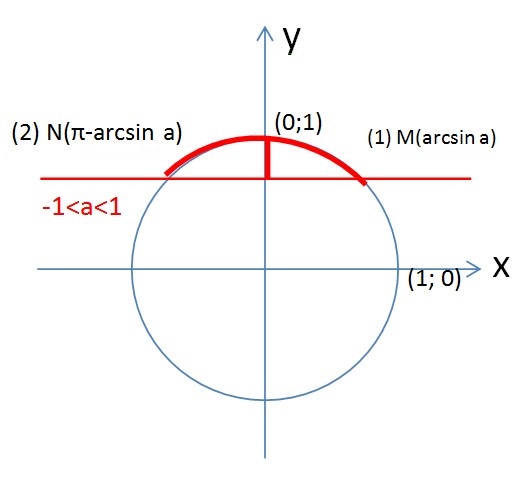 Люблинская, д. 61
Люблинская, д. 61 МЦД D2 Щербинка,
МЦД D2 Щербинка,