Как работает модулятор: как выбрать лучший, как настроить, принципы работы

Как работает кольцевой балансный модулятор

Р, 1955, №6

Часто применяющийся в аппаратуре дальней связи кольцевой балансный модулятор, схема которого приведена на рис. 1, в настоящее время начинает использоваться радиолюбителями-коротковолновиками для преобразования частот в диапазонных возбудителях с кварцевой стабилизацией (см. статью Л. Лабутина «Диапазонный возбудитель с кварцевой стабилизацией» в «Радио» № 5 за 1955 год). Это объясняется тем, что такой модулятор даёт на выходе наименьшее по сравнению с другими типами преобразователей количество вредных дополнительных комбинационных частот.

Рис. 1. Принципиальная схема кольцевого балансного модулятора

Для того чтобы понять, как работает кольцевой балансный модулятор, разберёмся сначала в том, что происходит в цепи, состоящей из генератора переменного напряжения, диода и батареи с переключателем П1, позволяющим изменять направление её включения (рис. 2, а).

Рис. 2. а — принципиальная схема, поясняющая принцип действия кольцевого балансного модулятора; б — графическое изображение тока в цепи в зависимости от направления включения батареи.

Известно, что ток через диод может протекать только в одном направлении. Это направление называют прямым. Если напряжение батареи выбрать больше амплитуды напряжения генератора, то, когда переключатель П1 будет находиться в положении 1, в цепи потечёт пульсирующий ток, а при положении 2 переключателя П1 тока в цепи не будет (рис. 2, б). При включении в такую цепь первичной обмотки трансформатора Тр1 в его вторичной обмотке будет наводиться напряжение, пропорциональное напряжению генератора, только тогда, когда переключатель П1 установлен в положение 1. Меняя полярность включения батареи, мы изменяем сопротивление диода от некоторой малой величины Ri, зависящей от свойств диода (переключатель находится в положении 1, диод открыт), до очень большой величины (переключатель П1 установлен в положение 2, диод закрыт). В кольцевом балансном модуляторе одно из двух преобразуемых напряжений, имеющее частоту f₁ подаётся на обмотку I трансформатора Тр1. Второе напряжение, имеющее частоту f₂, подаётся на средние точки обмоток II трансформаторов Tp1 и Тр2 и служит для изменения сопротивления диодов. Его частота f₂ должна быть больше частоты f₁ На рис. 3, а и б показаны эквивалентные схемы кольцевого балансного модулятора для двух полупериодов напряжения с частотой f₂. На схеме сплошными стрелками обозначено направление тока с частотой f₂, а пунктирными — с частотой f₁. Ток с частотой f₂ не может создать напряжения в обмотке I трансформатора Тр2, так, как он протекает в половинах катушки II в разные стороны. Создать напряжение в обмотке I трансформатоpa Tp2 может ток, протекающий по обмотке II в одном направлении. Величина этого тока пропорциональна мгновенному значению напряжения с частотой f₁, а направление изменяется через каждый полупериод частоты f₂. На рис. 4 показаны напряжения Uf₁, Uf₂ и U_Rн в случае, когда частота f₂ в десять раз больше частоты f₁.

Рис. 3. Эквивалентные схемы кольцевого балансного модулятора для двух полупериодов несущей частоты

Известно, что всякую периодически изменяющуюся во времени величину, в частности и напряжение U_Rн, можно разложить на сумму величин, изменяющихся во времени по синусоидальному закону. Для того чтобы определить амплитуды и частоты синусоидальных напряжений, из которых состоит выходное напряжение U_Rн, нужно познакомиться с векторным изображением периодически изменяющихся во времени величин.

Рис. 4. Зависимость от времени преобразуемых и выходного напряжений кольцевого балансного модулятора.

Представим себе неподвижный вектор ОА, вокруг начала которого (точка О) в плоскости рис. 5, а вращается с постоянной угловой скоростью ω=2πf рад/сек прямая. Точка О делит эту прямую на положительную и отрицательную полупрямые. Величина проекции вектора ОА на эту прямую Оа будет изменяться во времени по синусоидальному закону. Проекция какого-либо другого вектора на эту же ось будет изображаться синусоидой, сдвинутой по фазе по отношению к первой. Амплитуда этой синусоиды будет равна абсолютной величине этого вектора, а сдвиг фазы в угловой мере будет соответствовать углу между векторами. Таким образом, любой изменяющейся во времени по синусоидальному закону с частотой f величине будет соответствовать неподвижный вектор, имеющий определённую величину и положение в плоскости рис. 5, а. На рис. 5, а показаны два сдвинутые на 180° вектора, имеющие одинаковую величину. Соответствующие им синусоиды показаны на рис. 5, б. На рис. 5, в показана зависимость амплитуды колебаний, или, что то же самое, величины этих векторов от времени. Таким образом, вектор OA изображает в плоскости рис. 5, а синусоидальное напряжение и с частотой f, поэтому его можно назвать «вектором величины u». Если синусоидальное напряжение модулировано по амплитуде, то величина изображающего его вектора изменяется во времени. На рис. 6 показаны модулированное напряжение и зависимость соответствующего ему изображающего вектора от времени, причём частота f₂ (несущая) выбрана в десять раз больше частоты модулирующего напряжения f₁, т. е. соотношение между ними такое же, как и для рис. 4. Вектор, изменяющийся во времени, можно получить, складывая вектор постоянной величины с вектором, величина и направление которого меняются (рис. 7, а). Нетрудно видеть, что период изменения его величины должен быть равен периоду модулирующей частоты f₁. В свою очередь и этот вектор можно получить, складывая два равномерно вращающихся в разные стороны вектора.

Рис. 5. Векторное изображение синусоидальных напряжений

Расположение вращающихся векторов в зависимости от времени показано на рис. 7, б. Как видно из рис. 7, а и б, за время одного периода модулирующей частоты f₁ эти векторы сделают один оборот. Следовательно, вектор, поворачивающийся против часовой стрелки, будет иметь по отношению к вращающейся по часовой стрелке с угловой скоростью ω=2πf₂ рад/сек прямой, угловую скорость, равную сумме их скоростей, т. е. напряжение, соответствующее этому вращающемуся вектору, будет иметь частоту, равную сумме частот несущего и модулирующего напряжений.

Рис. 6. Модулированное напряжение и зависимость изображающего его вектора от времени

Рассуждая таким же образом, легко увидеть, что частота напряжения, соответствующего вектору, вращающемуся по часовой стрелке, будет равна разности несущей и модулирующей частот.

Рис. 7. Временное и векторное изображения напряжений боковых частот модулированного колебания

Таким образом, напряжение, показанное на рис. 7, в, соответствующее вектору рис. 7, а, является суммой двух синусоидальных напряжений с частотами f₂+f₁ и f₂-f₁. Это напряжение очень похоже на выходное напряжение кольцевого балансного модулятора U_Rн (рис. 4). Некоторое различие в формах этих напряжений объясняется тем, что на выходе кольцевого балансного модулятора, кроме суммарной и разностной частот преобразуемых колебаний, имеются ещё напряжения с частотами n * f₁+-f₂, где n может принимать значения 3, 5, 7 и т. д. Однако эти напряжения легко могут быть отфильтрованы.

Желающие более подробно познакомиться с анализом работы кольцевого балансного модулятора могут найти интересующие их сведения в книге Н. Баева и К. Егорова «Основы дальней связи» (Связьиздат, 1948 г.).

С. Ершов

BACK

Квадратурный Модулятор и Демодулятор — пример работы

Приветствую, перед прочтением статьи рекомендую почитать про модуляцию и манипуляцию, амплитудную и фазовую манипуляцию и спектр сигнала. ix=cosx+isinx. Сместили спектр сигнала вниз по частоте и чтобы подавить вторую боковую составляющую, мы пропустили через фильтр нижних частот (ФНЧ). На выходе получили две квадратуры Baseband сигнала Re и Im. На входе был ВЧ сигнал. 

Квадратурный демодулятор преобразует вещественный ВЧ сигнал в его низкочастотный эквивалент.

С помощью такого демодулятора, можно преобразовать сигнал с любой полосовой модуляцией. Главное, чтобы спектр сигнала, уложился в полосу пропускания этого фильтра. 

Квадратурный модулятор

На входе есть квадратуры Baseband сигнала, а на выходе ВЧ колебание. Он выглядит проще чем демодулятор, фильтры не нужны, потому что изначально, вторая половинка спектра уже подавлена. 

Нужно baseband сигнал умножить на комплексную экспоненту и сместить спектр вверх по частоте. Откуда взялся минус на картинке? -sin(2pift). Ниже есть формулы объясняющие этот минус. 

I и Q это квадратуры baseband сигнала, те которые были на входе квадратурного модулятора. cos и sin комплексная экспонента по формуле Эйлера.

• s(t) – вещественный сигнал;
• z(t) – аналитический сигнал;
• zв(t) – комплексная огибающая, сигнал без несущей;
• А(t) – закон изменения амплитуды от времени;
• θ(t) – закон изменения мгновенной фазы от времени;
• ω – угловая частота;
• I и Q – квадратуры.

Если мы раскроем скобки, получится полная сумма, но из этой суммы мы оставили только вещественную часть, а то что было с мнимой единицей мы отбросили. s(t) реальная часть аналитического сигнала. 

Квадратурный модулятор это устройство, которое преобразует baseband сигнал в вещественный сигнал. С помощью квадратурного модулятора мощно сформировать сигнал с любой модуляцией.

Если мы знаем квадратуру, то можем вычислить амплитуду и фазу. 

Пример того, как работает модулятор

Рассмотрим простой пример. Нарисовали график с точками S1-S4. На схеме изображен модулятор, что мы должны подавать на входы модулятора, чтобы получить четверичную фазовую манипуляцию?

Сначала получаем S1, потом S2, затем S3 и S4.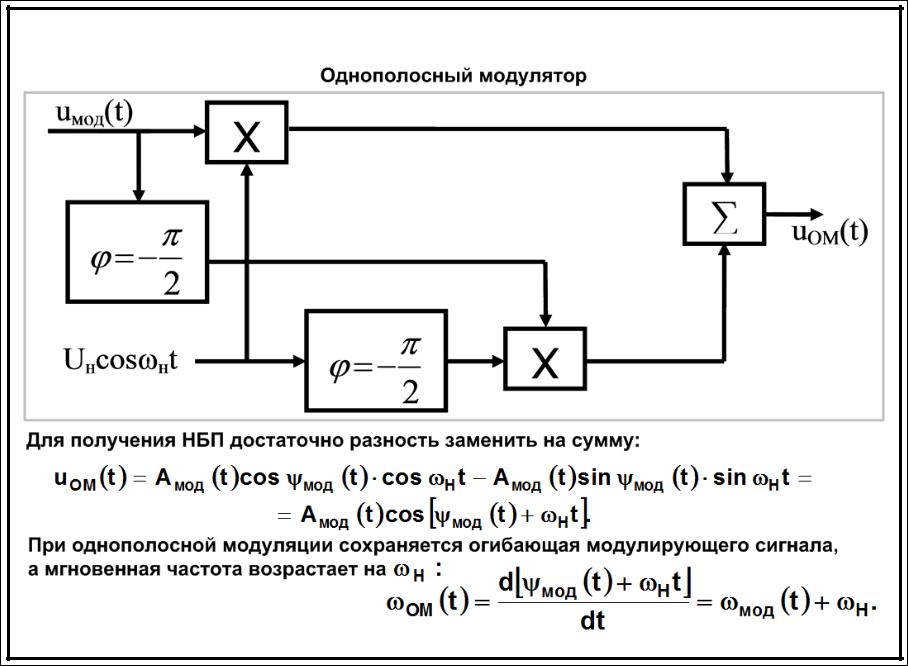 На входы модулятора нужно подавать координаты точек (таблица). Таким образом задаем сигналы для фазовой манипуляции и QAM, просто через координаты точек на прямоугольной системе координат. 

Спасибо за прочтение статьи, все статьи на тему радиосвязи вы найдете в разделе радиосвязь. Если есть вопросы задавайте в комментариях! 

Поделиться с друзьями:

Твитнуть

Поделиться

Поделиться

Отправить

Класснуть

Как работает модуляция? | Tait Radio Academy

Тема прогресса:

← Вернуться к уроку

Частота радиочастотного канала лучше всего понимается как частота несущей волны.
Несущая волна — это чистая волна постоянной частоты, немного похожая на синусоиду. Сам по себе он не несет много информации, к которой мы можем относиться (например, речь или данные).

Чтобы включить речевую информацию или информацию данных, необходимо наложить другую волну, называемую входным сигналом, поверх несущей волны. Этот процесс наложения входного сигнала на несущую называется модуляцией. Другими словами, модуляция изменяет форму несущей волны, чтобы каким-то образом закодировать речь или данные, которые нас интересовали. Модуляция подобна сокрытию кода внутри несущей волны.

Напомним, что любая волна имеет три основных свойства:

1) Амплитуда – высота волны
2) Частота – количество волн, проходящих в данную секунду
3) Фаза – где фаза в любой данный момент.

Существуют различные стратегии модуляции несущей волны. Во-первых, пользователь может настроить высоту держателя. Если высота входного сигнала изменяется в зависимости от громкости голоса пользователя, а затем добавляется к несущей, то амплитуда несущей будет изменяться в соответствии с входным сигналом, который был подан на нее. это называется 9Амплитудная модуляция 0003 или AM .

Также можно изменить частоту входного сигнала. Если этот входной сигнал добавить к чистой несущей, то частота несущей изменится. Таким образом, пользователи могут использовать изменения частоты для переноса речевой информации. Это называется частотной модуляцией или FM.

Эти две стратегии можно объединить для создания третьей схемы. Фактически любая стратегия, которая объединяет входной сигнал с несущей для кодирования речи или другой полезной информации, называется схемой модуляции.

Схемы модуляции могут быть аналоговыми или цифровыми. Схема аналоговой модуляции имеет входную волну, которая постоянно изменяется, как синусоида. В схеме цифровой модуляции все немного сложнее. Голос сэмплируется с определенной скоростью, затем сжимается и превращается в битовый поток — поток нулей и единиц — который, в свою очередь, превращается в волну определенного типа, которая затем накладывается на несущую.

Большой вопрос, зачем вообще модулировать несущие волны? Почему бы просто не использовать входной сигнал напрямую? В конце концов, он несет всю интересующую нас информацию и занимает всего несколько килогерц и полосу пропускания. Так почему бы не использовать его напрямую? Зачем вообще нужны несущие и модуляция?

Интересно, что входные сигналы могут передаваться (без несущей волны) очень низкочастотными электромагнитными волнами. Проблема, однако, в том, что для передачи этих очень низких частот потребуется совсем немного усиления. Сами входные сигналы не имеют большой мощности и требуют довольно большой антенны для передачи информации.

Чтобы связь была дешевой и удобной, а для передачи как можно большего количества информации требовалось меньше энергии, используются несущие системы с модулированными несущими.

    Следующая тема →

Как работает модуляция сигнала?

Чтобы понять, как происходит беспроводная передача данных, нам нужно понять: • Что такое частота? • Сигналы сообщений/данных • представление времени • частотное представление и почему оно важно? • Как работают фильтры? • Диапазоны связи FCC • Модуляция и демодуляция

Как работает модуляция сигнала?
 

Чтобы понять, как происходит беспроводная передача данных, нам нужно понять:

•    Что такое частота?
•    Сигналы сообщений/данных
•    представление времени
•    представление частоты, и почему это важно?
•    Как работают фильтры?
•    Полосы связи FCC
•    Модуляция и демодуляция
 

Что такое частота?
Частота — это единица, описывающая, как часто что-то колеблется или движется вперед и назад. Единицами являются Герц (Гц), или инверсия секунды. Что-то, колеблющееся 60 раз в секунду, имеет частоту 60 Гц. Для наших целей мы сосредоточимся на звуковых волнах (колебания атмосферного давления) и на том, как они передаются от радиостанции к вашему автомобилю в диапазоне сотен килогерц (или любой AM-радиостанции). У любой волны есть частота, у света, например. Обычно световые и другие высокочастотные волны (например, рентгеновские лучи, гамма-лучи, микроволны) представлены их длиной волны, а не частотой. Например, зеленый свет имеет длину около 400 нанометров. Вот картинка, показывающая соотношение единиц на бегущей волне:

 

Основные единицы измерения синусоиды.

При постоянной скорости сигнала длина волны и частота взаимозаменяемы. Однако это выходит за рамки данной статьи.

Сигналы сообщений различной сложности
Посылка сигнала, представляющего собой чистую синусоидальную волну, называется «тоном». Он не несет никакой реальной информации, да и звучит не очень хорошо. Вот изображение синусоиды со временем по оси X и напряжением по оси Y. Это 150 Гц для справки.

Однотональный сигнал (временной интервал)

Итак, зачем я вам это показываю? Давайте посмотрим на все более сложные сигналы во временной области. Вот двухтональный сигнал (два тона, сложенные вместе). Это та же самая синусоида выше, сложенная вместе с другой синусоидой с удвоенной частотой, 300 Гц.

Двухтональный сигнал (временная область)
 

Как насчет сигнала, состоящего из множества тонов различной частоты:
 

Многотональный сигнал (временная область)
 

Федеральная комиссия по связи США (FCC) оставила несколько диапазонов открытыми для личного использования в низкочастотных диапазонах, любителей и другого общего использования в «диапазонах ISM» (промышленных, научных, медицинских). Здесь работают Wi-Fi, рации, беспроводные датчики и другие коммерческие устройства. Давайте снова поговорим о частотах! Человеческое ухо имеет диапазон от 20 Гц до 20 кГц. Что, если наша радиостанция AM работает на частоте 680 кГц? Как радиовышка поднимает звук до такой частоты? Как это не мешает другим станциям? Как приемник возвращает частоту сигнала в слышимый диапазон?

 

Модуляция
Давайте отойдем от частотной области и вернемся во временную область. Я снова широко использую свое предыдущее заявление об отказе от ответственности: оно чрезмерно упрощено и пропускает многие детали! Это только для понимания концепции. Причина, по которой я это говорю, заключается в том, что математика лучше всего работает во временной области, а графическое представление лучше всего работает в частотной области.

Модуляция берет сигнал с низких частот (сообщение) и переводит его на более высокую частоту (несущая). Идея проста: умножьте свое сообщение на высокочастотную несущую, например 680 кГц. Вуаля, это АМ-радио! Подожди, неужели это так просто? Рассмотрим несколько математических соотношений. В этом случае тета — это сообщение (звуковой материал), а фи — носитель (например, AM-радиочастота).

 

Наше AM-решение включает в себя умножение сигналов, но это трудно представить во временной или частотной области, поскольку мы видели только то, как выглядят тоны. Но изящные отношения выше показывают нам, что два перемноженных сигнала могут быть представлены как два сигнала, сложенные вместе! Теперь легко построить умноженный сигнал в частотной области.
 

Одиночный тон (150 Гц), модулированный на несущей (1000 Гц)
 

На этом рисунке мы умножили тон 150 Гц на несущую 1000 Гц. В приведенной выше таблице показано, что мы ожидаем два сигнала половинной мощности на частотах 1000-150 и 1000+150 Гц, 850 Гц и 1150 Гц. Как выглядит наш звуковой байт после модуляции?
 

Модуляция звукового клипа до 700 кГц
 

Как и ожидалось, мы видим два сигнала. Один — носитель + сообщение, другой — носитель — сообщение (даже обратите внимание, как перевернуто).

Вот грубое изображение частотного спектра AM и содержимого сигнала.

Демодуляция
Теперь поговорим о приемниках. Все сигналы начинаются с антенны, которая одновременно воспринимает все сигналы как один большой беспорядок. Задача антенны не в том, чтобы разобраться в мешанине данных, которые она собирает, а в том, что это работа тюнера и другого оборудования. Теория демодуляции сигнала идентична его модуляции, что достаточно удобно! Чтобы вернуть наш аудиосигнал обратно в «основную полосу», где его можно отправить на динамик, мы снова умножаем все на несущую.
 

Это куча математики, скобок и букв f повсюду. Но это правильно, и мы видим, что в результате получается четыре сигнала:

•    1/4 мощности сигнала, (2*несущая + сообщение)
•    1/4 мощности сигнала, (сообщение)
•    1/4 мощности сигнал, (2*несущая – сообщение)

•    1/4 мощности сигнал, (-сообщение)
 

Сразу отбросим термин с отрицательной частотой. Это математический артефакт, который довольно часто встречается, когда речь идет о модуляции и математике.