Движение по круговому движению: что это, как проехать, знаки :: Autonews

Правила кругового движения на машине 2023

Круговое движение на машине – это одно из основных элементов городского движения, и оно становится все популярнее с каждым годом. Круги облегчают трафик, уменьшают пробки и снижают риск аварий, но не всем водителям понятны правила их проезда. В этой статье мы рассмотрим основные правила кругового движения, действующие с 2023 года.

Введите круг в пункт назначения: так звучит девиз многих городов в мире. И это правда – несмотря на то, что круги могут показаться запутанными и сложными при первом взгляде, они удобны и функциональны. Однако многие водители не знают, как правильно ездить по кругу и в какую полосу движения нужно въезжать и выезжать. В этой статье вы узнаете об общих правилах и особенностях кругового движения в 2023 году.

Для того, чтобы безопасно и легко передвигаться по кругам, водитель должен знать, как вести себя на дороге и как сигнализировать о своих действиях другим участникам движения. Нарушение правил кругового движения может привести к аварии или затруднить движение на дороге. В этой статье мы рассмотрим правила безопасного проезда кругового движения и ответим на наиболее распространенные вопросы водителей о данном элементе городской инфраструктуры.

Содержание

1. Общие положения
2. Правила проезда кругового движения
3. Общие правила
4. Правила проезда кругового движения
5. Заключение
6. Сложные ситуации на кольце
7. Правила выезда с кругового движения
8. Правила поведения на круговом движении для пешеходов и велосипедистов
9. Пешеходы:
10. Велосипедисты:
11. Международные правила кругового движения на машине
12. Основные правила
13. Следование по полосам
14. Обгон и разворот
15. Пешеходы
16. Безопасность на дороге

Общие положения

Круговое движение на машине – это один из самых сложных видов дорожного движения. Водитель должен не только следить за своей машиной, но и учитывать движение других участников на круге, а также уступать им при необходимости. В этой статье мы рассмотрим основные правила кругового движения на машине.

• Перед заездом на круг необходимо убедиться в свободном движении на нем.
• Въезжая на круг, нужно уступить дорогу тем участникам, которые уже движутся по нему.
• При движении по кругу необходимо учитывать маневры других участников и правильно выбирать полосу движения.
• При выезде с круга необходимо выбирать соответствующую полосу и симметрично въезжающей на круг машине.
• При движении по кругу запрещается делать движения задом, остановки и стоянки.

Следование данным правилам позволит снизить риски происшествий на кругу, сохранить безопасность и комфорт участников дорожного движения.

Правила проезда кругового движения

Общие правила

Круговое движение представляет собой специальный вид перекрестка, где транспорт движется по кругу вместо пересечения путей друг друга. Оно позволяет уменьшить количество аварий и заставляет водителей быть осторожнее и более внимательными.

Правила проезда кругового движения установлены для обеспечения безопасности всех участников дорожного движения. Они являются обязательными для соблюдения всеми водителями.

Правила проезда кругового движения

Перед въездом на круговое движение необходимо снизить скорость и выбрать нужную полосу движения. При наличии разметки, следуйте указаниям стрелок и знаков дорожного движения.

При движении по круговому движению имейте при себе право уступить дорогу для других водителей, находящихся на полосах, расположенных справа от вас, если это требуется.

При съезде с кругового движения, оповестите других водителей заранее с помощью разворотного указателя поворота и выберите нужную полосу движения. Не подпускайте других водителей слишком близко и не меняйте полосу движения на последней секунде.

Заключение

Соблюдение правил проезда кругового движения является важным элементом общей безопасности на дороге. Не забывайте, что вы не едете в одиночку и ваше поведение на дороге влияет на всех участников дорожного движения.

Сложные ситуации на кольце

При круговом движении на машине нередко возникают сложные ситуации, особенно когда на кольце много машин.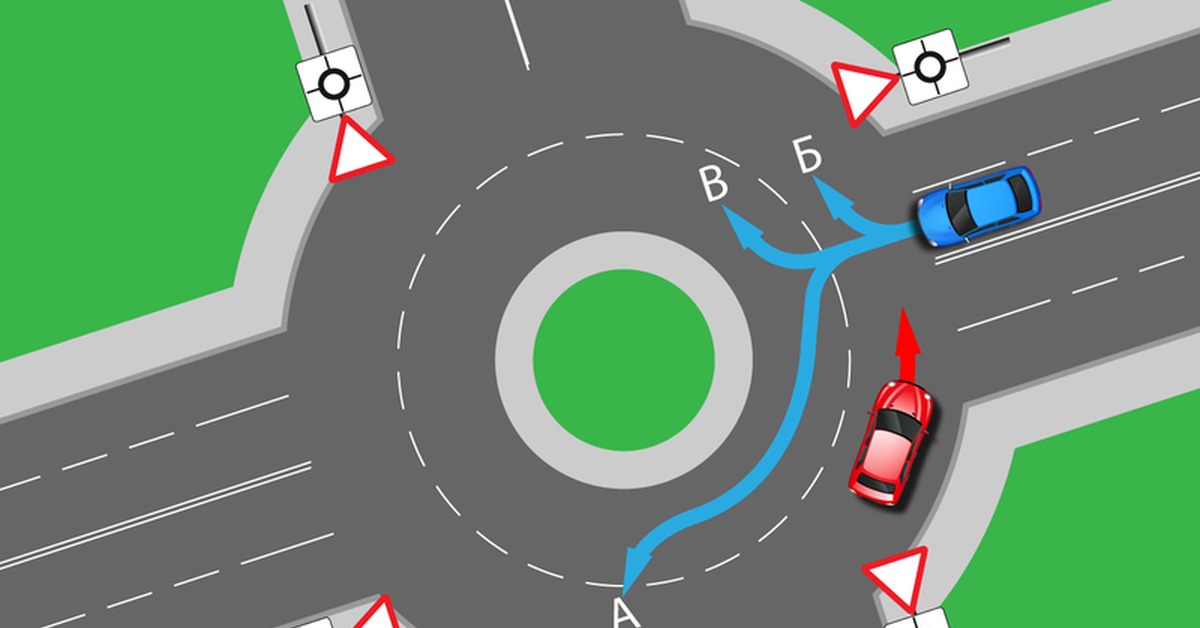 Одна из таких ситуаций — это когда на кольце есть несколько полос и вы хотите перестроиться на нужную полосу, но она занята другими машинами.

В такой ситуации нужно проявлять особую осторожность и следить за поведением других водителей на дороге. Важно не создавать аварийных ситуаций и не препятствовать движению других участников дорожного движения.

• При перестроении на нужную полосу следует проверять наличие машин в зеркалах заднего вида и делать сигнал поворота.
• Если машина начала перестроение, то не стоит ускорять передвижение, так как это может вызвать задержки на кольце и создать аварийную ситуацию.
• В случае, если не удалось перестроиться на нужную полосу и нужно выехать с кольца, необходимо сделать сигнал и начать выезжать заранее. Не следует совершать резкие маневры на кольце.

Правила выезда с кругового движения

При выезде с кругового движения необходимо заранее выбрать нужную полосу движения, ориентируясь на дорожные знаки и соблюдая правила движения.

Если на круговом движении предусмотрена специальная полоса для поворота налево, необходимо занять ее заранее, чтобы спокойно совершить маневр. В остальных случаях следует выезжать с круга по правой полосе.

Перед выездом с круга необходимо включить правый указатель поворота и остановиться на перекрестке, если есть необходимость. При этом не следует создавать помех другим участникам движения и тормозить перед выездом, а также менять полосу движения на круговом движении.

• Если водитель намерен продолжить движение по круговому движению, следует занять соответствующую полосу и не забывайте уступать дорогу при необходимости.
• При выезде с круга налево, водитель должен быть уверен, что нет других участников, которые могут ему помешать, а также соблюдать скоростной режим и дистанцию до других автомобилей на дороге.

Соблюдение правил выезда с кругового движения помогает избежать аварий и обеспечить безопасность на дороге.

Правила поведения на круговом движении для пешеходов и велосипедистов

Пешеходы:

Пешеходам запрещено пересекать дорогу на круговом движении, если нет соответствующего знака, разрешающего переходить.

При нахождении на круговом движении, пешеход должен двигаться только по тротуарам и специальным тротуарным дорожкам.

Если пешеход решил перейти дорогу, необходимо выбрать удобное место, где есть соответствующий знак разрешающий переход, и ожидать зеленый сигнал светофора.

Велосипедисты:

Велосипедисты могут двигаться по круговому движению с использованием специальной полосы.

Перед началом движения велосипедист должен убедиться в отсутствии на круговом движении пешеходов, также должен сигнализировать о своем намерении поворота.

Рекомендуется снижать скорость при нахождении на круговом движении и быть внимательным к другим участникам дороги.

Запрещено движение на велосипеде по тротуарам в местах, где есть специальные полосы на круговом движении для велосипедистов.

Международные правила кругового движения на машине

Основные правила

В большинстве стран существует общее правило движения по кругу: движение всегда происходит по часовой стрелке.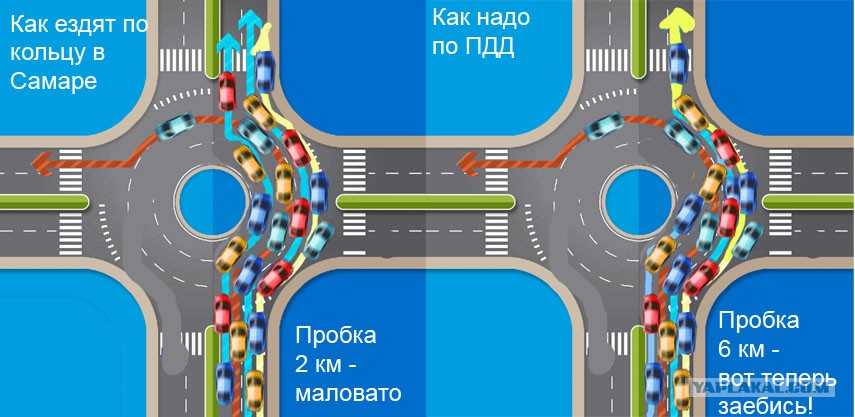 При въезде на круг необходимо уступить дорогу тем, кто уже находится на нем. Также водитель не должен выезжать на другую полосу движения, если не уверен, что сможет выполнить маневр безопасно.

Следование по полосам

При движении по кругу необходимо следовать указателям и сигналам светофора. Если на кругу есть несколько полос, то водитель должен предупредить о своих действиях с помощью поворотных сигналов и занять нужную полосу заблаговременно.

Обгон и разворот

Обгон на кругу запрещен, также нельзя выполнять разворот на нем. Если при движении по кругу необходимо совершить поворот налево, необходимо занять крайнюю левую полосу и проехать мимо поворота на кругу, а затем выполнить поворот.

Пешеходы

Пешеходам не рекомендуется перемещаться по кругу, но в случае необходимости они должны соблюдать правила пешеходного перехода. Водитель всегда должен быть готов к тому, что на кругу могут находиться пешеходы.

Безопасность на дороге

Помимо основных правил, водитель всегда должен следить за скоростью движения, расстоянием до других машин и дорожными знаками. При движении по кругу на машине необходимо быть особенно внимательным и осторожным, чтобы избежать аварий.

Круговое движение | это… Что такое Круговое движение?

У этого термина существуют и другие значения, см. Вращение (значения).

О разновидности перекрёстков: см. Круговой перекрёсток.

В физике кругово́е движе́ние — это вращение по кругу, т. е. это круговой путь по круговой орбите. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.

Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.

Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.

Содержание 1 Формулы для равномерного кругового движения 2 Постоянная скорость 3 Переменная скорость 4 Описание кругового движения в полярных координатах 5 Описание кругового движения в комплексных числах 6 Ссылки 7 См. также

Формулы для равномерного кругового движения

Рис. 1: Взаимосвязи векторов равномерного кругового движения; вектор Ω, представляющий вращение, перпендикулярен к плоскости орбиты.

Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна:

Скорость движения объекта равна

Угол поворота θ за время t равен:

Ускорение, вызванное изменением направления скорости, можно найти, если заметить, что скорость совершает полное изменение направления за то же самое время T, за которое объект делает один оборот. Тогда вектор скорости проходит путь длиной 2π v каждые T секунд, или:

и направлено радиально к центру.

Взаимосвязи векторов показаны на рис. 1. Ось вращения изображена вектором Ω, перпендикулярно плоскости орбиты и имеет величину ω = dθ / dt. Направление вектора

Ω выбрано в соответствии с правилом правой руки. По этому соглашению скорость это векторное произведение вида:

и есть вектор, перпендикулярный как Ω так и r ( t ), направленный по касательной к орбите и имеющий величину ω R. Аналогично, ускорение определяется как:

Оно представляет собой вектор, перпендикулярный как Ω так и v ( t ), имеющий величину ω |v| = ω²R и направление строго противоположно к r ( t ).

Постоянная скорость

В простейшем случае скорость, масса и радиус являются постоянными.

Рассмотрим тело массой один килограмм, движущееся по кругу радиуса один метр с угловой скоростью один радиан в секунду.

• Скорость: один метр в секунду
• Радиальное ускорение: один метр в секунду за секунду.
• Ускорение сообщается центростремителной силой один килограмм на метр в секунду за секунду, т. е. один ньютон.
• Импульс тела: один kg·m·s⁻¹.
• Момент инерции: один kg·m².
• Момент импульса: один kg·m²·s⁻¹.
• Кинетическая энергия: 1/2 джоуля.
• Длина окружности орбиты: 2π (~ 6.283) метров.
• Период движения: 2π секунд на один оборот.
• Частота: (2π)⁻¹герц.
• С точки зрения квантовой механики система находится в возбужденном состоянии с квантовым числом ~ 9.48·10³⁵.

Теперь рассмотрим тело массы m, движущееся по кругу радиуса r с угловой скоростью ω.

• Скорость: v = r·ω.
• Радиальное ускорение: a = r·ω ² = r ⁻¹·v ².
• Центростремительная сила: F = m·a = r·m·ω ² = r⁻¹·m·v ².
• Импульс тела: p = m·v = r·m·ω.
• Момент инерции: I = r ²·m.
• Момент импульса: L = r·m·v = r ²·m·ω = I·ω.
• Кинетическая энергия: E = 2⁻¹·m·v ² = 2⁻¹·r ²·m·ω ² = (2·m)⁻¹·p ² = 2⁻¹·I·ω ² = (2·I)⁻¹·L ² .
• Длина окружности орбиты: 2·π·r.
• Период движения: T = 2·π·ω ⁻¹.
• Частота: f = T ⁻¹ . (Вместо буквы f частота часто обозначается греческой буквой ν, которая, однако, часто неотличима от буквы
  v, используемой здесь для обозначения скорости).
• Квантовое число: J = 2·π·L h⁻¹

Переменная скорость

В круговом движении полную силу, приложенную к объекту, можно разложить на две составляющие: центростремительную, удерживающую тело на круговой орбите (т. е. меняющую направление вектора скорости), и тангенциальную, направленную по касательной к окружности и вызывающую изменение длины вектора скорости (т. е. меняющую скорость вращения тела по орбите). Величина центростремительной составляющей зависит от мгновенной скорости.

Для примера, когда камень привязан к концу верёвки, он подвергается воздействию силы, мы можем разложить силу на радиальную и боковую составляющие. Радиальная направлена к центру (вовнутрь) окружности и вызвана тем, что веревка сопротивляется удлинению. А боковая составляющая определяет — будет вращение камня ускоряться или замедляться.

Описание кругового движения в полярных координатах

Рис. 2: Полярные координаты для круговой траектории. Единичная окружность слева показывает изменение и единичных векторов и для малого приращения угла .

Траектория кругового движения тела может быть описана в полярной системе координат значениями фиксированного расстояние R от центра орбиты, являющейся точкой отсчёта, и угла ориентации θ (t) от некоторого фиксированного направления (рис. 2). Вектор перемещения является радиальным вектором от полюса до текущего положения:

где — единичный вектор, параллельный радиусу в момент t и направленный от полюса. Удобно также ввести единичный векторортогональный к , который назовём . Обычно его ориентация выбирается по направлению движения вдоль орбиты.

Скорость является производной перемещения по времени:

Поскольку радиус окружности является константой, радиальная составляющая скорости равна нулю. Единичный вектор имеет инвариантное по времени значение, так что при изменении времени его конец всегда лежит на окружности единичного радиуса, а угол θ такой же, как у . Если произошло малое приращение угла dθ за время dt, тогда описывает дугу единичной окружности со значением dθ (см. единичную окружность слева на рис. 2). Следовательно:

где направление изменения должно быть перпендикулярно к (или, другими словами, вдоль ), поскольку любое изменение d в направлении будет изменять величину . Знак положительный, потому что увеличение dθ влияет на объект и передвигается в направлении . Следовательно, скорость становится:

Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение есть производная скорости по времени:

Производная по времени от находится таким же путём, как и для . Опять же, есть единичный вектор, и его конец расположен на единичной окружности, а угол равен π/2 + θ. Следовательно, приращение угла dθ вектора перемещает по дуге на величину dθ, и поскольку перпендикулярен к , мы имеем:

где отрицательный знак необходим, чтобы сохранить перпендикулярным к . (Иначе угол между и будет уменьшаться с увеличением dθ, см. единичную окружность слева на рис. 2). Следовательно, ускорение равно:

Центростремительное ускорение — это радиальная составляющая, направленная по радиусу вовнутрь:

тогда как тангенциальная составляющая изменяет значение скорости:

Описание кругового движения в комплексных числах

Круговое движение можно описать с использованием комплексных чисел. Пусть — ось вещественных чисел, а — ось мнимых чисел. Тогда положение тела может быть задано в виде комплексного «вектора» :

где есть мнимая единица, и

есть угол комплексного вектора по отношению к вещественной оси как функция времени t. Поскольку радиус есть константа:

где точка означает дифференциал по времени. В этих обозначениях скорость имеет вид :

а ускорение:

Первое слагаемое направлено против вектора перемещения, а второе — перпендикулярно ему, как и в предыдущих результатах.

Ссылки

• BIGS animation  (англ.) Круговое движение
• Circular Motion  (англ.) — глава из онлайн-учебника

См. также

• Момент импульса
• Уравнения движения
• Математический маятник
• Центростремительная сила
• Сила инерции

Математика кругового движения

Существуют три математические величины, которые будут представлять для нас наибольший интерес при анализе движения объектов по окружности. Этими тремя величинами являются скорость, ускорение и сила. Скорость объекта, движущегося по окружности, определяется следующим уравнением.

Ускорение объекта, движущегося по кругу, можно определить с помощью любого из двух следующих уравнений.

Уравнение справа (выше) получено из уравнения слева заменой выражения для скорости.

Суммарная сила ( F _сеть ), действующая на объект, движущийся по кругу, направлена ​​внутрь. Хотя на объект может действовать более одной силы, векторная сумма всех их должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если она есть), так что внешняя сила уравновешивается, а неуравновешенная сила направлена ​​в центр круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:0003

Уравнения в середине (вверху) и справа (вверху) получаются из уравнения слева заменой выражений для ускорения.

Этот набор уравнений кругового движения можно использовать двумя способами:

• как «рецепт» для решения алгебраических задач для решения неизвестной величины.
• как руководство к размышлению о том, как изменение одной величины повлияет на другую величину.

Эти два способа показаны ниже.

 

Уравнения как руководство к мышлению

Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение для второго закона Ньютона определяет, как ускорение связано с результирующей силой и массой объекта.

Связь, выраженная уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. На самом деле, если бы результирующая сила увеличилась в 2 раза, уравнение предсказало бы, что ускорение увеличилось бы в 2 раза. Точно так же, если бы результирующая сила уменьшилась в 2 раза, уравнение предсказало бы, что ускорение ускорение уменьшилось бы в 2,9 раза.0003

Уравнение второго закона Ньютона также раскрывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0003

Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на другую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Предсказательная способность уравнения усложняется, когда одна из величин, входящих в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее результирующую силу ( F _net ) к скорости ( v ) объекта, движущегося в равномерном круговом движении.

Это уравнение показывает, что результирующая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. Для постоянной массы и радиуса F _сеть пропорциональна скорости ² .

Коэффициент изменения чистой силы равен квадрату коэффициента изменения скорости. Следовательно, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза. А если скорость объекта уменьшится вдвое (уменьшится в 2 раза), необходимая результирующая сила уменьшится в 4 раза.0003

Уравнения как средство решения задач

Приведенные выше математические уравнения движения объектов по окружностям можно использовать для решения задач о движении по окружности, в которых необходимо определить неизвестную величину. Процесс решения задачи о круговом движении очень похож на любую другую задачу на уроках физики. Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующих уравнений, подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.

Пример задачи №1 Автомобиль массой 900 кг, движущийся со скоростью 10 м/с, совершает поворот по окружности радиусом 25,0 м. Определить ускорение и результирующую силу, действующую на автомобиль.

Решение этой задачи начинается с идентификации известной и запрашиваемой информации.

Известная информация: м = 900 кг v = 10,0 м/с R = 25,0 м

Запрашиваемая информация: а = ???? F нетто = ????

Для определения ускорения автомобиля используйте уравнение a = v ² / R. Решение выглядит следующим образом:

а = в ² / р

а = (10,0 м/с) ² / (25,0 м)

а = (100 м ² /с ² ) / (25,0 м)

а = 4 м/с ²

Чтобы определить результирующую силу, действующую на автомобиль, используйте уравнение F _net = m•a. Решение заключается в следующем.

F _нетто = м • а

F _нетто = (900 кг) • (4 м/с ² )

F _нетто = 3600 Н

Пример задачи №2 Полузащитник весом 95 кг делает разворот на футбольном поле. Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. Определить скорость, ускорение и чистую силу, действующую на полузащитника.

Решение этой задачи начинается с идентификации известной и запрашиваемой информации.

Известная информация: м = 95,0 кг R = 12,0 м Пройдено 1/4 окружности за 2,1 с

Запрашиваемая информация: v = ???? а = ???? F нетто = ????

Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d — одна четвертая длины окружности, а время — 2,1 с. Решение выглядит следующим образом:

v = d/t

v = (0,25 • 2 • пи • R) / t

v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)

v = 8,97 м/с

Для определения ускорения полузащитника воспользуемся уравнением a = v ² /R. Решение будет следующим:

a = v ² /R

а = (8,97 м/с) ² / (12,0 м)

а = (80,5 м ² /с ² ) / (12,0 м)

а = 6,71 м/с ²

Чтобы определить результирующую силу, действующую на полузащитника, используйте уравнение F _нетто = м•а. Решение заключается в следующем.

F _нетто = м*а

F _нетто = (95,0 кг)*(6,71 м/с ² )

F _нетто = 637 Н

 

В уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных реальных сценариев движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.

 

Мы хотели бы предложить… Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.

Посетите:  Интерактивное  равномерное круговое движение || Моделирование горизонтального круга

 

Проверьте свое понимание

1. Анна Литикал тренируется дома с демонстрацией центростремительной силы. Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».

 

2. Линкольн Континенталь и Юго делают поворот. Lincoln в четыре раза массивнее Yugo. Если они совершают поворот с одинаковой скоростью, то как соотносятся центростремительные силы, действующие на два автомобиля? Объяснять.

 

3. Cajun Cliffhanger в Great America – это аттракцион, в котором участники выстраиваются вдоль периметра цилиндра и вращаются по кругу с высокой скоростью. Когда цилиндр начинает вращаться очень быстро, пол убирается из-под ног гонщиков. Как влияет удвоение скорости на центростремительную силу? Объяснять.

 

4. Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.

 

Перейти к следующему уроку:

Равномерное движение по окружности с примерами

Ключевые понятия

• Равномерное движение по окружности
• Период времени

Введение:  

В этом занятии вы прочтете о равномерном круговом движении и свяжете радиус круга, образующегося при круговом движении, скорость объекта и период времени.

Объяснение:  

Равномерное круговое движение  

Это движение объекта, движущегося с постоянной скоростью по круговому пути.

1. Может быть равномерным с постоянной скоростью.

2. Может быть неравномерным при изменении скорости вращения.

При равномерном круговом движении скорость или величина скорости постоянны.

Направление вектора скорости непостоянно. Поскольку есть изменение направления, есть ускорение.

Период времени  

Период времени при равномерном круговом движении – это время, необходимое для того, чтобы совершить один полный оборот по окружности, то есть совершить один полный оборот.

Т =

2πrv2πrv

Где r — радиус образованной окружности,

v — скорость движущегося объекта, а

T — период времени одного оборота.

Примеры равномерного кругового движения:  

1. Движение искусственных спутников вокруг Земли.

2. Движение электронов вокруг ядра в атоме.

3. Движение лопастей ветряной мельницы.

д. Движение секундной, минутной и часовой стрелки в наручных часах.

Вопросы и ответы  

Вопрос 1: Перечислите несколько примеров равномерного кругового движения из вашей повседневной жизни.  

Ответ:  

Несколько примеров равномерного кругового движения из повседневной жизни:

• Спутники, вращающиеся вокруг Земли.

• Обращение Земли вокруг Солнца.
• Вождение автомобиля по круговой траектории.
• Гигантские колеса в парке развлечений.

Вопрос 2: За какое время будет двигаться мальчик в карусели, если радиус карусели 20 м и скорость мальчика вокруг карусели составляет 40 м/с.  

Ответ:  

Радиус карусели = 20 м

Скорость мальчика = 40 м/с

Согласно формуле, T =

2πrv2 πrv

= 2 × 3,14 ×

20402040

= 3,14 с

Вопрос 3: Колесо автомобиля имеет радиус 0,34 м и вращается со скоростью 900 оборотов в минуту (об/мин) на балансировочном станке. Определите скорость в условных единицах, с которой движется внешнее колесо автомобиля.  

Ответ:  

Ответы:

900 оборотов за 1 минуту

Итак, 1 оборот за

100

900 06 мин =

100 × 60

= 0,07 с

∴ ∴ 

Период времени = 0,07 с

радиус = 0,34 м 6 = 30,5 м/с

Резюме

• Равномерное круговое движение движение объекта, движущегося с постоянной скоростью по окружности.

  No related posts.